寒区隧道保温设防长度工程实践与研究进展综述

庞小冲，朱小明，穆彦虎，张坤，张力杰，郑波，李凌洁

（1.甘肃省交通规划勘察设计院股份有限公司，甘肃 兰州 730030；2.中国科学院西北生态环境资源研究院冻土工程国家重点实验室，甘肃 兰州 730000；3.中国科学院大学，北京 100049；4.西北民族大学土木工程学院，甘肃 兰州 730124；5.中铁西南科学研究院有限公司，四川 成都 611731）

0 引言

隧道是公路、铁路交通基础设施的重要组成部分，对于提升交通运输效率、服务水平、降低运输成本至关重要，同时对于降低对环境的影响、减少二氧化碳排放具有重要意义［1］。在过去20年里，国内外隧道工程建设发展迅猛。截至2021年，公开统计数据表明中国公路隧道数量和里程达到了2.3万座和2.5万千米，铁路隧道数量和里程达到了1.7万座和2.1万千米［2-3］。尤其近些年来，以川藏铁路、共玉高速为代表的寒区铁路、公路建设快速发展，隧道工程建设向更高海拔和更高纬度地区推进，其面临的环境气象和工程地质条件日益复杂，工程设计和建造难度越来越大。

在广袤的寒区，受严寒气候影响，隧道工程建设面临着一系列严峻的冻融病害挑战。隧道开挖贯通后，洞口段围岩与温度季节变化的外界空气进行热量交换，使得衬砌结构与围岩体经历循环冻融过程，尤其在水分的参与下冻融过程中的水分迁移、冰水相变、冻结膨胀等物理、力学现象可导致隧道洞内挂冰、路面结冰、排水系统失效、衬砌开裂、路面冻胀与融沉等一系列冻害问题［4-5］。已有工程实践表明，中国、美国、俄罗斯、北欧、日本等国家的寒区隧道冻融病害十分普遍，这不仅影响隧道的安全运营，同时增加了后期维修养护成本［6-12］。因此，保温设防是寒区隧道设计与建造的关键和难点。近年来，以太阳能、地热、电能和风能等为热源的主动加热防冻措施发展迅速，但尚未大规模应用于工程实践［13-14］。在防治寒区隧道冻融病害的各种措施中，保温法仍是工程建设中应用最为广泛且有效的一种方法。目前，寒区隧道工程常用的保温材料可分为无机材料和有机材料两种，其中无机保温材料主要有矿渣棉、岩棉、玻璃棉和硅酸铝纤维板，有机保温材料主要有聚苯乙烯、聚乙烯、聚氨酯、聚酚醛等。

在寒区隧道保温设防设计中，保温层的敷设长度和厚度是两个关键参数。就保温层敷设厚度而言，其设计取值相对容易确定，然而保温层的敷设长度确定缺乏统一的依据和简便、可靠的方法，给工程的设计带来了难度和不确定性［15-20］。目前，寒区隧道保温层敷设长度的确定方法主要有工程类比法、经验公式法、理论解析法、数值分析法以及现场实测法，在工程实践中不同隧道所采用的方法不尽相同。寒区隧道保温层敷设长度的确定是一个涉及流体力学、传热学、结构力学、岩土力学等学科的一个复杂问题。同时，由于受到包括隧址区环境气象与地形、地层结构与地下水，以及隧道结构与尺寸等诸多因素的影响，以上方法在应用过程中存在一定的局限性和不确定性。针对同一隧道，不同方法或者不同工程设计人员使用同一方法时也可能造成设计结果的不同。因此，如何科学、合理、简便地确定寒区隧道保温设防长度仍是摆在工程设计和科研人员面前的难题。

针对这一难题，本文首先探讨了现行规范中有关寒区隧道保温设防长度的要求以及目前存在的问题，然后介绍了实际工程设计中常用的经验公式和工程类比法。在此基础上，对保温设防长度相关的寒区隧道温度场理论解析和数值模拟研究进展进行了论述。最后，结合规范发展、经验公式、工程类比法以及寒区隧道温度场研究进展，讨论了寒区隧道工程实践和下一步研究应该关注的几方面问题，包括设计用气象数据的时间尺度、隧址区气象条件与气象台站数据间的差异、保温设防长度确定的依据和取值、隧道进出口的差异性以及多年冻土和季节冻土隧道的区别等问题，以期为寒区隧道保温设防工程设计和后续研究提供参考。

1 规范要求与发展

1.1 铁路规范要求

关于寒区隧道保温设防问题，最初主要参考铁路隧道设计规范中关于保温水沟的设置要求。2001年版《铁路隧道设计规范》［21］中规定，冬季有水的隧道，当最冷月平均气温在-15～-10℃时，宜设置双侧保温水沟；在-25～-15℃时，宜设置中心深埋水沟；低于-25℃时，宜设置防寒泄水洞。2005年版《铁路隧道设计规范》［22］对这一规定进行了相应的修改，规定最冷月平均气温低于-5℃地区冬季有水隧道的冻害地段，宜设置保温水沟、中心埋深水沟或防寒泄水洞等措施。上述两版规范中，并未专门涉及寒区隧道保温设防问题，而是在防水和排水相关条款中提及保温要求。至2016年，再次修订的《铁路隧道设计规范》［23］中将“严寒及寒冷地区隧道”单独成节，明确提出了严寒及寒冷地区隧道应设置保温设防段，明确应当综合考虑隧道的长度、当地最冷月的平均气温和地下水情况、隧道洞内外的气温和风速、风向，以及交通量（包括行车的速度和密度）等因素来确定保温设防的长度，但并未给出具体的确定方法，仅提及在一般情况下新建隧道可参考当地最冷月平均气温，并结合工程类比法参考邻近隧道的设防条件进行确定。在该版规范中，依据最冷月平均气温将隧道气象环境分为三类，即微冷地区（＞-3～2.5℃）、寒冷地区（＞-8～-3℃）和严寒地区（≤-8℃）。可以看出，以上三本铁路规范对寒冷地区的定义越加严格，体现了寒区隧道保温设防的重要性以及这一问题的复杂性。

1.2 公路规范要求

有关寒区公路隧道保温设防，目前我国有《季节冻土地区公路设计与施工技术规范》［24］可供参考。针对季节冻土区隧道保温抗冻，该规范明确指出隧道内气温沿隧道进深方向的变化是决定保温设防长度的关键，但由于现有研究资料较少，实测数据不多且规律性不强，相关数据仍有待收集。该规范针对不同长度的公路隧道，给出了不同隧址区最冷月平均气温条件下无电伴热时的隧道保温设防的长度建议值，如表1所示。可以看出，表中仅涉及隧道长度小于3 000 m工况，对于长度超过3 000 m以上情况未做出明确规定。同时，与铁路隧道规范要求比对，表1中保温设防长度明显较小，而工程实践中实际铺设长度往往大于表中推荐值［25-27］。在该规范中［24］，有关隧道寒冷程度以最冷月平均气温＞-8～0℃划 分 为 冷，＞-15～-8℃划 分 为 寒，将≤-15℃划分为严寒，与2016年版《铁路隧道设计规范》［23］相比，对严寒地区的划分宽松，相应的保温设防要求低。

表1 无电伴热时隧道保温隔热设防长度［24］Table 1 Thermal insulation length of tunnels without electric tracing heat［24］

针对多年冻土区公路隧道，青海省发布了地方标准《多年冻土区公路隧道技术规范》［28］。该地方标准对不同最冷月平均气温条件下排水沟的保温形式进行了规定，选用标准与2001年版《铁路隧道设计规范》［21］基本相同，但把对保温水沟的最冷月平均气温范围由铁路规范中的-15～-10℃进一步提高为-15～-5℃。在对隧道防寒保温设计与施工的表述中，其对保温层厚度的计算方法、设置位置、材料选用等进行了规定，但并未对保温层铺设长度进行明确。

综上，从我国铁路和公路隧道保温设防长度规范的发展历程中不难看出，对于影响或决定隧道保温设防长度的因素目前已有统一的认识，主要包括隧道自身的长度、隧址区的最冷月平均气温（一般采用临近气象台站）和隧道内地下水情况、隧道洞内外的气温和风速、风向以及车流量等，但是由于现有研究资料较少，已获取实测数据不多且规律性不强，目前仍有待现场数据的不断收集和相关研究的深入。值得注意的是，目前相关行业和研究单位在已有工程经验和最新研究进展的基础上，已经在推动一些地方性标准和技术规范的建立，突出了寒区隧道的特殊性并对工程勘察、设计、施工和运维工作进行指导和规范。例如，由四川省市场监督管理局发布的《川西高原公路隧道设计与施工技术规程》［29］，以及交通运输部发布的《寒区公路隧道技术规范》（征求意见稿）。

1.3 国外规范要求

挪威是隧道大国，同时也面临着中高纬度寒区隧道的冻融病害问题。挪威的隧道防冻设防是基于隧址区冻结指数（frost index，单位为h·℃）进行的［30］，这一点与我国公路和铁路隧道多以最冷月平均气温为依据进行设防不同。在冻结指数的选用方面，明确提出应以10年一遇的冻结指数进行保温设防，同时指出隧址区的冻结指数往往大于市政当局给出的冻结指数，因此建议设计用冻结指数应当基于隧址区的实测数据。

在有关隧道内防冻设防长度方面，该规范也明确指出，隧道内的冻结情况不确定性显著。因此，对于长度小于500 m隧道，洞内的保温设防均应按照隧址区10年一遇的冻结状况进行设计。而对于长度大于500 m的隧道，由于隧道工程显著的个体差异性，隧道内的冻结情况必须基于当地的环境气象条件、隧道自身结构、尺寸以及同类隧道的经验单独进行评估，但是同样没有给出具体的评估方法。同时，规范也指出如果可能应测量隧道内的通风情况，这体现了通风情况对隧道内冻结情况的显著影响，包括自然通风、机械通风以及车辆活塞效应等。此外，规范中还提及一些位于气候分水岭上的长大隧道，在进出口段高、低压的影响下其洞内的冻深情况可能与正常情况下有所不同。

2 经验公式确定法

2.1 黑川羲范公式

在寒区隧道保温设防长度确定方面，目前我国应用广泛的是黑川羲范公式［31］。该公式是日本学者黑川羲范在1980年基于日本国内264座铁路隧道洞内气温统计结果而提出，具体为

式中：t为洞口最冷月平均气温（℃）；y为保温段长度（m）。

该公式形式简单，自变量为隧道洞口最冷月平均气温，相对容易获取，因此使用起来较为方便。然而，该项工作是20世纪70—80年代完成，有关该公式中涉及的隧道基本情况、气温的测量方法、设防确定的依据等均不是很清楚。同时，随着寒区隧道洞内气温分布及冻结情况的深入认识，以及保温材料、结构和技术的进步，该公式存在的问题和不足逐渐显现。

测试分类方法的标准通常采用准确率，准确率高，说明分类效果好，但对不平衡数据分类，采用准确率是不合适的，因为错分少数类的样本对整体分类准确率影响不大。因此，本次实验采用基于混淆矩阵(Confusion Matrix)的F-value，该值更能测验分类方法的性能。

2.2 黑川羲范公式的修正

现行《铁路隧道设计规范》［23］中规定，洞内气温高于-5℃时，可不设保温排水沟。因此，有些工程中以洞内气温-5℃位置作为保温段终点，由此确定隧道进出口段的保温设防长度。黑川羲范提出了洞内气温-5℃位置点距离洞口长度的计算公式［31］，具体为

式中：x为洞口计算温度（负温，℃）；y为洞内气温-5℃位置点距离洞口长度（m）。

在应用该公式确定隧道保温设防长度时，一些工程实践中在最冷月平均气温基础上减去10℃来作为洞口计算温度x，以此确保足够的安全系数［32］。部分公路隧道工程实践中，考虑公路隧道尺寸较铁路隧道大，会在此基础上继续乘以一个安全系数，例如15%，去确定公路隧道的保温设防长度。这也真实反映了目前寒区隧道保温设防长度在设计阶段的不确定性。

中铁西南院专家结合《铁路工程技术手册（隧道）》［33］中有关保温水沟设置长度，以黑川羲范公式为基础，并以我国多条隧道的保温设防长度加以对比，提出了隧道洞口段的海拔高度、1月平均气温与隧道洞口段保温段长度的关系表，如表2所示［10］。该经验表格将海拔高度作为隧道保温设防长度确定依据，同时强调若海拔和1月平均气温关系与表中不同时，则以气温为准。通过与黑川羲范经验公式对比，不难看出该表格中的经验值是在其基础上增加了50～100 m。

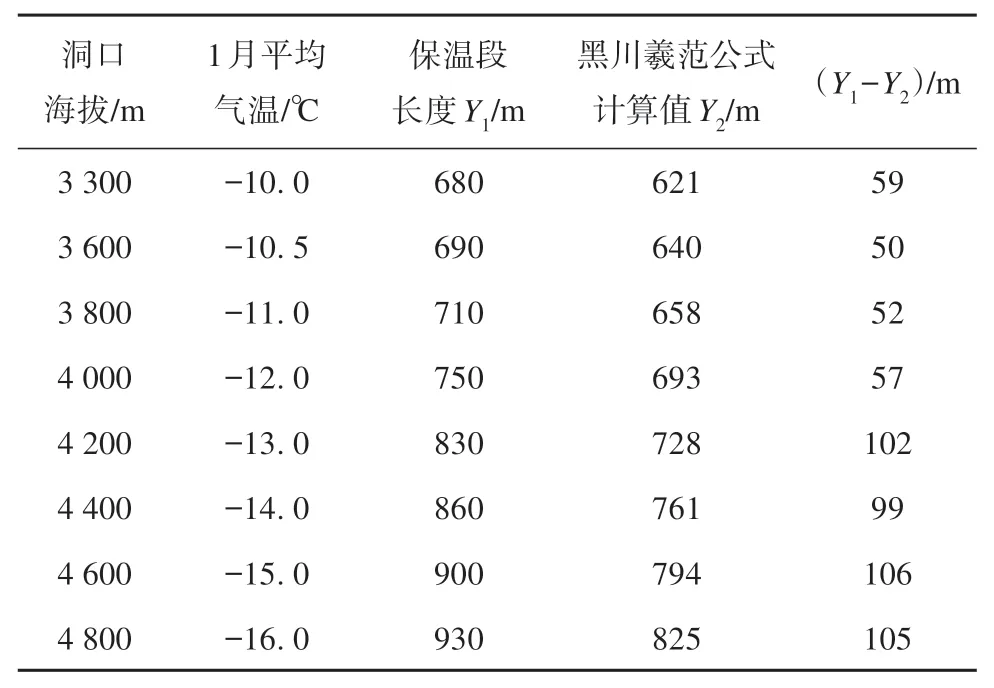
表2 隧道洞口保温段长度经验值［10］Table 2 Empirical value of thermal insulation length at tunnel entrance［10］

2.3 中铁西南院公式

如前所述，以黑川羲范公式为基础，设计人员在大量工程实践和现场监测数据基础上，提出和发展了一些新的经验公式，其中具有代表性的为中铁西南院公式［10］。

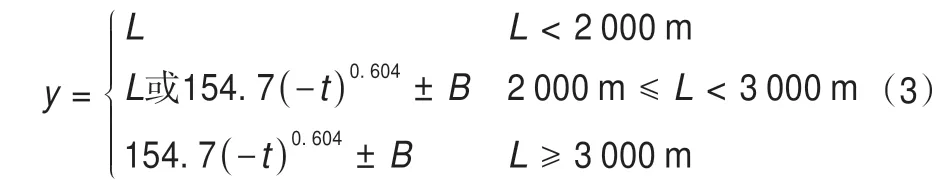
式中：y为保温设防长度（m）；L为隧道长度（m）；t为隧道洞口最冷月平均气温（℃）；B为环境影响量（m）。

可以看出，该公式的修订主要体现在考虑了隧道长度的影响，将隧道长度以2 000 m、3 000 m为界限划分为三个区段。对于长度小于2 000 m隧道，考虑隧道内良好的通风条件建议全隧道通铺保温措施，而对于长度大于3 000 m的隧道则在进出口段布设保温防冻措施。当长度介于两者之间时，则宜结合工程具体条件综合考虑保温防冻措施。该公式是对黑川羲范公式的发展，提出了“环境影响量”这一修正参数，对这一问题的推动具有积极的意义，但该参数如何取值存在一定的不确定性。

在此基础上，郑波等［10］基于对川西高原12座隧道内气温的监测，提出基于洞口气温条件和洞内冷季风速来综合确定隧道保温设防长度，并针对川西高原隧道工程提出了隧道保温设防长度建议值，如表3所示。从表中可以看出，保温设防长度对最冷月平均气温变化不显著，而对最冷月洞口最大风速变化非常敏感，即该建议突出了最冷月洞口最大风速对洞内气温的影响程度。但是，最冷月洞口最大风速值的确定仍然存在一定的难度，多数情况下隧道洞口段地形相对复杂，风速的测量本身存在较大难度，包括观测点位的选择和观测高度（地面上2 m或10 m）［34］。

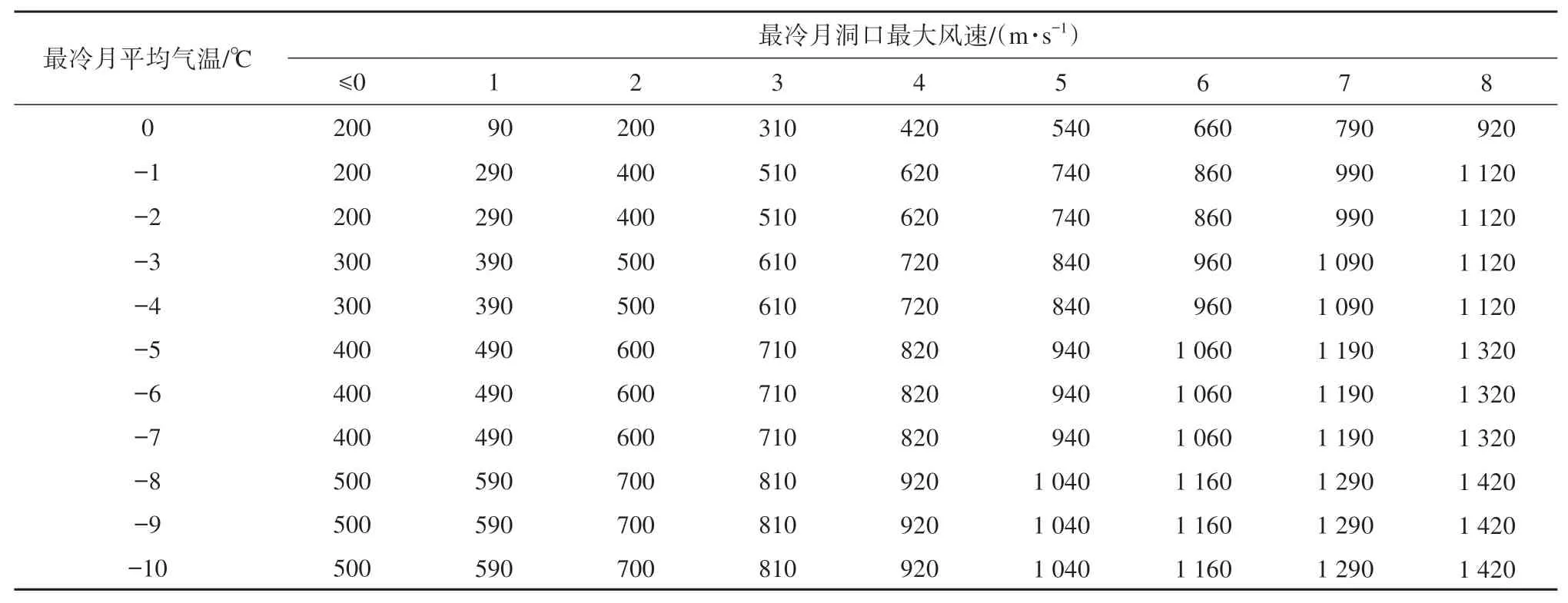
表3 川西高原隧道洞口保温层设防长度建议值［10］（单位：m）Table 3 Suggested thermal insulation lengths for tunnels in Western Sichuan Plateau［10］（unit：m）

式中：y为保温设防长度（m）；t为隧道洞口最冷月平均气温（℃）；f为冷季隧道洞口附近最大风速（m·s-1）。该公式适用于隧道内的自然风以单向通风为主的情况。在迎风洞口端，保温设防长度是在黑川羲范公式的基础上增加了自然风的影响，而在逆风洞口段保温设防长度则给出了一个取值区间，推动了工程实践中对自然风的考虑，具有积极的意义。

3 工程类比确定法

不论是从规范建议还是工程实践的角度，工程类比法同样是目前寒区隧道保温设防长度确定常用的方法，尤其在地理位置临近且环境气象条件相近时，已有工程的保温设防长度往往是新建隧道工程保温设防设计的重要依据。

高焱等［35］对我国156座寒区隧道的冻害调研资料进行了系统的统计分析，并将这156座隧道划分为高纬度隧道（122座）和高海拔隧道（34座）。通过对隧道洞口最冷月平均气温和设防长度的统计回归分析，应用多项式给出了这156座高纬度和高海拔隧道最冷月平均气温和设防长度的拟合公式，如图1所示。

图1 寒区隧道最冷月平均气温和设防长度的统计关系［35］Fig.1 Relationship between mean monthly air temperature of the coldest month and thermal insulation length of tunnels in cold regions［35］：high latitude region（a）and high altitude region（b）

可以看出，工程实际中采用的保温设防长度与洞口最冷月平均气温之间存在着较强的相关性，这反映了目前工程设计中最冷月平均气温仍然是保温设防长度确定最为重要且直接的因素。尽管针对高纬度和高海拔隧道分别提出了不同参数的两个关系式，但两者之间的差别并不大。在最冷月平均气温为-35～-5℃这样一个区间内，两个关系式得到的保温设防长度差值基本在30 m以内，因此从保温设防长度量值确定的角度出发区别高纬度和高海拔寒区隧道意义并不大。

马志富等［27］系统总结了我国寒区隧道的抗防冻设计技术现状，探讨了寒区隧道的设计分区，并结合寒区隧道工程经验、相关规范要求，并考虑进出口气压差的影响，提出了高纬度寒区和高海拔寒区隧道低洞口结构抗冻设防建议长度，如表4所示。从表中不难看出，同样将寒区隧道划分为高纬度和高海拔，同时提出相应的高洞口段的抗冻设防长度可在此基础上适当缩短。有关高、低洞口的提出，反映了隧道进出口气压差的影响。对比高纬度和高海拔寒区设计分区，可以看出即使在最冷月平均气温相近的情况下，高纬度寒区设防段长度相较于高海拔寒区隧道差值在500～1 000 m，量值可观。这一差值较文献［35］统计的工程实际设防长度差值明显。

表4 寒区隧道低洞口结构抗冻设防建议长度［27］Table 4 Suggested lengths for thermal insulation at lower entrance of tunnels in cold regions［27］

叶朝良等［26］基于国内35座季节冻土区隧道洞内实测气温结果，统计分析了隧道纵向影响长度，并给出了保温设防长度建议值。该文献对有关隧道纵向影响长度L的定义为：当隧道气温有高于或等于0℃处时，L指从洞口到隧道内气温为0℃的距离，而当隧道内气温均低于0℃时隧道纵向影响长度，L指从洞口到隧道内气温最高处的距离。然后，对不同隧道相同洞口温度下隧道纵向影响长度的上限进行了拟合，得到了隧道影响长度L与隧道洞口最冷月平均气温t的关系式，如式（5）所示，并将此作为保温设防长度的上限；同时，发现黑川羲范公式恰为保温设防长度的下限。由此，提出取二者平均值并在此基础上向上取整得到建议值，给出了不同洞口温度条件下寒区隧道的保温设防长度，如图2和表5所示。

图2 隧道保温段设置长度上下限［26］Fig.2 Upper and lower limits of thermal insulation length of tunnels in cold regions［26］

值得注意的是，黑川羲范公式［31］是以洞内气温低于-5℃来确定的寒区隧道保温设防长度，而非0℃。因此，由黑川羲范公式得到的保温段设置长度普遍小于实测上限拟合公式计算值，且基本上处于隧道温度纵向影响长度的下限。由此，也引出了寒区隧道保温设防确定依据和标准的问题，有关这一问题在下后续讨论部分论述。从表5提供的保温设防建议值来看，这一量值普遍大于文献［27］的建议值。

表5 保温层设置长度［26］（单位：m）Table 5 Thermal insulation length of tunnels in cold regions［26］（unit：m）

4 理论解析与数值模拟方法

自20世纪90年代以来，国内外学者围绕寒区隧道温度场问题开展了大量研究工作，尤其在工程需求牵引下国内相关研究工作取得了长足的进展，主要体现在理论解析和数值方法方面。近年来，针对寒区隧道温度场，部分学者开展了一些大型模型试验研究［36-40］，丰富了研究手段，并取得了一些研究进展，受限于篇幅这里不再展开论述。

4.1 理论解析法

对于寒区隧道温度场这样一个复杂的非线性耦合传热问题，理论解析法能够给出这一复杂问题中各物理量和时间、空间变量之间明确的数值关系，同时对于工程技术人员而言简便易行且能满足工程精度要求，是获得近似解的一个重要手段［41］。在有关寒区隧道温度场的解析解的研究方面，针对圆形隧道赖远明等认为热量传递是通过热传导进行，通过建立考虑相变潜热的冻结区和未冻区温度场方程，引入摄动技术进行求解，进而得到了已知洞内气温情况下圆形隧道截面温度场的解析解［41］。在此基础上，张耀等［42］考虑洞内气温的季节变化，采用对流换热边界，不考虑围岩体内冰水相变过程，建立了圆形隧道考虑二衬、保温层、初支和围岩4层结构的隧道热传导方程，得到了圆形隧道4层结构的温度场解析解。这些解析解可服务于已知洞内气温情况下隧道保温层厚度的确定。针对同一问题，夏才初等［43］将隧道瞬态传热分解为周期函数边界下的瞬态传热和恒温边界下的稳态传热，利用分离变量和Laplace变化相结合方法，给出了有保温层的寒区隧道径向温度场解析解。上述研究工作，目标在于获得隧道内衬砌结构和围岩体径向的季节冻结或季节融化过程，进而服务于保温层厚度的确定。

相较于隧道径向温度场的求解，隧道轴向即进深方向温度场的求解更加困难，主要体现在隧道内空气流动过程的复杂性。针对这一问题，何春雄等将隧道简化为圆筒，假设气流、温度等关于隧道中心线轴对称，忽略气温的变化对其流速的影响，认为洞内气体以层流为主。对于洞内空气域，其给出了其质量守恒、动量守恒和能量守恒方程；对于围岩体，分别给出了冻结区和融化区的温度场控制方程，考虑了围岩体冻结和融化热物理性质的差异以及冰水相变，进而建立了隧道内空气与围岩对流换热及固体传热的综合模型［44］。随后，何春雄等［45］考虑隧道内的气流为湍流，提出了洞内空气湍流的数学描述方法，即引用Reynolds时均方程方法，将非稳态的控制方程对时间求平均，同时引进脉动动能K方程和耗散率ε方程，利用Boussinesq假设，进而得出紊流黏性系数与脉动动能K和耗散率ε关系的代数方程。夏才初等［43］假定隧道洞内气体的流速不变，基于空气能量守恒给出了隧道洞内空气对流换热传热模型，结合圆形多层介质热传导理论，可在获得隧址区的气象条件、工程条件和地形特征等基本参数的基础上，获得隧道内不同进深位置处空气、保温层、衬砌结构和围岩体随时间变化的温度场解析解。在此基础上，提出了受进口、出口气象条件影响的进口、出口段概念，并以进口气象条件和出口气象条件确定洞内空气年温度振幅相等来划分，最后以初支与围岩体交界面、二衬内表面或二衬与初支交界面温度为0℃为依据来确定隧道保温设防长度［16］。

4.2 数值模拟法

从进出口段保温设防长度角度出发，此处仅对寒区隧道轴向温度场的模拟方法和进展进行论述。寒区隧道轴向温度场模拟的关键在于隧道内空气的流动状态以及流动空气与围岩体之间的对流换热模型的构建。

赖远明等［46-47］、张学富［48］在开展寒区隧道渗流场、温度场、应力场耦合问题非线性分析的基础上，进一步发展和完善了寒区隧道空气与围岩对流换热和围岩热传导耦合问题的三维非线性数值分析方法。在该方法中，假定隧道洞内的气体为层流且不可压缩，通过质量守恒、动量守恒和能量守恒构建气体区域的控制方程，固体传热则与上述隧道径向温度场控制方程相同，然后运用Galerkin法推导给出了详细的有限元计算公式，实现了任意形状隧道洞内空气和围岩温度场的方便计算［48-50］，这一工作推动了寒区隧道围岩温度场的数值求解。谭贤君［51］考虑到隧道结构的横纵比，认为隧道内空气的流动以湍流为主。基于这一认知，对空气湍流控制方程进行了时均化处理，进而得到了时均化的空气连续性方程、运动方程（N-S）方程、能量方程和湿度方程以及K-ρ两方程湍流模型。然后，采用温度壁面函数法，结合已有的洞内流场湍流模型，去求解固体与气体之间的热交换系数。在此基础上，利用数值模拟手段分析了空气温度、湿度、风速对围岩温度场影响规律，结果表明相较于风温和风速，空气湿度对温度场的影响较小［17-18，51］。在此基础上，相关学者开展了包括自然风和列车活塞风作用下寒区隧道轴向温度场的数值模拟研究［52-54］。

值得注意的是，数值模拟方法的优点在于基于构建的理论和计算模型，能够系统量化各个影响因素对隧道洞内温度场的影响规律，进而给出各类工况条件下隧道洞内温度场的分布规律。然而，数值模拟方法中往往包括着一些物理过程的假定或简化，同时所需要的各类参数存在着选取困难和不确定性问题。以外界风对隧道内温度分布的影响为例，模拟过程中风速、风向的时间变化过程往往简化为固定风向和季节性变化风速，由此可能高估了外界风的影响，导致模拟结果与工程实际存在一定的差异，进而影响到保温设防长度的确定。

5 讨论

5.1 隧道保温设计用气象数据的选取

在寒区隧道保温设计中，隧址区环境气象条件至关重要。以设计最常用的最冷月平均气温为例，从工程实践和科学研究角度来看，目前存在着这一量值在选取过程中的时间尺度问题。以国内铁路、公路隧道相关规范和经验公式为例，当前并未明确最冷月平均气温取某一个年际尺度的极值还是平均值［21-24，28］。挪威公路隧道相关规范提出的十年一遇的冻结指数的做法值得借鉴［30］。值得注意的是，在最新发布的《川西高原公路隧道设计与施工技术规程》［29］以及《寒区公路隧道技术规范》（征求意见稿）中已考虑到这一问题并进行了约定，后者明确提出高速公路、一级公路隧道有关气象和标准冻深统计年限不少于近20年，其他等级公路隧道统计年限不少于10年。同时，有关气象数据的来源方面，挪威公路隧道相关规范提出了隧址区冻结情况往往大于市政气象站点提供的数据，进而要求以隧址区的实际观测数据为依据的做法，同样值得借鉴。但是，这一做法在实际操作中存在着一定的难度。在我国，只有国家气象站点具有十年或更长时间尺度的连续气象观测数据，通过隧址区建立气象观测站点进而服务于隧道工程建设目前并不现实。针对这一问题，可结合具体隧道工程，对包括遥感观测数据以及地形、海拔等因素加以考虑，在临近国家气象站点数据的基础上进行相应的修正，以达到设计采用气象数据和标准冻深更加接近隧址区实际气象状况的目的。《川西高原公路隧道设计与施工技术规程》［29］提出针对高海拔长、特长隧道宜在隧址区设立气象观测站（点）并持续收集隧址区气象资料，这一约定值得肯定。长、特长隧道建设周期往往较长，基于工程建设期隧址区气象资料的收集并结合遥感观测数据，实现隧道保温设防的动态优化设计，对于这一问题的解决具有积极的意义。

5.2 寒区隧道保温设防长度的设计依据

寒区隧道保温设防长度的确定目前缺乏统一的依据。从保温设防的目的出发，是为保证隧道排水设施不冻结以避免排水设施失效引发的渗漏水与冻害问题［21-22，30，32］。后来，随着工程实践和科学认知的深入，隧道保温设防逐渐以确保衬砌结构背后的围岩体不冻结为目标。随着对循环冻融作用对建筑材料物理力学性质劣化认识的深入，一些工程实践和研究开始进一步地以（二次）衬砌结构不冻结为隧道保温设防的目标。以黑川羲范公式为例［31］，认为当洞内气温高于-5℃时不会出现冻结情况，因此以洞内气温低于-5℃部分作为保温设防段。后期在一些工程实践和相关研究中，有关保温设防长度的确定有的以初支混凝土表面温度为依据，有的以保温层背面或二衬表面温度为依据，有的则以围岩体表面温度为依据，缺乏统一的依据［16，19-20，26，51］。同时，即使选择同样的依据，如初支混凝土表面温度，但取值也存在不同。设计依据和取值的不统一或者不明确，给工程设计带来了不确定性，而这种不确定性还包括受到上述隧址区气象数据选取不确定的进一步影响。因此，未来针对这一问题需要开展深入的研究工作进而减小工程设计的不确定性。尤其随着隧道衬砌结构、保温层材料和结构的不断发展。以保温层敷设方式为例，目前常用的四种方式包括双层敷设、表层敷设、夹层敷设和离壁式敷设，针对不同的敷设方式和保温设防依据，相应的保温敷设长度势必存在一定的差异，深入量化这些差异对于工程造价的控制和隧道工程的长期安全运营具有积极的意义。因此，针对具体工程，需要从保温设防的目的出发，结合隧道结构以及地下水等工程实际，合理选择隧道保温设防长度的设计依据。

5.3 隧道进出口的差异性

从保温设防角度出发，隧道进口、出口环境气象、海拔、地形地貌等因素的差异可显著影响隧道内的通风情况及温度场空间分布。结合现有工程实际监测的洞内气温轴向分布来看，可将其划分为三类，即关于隧道中心位置对称分布、不对称分布和贯通型分布三类［26，32，55-58］。一般而言，当隧道进口、出口位置包括环境气象、海拔、地形地貌等因素接近且洞内无常年单向风时，隧道内气温沿进深方向呈对称分布。而当隧道进口、出口位置环境气象、海拔、地形地貌等因素差异较大时，隧道洞内往往由于热位差和压差的作用形成单向风，由此一段洞口侵入冷空气的流速大，而另一端流速小，从而使得洞内气温呈现非对称分布特征。第三种情况即洞内气温为贯通型分布往往出现在长度短或埋深浅的隧道内。对于洞内气温对称性分布［图3（a）］，隧道进口、出口是相对的，可以统一考虑其保温设防的设计。而对于洞内气温非对称性分布隧道［图3（b）］，其进口、出口需要单独进行评估和保温设防设计。对于洞内气温贯通型分布隧道［图3（c）］，由于隧道长度往往较小，其保温设计往往采用全隧道贯通统一设计。因此，从保温设防角度洞内气温非对称性分布隧道是目前工程实践和研究的难点，除进出口气象、地形等自然差异外，包括隧道坡度以及通风结构（斜井、机械）及车辆活塞风等因素也能对洞内气温的分布产生一定影响。量化这些影响因素的主次关系，针对不同隧道把握主控因素的同时忽略次要因素，对于工程设计而言可以降低设计参数的确定难度同时保证足够的可靠性。由于这一问题的复杂性，未来仍需要进行深入的现场和理论研究，尤其现场监测数据的积累和丰富至关重要，是理论模型构建和验证的基础。

图3 寒区隧道洞内纵向温度分布类型［56-58］Fig.3 Longitudinal air temperature distribution in tunnels in cold regions［56-58］：symmetrical（a），asymmetric（b）and tunnel-through（c）

5.4 多年冻土区和季节冻土区隧道的差异

“寒区”是一个非常宽泛的概念，从不同学科和不同行业来看，其定义不尽相同，所选取的指标和量值差异显著，最多的定义所选取指标多达10个［59］。从岩土工程角度出发，考虑寒区隧道冻害发育的机理、机制以及防治技术等因素，寒区可以泛指多年冻土区和季节冻土区，这也是目前工程和研究领域广泛接受的。但是，已有工程实践表明，季节冻土区和多年冻土区的工程所面临的问题以及相应的解决思路和技术方法往往是不同的。针对隧道保温设防问题，从洞内空气与围岩体相互作用过程来看，季节冻土区［图4（a）］是冷空气侵入隧道，使得原本融化的围岩体产生季节性的冻结过程，进而引发系列与冻胀有关的工程病害问题，因此保温设防的目的在于针对围岩体和隧道结构的保“融”防“冻”。而对于多年冻土区［图4（b）］隧道，暖空气侵入隧道使得原本常年冻结的围岩体产生季节性的融化，进而引发主要与融沉有关的工程病害问题，因此保温设防的目的在于针对围岩体和隧道结构的保“冻”防“融”。目前，将季节冻土区和多年冻土区隧道统一按照寒区隧道对待，笔者认为不利于针对性的设防思路和技术方法体系的建立。值得注意的是，《寒区公路隧道技术规范》（意见征求稿）已经对该问题进行了讨论，包括寒区的定义以及相关条文中对多年冻土区和季节冻土区区别约定和说明。

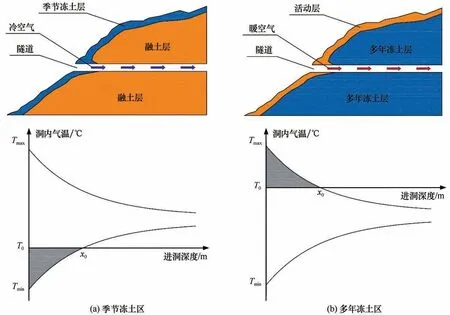
图4 寒区隧道与空气相互作用及保温设防示意图Fig.4 Schematic diagram of interaction between air and tunnel structures in cold regions and determination of thermal insulation length：seasonally frozen ground region（a）and permafrost region（b）（Tmax and Tmin represent annual maximum temperature and annual minimum temperature at the entrance of tunnel，respectively；T0 represents thermal insulation standard temperature；x0 represents thermal insulation length）

6 结论

保温法是目前寒区隧道冻害防治的主要措施，然而针对保温设防长度确定，工程实践和相关研究仍然存在较多的困难和不确定性。针对这一问题，从寒区隧道保温设防长度规范要求、经验公式、工程类比法、理论解析与数值模拟研究进展等进行了系统的总结和分析。主要结论如下：

（1）从现行铁路、公路隧道相关规范来看，提出了寒区隧道保温设防长度需要结合隧址区环境气象、水文地质、隧道结构以及交通量等因素综合确定，且强调了隧址区气象环境监测、洞内气温和风速监测的必要性，但并未明确给出保温设防长度确定方法，使得工程相关设计仍存在着较大的难度和不确定性。

（2）黑川羲范公式是目前寒区隧道保温设防长度设计中广泛参考的经验公式，在该公式基础上工程和科研人员对其提出了一些改进和优化，推动了寒区隧道设计方法和水平的提升。此外，工程类比法仍然是寒区隧道保温设防长度确定中的常用方法。随着认识的深入以及隧道衬砌结构、保温层结构的发展，已有经验公式和工程类比法在工程实际应用中仍存在着一定的不足和局限性。

（3）针对寒区隧道保温设防长度，通过理论解析和数值方法，研究人员提出了一些相应的保温设防长度确定方法。由于这一问题本身属于非线性多因素耦合问题，理论解析和数值方法均存在着一些前提条件和近似假设，且计算过程需要的参数往往较多，增加了其在实际使用过程的复杂性。

（4）针对寒区隧道保温设防未来需要关注和进一步研究的问题，包括设计用气象数据的时间尺度问题、隧址区与临近气象站点环境气象的差异问题、寒区隧道保温设防长度确定的依据及取值问题以及季节冻土与多年冻土区隧道的区别对待等。