城市综合能源网统一前推回代能流计算方法
2022-09-14李卫东胡幸集句荣滨
李卫东,马 俊,胡幸集,句荣滨,李 平
(1. 大连理工大学 电气工程学院,辽宁 大连 116024;2. 国网沈阳供电公司,辽宁 沈阳 110028;3. 国网杭州供电公司,浙江 杭州 310016;4. 国网辽宁省电力有限公司 电力调度控制中心,辽宁 沈阳 110006;5. 国网辽宁省电力有限公司 电力科学研究院,辽宁 沈阳 110006)
0 引言
综合能源系统是能源互联网的载体,对提高能源利用率、实现能源可持续供应意义重大[1-2]。因此,对综合能源系统的分析与求解计算成为当下研究的热点之一,多能流计算对于分析和展示各类系统间的互通关系,指导综合能源系统的建设规划与运行决策均具有重要意义[3]。
目前已有的国内外研究多为针对不同种类系统分别进行建模并考虑耦合部分进行联合的分析计算[4-5]。文献[6-7]分别建立了电-气和电-热综合能源系统模型,并采用顺序求解法进行求解计算。文献[8-9]均采用统一求解法分别对电-气和电-热综合能源系统进行建模和分析。文献[10-11]提出了能源集线器的概念,并将其运用于综合能源系统模型搭建中。文献[12]对综合能源系统能源集线器模型进行了稳态建模,并采用顺序求解法进行求解计算。文献[13]采用牛顿-拉夫逊法对电-气-热综合能源系统混合潮流进行求解计算。综上,尽管国内外学者已经针对综合能源网的能流分析进行了大量的研究,但现有的求解方法多采用解耦后分别计算的方法,不易展示综合能源网中各类子系统间的互通关系,同时解耦后算法的不统一也会导致编程十分复杂;采用统一的牛顿-拉夫逊法进行求解计算对输电系统较为实用[13],然而对于城市配电网而言,由于其支路较多且R/X比值较大,采用牛顿-拉夫逊法具有收敛性较差、求解效率不高等问题。
考虑到城市配电网具有呈单源辐射状的特点,多采用前推回代法进行潮流计算,其具有收敛性好、对初值要求不高等优点。文献[14]对该算法的收敛性与收敛速度进行了研究,并论证了前推回代法与严格的牛顿-拉夫逊法具有相似的收敛速度;文献[15]分析了配电网与输电网间的差异,并基于节点注入电流模型改进前推回代法;文献[16-17]考虑到分布式能源大量接入所带来的PV节点的问题,采用无功修正的方法对算法加以改进。考虑到计算效率及算法的适用性,前推回代法更适用于配电网的潮流计算。然而随着分布式电源的不断接入,现代电力系统中会出现多PV节点的问题,上述算法虽有改进但仍存在迭代次数较多等问题;同时,该算法现阶段仅可用于对电力系统进行潮流计算,需对配热网和配气网进行建模与设计,从而将适用于配电网潮流计算的算法扩展至综合能源系统的能流计算中。
针对以上问题,本文对城市综合能源网统一前推回代能流计算方法展开研究。首先搭建综合能源网中各子系统以及耦合环节的数学模型;然后对于电力系统,通过改进传统算法使其更加适用于实际配电网中可能出现的多PV节点问题,对于热力系统以及天然气系统,分别采用解耦与解环的方式将前推回代法推广至其能流计算中;最后提出综合能源网统一能流计算方法,通过算例验证该算法的正确性与有效性,并进一步展示各子系统的静动态特性以及其对风电消纳的影响。
1 综合能源网模型搭建
1.1 电力系统模型
城市综合能源网中的电力系统模型采用经典交流潮流模型,其各节点的功率计算表达式如下:

式中:Pi和Qi分别为节点i的有功和无功功率;Ui和Uj分别为节点i和节点j电压;Gij和Bij分别为线路ij的电导和电纳;θij为线路ij的功率因数角;n1为节点数。
通过支路流通功率来表示其两端的电压降,即:
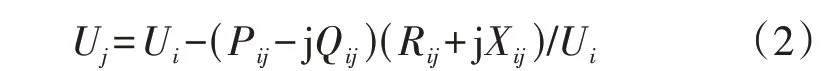
式中:Pij和Qij分别为支路ij传输的有功功率和无功功率;Rij为支路ij的电阻;Xij为支路ij的电抗。
此外,随着分布式电源的不断接入,配电网中的节点类型发生了变化。不同种类的分布式电源并网后对应电力系统节点类型如附录A表A1所示。
1.2 热力系统模型
热力系统模型通常分为水力模型和热力模型。在水力模型中,各管道的流量在各节点处应满足流量连续性方程:流向一个节点的热水的质量流率等于流出该节点的热水与注入该节点的热水质量流率之和,如式(3)所示。
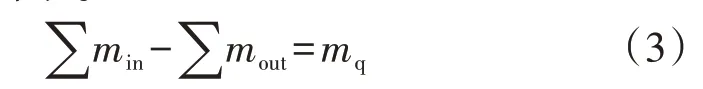
式中:min为流向该节点的各管道中热水的质量流率;mout为从该节点流出的各管道中热水的质量流率;mq为注入该节点的热水的质量流率。
热力模型则是考虑热能、温差以及比热容之间的关系,每个节点消耗的热功率为:

式中:Φ为节点消耗的热功率;Ts为供热温度;To为出口温度;Cp为水的比热容。
热水在管道流动过程中会有热量的损失,沿着水流方向温度逐渐降低,管道末端温度与管道始端温度关系可描述如下:
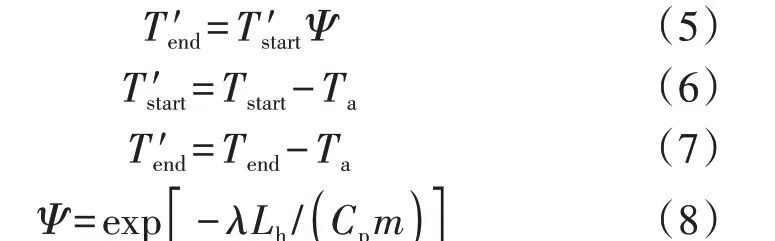
式中:Tend和Tstart分别为管道末端和始端的温度;Ta为环境温度;λ为管道传热系数;Lh为管道长度;m为管道热水的质量流率。
对于辐射形供热网而言,只存在单根管道流向多根管道的节点,节点处热水温度可认为不变。拓扑结构相同但热水流向相反的回热网则存在多根管道中热水汇集于一根管道的节点。由于汇集前各管道温度不一定相同,汇集后的热水温度计算公式为:
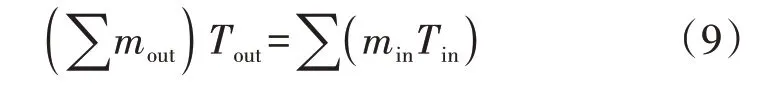
式中:Tout为流向该节点热水的混合温度;Tin为流向该节点的各管道末端温度。
1.3 天然气系统模型
天然气系统管道模型常用天然气稳态气流方程来表达,其描述的是沿管道压力、温度和通过管道流量的关系。考虑到城市配气网的实际运行压力较高,因此选取适用于高压管网的Weymouth 公式描述,具体如下:
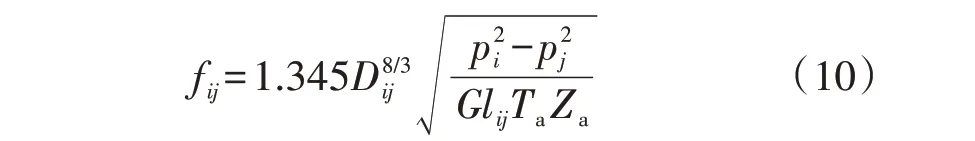
式中:fij为节点i到节点j的管道流量;pi、pj分别为节点i和节点j的气压;Dij为管道ij直径;lij为管道ij长度;Za为平均可压缩系数;G为天然气比重。
将式(10)简单变形可得:

式中:K为管道常数。从式(11)可以看出,不同于电力系统,天然气系统为非线性系统。
考虑到天然气热值与功率的关系,压气机消耗的功率HP可由消耗的气流量计算得到,具体如下:

式中:q为天然气热值,一般取39 kJ/m3;Lcom为压气机消耗的天然气流量。
1.4 耦合环节模型
综合能源系统常见耦合环节有热电联产(CHP)机组、热泵、电锅炉、燃气锅炉等,本文采用含微型燃气轮机的CHP 机组与电锅炉进行耦合。CHP 机组的电功率PCHP、热功率ΦCHP及燃气耗量Fin关系如下:

式中:cm为CHP 机组的热电比;ηe气电转换效率,本文假设其为常数。
电锅炉的能量转换过程满足:

式中:PEB为电锅炉消耗的电功率;ΦEB为电锅炉发出的热功率;ZEB为电热比,设为常数。
2 综合能源网前推回代法能流计算
2.1 电力系统多PV节点处理方法
前推回代潮流算法是对辐射形配电网络进行潮流计算的有效算法,该算法主要分为式(1)、(2)所示的功率回代和电压前推2 个过程,若计算结果不满足收敛条件则再次前推回代直至收敛。然而传统的前推回代法不能很好地处理现代电力系统中大量风电接入所带来的多PV节点问题,因此采用影响因子矩阵法对该算法进行一定的改进。
影响因子矩阵法就是在潮流计算的过程中,先将PV 节点当作普通的PQ 节点来处理,待计算收敛后,将PV节点电压幅值的给定值与计算值之差作为电压不平衡量,再结合影响因子矩阵计算得到PV节点的无功功率补偿量对节点电压进行修正,即:

式中:ΔU为PV 节点电压不平衡向量;ΔQ为PV 节点无功补偿量向量;I为影响因子矩阵,其阶数为网络中PV节点个数。
当一个模型中PV节点个数被确定后,由于网架结构以及线路参数不变,其影响因子矩阵也不会改变,因此当第一次迭代后电压误差不满足精度要求时,仅需重新修正无功功率而不需要重新求取影响因子矩阵。需要注意的是,虽然该算法拟合曲线的拟合度较高,但是无功变化量对影响因子矩阵较为敏感,仍需要尽可能保证拟合精度。因此采用最小二乘法对无功功率在500~1000 kvar附近取点拟合,所得影响因子矩阵精度更高,这可以增加算法的收敛性,减少迭代次数。最小二乘法计算公式如下:

式中:x和y分别为自变量与因变量;k*为拟合斜率。
改进后的算法仅需要计算影响因子矩阵并进行电压修正,求解过程简单且求取影响因子矩阵无需迭代,算法仍会保留传统前推回代法收敛度高、迭代次数少等优点。判断所有的节点电压是否满足收敛条件,若不满足则对注入的无功功率进行修正。PV节点的收敛判定条件为:

上述对传统算法的改进使得前推回代法更加适用于现代城市配电网的实际潮流计算,同时仍保留着其收敛性好、对初值要求不高等优点,在电网潮流计算中优势明显,也为将其应用至综合能源网能流计算中提供了必要性支持。
2.2 基于解耦的热力系统前推回代法
热力系统主要由热源、热负荷及热力网络组成。热力系统节点的相关变量包含热源功率Φ、供热温度Ts、回热温度Tr、出口温度To及热水的质量流率m。根据已知量的不同将热力系统的节点类型划分为平衡节点、普通热源节点、负荷节点与关联节点。
考虑到供热网与回热网拓扑结构完全相同,对热力系统进行解耦,解耦后的供热网具有呈单源辐射状的特点,适用于前推回代法的能流计算。因此可以通过热电比拟的方式将适用于电力系统潮流计算的算法应用于热力系统能流计算中。
电力系统可以抽象视为节点电压驱动,依靠线路电流传输;而在热力系统中可以视为节点供热温度驱动,依靠管道热水质量流率传输。因此可以将电力系统中的节点电压与热力系统中的节点供热温度进行类比,相应地节点电流与管道热水质量流率进行类比。进一步地,在配电网中的功率回代、电压前推、以电流为待求变量的前推回代法,在热管网中可类比为热功率回代、供热温度前推、以热水质量流率为待求变量的热力系统前推回代能流计算方法。
热功率回代过程中,管道热水流量计算如下:

式中:Φki为支路ki的热功率;ΦDi为节点i的热负荷;mki为流过支路ki的热水的质量流率;mDi为节点i的热负荷对应的热流量。
节点i的供热温度前推计算公式为:

式中:Ti为节点i温度;Lki为支路ki的管道长度。
上文给出了解耦后供热网部分的热力系统前推回代能流计算方法。回热网部分与供热网拓扑结构完全相同,但是热水流向相反。因此对应于辐射形供热网,回热网呈汇聚状结构。供热网负荷侧已知的出口温度为回热网各汇聚起点的供热温度,同样采用热功率回代的方式,结合式(9)对汇聚后的热水温度加以计算,最终获得各节点的回热温度。热源节点的总热功率计算公式如下:
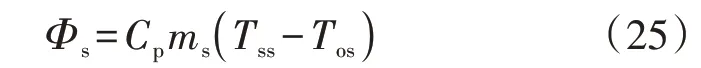
式中:Φs为热源节点的总热功率;ms为系统总热水流量;Tss和Tos分别为热源节点供热温度和热源节点回热温度,其中回热温度可在回热网中求出。
需要注意的是,与电力系统类似,本文在热力系统能流计算中,仅选取一个热功率可变的平衡节点,其余均设为功率已知的普通热源节点。该类节点的热负荷与热功率均为已知,因此本文在后续算例分析中将该类节点的热功率设为数值为负的热负荷进行计算。
2.3 基于补偿气流法的天然气系统能流计算方法
与热力系统类似,采用比拟的思想获得天然气系统前推回代的能流计算方法。天然气系统仅有节点气压以及支路气流量2 个变量,根据已知量不同将天然气系统节点分为平衡节点与负荷节点。
因此,可以采用管道气流量回代、节点气压前推的方式,将前推回代法应用至天然气系统的能流计算中。然而实际配气网存在着环网结构,与热力系统不同的是,该环网结构无法通过解耦的方法处理。对于线性的电力系统,常采用叠加原理处理现代电力系统因故障而导致的配电网中含环的情况[18],但是由于天然气系统并不是线性系统,无法使用线性系统的叠加定理来加以处理。因此需要进一步改进算法,使其可以适用于配气网的能流计算。
基于补偿气流法的天然气系统前推回代法,就是通过解环将环网转换为辐射形网加以计算,并通过线性化补偿气流的方式对解环处气压差值进行补偿,从而实现了含环气网的前推回代法能流计算。以一个简单的含环天然气网络为例给出处理方法,其示意图如图1所示。

图1 简单环网示意图Fig.1 Schematic diagram of simple ring network
图1 是一个简单的3 节点环状网络,在节点3 处解环使其变为节点3 和节点3′。结合式(11)可以计算各相邻节点间的气压平方差,进一步可以获得解环节点处的气压平方差,即:

式中:IC为解环节点间的气流补偿量;I2、I3为节点注入气流量;K12、K23、K13为对应的管道常数;a1、a2、a3为各项系数。
由于二次项系数a1很小,一般为10-10~10-9数量级,因此可以忽略二次项系数,获得开环点气压平方差与补偿气流量之间的线性关系式。由于开环点实际气压是相同的,因此将这个气压差补偿至0 时所对应的气流量即为实际运行线路中的气流量。
附录A 图A1 为下文算例3 中的一条拟合曲线。可以看出忽略二次项后拟合精度很高,算法具有良好的收敛性。对于含有多个环网的天然气系统,补偿气流对各解环点气压均会产生影响。假定在网络中有n个解环节点,则可以绘出n2条类似的曲线,将这些直线的斜率分别作为修正矩阵X(X的阶数为环网个数)的元素,即可获得多环情况下天然气系统前推回代法的修正矩阵。
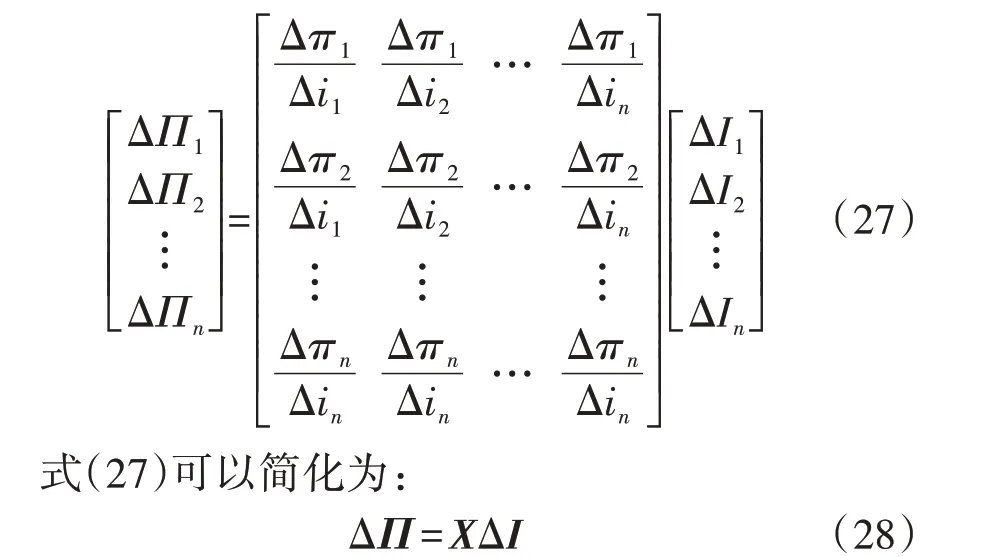
式中:ΔΠ为解环处气压的平方差向量;ΔI为气流补偿量向量;Δπ为解环节点气压平方差;Δi为解环处气流补偿量。
上文给出了基于补偿气流法的天然气系统前推回代能流计算方法,由于天然气系统计算维度较低,且具体的前推与回代过程与热力系统、电力系统相似,因此不再赘述。
2.4 城市综合能源网统一前推回代法
城市综合能源网主要包含电力系统、热力系统、天然气系统以及接入电网的各类分布式电源。上文已分别给出了各类异质系统的模型以及能流计算方法。本文采用比拟的方式,实现了综合能源网能流计算方法上的统一,同时也为后续静特性分析以及综合能源系统的展示与互动研究提供了便利。
除各类系统的能流算法外,耦合环节的加入不仅实现了各类系统在物理层面上的连接,还为多能流间的协调互动提供了“道路”。本文所采用的耦合元件在1.4 节中已详细介绍。综合能源网统一前推回代法能流计算流程图见附录A 图A2。当CHP 机组设置为采用以热定电的工作模式时,具体计算步骤如下:步骤1,初始化各类系统数据,导入各类耦合环节的工作模式;步骤2,解耦热力系统供回热网络,分别采用热力系统前推回代法求解,计算热源节点供热功率;步骤3,将热力系统计算数据导入耦合环节,计算各耦合元件对应的天然气系统与电力系统的负荷或出力;步骤4,更新天然气系统的负荷数据,对解环后的天然气系统采用补偿气流法进行求解,计算气源节点气流量;步骤5,更新电力系统的负荷与出力数据,采用改进前推回代法计算平衡节点电功率;步骤6,计算风电消纳量及各系统网损率。
3 算例分析
3.1 算例1:33节点配电网潮流计算
分布式电源的不断接入使传统的配电网节点类型发生改变。随着配电网中的PV节点不断增多,同时小型自主发电或故障检修可能带来闭环运行等问题,传统的潮流计算方法也应进行改进。算例1在IEEE 33 节点配电网模型的基础上进行修改,其结构如附录B 图B1 所示。考虑分布式电源接入所带来的相关问题,设置节点8、12、15、19、27 为PV 节点,此类节点电压幅值已知,如表1 所示。表中电压幅值为标幺值,后同。除根节点以外的其余节点为PQ 节点,节点31 与节点33 处为闭环设计。其他所需的线路基本参数如附录B 表B1 所示。网络中节点电压幅值的初始值为1 p.u.,相角的初始值为0(和根节点相同),33 节点配电网电压的基准值为12.66 kV。

表1 PV节点无功补偿量Table 1 Reactive power compensation of PV nodes
取误差精度为10-7,经过3 次迭代后程序收敛。各PV 节点处的无功补偿量如表1 所示,2 种潮流算法结果对比如表2 所示。对比表中2 种算法的计算结果,电压最大误差为0.000328%,转换为有名值不足1 mV,相角最大误差为0.0802%。
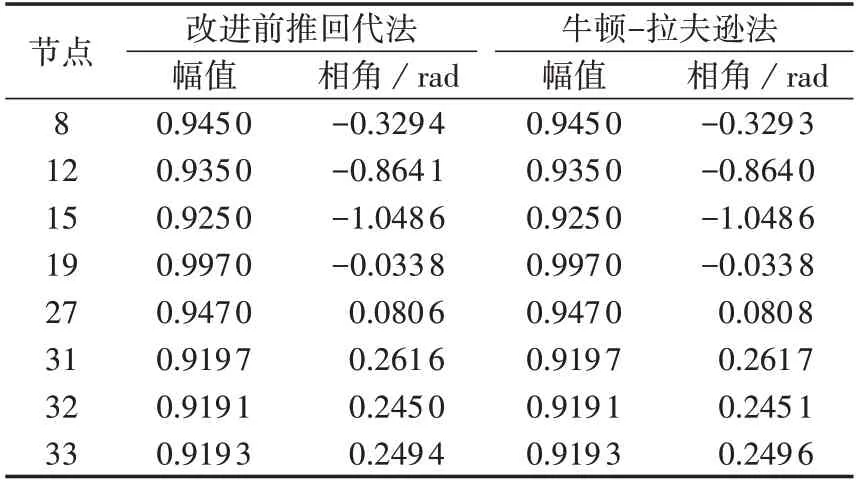
表2 电力系统计算结果对比Table 2 Comparison of calculation results for power system
该算例验证了改进后前推回代法的正确性,具有很好地处理PV 节点与环网的能力。同时算法具有迭代次数少、对初值要求不高的优点,对于牛顿-拉夫逊法收敛性较差的多节点配电网,其仍具有很好的适用性,优势明显。
3.2 算例2:9节点热管网能流计算
由于热网与电网的能流算法是完全比拟的,且电网潮流算法的有效性已在算例1 中得以证明,因此热网能流算法的有效性是可以保证的。故算例2将直接应用上文验证后的前推回代法对9 节点热管网进行能流计算,以验证该方法在热网中的适用性。考虑到热力系统供热网与回热网拓扑结构完全相同,对热管网进行解耦,解耦后的供热网如附录B 图B2所示。
该算例中节点1 为平衡节点,节点2—4 为关联节点,其余节点为负荷节点。该算例中的其他参数如下:热网CHP 机组供热网温度为100 ℃,热负荷回水温度为30 ℃,管道长度为100 m,CHP 机组热电比为1.3,热负荷为0.1 MW。环境温度假定为15 ℃,管道单位长度传热系数近似认为2×10-7MW/(m·℃),此外水的比热容取4.182×10-3MW/(kg·℃)。管道参数如附录B表B2所示。
取误差精度为10-5,进行热力系统前推回代法能流计算。经过3 次迭代后程序收敛。计算结果如表3与附录B图B3所示。

表3 热网能流计算结果Table 3 Energy flow calculation results of heat network
最终计算得热网平衡节点总功率为0.5124 MW。该算例利用热网解耦后呈辐射状的特点,对供热网采用前推回代法进行求解计算,呈汇聚状的回热网利用供热网的质量流率以及热水汇聚公式进行求解计算,从而实现基于前推回代法的热力系统能流计算。这不仅在算法上与电力系统实现统一,同时也具有收敛性好、对初值要求不高等优点。
3.3 算例3:5节点天然气系统能流计算
城市配气网多带有环网结构,非线性的天然气网络无法使用叠加原理加以处理,因此算例3 选取一个含有2 个非独立环状结构的天然气网络,以验证上文所提的补偿气流法对于非线性的含环气网的适用性。网络拓扑结构如附录B 图B4 所示。该算例中平衡节点即节点1 气压为60 bar(1 bar=100 kPa),平均可压缩系数为0.95;天然气温度为288 K,天然气比重为0.589,多变指数取1.175,天然气热值取39 MJ/m3。管道长度及直径等数据如附录B 表B3 所示。在节点3、4 处解环,解环后的新节点设为节点6、7。
分别采用线性化补偿气流法和梯度下降法对上述模型进行求解,选取迭代精度为0.05(气压的平方的初值数量级为103),算例结果见表4。
对比表4 中2 种算法结果,气压最大误差为0.000 336%,气流最大误差为0.001 5%,验证了算法的适用性。当该算法计算精度与梯度下降法相似时,仅需要迭代6 次即可收敛,同时也具有前推回代法潮流计算的诸多优势。

表4 天然气系统计算结果对比Table 4 Comparison of calculation results for natural gas system
3.4 算例4:城市综合能源网单时段能流分析
算例4 以一个实际的区域综合能源网为例,验证本文所提理论方法的有效性。该系统在文献[13]算例的基础上进行改造,电力、热力和天然气子系统通过CHP 机组进行耦合,系统结构如图2 所示,图中EB、HB 和GB 分别表示电力节点、热力节点和天然气节点。
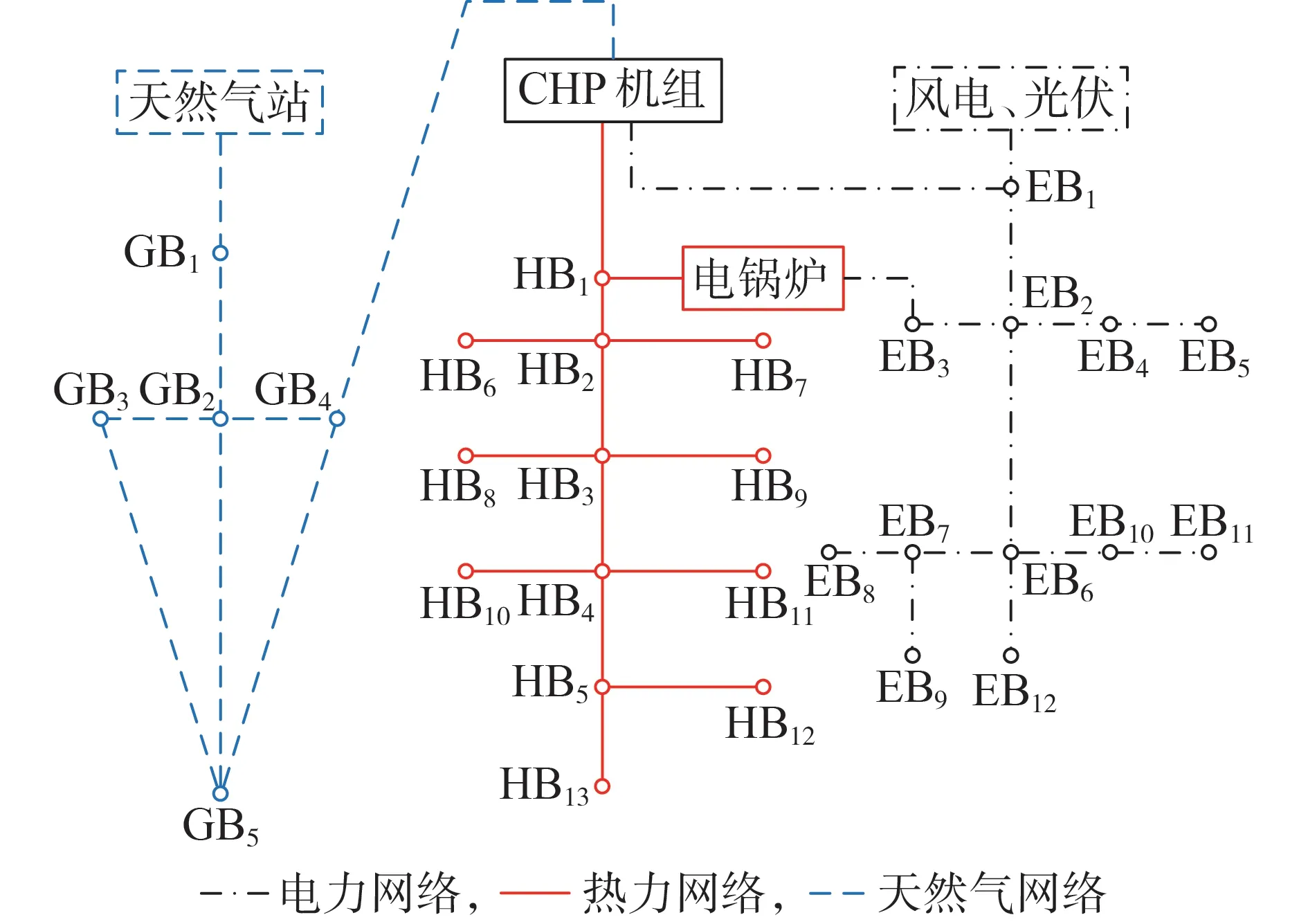
图2 城市综合能源网算例结构图Fig.2 Structure diagram of example for urban IES
图2中电力系统工作于并网模式,节点1连接大电网作为平衡节点,本文假定大电网提供功率不变,剩余有功功率由风电上网补充。节点12、13 为PV节点,节点13通过电锅炉耦合于热网HB1处,电锅炉热电比取1.3,调峰比取0.4。气网、热网与电网通过CHP 机组于GB4、HB1和EB1处耦合,其中CHP 机组工作于以热定电模式,CHP 机组热电比取0.76,燃气轮机组转换效率为0.57。采用不同模型时的计算结果如表5所示。
从表5 中可见,改变热、电负荷或气流量均会对风电消纳等造成影响。对比表中数据,增加热负荷会导致CHP 机组热出力增大,从而增加气网负荷造成气网流量的增加,同时电网出力增大,因此所需风电消纳量降低,反之则会增加风电上网功率。另外,表5 中还展示了改变气流量与电负荷所带来的影响,不再赘述。
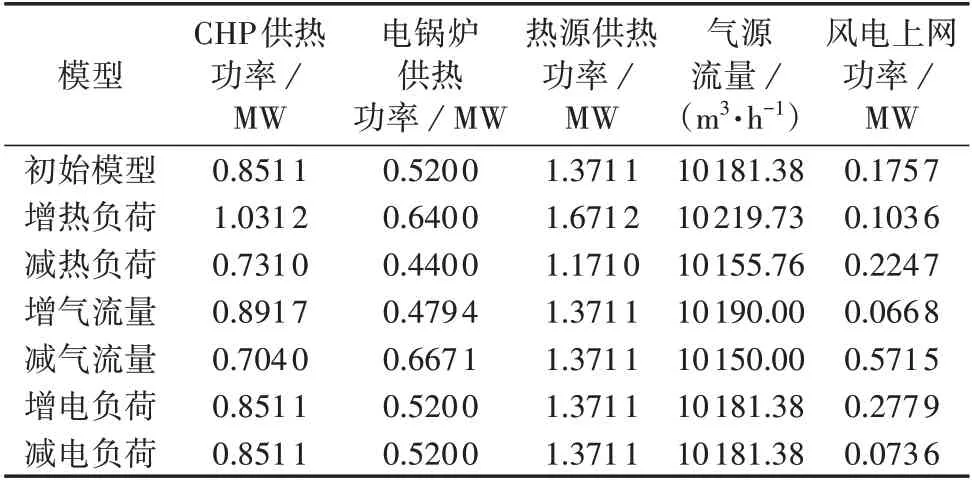
表5 不同模型下的计算结果对比Table 5 Comparison of calculation results under different models
3.5 算例5:城市综合能源网多时段能流分析
上述算例对城市综合能源网单时段断面能流加以计算,并分析其中各类系统间的静态特性及其对风电消纳的影响。在实际综合能源网运行中,由于各节点负荷波动以及各类系统供能出力的变化,各节点的响应同样是一个动态过程。下面本文将通过算例分析展示负荷节点及耦合部分的动态变化。算例系统的总负荷如附录C图C1所示。
在综合能源系统多时段能流计算中,小时级的时间尺度已经具有足够的分析精度[19],因此将负荷侧各时段的时间间隔设为1 h,各时段系统具体负荷值如附录C 表C1—C3 所示。本算例的网架结构以及运行模式与算例4 相同,其中各类系统负荷节点响应均为动态变化,本文仅选取电力系统节点3 处电压(标幺值),热力系统节点2 处的供热温度、回热温度以及天然气系统节点2 处气压值随时间变化的24 h动态数据作为展示,具体如图3和图4所示。选取13—23 时段展示各类耦合环节及系统的出力变化,如图5 所示。综合能源系统中各节点多时段能流计算的其他具体数据如附录C表C4所示。
由图3 与图4 所展示的各系统多时段运行的动态过程可知,节点电压、气压等目标量皆随着系统负荷的变化而变化,但仍需维持在系统的基准值附近波动。系统对负荷变化量及变化率是有一定的限制与要求的,由此保证了系统的安全运行。从图4 可以发现,当确定热力系统网架结构后,同一节点的供热温度与回热温度随负荷变化的趋势是相同的,符合实际热网的运行规律。
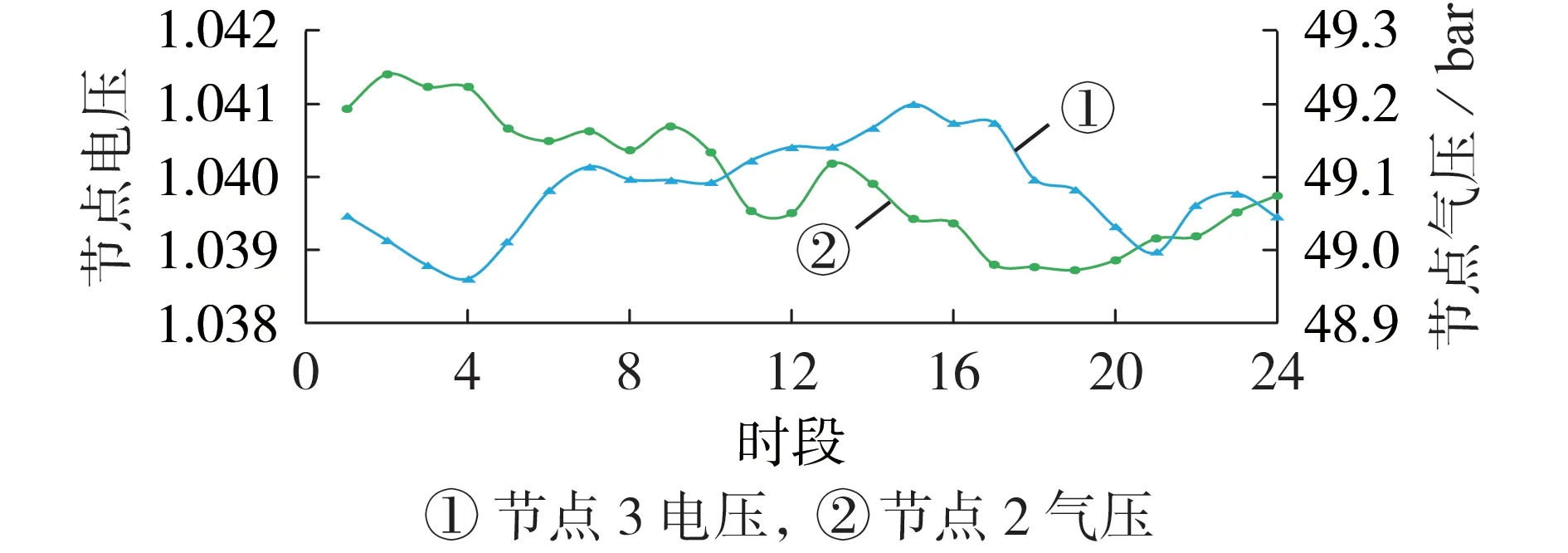
图3 多时段节点电压与气压能流结果Fig.3 Multi-period energy flow results of voltage and gas pressure

图4 多时段节点温度能流结果Fig.4 Multi-period energy flow results of nodal temperature

图5 耦合元件多时段能流结果Fig.5 Multi-period energy flow results of coupling elements
对比图5 所示的电网和热网供能节点发出的功率与附录C 图C1 对应网络的负荷功率,获得对应网络损耗如附录C 表C5 所示。根据表中数据,计算可得电力系统24 h 平均网损为0.518 MW,由系统平均负荷及电锅炉出力可以计算得到电网的网损率约为5.96%,热网的网损率约为1.4%。
4 结论
本文提出了一种城市综合能源网统一前推回代能流计算方法,并通过算例验证了所提算法的正确性。根据算例计算结果,得到以下结论。
1)改进的前推回代法可以很好地处理多PV 节点问题。对于采用牛顿-拉夫逊法时收敛性较差的多节点配电网,其仍具有很好的收敛性。
2)热力能流计算中,采用供热网与回热网解耦分别计算的处理方式,实现了热力系统前推回代法能流计算。同时,考虑热网回水也更加接近于实际配热网的运行情况。
3)天然气能流计算中,所提出的补偿气流法解决了由环网结构所导致的非线性网络无法利用叠加原理进行求解的难题,从而实现了基于前推回代法的配气网能流求解,且所提算法具有很好的收敛性。
4)所提出的统一算法可以更好地展示综合能源系统各子系统间的相互影响。其中单时段仿真可展示各类系统的静态特性,突出各系统间的相互作用及其对风电消纳的影响;多时段仿真则可展示各类系统及耦合元件中能流的动态变化过程。
附录见本刊网络版(http://www.epae.cn)。
