风浪扰动下海上风电机组塔架载荷与输出功率的协同优化控制
2022-09-14唐世泽陶立壮吴晓璇
唐世泽,田 德,王 爽,陶立壮,邓 英,吴晓璇
(华北电力大学 新能源电力系统国家重点实验室,北京 102206)
0 引言
风电机组运行过程中承受着不均匀和间歇性的风、浪等作用,不可避免地增加了结构载荷[1]。随着海上风电领域逐步发展,机组的大型化也导致结构载荷增加。为减小转速波动,大多数现代风电机组采用了叶片桨距致动的控制系统,其中最主要的是变桨控制,即通过调节叶片桨距角实现高于额定风速情况下的风轮转速调节[2-3]。
优化机组载荷是提高机组寿命的重要途径[4]。由于海床土壤环境和机组高度增加,海上风电机组塔架柔性增加,固有频率降低,塔架载荷增加。研究表明调谐质量阻尼器可以降低塔架载荷[5],但需要设计额外的机械结构。更加经济有效的方法是在转速调节的变桨控制系统中附加额外的气动阻尼。文献[6-7]通过经典控制理论方法设计了塔架主动阻尼器,降低了塔架载荷。然而,气动力作用下机组风轮旋转和塔架运动是耦合的[8]。基于单输入单输出经典控制理论的塔架阻尼设计方法不可避免地影响风轮转速调节回路,从而增加机组的输出功率波动。这说明独立设计转速控制和塔架载荷控制必然造成变桨控制器性能降低。
近几年的研究表明基于状态空间模型设计的变桨控制器能够进一步降低塔架载荷。文献[9]通过线性矩阵不等式方法设计了鲁棒变桨控制器,文献[10]设计了线性变参数增益调度变桨控制器,文献[11]设计了自适应变桨控制器,均降低了塔架载荷。同时风浪等外源扰动引起的风电机组塔架低频载荷不可忽略[12],但相关研究相对较少。针对扰动风速对机组稳定运行的影响,文献[13]通过干扰调节方法进一步优化变桨控制器,实现了风扰动抑制。针对波浪载荷的影响,文献[14]提出了基于线性扩张观测器的变桨控制器,能够精确估计波浪并补偿其引起的塔架载荷。但风浪扰动共同作用下风电机组的塔架载荷控制问题值得进一步研究。
另一方面,大部分相关研究侧重于讨论塔架载荷的控制性能,而风电机组在恒转速运行阶段的控制目标是平稳输出功率和抑制塔架载荷,两方面性能指标需要综合设计。因此,本研究从海上风电机组在气动力作用下风轮旋转与塔架运动的耦合特性角度出发,推导并建立了适用于塔架载荷控制的状态空间模型,从而提出了一种基于随机干扰调节控制器SDAC(Stochastic Disturbance Accommodating Controller)的变桨控制策略。该策略旨在协调转速控制和载荷控制,平抑风浪扰动引起的风轮转速和塔架运动波动,保证平稳机组输出功率的同时减小塔架载荷,提高机组运行可靠性。
1 风电机组塔架载荷控制模型
1.1 塔架运动的动力学方程
海上风电机组运行过程中,受到不断变化的风作用,气动力使风轮旋转,通过传动链将机械能转化为电能,风推力也不可避免地造成机组塔架运动。气动力作用下的机组风轮旋转与塔架运动的耦合作用,增加了机组动力学建模的难度。合适的数学模型是大多数先进控制器设计的基础,决定了控制器的性能,因此建立了一种适用于塔架载荷控制的低阶状态空间模型。
相较于气动载荷,水动力载荷对固定式海上风电机组的影响相对较小,且其建模复杂。为清晰描述塔架动力学,将水动力载荷视为风电机组的有界外部扰动。为分析影响风轮旋转与塔架运动低阶特性的主要因素,首先进行如下假设:①塔架在前后方向和侧面方向上对称,即质量、结构阻尼和刚度在2个方向上相同;②塔架的阻尼是线性的;③塔架的扭转运动很小,忽略不计;④机舱重心变化很小,当机组运行时可忽略不计;⑤各叶片的气动性能完全相同。
基于上述假设,用一阶模态将塔架运动近似为前后运动和侧向运动。此时,塔架运动可以表示为式(1)所示的二阶系统。

式中:Je为传动系统的等效转动惯量。
变桨执行器的动力学特性以一阶微分方程近似描述,引入中间变量βis=τ βi(βi为叶片i变桨执行器输出的桨距角,τ为变桨执行器时间常数)便于建立状态空间方程,如式(7)所示。

式中:βc为控制器输出的桨距角。
1.2 塔架运动的控制模型
为了解决变桨控制器设计优化问题,需要推导得到一个合适的状态空间方程。作用在轮毂上的弯矩和力是非线性的,联立式(2)—(5),在运行风速点附近线性化处理得到:

1.3 仿真模型介绍
基于GH Bladed 仿真软件进行仿真,该软件在商用风电机组认证中具有权威性,采用5 MW 三脚架式海上风电机组,机组主要参数见附录A表A1。
该机组模型具有高度非线性,比线性模型复杂得多,因此通过分析对比GH Bladed 模型和推导模型的频域响应特性,验证所提低阶状态空间模型的合理性。在有效风速12、14、16、18、20 m/s 下GH Bladed 模型和推导模型中,桨距角、有效风速到风轮转速、塔架前后位移、塔架侧向位移、塔架前后速度和塔架侧向速度的传递函数频域响应曲线分别见附录A 图A2、A3。可以发现,推导模型在低频区域与GH Bladed 模型具有很高的近似度。由于推导模型的阶次远低于GH Bladed 模型,高频特性存在明显差异,但该频率范围不会出现在风电机组正常运行过程中。尽管推导模型忽略了许多高频细节,但更能体现出风电机组动力学响应的主要特性,设计出的控制器阶次更低。因此推导得到的低阶模型适用于变桨控制器的设计。
2 塔架载荷控制器设计
2.1 传统塔架载荷控制器
传统的塔架载荷控制策略如图1 所示。将塔顶前后向运动速度ẋfa作为控制信号,通过控制力增加气动阻尼,在控制器输出桨距角βc上附加较小的桨距角βadd,影响风轮的气动力Fa[7]。该变桨控制器由比例积分(PI)控制器和阻尼控制器组成。PI控制器参数整定方法参考NREL 5 MW 海上风电机组变桨控制器设计方案[17],阻尼控制器设计参考文献[7]。其中PI控制器的数学模型为:
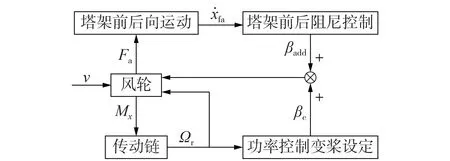
图1 传统的塔架载荷控制策略Fig.1 Traditional tower load control strategy

式中:参数ξc=0.3。
由式(10)可知,气动力作用下风轮转速变化和塔架前后、侧向运动存在耦合,耦合运动不仅与桨距角有关,还受到风浪扰动的影响。因此,使用2 个独立回路方程分别描述转速控制和塔架载荷控制的表示方法并不完善。另一方面,由于海上风电机组体现出的固有低频特性,为了避免在运行过程中激发塔架振动模态,转速控制回路的带宽不能高于塔架载荷控制回路的一阶固有频率,以提高机组对功率波动的平抑能力。
2.2 SDAC变桨器设计
为了解决传统控制策略的矛盾,基于状态空间方程,从多目标优化的角度出发,利用线性二次型调节器LQR(Linear Quadratic Regulator)控制方法,综合设计转速控制和载荷控制,提出了基于SDAC 的变桨控制器设计方案。
式(10)所示方程中包含了变桨执行器的动态特性,当设计基于SDAC 的变桨控制器时,如果机组系统方程同时包含变桨控制输入和风速扰动输入矩阵,那么变桨控制器扰动抑制增益将恒为0,即机组在运行过程中,变桨控制器不对风速扰动产生任何动作。另一方面,当机组处于稳定状态时,控制器补偿风速扰动会导致变桨执行器状态变量一定不为0,尽管动态调节变桨控制器的扰动抑制增益可以使机组保持期望的响应性能,但是这也使控制器的设计过程变得复杂。而未考虑变桨执行器的动态特性时,所设计的SDAC 反馈控制律不会产生任何稳态误差。因此,在设计SDAC 反馈控制律时忽略变桨执行器的动态特性。恒转速工况下电磁转矩Tg保持恒定,即δTg=0,在输入变量中可以省略。综上所述,将风轮转速、塔架前后和侧向运动速度作为输出变量,在式(10)的基础上可得新的状态空间方程,如式(16)所示。

式中:xd为扰动的状态变量;w~(0,W)表示均值为0、功率谱密度为W的高斯白噪声;δε为一个各元素值很小的行向量,表示机组状态变量和扰动状态变量的耦合分量;Ad和Cd为随机扰动模型参数。令Ad=0,Cd=1,所得模型将风浪扰动描述为阶跃分量和随机分量的叠加。其中阶跃分量表示风速扰动,随机分量表示波浪扰动。联立式(16)、(17)可得增广的机组状态空间方程为:

由此可知,变桨控制器增益随矩阵P中元素值的增大而增大,而矩阵Q、R决定了矩阵P的元素值。进而,在设计变桨控制器时,通过调节矩阵Q、R各元素的相对大小,平衡风轮转速、塔架运动等状态变量的变化量和变桨执行器的动作量。矩阵Q的元素相对较大时,状态变量的变化量减小,但变桨执行器的动作量增大,受到实际变桨系统的限制,变桨执行器不一定能满足过于快速的控制指令需求。因此,变桨控制器的性能受矩阵Q、R的影响。值得注意的是,为了确保变桨控制器对风浪扰动的抑制能力,需要反复优化W的取值。设R为单位阵,通过调试,确定正定矩阵Q=diag{25,0.5,110,0.5,7.5,100},进而通过求解黎卡提方程计算出不同风速下的变桨控制器增益,得到变增益的变桨控制器,应用于强非线性风电机组系统。
设图1 所示传统的塔架载荷控制器为基准(Baseline)控制器,将其与所提SDAC进行对比,所得海上风电机组闭环系统的频域响应特性的对比结果如图2 所示。由图可知,该海上风电机组塔架的一阶侧向模态角频率为2.998 9 rad/s(0.477 2 Hz),此模态阻尼较低。所设计的SDAC 能在该角频率处提供足够的阻尼,提高机组运行过程中塔架运动的稳定性。Baseline 控制器同样对塔架的振动提供了足够的阻尼,但其带宽小于SDAC的带宽。
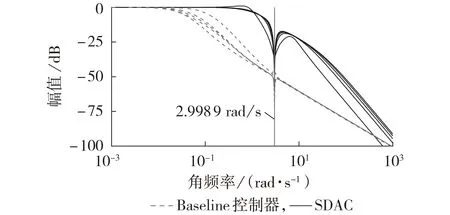
图2 海上风电机组闭环系统频域响应特性Fig.2 Frequency domain response characteristics of closed-loop system of offshore wind turbine
2.3 基于Kalman滤波的状态观测器设计
除了转速和塔架运动速度,状态空间方程中的其他变量均无法直接测量,且受过程噪声w和测量噪声的影响,考虑构造Kalman 滤波器估计系统状态变量。Kalman增益KF为:
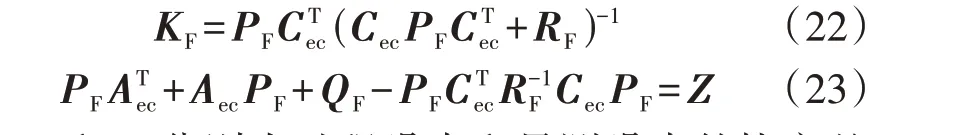
式中:QF和RF分别为过程噪声和量测噪声的协方差矩阵。对于状态估计器,其带宽需要大于控制器带宽,以保证对状态信息估计的准确性,但是过大的状态估计器带宽可能导致整个闭环系统不稳定,因此应当选择合适的Kalman 增益,以平衡估计器和SDAC 的性能。设过程噪声和量测噪声的协方差矩阵分别为QF=diag{0.01,0.01,0.01,0.01,0.01,0.011},RF=diag{1.016 6×10-10,8.132 8×10-6,8.132 8×10-6},根据式(22)计算出不同风速下状态空间方程对应的正定矩阵PF,从而得到Kalman增益KF。
综上,基于SDAC 的变桨控制策略如图3 所示。Kalman 滤波器利用桨距角和风轮转速、塔架运动速度的量测信号估计出状态变量和扰动风速,同时将波浪扰动视为过程噪声进行滤波。Söffker扰动模型通过增广状态空间方程的形式处理风浪扰动信息并输入状态反馈控制中。基于多目标优化的LQR 通过状态反馈控制输出桨距角信号,使机组响应趋近于运行的平衡点。基于SDAC 的变桨控制器能够优化机组在风浪扰动下的响应特性,协调输出功率控制和塔架载荷控制。
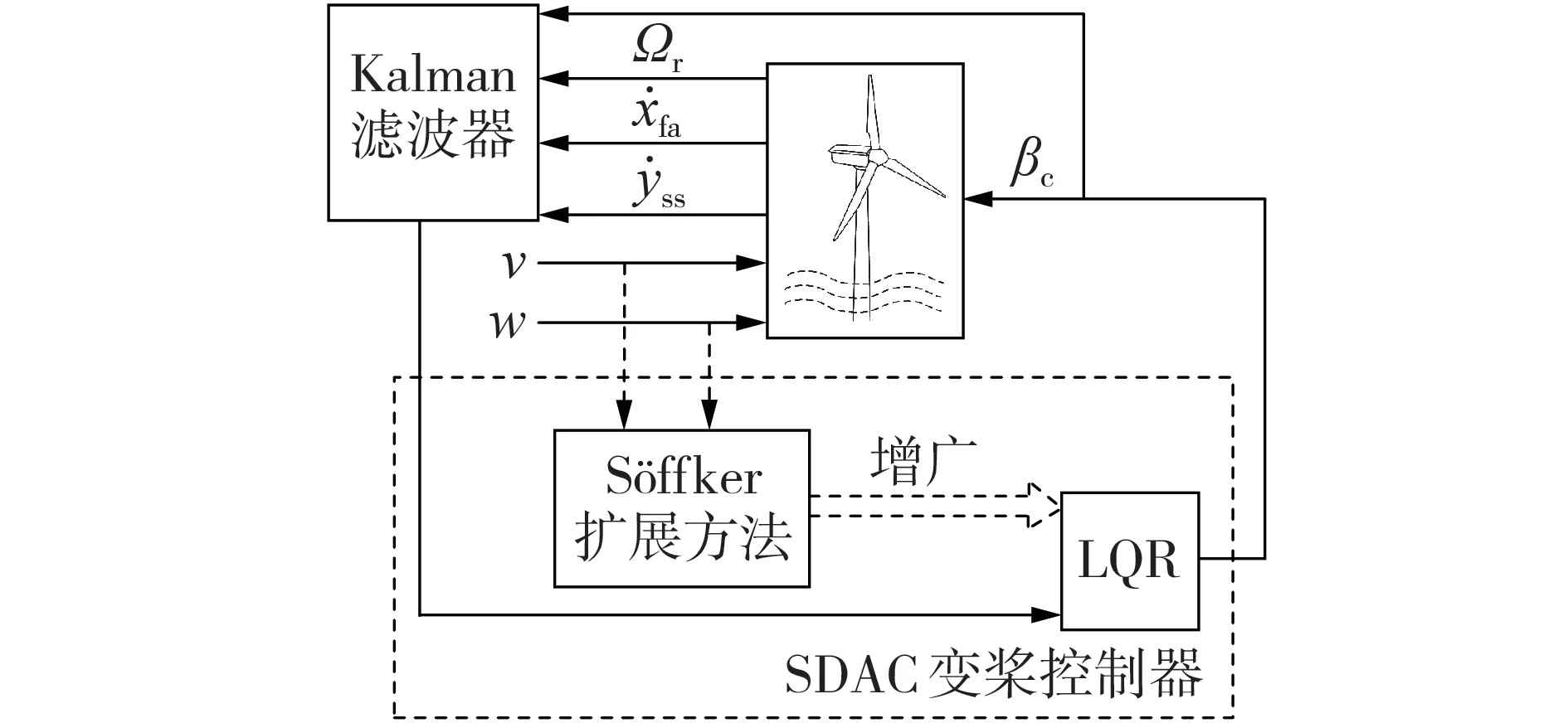
图3 基于SDAC的变桨控制策略Fig.3 Pitch control strategy based on SDAC
3 仿真分析
3.1 湍流风下基于SDAC的变桨控制器性能分析
遵循IEC61400-3 标准[20],在湍流风下仿真,以分析采用基于SDAC 的变桨控制器海上风电机组的闭环响应特性。控制器均通过C++代码以动态链接库的形式集成到GH Bladed 软件中。风电机组转矩控制器的设计方法参考文献[17]。仿真中平均风速为18 m/s,湍流强度为16.9%;以P-M 谱模拟波浪,决定波浪的2 个参数分别为有义波高和峰谱周期,有义波高反映波浪的幅值,峰谱周期反映波浪的频率,设有义波高Hs=6 m,峰谱周期fp=8 s;仿真时间为100 s。仿真结果中选取塔架弯矩位置为塔架顶部,H=78 m,仿真结果如图4所示。
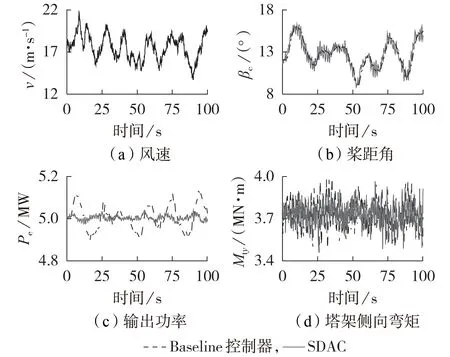
图4 18 m/s湍流风下控制器性能对比Fig.4 Performance comparison of controllers under 18 m/s turbulent wind
从图4(c)可以看出,SDAC 可以平抑输出功率Pe波动,采用Baseline 控制器和SDAC 后机组输出功率标准差分别为0.057 8、0.011 8 MW。图4(b)中的桨距角波形表明,所提控制器通过及时调整桨距角,能够更快地对外部扰动做出反应以应对机组动态波动。Baseline 控制器和SDAC 的变桨速率标准差分别为0.43(°)/s 和1.79(°)/s。尽管SDAC 增加了变桨执行器的动作量,但变桨过程中未出现速率饱和,在设计允许范围内。这表明所提控制器虽然对变桨伺服系统提出了更高的要求,但是具有稳定输出功率的动态波动和降低塔架载荷的功能。由式(1)可知,塔架前后弯矩Mtx主要通过转矩控制调节,在基于SDAC 的变桨控制器下塔架前后弯矩基本无变化,因此不展开讨论。进一步分析SDAC 的塔架载荷控制能力,将塔架弯矩进行频域变换,计算得到塔架侧向弯矩Mty功率谱密度PSD(Power Spectrum Density),采用Baseline 控制器和SDAC 后在一阶模态频率处出现的塔架侧向弯矩PSD 峰值分别为1.30×1011、2.30×1010N·m2·s。可以看出SDAC 能够削弱塔架一阶模态下功率谱密度的峰值,这说明相较于Baseline 控制器,SDAC 在塔架运动方程一阶模态处的共振频率下可提供了更大的阻尼。
为了验证SDAC 在风电机组控制系统集成后的总体性能,在额定风速12 m/s 附近设计仿真模拟。仿真中,平均风速为12 m/s,湍流强度为16.9%,保持波浪条件不变,仿真时间为100 s,仿真结果如附录A 图A4 所示。由图可知,在额定风速以下,转矩控制器保证最大功率输出,桨距角保持最小桨距角,2 种控制策略响应一致。当风速变化到额定风速以上,Baseline 控制器和SDAC 开始动作的时间相同,证明了SDAC 与Baseline 控制器兼容性良好,能够在不影响其他性能的同时,在额定风速以上实现协调优化输出功率与塔架载荷。
进一步研究恒转速运行工况下SDAC 的控制性能,分析不同风况作用下风电机组的疲劳特性。遵循IEC61400-3 标准的DLC1.2 工况,在平均风速为[12,20]m/s 湍流风下,设置机组偏航误差为-8°、0°、8°,仿真时间均为600 s,分别计算机组的输出功率时间序列的标准差和塔架损伤等效载荷DEL(Damage Equivalent Loads),结果如图5所示。由于风速具有随机性,不同风速下塔架DEL 优化效果稍有差异。
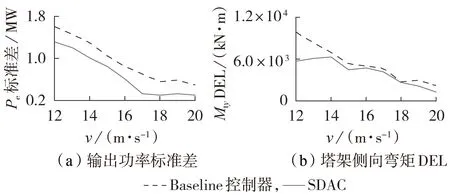
图5 风扰动下控制器性能对比Fig.5 Performance comparison of controllers under wind disturbance
一方面,越接近额定风速,控制器之间的切换越频繁,输出功率和塔架载荷波动越大;另一方面,根据IEC61400-3 标准,平均风速越高,设置的湍流强度越低,机组响应波动越平稳。因此输出功率标准差和塔架侧向弯矩DEL 随风速增大均呈现单调递减规律。根据图5(a)、(b),相较于Baseline 控制器,采用SDAC 时功率波动降低了39.16%,风电机组塔架顶端侧向弯矩DEL 平均降低了12.34%。这进一步证明了SDAC 能够有效降低风电机组在恒转速运行工况下的塔架载荷,实现了输出功率和塔架载荷的协同优化。
3.2 波浪扰动下基于SDAC的变桨控制器性能分析
设平均风速为18 m/s,湍流强度为16.9%,保持有义波高Hs=6 m 不变,峰谱周期fp=2.096 s,此时波浪扰动会激发塔架振动,2 种控制器参与下的仿真结果如图6所示。根据图6(a),采用Baseline控制器和SDAC 后机组输出功率标准差分别为0.058 0、0.011 8 MW,与图4(c)对比发现,波浪载荷增加后Baseline 控制器下输出功率波动,但SDAC 能够保证输出功率波动基本不变,这是因为输出功率稳定性的提升是通过增加变桨控制器的动作量实现的。根据图6(b),采用Baseline控制器和SDAC 后的变桨速率标准差分别为0.45(°)/s 和1.98(°)/s,相较于图4(b)均有所增加。
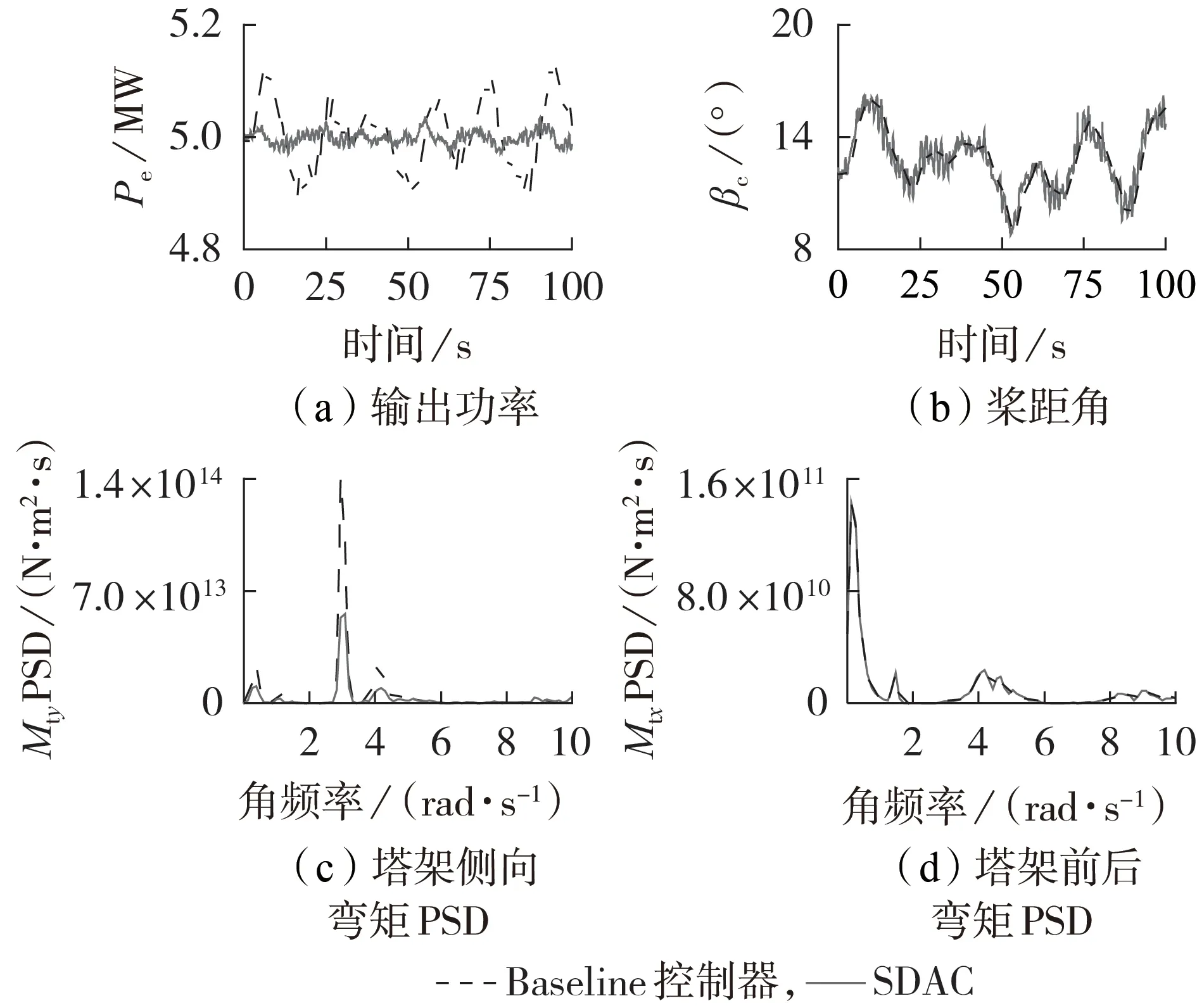
图6 波浪扰动下控制器性能对比Fig.6 Performance comparison of controllers under wave disturbance
从时域很难看出所提控制器的降载效果,因此通过计算得到塔架侧向、前后弯矩PSD,分别如图6(c)、(d)所示。采用Baseline 控制器和SDAC 后在一阶模态频率处出现的塔架侧向弯矩PSD峰值分别为1.41×1011、5.32×1010N·m2·s,这说明当波浪载荷增加,SDAC 在稳定输出功率的同时,仍能保证机组塔架载荷处于较低的水平。不同于3.1节,波浪同时作用塔架前后和侧向2 个方向,此时塔架前后弯矩导致的载荷也需要验证。采用Baseline 控制器和SDAC 后,塔架前后弯矩PSD 峰值出现在0 附近,分别为1.41×1013、1.35×1013N·m2·s,进一步说明了SDAC可以抑制塔架前后弯矩波动。
下面分别分析有义波高和峰谱周期对机组响应特性的影响,进一步研究波浪扰动下基于SDAC 的变桨控制器的响应特性。在600 s 的时间内进行2组仿真:①保持峰谱周期fp不变,有义波高Hs分别设置为0、2、4、6、8 m;②保持有义波高Hs不变,峰谱周期fp分别设置为0、2、4、6、8 Hz。通过仿真计算得到风电机组输出功率的标准差和塔架弯矩的损伤等效载荷,结果如附录A表A2、A3所示。可以看出,采用SDAC 后风电机组输出功率比采用Baseline 控制器时更稳定,塔架疲劳载荷的抑制效果更好,其能够降低塔架前后和侧向疲劳载荷。当波浪的有义波高和峰谱周期发生变化时,SDAC 能够抑制波浪扰动,因此不同波浪扰动下机组输出功率波动和塔架疲劳载荷水平趋于一致。
4 结论
针对海上风电机组的塔架载荷控制问题,设计了含LQR 的基于SDAC 的变桨控制器,其能在稳定输出功率的同时降低塔架载荷。本文的主要工作如下:
1)建立了适合的线性时不变状态空间方程,基于SDAC,利用LQR控制策略改进变桨控制器;
2)通过状态反馈的形式抑制风浪波动造成的功率波动和塔架载荷,提高了控制系统的稳定性,增强了系统的动态响应能力;
3)与Baseline 控制器进行对比,结果表明所提方法能够在风浪扰动下稳定功率输出,同时进一步降低塔架载荷,提高机组运行的稳定性。
附录见本刊网络版(http://www.epae.cn)。
