基于DAB的ISOP型蓄电池测试电源控制策略

施永， 张震， 陈忠， 彭凯

(1.合肥工业大学 光伏系统教育部工程研究中心，安徽 合肥 230009； 2.国网安徽省电力有限公司电力科学研究院，安徽 合肥 230601； 3.合肥科威尔电源系统股份有限公司，安徽 合肥 230088)

0 引 言

蓄电池测试即通过测试电源对蓄电池进行循环充放电，检验蓄电池的容量。目前市场上的测试电源均采用充放电路分开的设计，例如文献[1]充电时，电路采用单相整流加Buck的拓扑结构，Buck电路输出接被测电池组进行充电；放电时，电路采用Boost电路，输出接能耗负载直接将电池电量消耗掉。由于Buck或Boost电路升压比有限，单相整流需要通过工频变压器接入电网，同时，充放电路分开致使测试电源体积大、质量大。文献[2]所述电源采用单相整流后经半桥DC/DC电路输出直流母线电压，由于半桥DC/DC电路采用高频变压器，大大减小体积，直流母线后接双向Buck Boost电路，令充放电电路集成在一起。但在放电时，不能向电网回馈能量，全部通过负载消耗掉，造成电能的浪费，而且测试电流小。为了减小装置体积，实现测试过程能量可回馈，可以考虑采用一种以双向隔离式DC-DC/DC转换器为基础模块，输入串联输出并联型双有源桥变换器作为测试电源DC/DC级，其功率范围大，能大大提高测试电流，文献[3-4]表明大电流能减小蓄电池测试周期。同时输入串联输出并联双有源桥(input-series-output-parallel dual active bridge，ISOP-DAB)变换器可以适用于测试电源的高升压比，避免工频变压器造成电源体积大、质量大。

测试电源需要根据特定的充放电方式对输出进行控制。通常是以先恒流、后恒压相结合的分段充电，以防止在一直恒流充电电池端电压过高而导致极板击穿短路。蓄电池放电时以恒定电流输出。同时，ISOP-DAB变换器均衡控制方法有两种：一是通过硬件电路自校正特性自然均压或均流，二是通过加入相应的控制环路来完成均衡控制。文献[5-6]所述ISOP-DAB变换器应用共同占空比控制，通过硬件电路自校正特性实现均衡控制。其中文献[5]结果表明，当各个模块的电路参数相差很大时，不能有效进行均衡控制。文献[7-8]介绍了ISOP-DAB变流器的典型解耦控制方案，该方案由一个公用的输出电压控制环和一个独立的输入电压控制环组成，实现输出电压控制回路解耦，从而达到平衡控制的目的。这种方法能很好地解决由于各电路参数的不同而引起的电压、电流不平衡问题，但是模块化程度较低。文献[9-10]进一步给出了离散下垂控制方案，将各模块的输入电压和输出电流进行反馈，从而使各模块的输出电流达到平衡。此方法较为简单，但需根据充电组合方式对电源的ISOP-DAB变换器的控制做相应改进。所以，本文提出一种以双有源桥电路作为基本模块的输入串联、输出并联型测试电源，并在充电的不同阶段提出ISOP-DAB变换器的恒流控制和下垂限压控制策略。控制策略实现了ISOP-DAB变换器的输入均压、输出均流控制要求兼顾实现分段充电方式。在充电前期以一定充电电流进行充电，当电池上的电压到达一定的数值时，转换成限压充电。

首先，介绍测试电源电路结构，并分析双有源桥(dual active bridge , DAB)变换器的工作原理，提出针对文中所述ISOP-DAB变换器充电时的恒流控制和下垂限压控制。然后，详细地分析ISOP-DAB变换器的小信号电路，建立相应等效模型。最后，搭建以DAB变换器为基本功率单元的二单元ISOP-DAB变换器仿真模型，验证所提控制策略的有效性。

1 ISOP-DAB型蓄电池测试电源

测试电源主电路结构如图1所示，该测试电源采用模块化结构，交流侧采用220 V单相交流电供电，通过单相整流变换器模块将直流母线电压控制为Uin。DC/DC级采用模块化ISOP-DAB变换器结构。按照测试电池电压等级不同的需求，设计不同标准的ISOP-DAB变换器。同时，可以将多个ISOP-DAB变换器接在母线电压上同时为多个电池进行充放电测试，将电池分为充电组和放电组，放电组放出的电能可以经过直流母线，直接供给充电组电池，多余部分回馈电网，不足的电能由电网补充，实现能量半封闭式测试。

图1 测试电源主电路结构Fig.1 Main circuit structure of the test power supply

第i个DAB变换器拓扑结构如图2所示。图2中：Si1～Si8表示ISOP-DAB变换器的第i个DAB模块的功率开关器件, H桥电路中对角线上对称的开关管(如Si1和Si4)方波驱动信号一致，而同一桥臂的开关(如Si1和Si2)互补通断；np、ns表示模块中高频变压器一次侧和二次侧绕组匝数；Cii为输入侧电容，Coi为输出侧电容；Li为能量转移电感；uai和ubi分别表示一次侧和二次侧的交流方波电压；Uini和Ubat为输入侧电压和输出侧电压，iLi为流过两个H桥之间能量转移电感Li的电流，Ioi为输出侧电流。DAB变换器主要采用单移相(single phase shift，SPS)调制方法，SPS调制单开关周期内一次侧交流电压、二次侧折合交流电压和一次侧电感电流波形[11]以及第i个DAB变换器在SPS调制下的理论波形如图3所示。

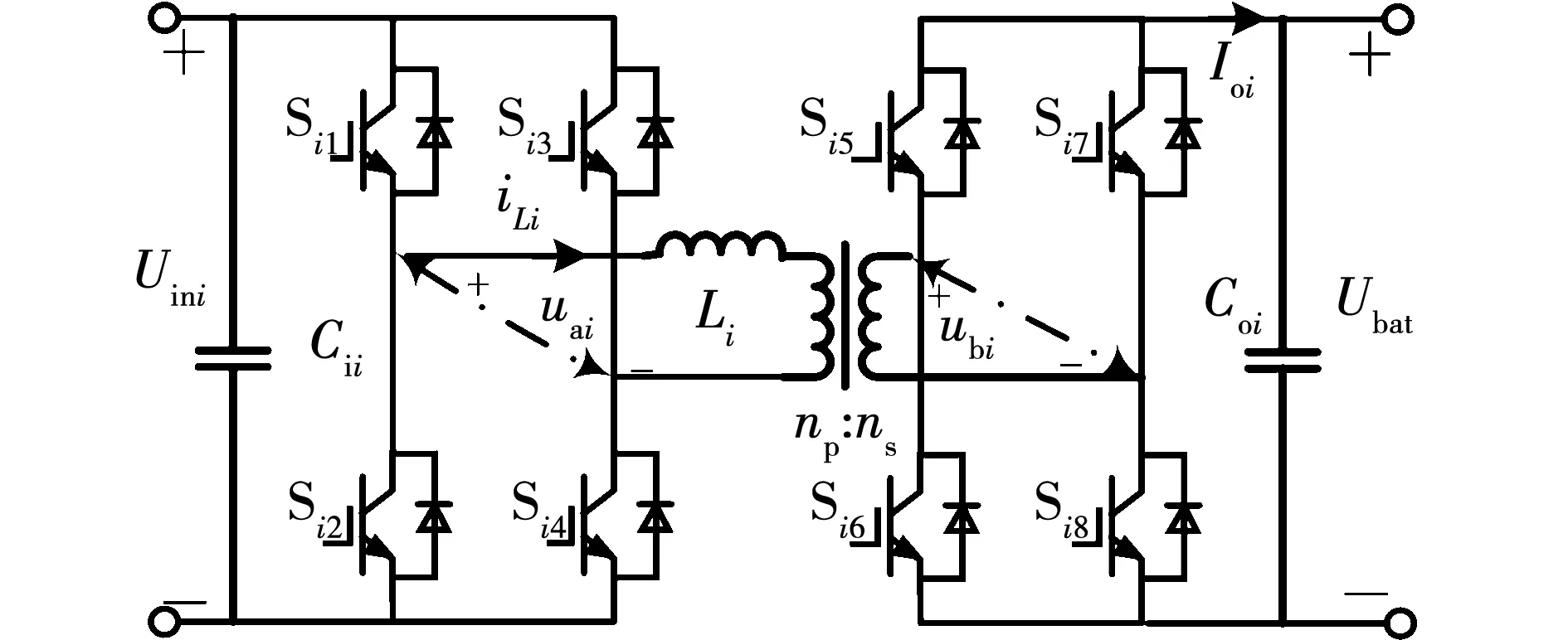
图2 DAB#i变换器拓扑Fig.2 Topology of DAB#i converter

图3中：Ts表示相应开关方波驱动信号的一个开关周期；Ths为半个开关周期；Di为一次侧和二次侧交流方波电压uai和ubi外移相比。由其电感和各自的电桥交流方波电压组成一个闭合内环，由KVL原理，可得表达式为：

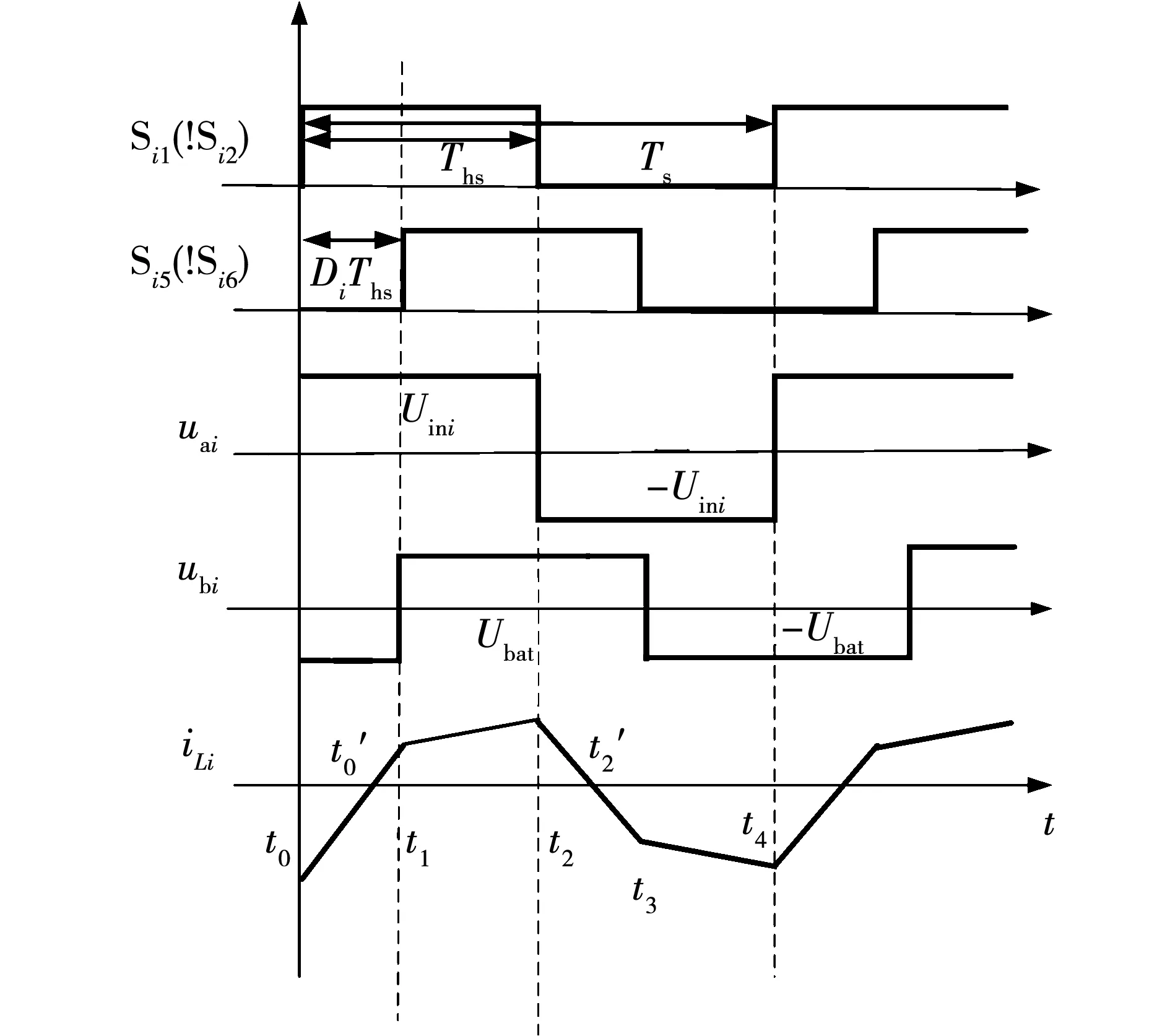
图3 单重移相调制下的理论波形Fig.3 Theoretical waveform under single phaseshift modulation

(1)

式中{Si1,Si2,Si5,Si6}=1或0。

由式(1)可知电感电压在一周期内有4个值，同时，在稳态运行期间，电压uai和ubi以及电感电流iLi每半个周期幅值相同但符号相反。即表示电感电压每半个周期大小一致、符号相反，由电感两端电压和电流相互关系，前半个周期的转移功率与整个周期内转移功率大小相同。在前半个周期内，电感电流的变化过程可分为电感电流快速上升阶段(t0-t1)和电感电流缓慢上升阶段(t1-t2)，各时间段电感电流表达式为：

(2)

式中：iLi(t0)、iLi(t1)分别为t0时刻、t1时刻电感电流；K为变压器变比，K=np/ns。由t1-t0=DiThs,t2-t1=(1-Di)Ths可得t1和t2时刻电感电流为：

(3)

由于ii(t)在正负半个周期上是对称的，有iLi(t0)=-iLi(t2)，代入式(3)中可得

(4)

式中fs为开关频率，fs=1/Ts。结合式(1)～式(4)，在正向工作时，半个周期内感应电流的表达式为：

(5)

根据上式可以计算模块正向功率传输时的平均输出功率表达式为

(6)

通过控制Di和开关周期即可控制电感电流的大小，从而改变传输功率的大小。

2 ISOP-DAB变换器的控制策略

在图4中，Sij表示DAB#i开关Si1～Si8，控制系统通过采样处理得出的蓄电池电压Ubat选择恒流控制或下垂限压控制，然后通过单移相调制的触发控制改变DAB模块各功率开关的通/断。

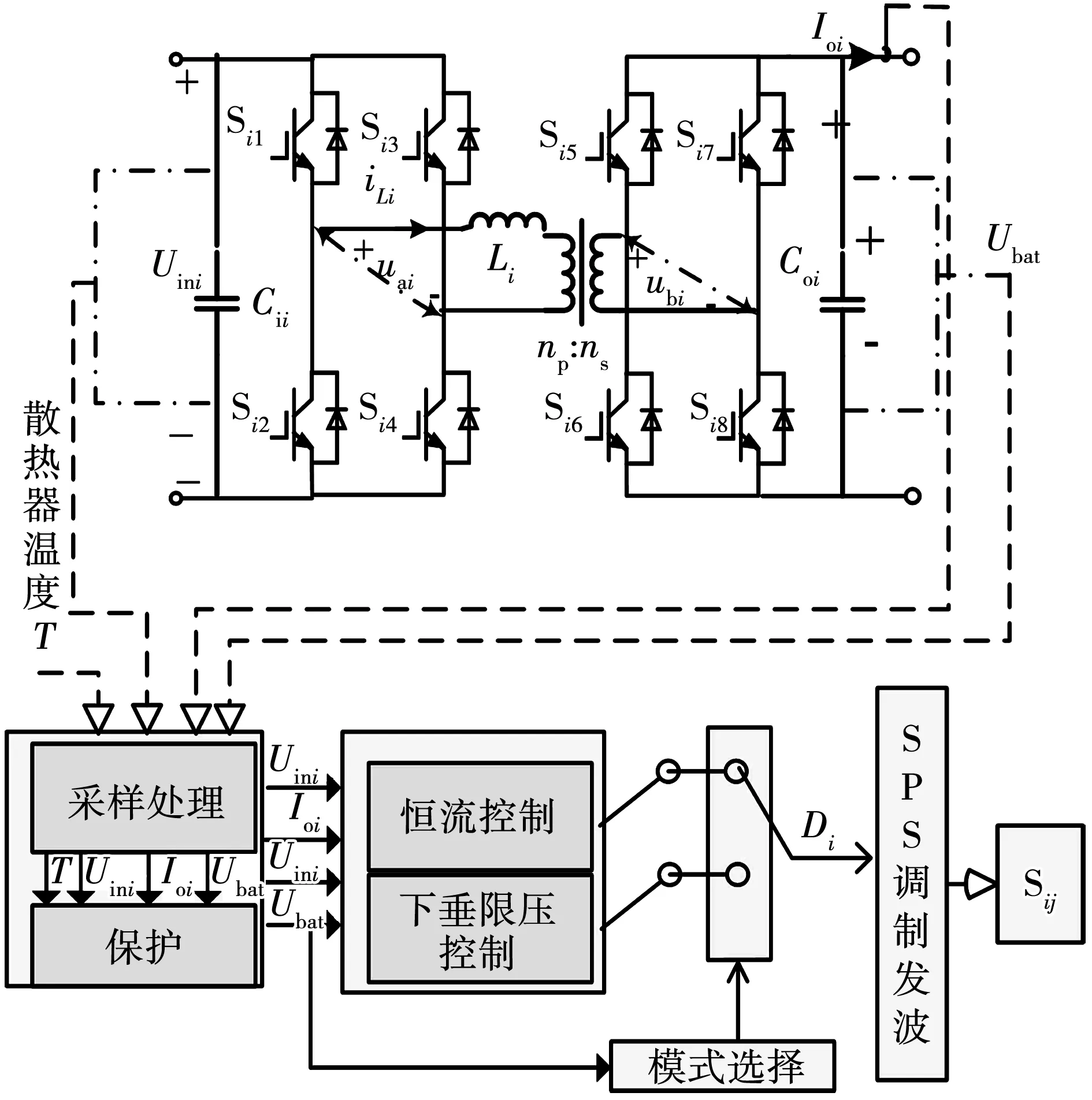
图4 DAB#i的控制系统示意图Fig.4 Control system diagram of DAB#i

2.1 恒流控制

由式(6)可知，DAB的输出功率与输入电压、移相比、变压器匝比等相关，可以通过调节移相比来控制。根据式(6)可以推导出移相比与电流参考值之间的关系式为

(7)

为了实现DAB的输出无静差控制，在移相比计算的基础上，还需要通过PI调节器来补偿功率损耗等因素造成的误差，此外考虑到ISOP-DAB变换器的输入均压[12]，还需要在模块电流控制的基础上添加输入均压控制。根据上述要求，本文所提的ISOP-DAB变换器中DAB#i模块恒流控制如图5所示。

图5 DAB#i恒流控制框图Fig.5 Constant current control diagram of DAB#i

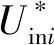
2.2 下垂限压控制

对于单个DAB变换器的恒压控制，一般通过单电压闭环控制即可，而针对ISOP-DAB变换器需对DAB模块的控制环路加入输入均压环。同时，由于蓄电池恒压充电时，电压是在不断升高的，电流不断减小，为保证输出参考电压在一定范围浮动追踪蓄电池电压。参考直流微电网下垂控制的控制策略，对ISOP-DAB变换器中DAB#i引入下垂系数。由此得到其下垂限压控制框图如图6所示。

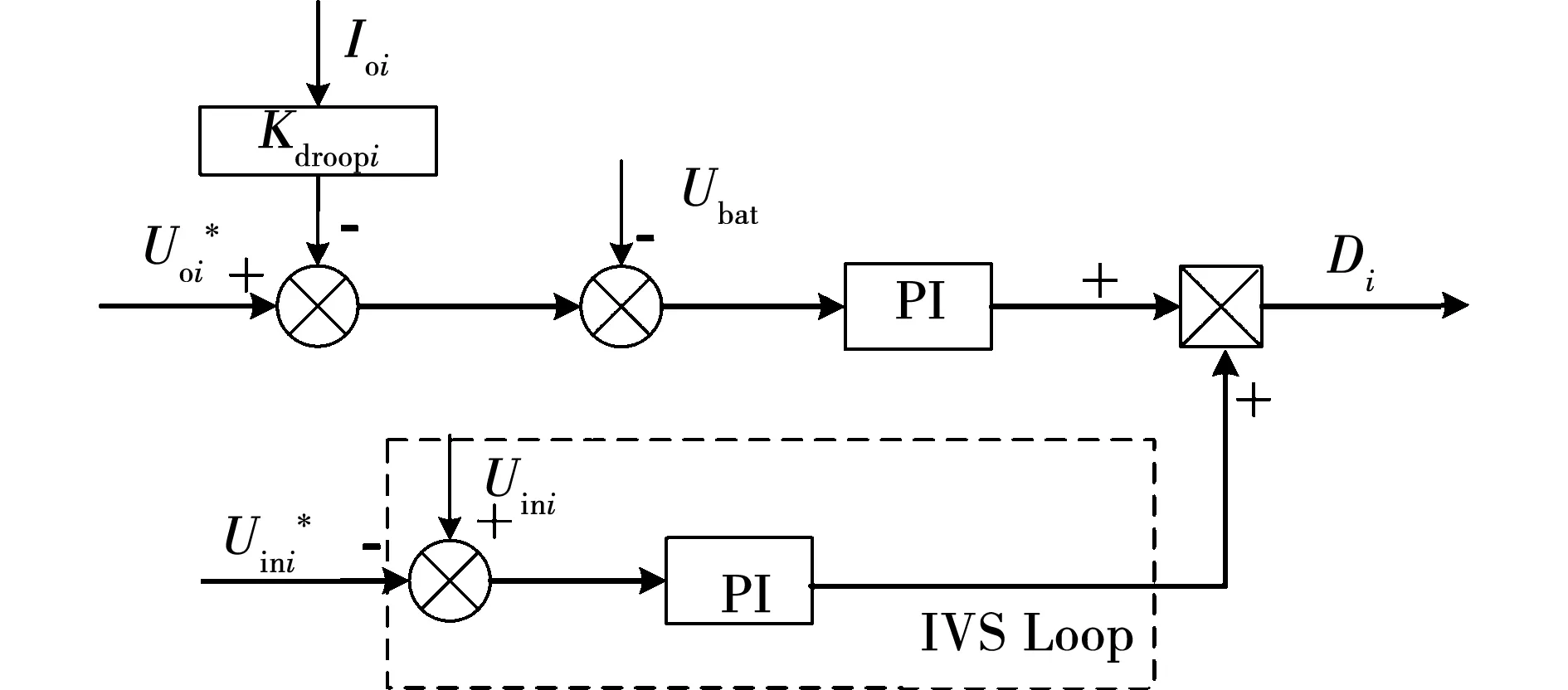
图6 DAB#i下垂限压控制框图Fig.6 Droop voltage limiting control diagram of DAB#i

图6中Kdroopi表示下垂系数，考虑到前期恒流充电的影响和后期蓄电池耐压程度，下垂系数应满足以下关系：

(8)

式中：Ubat1表示恒流充电完成时所设置的参考电压，一般为蓄电池标定充电状态(state of charge，SOC)100%时的最大电压与额定电压之和的一半；Ubat2为恒压充电完成时所设置的参考电压，要在蓄电池极板所能承受的电压范围内。

3 控制回路分析

测试电源采用的ISOP-DAB变换器，实现各模块输入均压(input voltage sharing, IVS)或输出均流(output current sharing ,OCS) 即可实现系统功率平衡[11-12]。上述的恒流控制和下垂限压控制策略是两种不同的控制回路，可以根据小信号电路推导其控制回路传递函数。忽略电路损耗，在ISOP-DAB变换器正常运行时，单个模块的输入功率等于输出功率，因此，模块的输入输出平均电流可表示为：

(9)

在静态工作点附近施加扰动，这样可以得到输入、输出电流为：

(10)

同理对Uini、Ubat、Di施加扰动，同时将其代入式(9)，并进行简化计算可得：

(11)

式中m1～m4分别为：

(12)

假定ISOP-DAB变换器模块参数一致，可得其建立相应小信号模型如图7所示。图中rin=RoK2,m1～m4为该模块相应系数。通过小信号电路可推导各控制回路的传递函数。

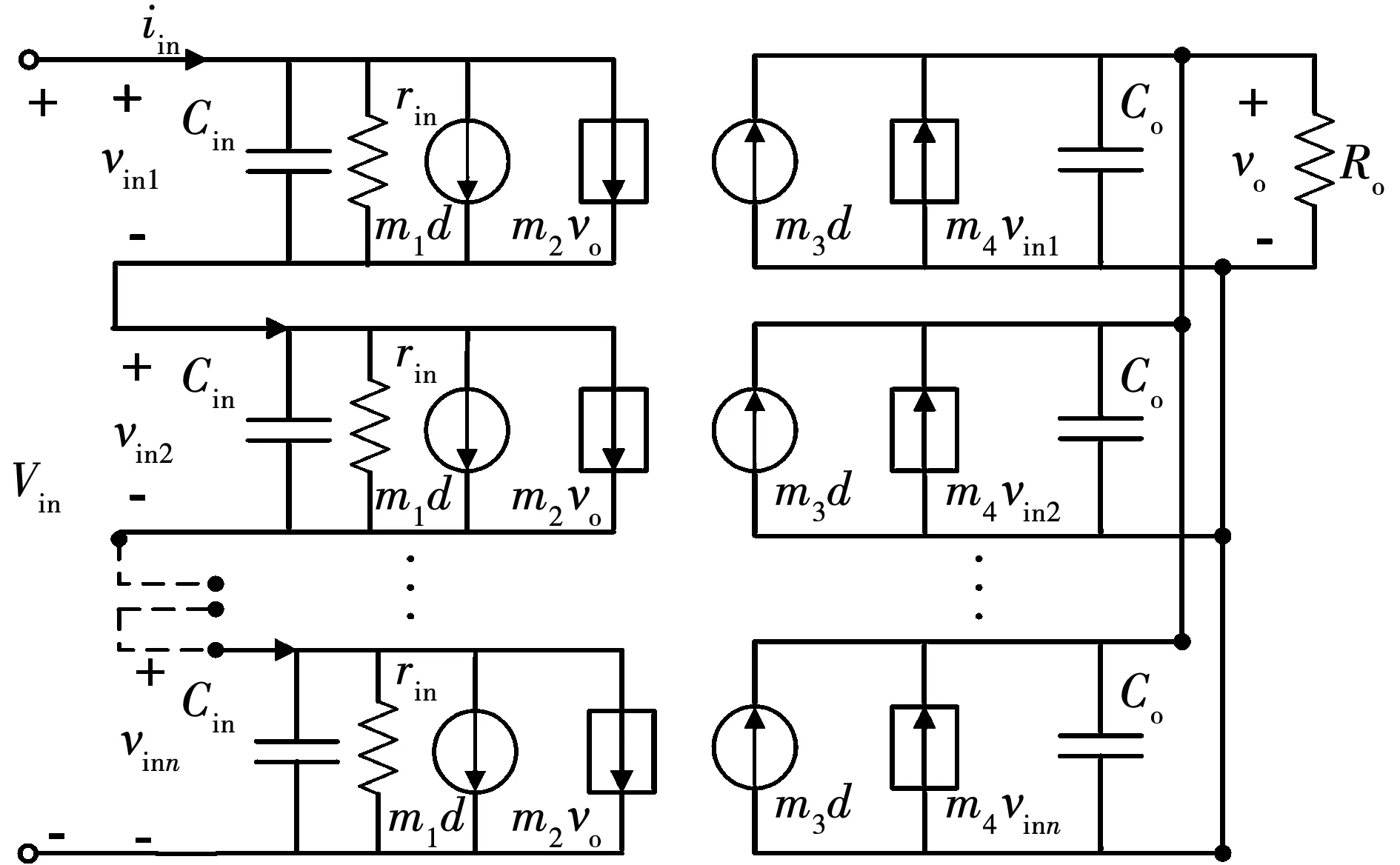
图7 ISOP-DAB变换器小信号电路图Fig.7 Small signal circuit diagram of ISOP-DAB converter

3.1 恒流控制回路分析

为了简化分析图5所示的恒流电流控制策略，忽略移相比计算单元的影响，输入电压闭环控制作为控制外环，此时，输出电流闭环控制器Gm(s)与输入电压均压闭环控制器Gn(s)作相应转换，获得恒流控制等效双闭环图，如图8所示。

图8 恒流控制等效双闭环图Fig.8 Equivalent double closed loop diagram of constant-current control

在图8中，Gio(s)为输出电流对移相比控制信号的小信号传递函数，而Ggi(s)为输出电流对输入电压的传递函数。由图7可知：

(13)

(14)

如图8所示，输入电压闭环是外环，内环是输出电流闭环。内环输出电流开环转换函数Giop(s)、内环闭环传输函数Gioc(s)和外环开环传输函数Gvinco(s)分别表示为：

Giop(s)=Gm(s)Gio(s)；

(15)

(16)

(17)

3.2 下垂限压控制回路分析

同理可简化分析图6所示下垂限压控制策略，通过相应转换输出电压控制器Gk(s)和输入电压均压控制器Gp(s)，可以获得下垂限压控制等效双闭环图，如图9所示。

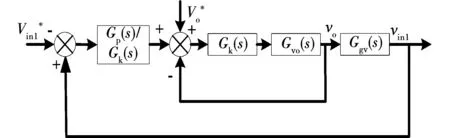
图9 下垂限压控制等效双闭环图Fig.9 Equivalent double closed loop diagram of droop voltage-limiting control

在图9中，Gvo(s)为输出电流对移相比控制信号的小信号传递函数，Ggv(s)为输出电压对输入电压的小信号传递函数。由图7可知：

(18)

(19)

如图9所示，外环为输入电压闭环，内环为输出电压闭环。内环输出电流的开环传递函数Gvop(s)、闭环的内环Gvoc(s)和外环的开环传输函数Gvinvo(s)分别表示为：

Gvop(s)=Gk(s)Gvo(s)；

(20)

(21)

(22)

由上分析已知控制回路的开环和闭环传递函数，通过与传递函数bode图形相结合的方法，可以对控制器进行参数的设计。内环控制器补偿后的开环传递函数幅频特性曲线的截止频率应达到开关频率的1/20～1/10。控制环路中，输入电压环作为辅助调节控制，以确保各个单元之间的功率均衡。因此，输入电压开环传递函数截止频率应小于其内环传递函数截止频率。同时，控制器补偿后内外开环传递函数Bode图在0频率点的增益应足够大，以确保系统的稳态误差逼近0，其相位裕度应小于180°，保证控制系统的稳定性[13]。

4 系统控制器设计及仿真实验

根据文献[14]针对单节12 V/12 Ah胶体铅酸蓄电池的相关等效二阶模型，电池可看作71.03 mΩ大小的等效电阻Ro。本文设计的ISOP-DAB变换器由两模块组成，每个模块最大传输功率为700 W。电路主要参数如表1所示。

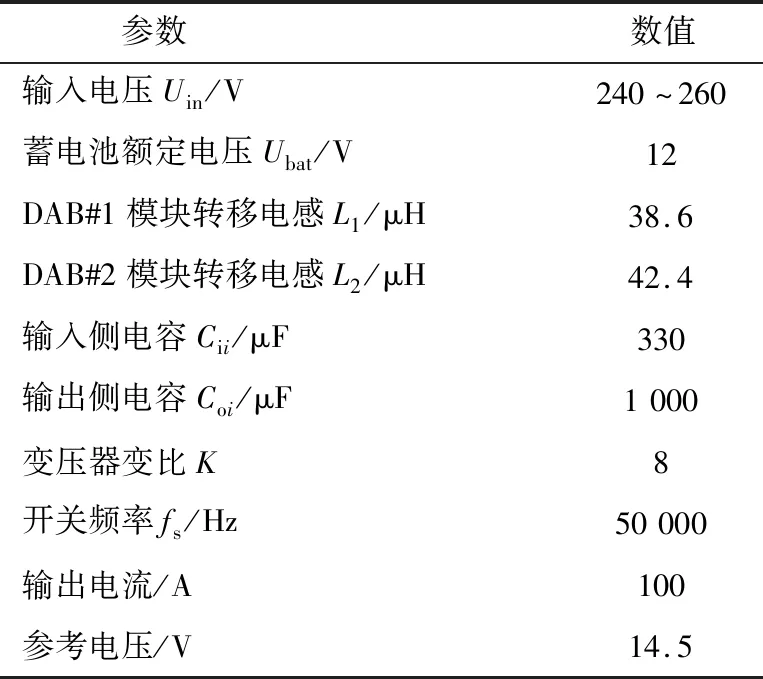
表1 仿真模型的参数Table 1 Parameters of simulation model

4.1 系统控制器设计

结合上述环路分析，以DAB#1为例，将表1中的相应参数代入式 (15)～式(16)和式(18)～式(19)，分别得到传递函数Gio(s)、Ggi(s)和Gvo(s)、Ggv(s)。以传递函数伯德图作辅助，设计恒流控制和下垂限压内外环控制器Gm(s)、Gn(s)和Gk(s)、Gp(s)。相应的控制内外环补偿前后开环伯德图如图10～图13所示。

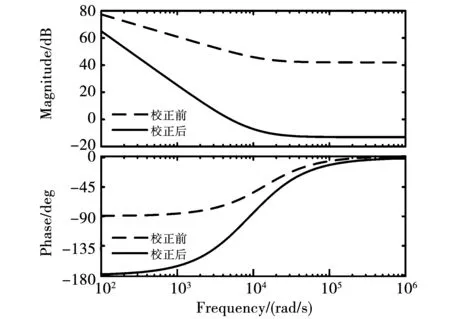
图10 电流控制内环开环伯德图Fig.10 Open-loop bode diagrams of current control inner loop

测试电源的ISOP-DAB变换器接受单相 PWM整流器所提供的输出电压，主要含有二倍工频脉动。因此，外环控制器被设计成使外环开环传输函数的截止频率低于100 Hz进行抑制。由图10、图11可知，校正后其伯德图显示低频处有高增益，高频处有衰减，小于开关频率，证明了PI控制的有效性[15]。内环截止频率远高于外环，相位裕度也大于180°。同样地，由图12、图13所示下垂限压控制下的内外环伯德图可知，控制器的设计满足稳定控制系统相关要求。在此控制方法下，输入即使经过一定时间的调节，两个模块的输入电压也会相等，系统重新进入稳态[16]。

图11 电流控制外环开环伯德图Fig.11 Open-loop bode diagrams of current-controlouter loop

图12 下垂限压控制内环开环伯德图Fig.12 Open-loop bode diagrams of droop limiting voltage-control inner loop

图13 下垂限压控制外环开环伯德图Fig.13 Open-loop bode diagrams of droop-limiting-voltage-control outer loop

4.2 仿真实验结果

在MATLAB/Simulink仿真平台上建立了本文描述的ISOP-DAB转换器，在两种控制策略下对12 V/12 Ah铅酸蓄电池进行充电。对控制系统进行验证，暂不考虑其两种控制的实际切换，因此在恒流控制策略下，设定蓄电池初始SOC为30%，在下垂限压控制策略下，设定蓄电池初始SOC为80%。初始输入电压设置为240 V，在0.065 s时刻，输入电压调整为260 V，再经过0.065 s输入电压重新回到240 V。仿真实验波形图如图14～图17所示。

图14 恒流控制下模块1，2输入电压波形Fig.14 Input voltage waveforms of module 1 and 2 under constant-current control

图14、图15表明在输入均压环的作用下，当输入电压为240 V时，DAB#1和DAB#2的输入电压均为120 V。当输入电压变为260 V时，各模块输入电压均为130 V，同时输出电流达到目标值100 A。

图15 恒流控制下输出电流与蓄电池电压波形Fig.15 Output current and battery voltage waveforms under constant-current control

由图16、图17可知ISOP-DAB变换器在下垂限压控制下的输出特性和功率平衡特性都得到了保证。同时图17表明蓄电池下垂在恒压控制下，充电电流会渐渐递减，满足在充电后期逐渐限流的工作要求。

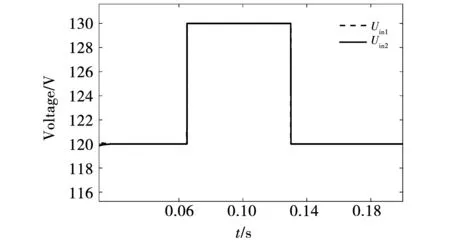
图16 下垂限压控制下模块1，2输入电压波形Fig.16 Input voltage waveforms of module 1 and 2 under droop-limiting-voltage control

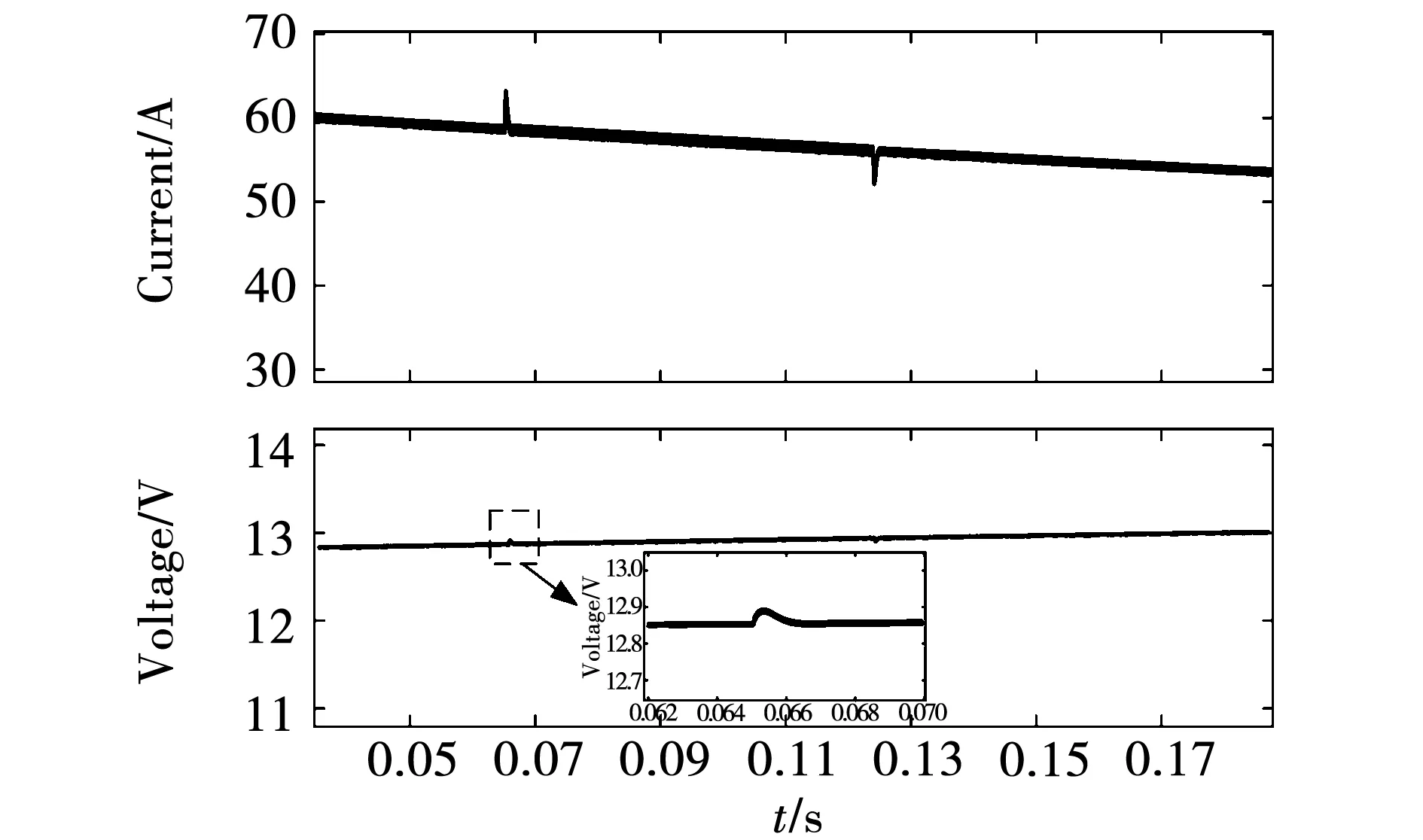
图17 下垂限压控制下变换器输出电流与蓄电池电压波形Fig.17 Output current and battery voltage waveforms of converter under droop-limiting-voltage control

分别以自校正特性、解耦和离散化方法控制ISOP-DAB变换器输入电压均分，模块DAB#1的输入电压变化如图18所示。

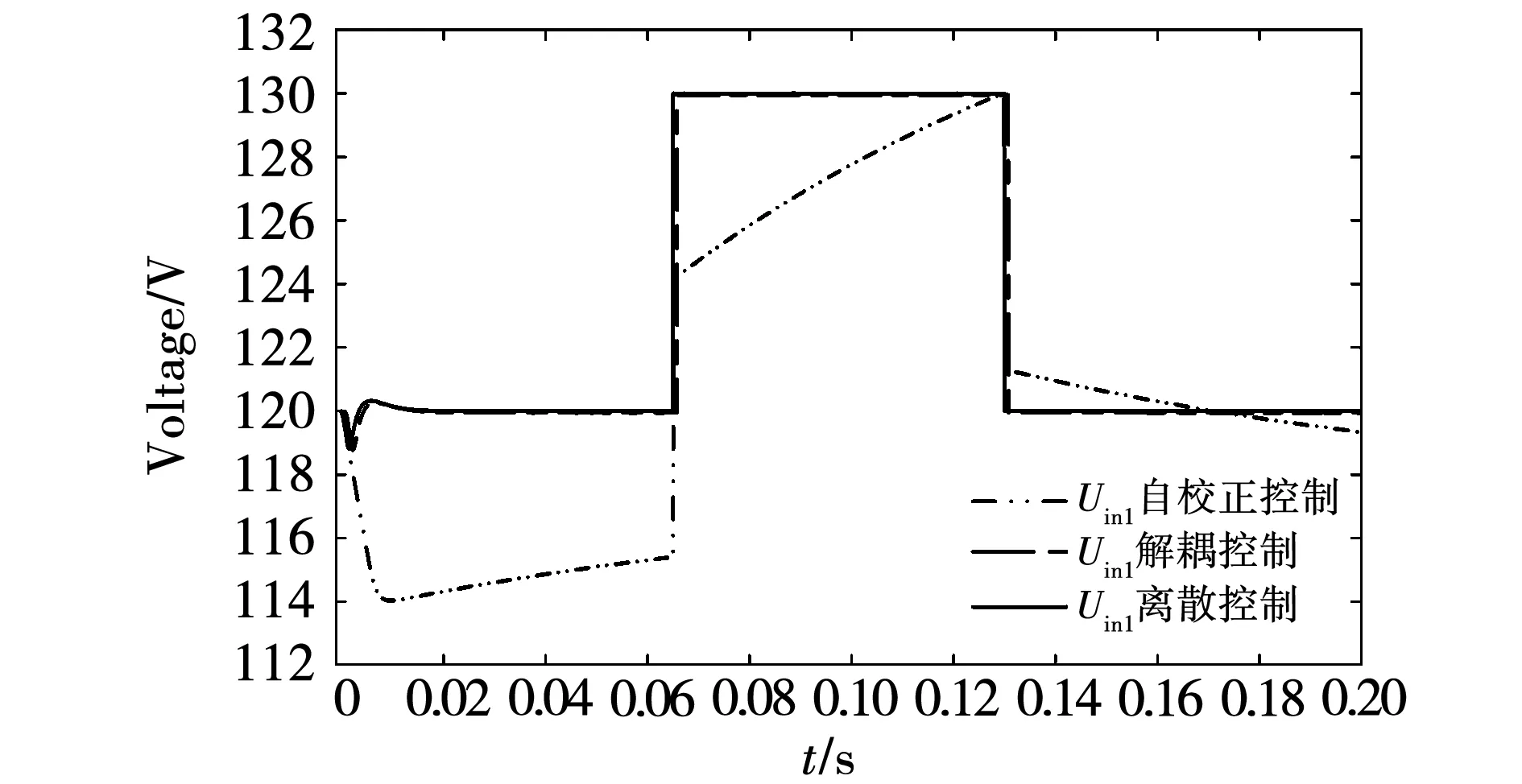
图18 不同控制方法下DAB#1的输入电压Fig.18 Input voltage of DAB#1 under different control methods

若以自校正特性均分输入电压，模块有校正的趋势，但得不到理想结果。解耦和离散化方法控制性能一致，但解耦方法下各模块控制集中，模块化程度低。

5 结 论

本文针对传统测试电源多采用单向能耗式结构，存在充放电测试速度慢、能耗高的问题，提出基于ISOP-DAB变换器的测试电源方案，结合蓄电池充电要求，在不同的充电阶段实现恒流输出和限压输出控制。并考虑到输入电压和输出之间的耦合关系，以“从内到外”的设计原则设计控制器，做伯德图简化设计过程。通过ISOP-DAB 变换器的仿真实例，验证了所提ISOP-DAB模块化控制方法的有效性。