基于ANSYS的内涵道测量耙模态计算模型简化研究*

于 浩

(中国飞行试验研究院,陕西 西安 710089)

0 引 言

航空发动机测量耙可以用来测量发动机试飞过程中发动机流道内的压力和温度参数，如果测量耙的固有频率与发动机的振动频率或气流激振频率相同，就会产生谐振[1-3]。当谐振发生时，测量耙的使用寿命将会极大缩短，轻则导致设备出现裂纹或损伤，无法获取准确数据，重则发生断裂，导致发动机失效停车，危及飞行安全[4]。测量耙在飞行中主要受气动载荷和振动载荷作用，气动载荷相对较小，静强度满足要求，振动载荷主要来自发动机转子部件，因此在测量耙设计制造过程中要分析其模态，使固有频率避开发动机工作的主要激振频率[5]。

早期的测量耙模态设计主要通过试验迭代的方式进行，即根据工程经验预先设计测量耙，通过试制后进行模态试验获得模态信息，如果试验结果发现该测量耙的固有频率与发动机某转子部件的激振频率接近，那么就需要修改该测量耙的整体设计，再进行试制，直到试验设计符合要求。试验迭代的方式在设计过程中没有理论依据，主要依靠工程经验，对工程技术人员的经验要求较高，且当测量耙的结构发生比较大的改变时，效果较差，设计周期长，研制成本高。

随着有限元分析技术的不断发展，现在测量耙设计过程中也采用有限元方法分析模态，根据设计尺寸和材料参数等建立有限元分析模型，通过模态分析计算得出测量耙的固有频率，将计算结果与发动机工作的主要激振频率对比，如果结果相近则修改设计，重新计算直到计算结果符合设计要求[6]，再进行样品试制，通过试验进一步验证有限元分析法的可用性。这种方法相比于传统试验方法极大地降低了测量耙设计难度，缩短了研究周期也节省了经费。

但是由于有限元仿真模型与实际制造的真实部件存在一定差异，同时建模过程通常需要对一些模型细节做出一定的简化，这种简化一般参考以往的工程经验，这种方式对于结构简单、根部固定安装的测量耙影响较小，但是对于结构复杂、穿越内外涵道安装的测量耙来说，计算结果与试验结果往往相差较大，甚至某型测量耙在试验后发现其一阶固有频率与发动机的激振频率相重合，这对任务的完成周期造成了极大影响。为探究此类内涵道测量耙的有限元建模方法，提高计算结果准确性，笔者基于ANSYS平台，考虑内部管路及填充结构、根部连接、限位孔约束对测量耙固有频率影响，对比分析了9种不同的有限元模态计算模型，获得了内涵道测量耙模态分析相对最优化的建模方法。

1 测量耙的模态计算建模方法

发动机测量耙的主要结构有：耙体、底座、测头、引气管路、线缆、内部填充物等。如图1所示。由于其结构复杂，在对测量耙进行模态计算时，有必要对一些结构进行适当的简化，以降低模型的复杂程度，节约计算资源，降低计算时间。

图1 某型测量耙

一般情况下，对测量耙模型进行简化时通常以工程经验为主，例如不考虑内部引气管路结构、内部填充物等，对这些简化方式所带来的计算误差并没有进行过比较详细的分析。因此计算结果可能会与实验结果有较大偏差。

在对测量耙进行模态分析过程中常用的模型简化方法主要有以下三类。

(1) 简化测量耙内部结构：忽略测量耙内部的复杂引气管路、填充物。

(2) 简化连接方式：在实际加工过程中测量耙的底座与耙体采用边缘焊接的方式连接，在计算中一般将底座与耙体建立为一个整体模型。

(3) 简化约束方式：对于单支撑的悬臂测量耙，通常采用的约束方式为测量耙的安装座底面固支，而对于前端通过限位孔约束的内涵道测量耙来说，前端也采用限位孔固支的方式进行固定。

针对以上三类常见的测量耙建模简化方法，文中以某型内涵道测量耙为研究对象，通过建立多组不同的有限元模型进行计算，对比分析了不同的建模简化方式对计算结果的影响。

2 算例分析

仿真选用的模型为一种比较有代表性的内涵道测量耙模型—某发动机压气机出口总温总压测量耙，该测量耙耙体为不锈钢材料，内部引气管路为不锈钢材料并以胶体填充，底座与耙体之间以焊接的方式连接在一起，测量耙底座安装在外涵机匣上，前端通过限位孔穿过内涵机匣将受感部置于内涵道中，限位孔也对测量耙的前端起到支撑固定作用。其结构如图2所示。

图2 某型测量耙三维结构模型图

该型测量耙在设计完成后进行了振动试验件试制，并通过试验件的振动试验测量了耙在5～2000 Hz下的主要共振频率，在气流方向的扫频结果显示，在5～2000 Hz范围内测量耙的共振频率点为1阶458.61 Hz，二阶1 403.02 Hz。

2.1 耙体内部简化的影响

测量耙内部结构处理方式主要有以下三种：①全简化：忽略内部引气管路以及填充的胶体材料；②部分简化：忽略内部引气管路，用填充的胶体材料替代；③等效质量简化：忽略内部引气管路，用胶体材料替代的同时保证替代部分的等效质量相同。

为了对比分析以上三种简化方法对计算结果的影响，建立了带有内部引气管路的有限元模型，三种模型如图3所示。

图3 不同测量耙内部结构模型

根据实验室测量耙的安装方式对测量耙进行约束，由于不同的约束条件对计算结果有较大影响，因此在以上模型的计算中统一采用底座螺栓孔固定约束，前端限位孔固定约束的方式。如表1所列为4种不同的有限元模型对X轴方向前2阶固有频率的计算结果。

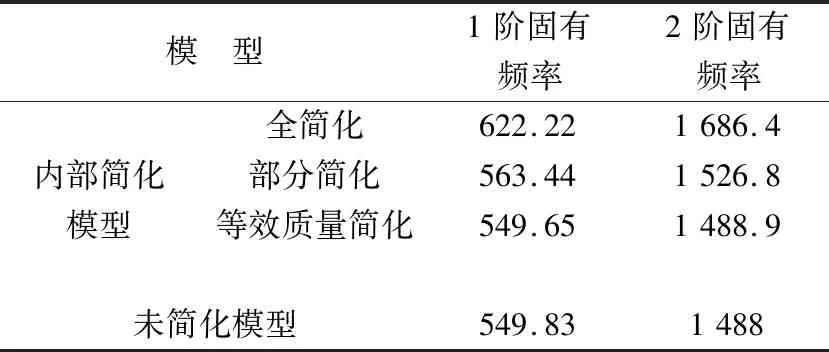
表1 不同简化模型气流方向前2阶固有频率对比

不同模型气流方向前2阶固有频率的振型相同，如图4所示。

图4 测量耙气流方向前2阶模态振型图

对比发现，当内部结构全简化时，由于整体质量偏低，造成计算结果比实际结果偏高，在相同的约束条件下，全简化模型比未简化的模型一阶固有频率高13.17%，使得全简化模型的计算结果不能作为结构设计过程中固有频率确定的依据；部分未简化模型计算结果比完整内部结构模型偏高2.5%，说明计算时将内部引气管路与填充物部分简化不会显著影响模态分析结果。为了减小因引气管路和内部填充胶体的质量不同引起的计算误差，采用内部填充物等效质量的方法使等效后的内部附加质量与完整内部结构保持一致，计算结果表明，等效质量的方法与内部完整结构模型在前2阶固有频率基本一致，因此等效内部填充物质量的方法是一种能够减少建模工作量且计算结果偏差较小的测量耙内部结构处理方式。

2.2 耙体与底座连接形式简化的影响

在测量耙的实际加工过程中，测量耙的耙体和底座之间的连接方式为根部焊接方式，耙体穿过底座的中孔，根部与底座焊接。耙体与中孔有一定的间隙，但是在进行有限元分析时，二者往往被视作一个整体。为研究这种建模方式对仿真计算结果的影响，建立了如图5所示的带有焊接结构的测量耙有限元模型，在底座和耙体之间设置1 mm的间隙，并用建立焊接体的方法来模拟真实的耙体和底座的装配情况。模型示意图如图5所示，模型内部为等效质量胶体，前端约束方式为限位孔固定约束。

图5 有焊接结构的有限元模型

采用根部焊接结构和整体结构的模型计算结果如表2所列，仿真分析表明，根部焊接结构对测量耙固有频率存在影响，其固有频率低于不考虑焊接间隙的整体结构模型。整体结构模型比根部焊接结构模型的1阶固有频率高3.5%，表明采用根部焊接结构模型能够更加准确地计算测量耙1阶固有频率。

表2 不同底座连接形式模型前2阶固有频率

2.3 耙体前端支撑约束方式的影响

对于具有前端支撑结构的耙体来说，前端支撑结构的约束方式对模态分析的结果影响较大，以文中测量耙为例，其前端的支撑方式为限位孔约束。限位孔和测量耙之间可以沿着孔的轴向滑动，且限位孔与测量耙之间存在配合间隙，在试验振动过程中，测量耙与限位孔之间处于一种非线性变刚度的状态，因此很难使仿真计算的约束条件与实验保持一致。

为研究前端约束方式对计算结果的影响，分别采用限位孔处刚性约束、限位孔处位移约束以及前端弹性支撑的方式计算了测量耙气流方向前2阶固有频率。模型内部为等效质量胶体，耙体与底座的连接为焊接结构。计算结果如表3所列。

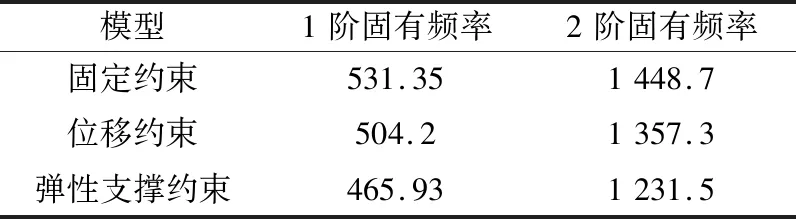
表3 前端不同支撑方式模型前2阶固有频率

从表中可以看出，前端的支撑方式能够极大地影响该型测量耙的固有频率，采用限位孔弹性支撑约束模型的1阶固有频率为465.93 Hz，相比于采用限位孔处弹性约束模型，位移约束和固定约束的计算结果分别偏高9.2%和15%。与实验结果对比可知，采用限位孔弹性支撑约束模型的一阶固有频率与实验结果最为接近，仅偏高1.7%，但是2阶固有频率相比于实验结果偏低12%，而采用限位孔位移约束的模型的2阶固有频率与实验结果最为接近，偏差3.25%，考虑到在实际使用过程中更加关注测量耙的1阶固有频率，因此采用限位孔弹性支撑的方式来计算该类型测量耙为最优选择。

3 结 论

为研究测量耙仿真建模方法对固有频率计算结果的影响，文中以某发动机内涵道总温总压测量耙为研究对象，分别考虑内部管路及填充结构、根部焊接、限位孔约束对测量耙固有频率的影响，共建立了9种不同的有限元模型，并进行模态分析，得出以下结论。

(1) 忽略测量耙内部结构会导致频率计算结果偏高，利用等效质量方法将内部管路与填充物简化为整体模型，计算结果与采用完整内部模型时基本相同，该方法可以作为内部存在复杂结构的测量耙的模型简化方法使用。

(2) 对于根部与底座焊接的测量耙，在建模时考虑焊接部位的影响可以提高频率分析结果的准确性。

(3) 具有前端限位孔约束结构的测量耙，限位孔处的约束方式对计算结果影响较大，采用限位孔弹性支撑约束时，测量耙1阶固有频率与试验结果最为接近。

(4) 对于带有前端支撑、根部焊接结构的测量耙，采用内部结构等质量简化、根部焊接、限位孔弹性支撑建模的方式进行频率分析是最优化的建模方法。