某作动器的正弦振动分析与试验验证*
2022-09-14段智朝
喻 琴,杨 凯,段智朝,张 闯
(庆安集团有限公司航空设备研究所,陕西 西安 710077)
0 引 言
正弦振动试验分为两类:定频和扫频[1-2]。其中扫频正弦振动试验,分为线性扫描和对数扫描。线性扫描频率变化是线性的,这种扫描用于细找共振频率的试验。对数扫描频率变化按对数变化,低频扫得慢而高频扫得快。
某作动器在进行正弦振动试验时,先进行了Z方向(如图1所示,垂直于试验台台面的方向为Z方向)线性扫描,得到其固有频率。后进行了对数扫描,在进行对数扫描时发生了断裂现象。笔者采用ANSYS Workbench软件,针对某作动器进行了正弦振动分析,并基于Miner线性累计损伤理论,开展正弦振动环境下的疲劳寿命计算,认为该产品的强度较弱,提出了改进方案,后又对改进方案进行计算与试验。
1 某作动器结构与振动条件
某作动器主要由电机、减速箱、滚珠丝杠传动副等部分组成。固定接头和活动接头分别固定在试验台夹具上,如图1所示。

图1 某作动器振动安装示意图
在Z方向进行线性扫描试验:频率10~2 000 Hz、加速度2.0 g、0.5 mm幅值(峰-峰值)。得到作动器Z方向的前三阶固有频率:138、415、1 263 Hz。
接着进行对数扫描试验:如图2中曲线规定的振动量值。在进行了Z方向30 min振动功能后,产品左壳体零件的固定接头耳片发生断裂,如图3所示。
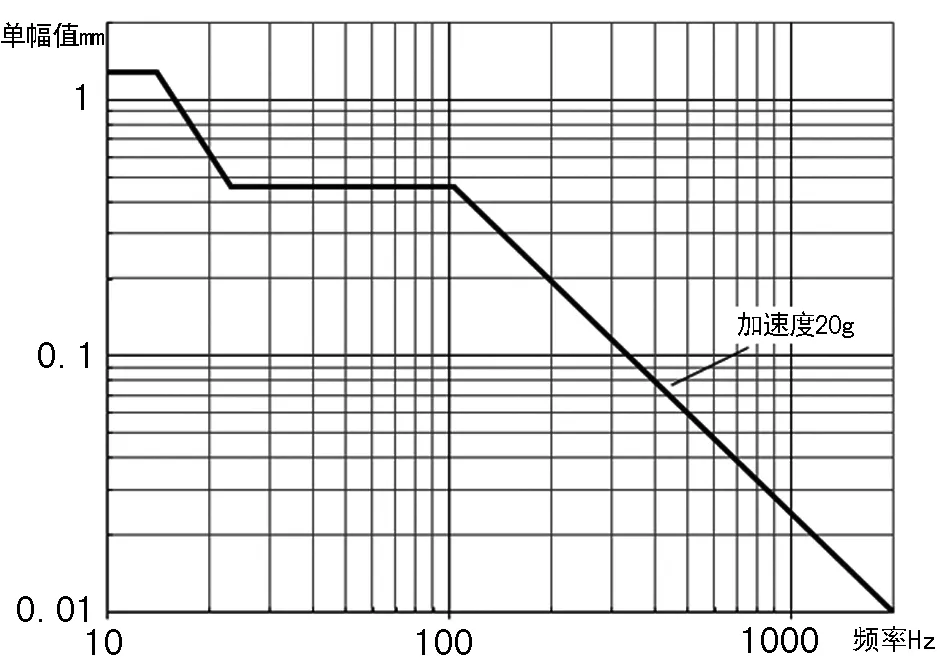
图2 对数扫描试验曲线

图3 左壳体振动试验断裂情况
2 模型验证
模型验证[3]的一般流程如图4所示。

图4 模型验证流程图
模型验证中包括质量点、刚度以及约束的验证。经过图4多次验证,得到最终的简化模型,如图5所示。

图5 有限元模型
质量为5.958 kg(简化前质量为5.95 kg),分别在固定接头和活动接头圆孔处施加固定约束,其中活动接头与关节轴承设置转动运动副,固定接头与关节轴承设置球运动副,如图6(a)、(b)所示。

图6 计算模型
对其进行模态分析,得到前8阶固有频率,见表1所列。

表1 仿真固有频率计算结果
通过质量参与率的比较,得到Z方向前三阶固有频率为:137.08 Hz、436.21 Hz、1 258.9 Hz。由第1节知:通过正弦扫频试验得到作动器Z方向的前三阶固有频率:138 Hz、415 Hz、1263 Hz。Z方向的前三阶仿真固有频率与试验固有频率的比较见表2。
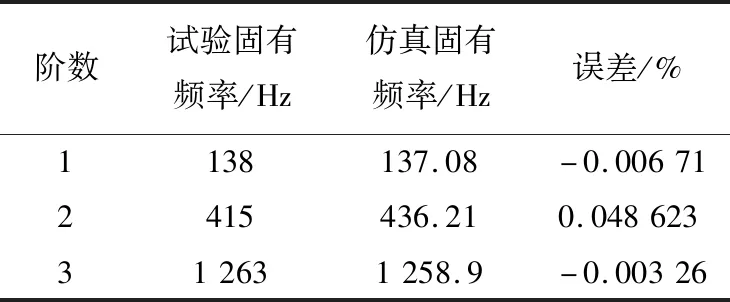
表2 仿真固有频率与试验固有频率的比较
仿真固有频率与试验固有频率的相关性分析时,两者误差在8%左右即可认为两者相关。由表2可知,仿真固有频率与试验固有频率最大误差为0.048%,因此仿真固有频率与试验固有频率吻合度很高,证明了所建有限元模型是正确的,通过模型验证。同时给出了Z方向前三阶仿真固有频率对应的振型,如图7所示。

图7 Z方向前三阶振型
3 正弦振动分析
对作动器展开Z方向正弦振动扫频仿真分析[4],并针对左壳体固定接头耳片计算等效Mises应力,提取应力最大点的应力响应谱,如图8所示。
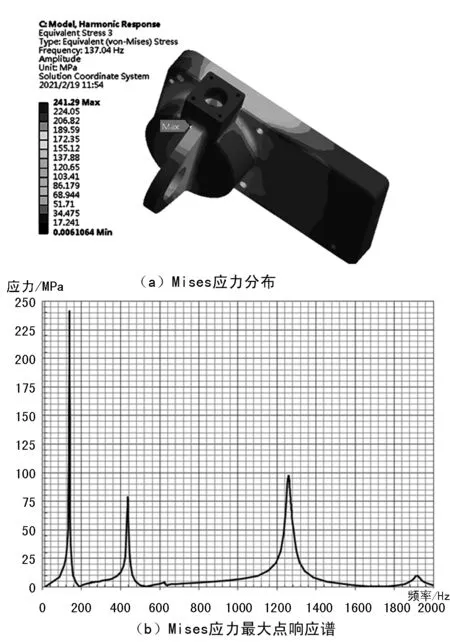
图8 左壳体Mises应力分布及其应力最大点响应谱
经对比,左壳体应力最大点即为产品发生裂纹的位置,如图3所示。
4 基于Miner线性累计损伤的正弦振动疲劳寿命分析
图8所示的危险点的应力-频率曲线,是结构在正弦振动条件下的应力随时间变化的频域描述,因此基于该曲线,结合Miner线性累计损伤理论,可以计算其疲劳寿命。
正弦振动过程中,振动时间、频率和扫描率的关系为:
(1)
上式中R为正弦振动扫描率。
上式等号两侧对f求导数,则有:
(2)
写成离散形式,可得:
(3)
(4)
进一步,可计算Ni如下:
(5)
在多级不同应力幅值σi作用下,各级应力对应的Ni描述如下:
(6)
根据式(2)可得:
(7)
将上式写成离散形式:

(8)
上式中T为正弦振动持续时间,t为单次扫频所需时间。
寿命计算公式为:
(9)
根据Miner线性损伤累计理论,当D<1时,可以认为构件不会发生疲劳破坏,在工程中通常取安全系数为10,即D<0.1,L≥10时,认为构件不会发生疲劳破坏[5]。
基于上一节获得的左壳体固定接头耳片Mises应力最大值点的频率-应力曲线(图8),结合上述理论公式,可以计算左壳体Z方向30 min振动功能正弦振动疲劳寿命,见表3。结果表明左壳体不满足正弦振动疲劳寿命要求,与正弦振动试验结果相符,左壳体耳片发生了断裂,如图3所示。

表3 正弦振动疲劳寿命校核
5 改进方案
将左壳体材料由铝合金2618A-F更改为沉淀硬化不锈钢15-5PH,左壳体固定接头耳片的厚度由7.4 mm增加至13 mm,提高左壳体固定接头耳片的强度。壳体耳片改进后振动仿真情况如图9所示。左壳体Z方向振动疲劳寿命分散系数为9.16E+02>10,壳体振动寿命满足要求。

图9 改进后左壳体Mises应力分布及其应力最大点响应谱
在改进左壳体的同时把振动试验工装也进行了改进,如图10所示。重新进行试验,正弦振动试验合格,说明采取的改进措施切实有效。
6 结 论
针对某作动器的固定接头耳片在正弦振动试验中发生断裂,文中开展了正弦振动疲劳分析,主要结论如下。
(1) 建立了作动器结构的有限元分析模型,基于正弦扫频试验获得Z方向前3阶的固有频率,对模型进行了修正,修正后的分析结果与试验数据的一致性较好。
(2) 根据正弦疲劳寿命计算公式,结合正弦分析获得危险点应力—频率曲线,对耳片进行了疲劳寿命预测,结果表明,左壳体不满足正弦振动疲劳寿命要求,且最危险位置与试验结果相符。
(3) 根据仿真计算结果,对材料和尺寸进行了改进,提高了左壳体固定接头耳片的强度,其Z方向振动疲劳寿命分散系数为9.16E+02>10,重新进行试验后,正弦振动试验合格,说明采取的改进措施切实有效。
