纵向组学数据统计分析方法和研究策略*

吕嘉丽 范冰冰 魏梦珂 张 涛△

近年来，随着高通量检测技术与机器学习方法的发展，以前瞻性队列设计为基础的纵向组学研究已经成为系统生物学研究新趋势[1]。统计学上，纵向数据统计分析方法已经形成了系统的统计分析框架，但这些方法主要集中于变量数目小于观察单位数的低维医学纵向数据[2]。而针对纵向组学数据，目前仍缺乏成熟的统计分析策略。本文拟对近年来国内外研究者提出的纵向组学数据统计分析方法进行介绍，并系统地总结各个方法的核心思想及优缺点，给出纵向组学数据统计分析策略。

纵向组学研究设计与数据特点

在不同的生命及疾病状态下，机体组学标记物浓度处于连续动态变化过程。纵向组学研究设计是指在疾病发生发展过程中或采取干预措施后采集多个时间点的生物标本，进行高通量组学检测。该研究设计可以分析组学标记物的动态变化规律，探讨生物体对危险因素累积的反应过程及疾病发生发展机制。

在数据特点上，纵向组学数据包含个体、时间、组学标记物、相关暴露因素及结局测量信息(如表1所示)。纵向组学数据具有以下特征：(1)非平衡性：不同观察单位随访时间点不一样，同一观察单位间的随访间隔也不一样；(2)自相关性：同一观察单位的不同测量变量之间具有复杂的相关与因果调控关系；(3)测量误差：组学研究常常需要借助高通量检测仪器完成生物样本测量，数据集难免存在由于测量误差引起的变异；(4)时依混杂：在纵向组学研究中，组学测量数据及环境暴露因素均随时间而动态变化，会对因果效应估计产生影响；(5)高维灾难：纵向组学数据除具有一般纵向数据特点外，还存在一般高维小样本组学数据的高维灾难问题。

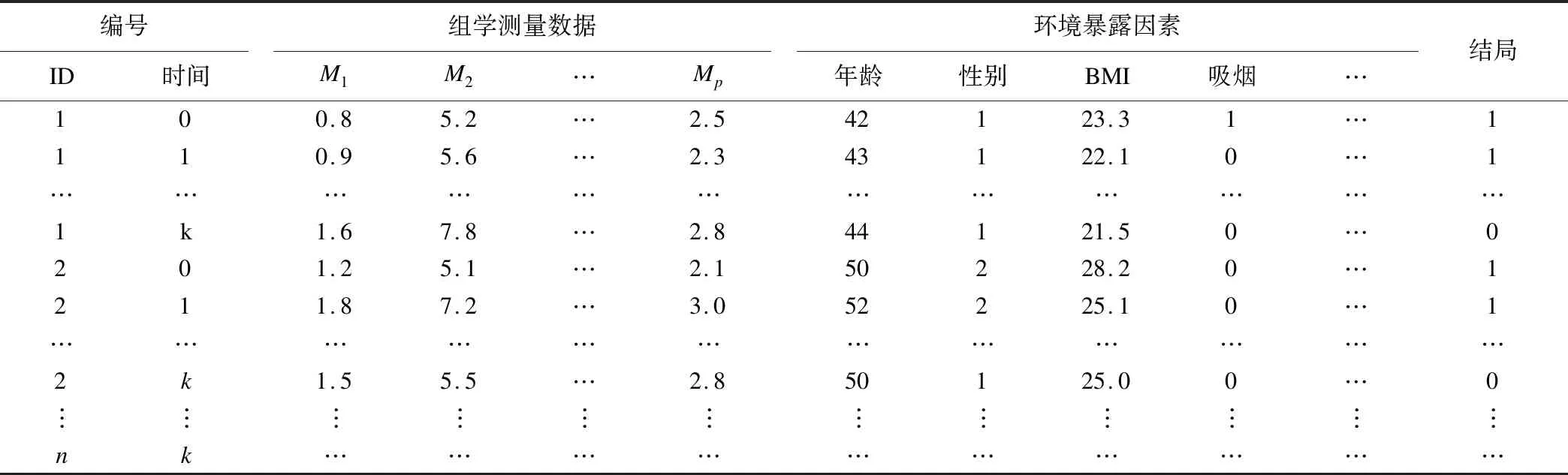
表1 纵向组学数据结构

纵向组学数据常用统计分析方法

纵向组学研究设计的研究目的包括：(1)研究不同组别间组学标记物的动态轮廓差异，发现不同组别间的动态差异组学标记物；(2)研究组学标记物随时间变化的动态趋势；(3)基于动态差异组学标记物，建立预测模型。根据上述研究目标及数据特点，常见纵向组学设计分析方法主要有以下三类[3-5]：(1)单变量统计分析：用于识别随时间变化而改变的差异动态标记物；(2)聚类方法：对标记物的动态变化进行趋势分析，对变化趋势一致的标记物进行聚类；(3)降维方法：考虑到变量间的复杂相关性，利用多变量统计分析方法对高维小样本数据进行降维，发现组学标记物在不同组别间的组学轮廓差异。

1.单变量分析

重复测量方差分析(repeated measures ANOVA) 是早期用于纵向数据分析的方法[6]。目前，混合效应模型(mixed effects models)及广义估计方程(generalized estimating equations)是纵向组学数据分析的常用单变量统计方法[2]。曹红艳等[7]在广义估计方程基础上提出了一种惩罚广义估计方程(penalized generalized estimating equations)，并运用该方法对小鼠进行糖尿病发病关联基因位点筛选。该方法的核心思想是基于LASSO或SCAD等惩罚方法进行广义估计方程建模，不仅保持了广义估计方程的重要特性，同时将该方法推广到高维数据分析，适用于协变量个数p随样本例数n同阶变化的情况。

2.聚类分析

聚类分析(clustering analysis)能同时考察所有变量，识别变化趋势一致、功能相似的组学标记物，对于生物机制的研究具有重要意义[8]。时间序列聚类(time series clustering)根据时间序列相似度对研究对象进行聚类，从而使不同聚类的类间距离最大，类内距离最小。模糊C均值聚类(fuzzy c-means clustering) 是动态组学研究设计中应用最为广泛的一种算法[9-10]。其核心思想是对j个观察单位X={X1，X2…Xj}寻找c个模糊组，并求每组的聚类中心，使得目标函数达到最小。模糊C聚类的优点在于能适应分离性不好的数据集，允许数据性质的模糊性，为数据结构描述提供了详细信息[11]。一项模拟研究表明，相较于K均值聚类算法，模糊聚类算法具有相对较高的聚类效能[12]。但该算法的性能尚依赖于聚类个数和初始隶属度矩阵。

3.降维分析

常用于组学数据的降维方法包括主成分分析(principal component analysis，PCA)、偏最小二乘判别分析(partial least squares-discriminant analysis，PLSDA)与平行因子分析(parallel factor analysis)等[3]。然而，这些降维方法均未将纵向组学数据集的时间顺序信息纳入模型，即打乱时间顺序后仍然能得到相同的结果，且并不适用于非线性组学数据[13]。目前，已开发的降维方法主要包括基于多水平思想的线性降维方法及基于核函数的非线性降维方法。

(1)线性降维方法

纵向数据具有多水平结构资料的特征，观察单位为1水平单位，该观察单位的重复测量资料为2水平单位。多水平模型的核心思想是通过估计两个水平上的方差，并考虑解释变量对方差的影响，充分利用各水平内的聚集信息，从而获得回归系数的有效估计，提供正确的标准误与置信区间[14-15]。

多水平同步成分分析(multilevel simultaneous component analysis，MSCA) 是结合多水平思想与主成分分析思想的降维方法[16-17]。多水平同步成分分析模型将数据集总变异分为个体间和个体内两个水平上的变异。在相同的成分数下，PCA与MSCA相比，解释的变异相同或更多，对MSCA施加限制越多则解释变异越小。但MSCA相较于PCA的可解释度更好，其中不同的亚模型能够解释数据中不同的变异，其个体内模型比PCA能更好地展示数据中的动态变异，而个体间模型又比PCA更好地展示个体间的非动态变异。

多水平偏最小二乘判别分析(multilevel PLS-DA，ML-PLS-DA) 的核心思想是将个体间和个体内两水平的变异分开解释[18-19]。数据分析时，首先将个体间变异和个体内变异的部分分开，其中个体间变异是对个体两次测量的均值分析得到，而个体内变异是对个体前后两次测量的差值进行分析。当使用ML-PLS-DA来描述个体内变异时，主要是关注个体间相同的处理效应。因此，ML-PLS-DA的第一主成分描述主要效应，其后的成分描述个体间不同的处理效应。

(2)非线性降维方法

线性降维方法计算简便，原理简单，易于解释。但该类方法在处理非线性组学数据时，仍然存在一定局限性。为更精确挖掘非线性组学数据信息，研究者在传统降维分析方法中引入非线性。其中，应用最广泛的是基于核函数的主成分方法(kernel principal component analysis)[20]，核主成分分析方法将原始数据空间RM中的样本x映射至特征空间F(Φ：RM→F；x→X)，在特征空间内对样本X实现主成分分析[20-21]。该方法较传统主成分分析方法有以下优点[22]：① 引入了非线性映射函数Φ，将原始数据映射至特征空间，能够更好地解释原始数据中非线性变异部分；②可使用不同核函数，对不同种类非线性组学数据实现降维；③能提供比主成分分析更多的特征数目，可以最大限度地提取特征信息。与核主成分分析类似，核偏最小二乘判别分析(kernel partial least squares-discriminant analysis)也是利用核函数方法将原始数据映射至特征空间，以描述特征间的非线性关系[23]。除基于核函数的分析方法外，非线性降维方法还包括局部线性嵌入、等距映射、多尺度变换等流形学习方法。

纵向组学数据统计分析策略

纵向组学研究设计在成为研究生命体功能变化有力手段的同时，也给统计分析带来了新的机遇与挑战。研究者们在进行纵向组学数据分析过程中，常常忽略了数据集的时序性及相应统计分析方法原理与前提假设，降低了研究结论的可靠性。本文针对纵向组学数据特点，探索了组学统计分析策略，具体总结如图1所示。

高通量测量技术中的实验环境、仪器性能及人工操作等均会对数据质量产生影响。因此，组学测量数据变异来源广泛，除生物变异外，还包括环境影响及测量误差等。目前常用数据预处理方法包括噪声滤除、基线校正及标准化处理。

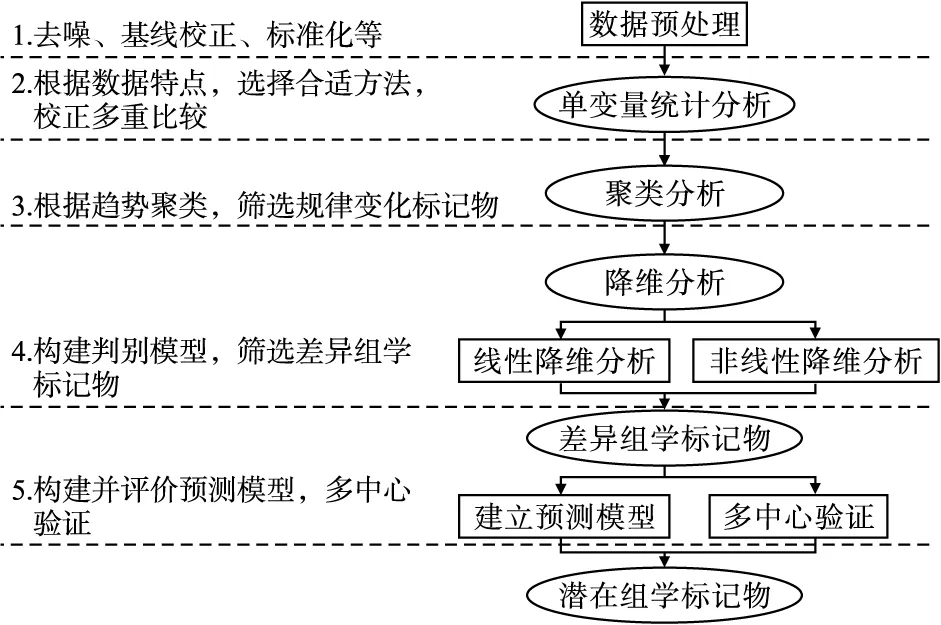
图1 纵向组学数据统计分析策略流程图

单变量统计分析思想简单，易于理解，常用于快速筛选组学研究中随时间动态变化的组学标记物[24-25]。在单变量统计分析过程中，重复测量方差分析对数据资料要求极为严格，须同时满足方差分析条件及协方差阵球对称性，混合效应模型及广义估计方程能考虑到纵向数据的相关性，处理缺失值问题，但后者无法处理高维纵向数据的非平衡性问题，存在一定局限性。此外，高维情境常涉及多重比较问题，需着重考虑对假设检验的检验水准α进行校正，目前常用校正方法包括Bonferroni校正法及FDR(false discovery rate) 校正法[26-27]。

聚类方法常用于组学标记物时序变化趋势分析。在经单变量分析后，可通过聚类算法筛选出规律变化的不同类组学标记物，对不同类的组学标记物选择不同的模型进行研究。K均值聚类算法计算简便快捷，适应性广，但在聚类过程中未考虑到纵向数据的时间序列信息；有序样品聚类大多用于样品聚类，是一种特殊条件系统聚类算法，但难以直接得出相关序列特征的结论；模糊聚类算法用于时间序列数据时，以时间为维度，计算隶属度，同时允许了数据性质的模糊性，为数据结构的描述提供了详细的信息。

主成分分析与偏最小二乘法判别分析是组学研究中常用的降维方法。线性降维方法计算简便，原理简单，易于解释。在降维的同时，考虑到数据的时序信息，能更好地展示数据集的动态变异。非线性降维方法在降维分析中进一步引入非线性，更精确构建判别模型，挖掘非线性数据信息。最终，使用外部测试集评价潜在组学标记物预测效果，探索潜在组学标记物的生物学功能，为分析结果提供合理的生物学解释。

由于纵向组学数据的复杂特性，上述分析手段能在一定程度上解决组学数据统计分析问题，但仍存在局限性。目前组学标记物变量筛选的方法主要依靠单变量统计分析及后续改进的偏最小二乘法判别分析等方法。数据发生轻微变化时，变量筛选效果也会受到影响，因此建立稳定有效的纵向高维数据变量筛选方法仍然值得研究者们进行探讨[28]。此外，利用纵向组学数据进行因果推断分析时，如何校正时依混杂因素对因果效应估计的影响也需要进一步研究[29-30]。以上两个关键科学问题的解决将会对纵向组学数据提供新的思路与契机。