MMPC-Tabu混合算法的贝叶斯网络模型在高脂血症相关因素研究中的应用*

王旭春 宋伟梅，2 潘金花 任 浩 张 壮 翟梦梦 陈利民 仇丽霞△

【提 要】 目的 本研究采用MMPC-Tabu混合算法构建山西省高脂血症的贝叶斯网络模型，研究高脂血症及其相关因素间的网络关系及相关程度，并通过贝叶斯网络对高脂血症进行患病风险推理，为慢病影响因素分析提供更合理的建模方法。方法 采用logistic回归对山西省18岁以上居民高脂血症的调查数据进行变量初步筛选，再以MMPC-Tabu混合算法和极大似然估计法构建贝叶斯网络。结果 2013年山西省高脂血症患病率为42.6%(95%CI：41.1%～44.1%)。将logistic回归初筛与高脂血症有关的9个变量，采用MMPC-Tabu算法构建高脂血症的贝叶斯网络模型，结果显示：中心性肥胖和BMI与高脂血症直接相关，是高脂血症的父节点，即它们与高脂血症的发生有关；高血压、身体活动、性别、年龄、地区、糖尿病通过影响中心性肥胖和BMI间接影响高脂血症的发生。结论 贝叶斯网络可以反映因素与疾病整体联动效应，揭示高脂血症直接和间接相关的因素和关联强度，同时阐明除高脂血症以外的其他影响因素间的关系，可为慢性病与相关因素的研究提供合理的方法。

近年来，随着经济的迅猛发展，居民生活水平及饮食习惯的改变，血脂异常率不断上升，2014年中国血脂异常率已高达41.9%[1-2]。血脂升高导致血管粥样硬化，是促进心脑血管疾病发生和发展的关键因素[3]。因此，对高脂血症的相关因素进行全面分析，揭示因素间复杂的网络联系，有针对性地对高脂血症采取预防控制措施显得尤为重要。

目前，国内外对高脂血症的相关因素研究多采用logistic回归，以优势比(odds ratio，OR)的大小来反映相关因素对高脂血症的影响强度。在实际应用中，logistic回归的变量独立性假设很难得到满足，且无法区分高脂血症的直接或间接相关因素。从医学生物学角度分析，疾病与病因以及病因之间都可能存在着复杂的网络联系，各变量间相互影响，具有整体联动性，这在传统logistic回归中难以体现。而贝叶斯网络不仅对变量间的独立性没有严格要求，还可以通过网络图和条件概率表来反映因素间的复杂联动关系及相关程度[4]。另外，在已知某些节点(影响因素)状态的情况下，贝叶斯网络还可以利用贝叶斯定理对未知节点(高脂血症)进行风险推理，弥补了logistic回归在进行概率预测时需要掌握所有因素状态的不足[5-6]。相比于logistic回归，贝叶斯网络能更为直观地揭示疾病与病因之间复杂联动的网络风险机制，是描述疾病及其影响因素间相关关系的有效方法[7-8]。

贝叶斯网络的结构学习算法[9]包括基于约束的算法、基于评分搜索的算法以及二者结合的混合算法，约束算法能得到全局最优解，且学习效率较高，但高阶条件独立性检验计算复杂且所得结果也不够可靠。评分搜索算法虽然能弥补前者的一些不足，但易陷入局部最优。因此，有研究者提出了将两者相结合的混合算法，比较经典且应用较为广泛的混合算法为Tsamardino等[10]于2006年提出的最大最小爬山(max-min hill-climbing，MMHC)混合算法，该算法结合了最大最小父子集(max-min parents and children，MMPC)算法和爬山法，但爬山法容易陷入局部最优。2015年，课题组成员张雪雷[11]证实了作为全局智能优化算法的禁忌搜索算法(Tabu search algorithm，Tabu)对贝叶斯网络优化效果优于爬山算法。课题组前期尝试将MMPC算法与Tabu算法进行结合，建立MMPC-Tabu混合算法，并通过仿真实验证实了在节点数较多、大样本的情况下，MMPC-Tabu算法构建贝叶斯网络的效果优于MMHC算法。

本研究利用山西省2013年高脂血症及其危险因素监测数据进行分析。首先利用logistic回归初筛变量，找出主要变量；然后基于MMPC-Tabu混合算法构建高脂血症及其相关因素的贝叶斯网络，探究高脂血症及其影响因素间的网络结构关系，为慢性病相关因素的研究提供新的网络构建方法。

资料与方法

1.调查对象

本研究按照国家慢病调查方案，根据山西的地理位置划分为8个大片区，采用多阶段随机抽样方法收集样本。首先在每一个大片区随机抽取1个区(县)作为国家慢病监测点，随后在各个监测点随机抽取4个乡镇、街道或团，在已抽取的乡镇、街道或团中随机抽取3个村、居委会或连，再在抽取的村、居委会或连中随机抽取50户居民，按照KISH表法在每户居民中随机抽取1位居民(18岁及以上)。

纳入标准：调查前在调查点内居住时间超过6个月、年龄≥18岁的居民。排除标准：居住在功能区(工棚、军队、学生宿舍、养老院等)内的居民。伦理审查编号为201307。

2.数据收集

采用问卷调查、身体测量、实验室检查等方法获取所需样本资料。

3.评价标准

(1)高脂血症：依据《中国成人血脂异常防治指南》[12]中的血脂异常诊断标准；(2)高血压：依据《中国高血压防治指南》[13]中高血压评价指标；(3)糖尿病：指空腹血糖大于等于7mmol/L或2小时餐后血糖大于等于11.1mmol/L，或已被诊断为糖尿病的人；(4)吸烟：指连续6个月日均吸烟量大于等于1支者；(5)身体质量指数BMI低于18.5kg/m2为偏瘦、正常体重在18.5至23.9kg/m2之间、24.0至27.9kg/m2为超重、大于等于28.0kg/m2为肥胖；(6)中心性肥胖：指女性腰围大于等于80 cm，男性腰围大于等于85 cm；(7)心率：心率低于60次/min为心动过缓、高于100次/min为心动过速、60至100次/min为正常范围；(8)身体活动度：以代谢当量的25%和75%为界，将身体活动度分为身体活动不足、达标和充足。

4.统计学处理

采用IBM SPSS 22.0进行统计描述和多因素logistic回归。利用R 3.5.0中bnlearn package进行贝叶斯网络结构学习，bnlearn package包含多种贝叶斯网络学习算法，本文采用MMPC和Tabu结合的混合学习算法。采用Netica可视化贝叶斯网络，建立推理模型并计算条件概率。Netica是用Java开发的贝叶斯网络学习工具，能够高效地建立贝叶斯网络拓扑结构，并可根据先验知识及更新的知识进行传递和积累，适用性强，可视化操作方便。先验概率分为基于历史资料获得的客观先验概率和根据主观经验判断得到的主观先验概率，本文采用客观先验概率，极大似然法估计条件概率。

5.MMPC-Tabu混合算法概述

MMPC-Tabu结构学习算法分为两个阶段，第一阶段采用MMPC[14]算法获得贝叶斯网络框架；第二阶段利用禁忌搜索算法确定网络边及其方向，建立完整的贝叶斯网络结构。

MMPC算法为基于约束的启发式算法，也分为两个阶段：(1)采用Max-Min启发式搜索方法获得每个节点的候选父子节点集(candidate parents and children，CPC)，同样利用该搜索方法计算其余所有变量与目标变量T之间的最小关联度值，从中选择关联度最大的一个变量进入CPC，在CPC中全部子集都给定的条件下，若其他节点都独立于T，该阶段结束；(2)通过条件独立性测试函数Ind(X；T|Z)移去CPC中第一阶段误入的变量。若CPC中存在X，使Ind(X；T|Z)成立，其中Z∈CPC，即变量X与目标变量T在已知Z时具备独立性关系，则将X移出CPC。

禁忌搜索算法[15](Tabu算法)模拟人类大脑的短期记忆功能进行搜索，属于全局智能优化的搜索算法，具有参数少、结构简单和全局寻优能力强等特点。在网络框架中，执行加边、删边、逆向边操作，通过禁忌表和局部邻域移动机制来避免重复搜索，以此加快搜索进程，并利用藐视准则来激活那些被纳入禁忌表的优良状态，通过在多邻域方向进行有效探索，使搜索范围跳出局部最优，最终得到全局的最优解。

MMPC- Tabu混合算法结合了MMPC算法和禁忌搜索算法，与经典的MMHC算法相比，MMPC- Tabu算法在搜索阶段进行了改进，采用禁忌搜索使得搜索过程跳出了局部最优，弥补了MMHC算法搜索阶段的不足。

结 果

1.人群基本特征及血脂异常率

本研究共调查4776人，资料整理后保留完整数据4105例，保留可能与高脂血症发生相关的17个变量，变量及其赋值详见表1。

2.高脂血症多因素logistic回归

采用logistic逐步回归对原始数据所保留的17个变量进行变量筛选，其中α入取0.10、α出取0.15，确定显著相关因素，以简化后期的贝叶斯网络模型。

多因素logistic逐步回归的分析结果显示：性别、地区、身体活动度、BMI、中心性肥胖、高血压和糖尿病7个变量与高脂血症显著相关。男性患高脂血症的风险相比于女性升高了38.3%；农村居民患高脂血症的风险相比于城市居民升高了15.2%；BMI每增加一个等级，患高脂血症的风险增加47.1%；中心性肥胖者患高脂血症的风险较非中心性肥胖者增加70.2%，身体活动度每增加一个等级高脂血症的患病风险降低11.5%，合并糖尿病和高血压者患高脂血症的风险相比于血糖、血压正常者，分别升高了30.7%和26.7%，详见表2。

3.高脂血症的影响因素间的关联性分析

logistic回归在基于变量独立的前提假设下，可以找出与高脂血症显著相关的独立影响因素，但一般情况下，各影响因素间往往相互关联，由表3、4中不同年龄、性别与BMI、中心性肥胖和身体活动度的相关分析以及高血压、糖尿病与高脂血症其他影响因素间的差异性检验可知，年龄、性别与BMI、身体活动度和中心性肥胖有关(P<0.05)；BMI、中心性肥胖、年龄、地区等因素均与高血压、糖尿病相关(P<0.05)，身体活动度与高血压之间的差异也存在统计学意义。说明高脂血症的影响因素间并不互相独立，且存在复杂的网络联系。

表1 变量赋值及构成比

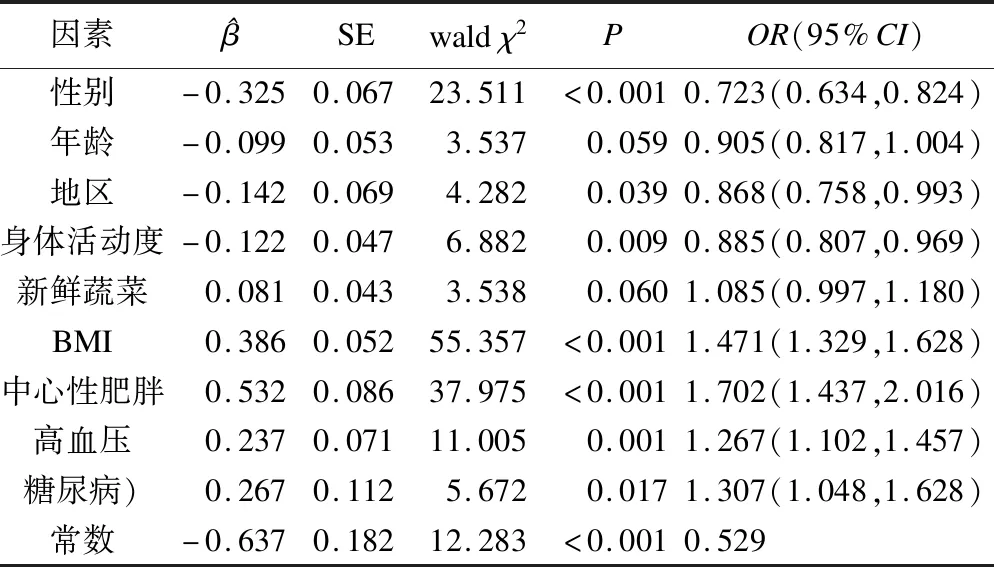
表2 高脂血症的logistic回归分析

表3 不同年龄、性别与BMI、中心性肥胖和身体活动度的关系

表4 高血压、糖尿病与高脂血症其他影响因素的关系

4.高脂血症的贝叶斯网络模型

将logistic回归中以α入取0.10、α出取0.15为准筛选的9个变量，采用MMPC-Tabu混合算法和极大似然估计法构建高脂血症及其相关因素的贝叶斯网络和条件概率表(图1)。图中节点方框中的数值与矩阵条代表的是各节点的先验概率，例如高脂血症的患病组对应数值为42.6，表示患高脂血症者在全部人群中所占比例为42.6%，为该节点的先验概率。有向弧表示变量间的条件依赖关系。由图可知，中心性肥胖和BMI与高脂血症直接相关，为高脂血症的父节点，直接影响着血脂的变化，高血压、身体活动、性别、年龄、地区、糖尿病通过影响中心性肥胖和BMI与高脂血症间接相关。

贝叶斯网络还可以描述性别、年龄、地区、身体活动、高血压、糖尿病这些除高脂血症之外的影响因素间存在着的复杂网络关系。如贝叶斯网络提示高血压与BMI、年龄、地区有关，在表2中也显示随着BMI值、年龄的增加，高血压的检出率随之增加，农村居民的高血压患病率高于城市居民；年龄和性别与身体活动度之间直接相关，且通过网络间接影响BMI和中心性肥胖，这与表3中显示的不同年龄、性别与BMI、中心性肥胖和身体活动度有关的结论相一致。充分说明贝叶斯网络能很好地揭示疾病与病因，以及病因之间复杂的网络联系。

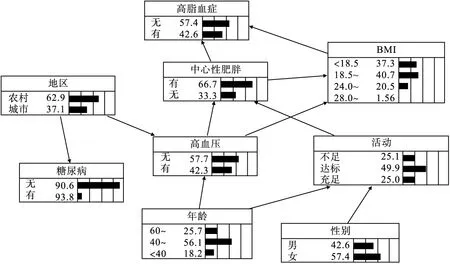
图1 最大最小父子集——禁忌搜索混合算法构建高脂血症贝叶斯网络及先验概率

5.高脂血症的风险推理

表5是高脂血症节点的条件概率分布表，可以看出高脂血症与其两个父节点中心性肥胖和BMI之间的概率依赖关系。当某人BMI在正常范围(18.5～24.0kg/m2)且体型正常时，其患高血脂的风险为0.26416；当其体型正常，BMI>28.0kg/m2时，患高血脂的风险提高到0.41736；而当其属于中心性肥胖且BMI>28.0kg/m2时，其发生风险提高到了0.57315。

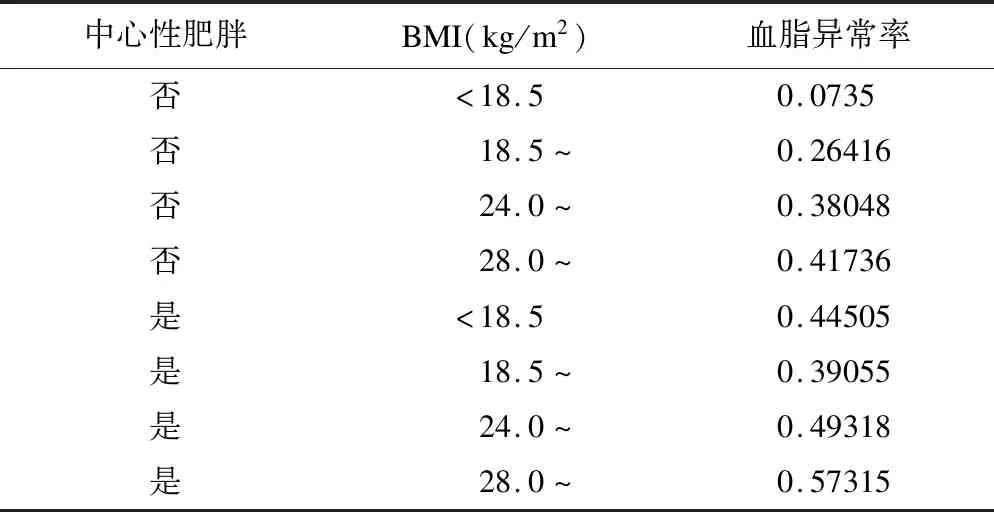
表5 高血脂症节点的条件概率表

贝叶斯网络还可以进行因果推理，即根据已知节点的信息对未知节点进行概率预测，继而对高脂血症进行风险推理。若已知某人为中心性肥胖而无其他病史，通过贝叶斯网络推理可知，其患高脂血症的可能性为0.498(图2)；若其仅患有高血压，患高脂血症的可能性为0.461(图3)；如果该个体在中心性肥胖的基础上还患有高血压，则患高脂血症的可能性增加到0.508(图4)。

讨 论

贝叶斯网络也被称为概率图模型，是依据概率值进行不确定性推理的方法，通过构建网络图的形式反映多个变量间相互联系，以条件概率的形式反映变量间的关联强度，能直观地展现高脂血症及其相关因素间复杂的网络关系。贝叶斯网络提示，中心性肥胖和BMI与高脂血症直接相关，是高脂血症的父节点，直接影响着血脂的变化，其中高血压、身体活动、性别、年龄、地区、糖尿病通过影响中心性肥胖和BMI间接对血脂产生影响。这些研究结果与现有的医学知识相符。因此，适度锻炼、注意控制体重和腰围，可以降低高脂血症的风险，在此基础上也可以降低高血压的风险。由此可见，贝叶斯网络可以很好地刻画各因素间、因素与高脂血症间复杂的网络关系，可以识别与高脂血症直接相关和间接相关的因素，对于断面调查数据可以给出因果关系的提示，便于全面深入发掘因素间的内部关系，能主次分明地提出高脂血症的预防策略。同时，由于贝叶斯网络研究变量间的关系时，没有输入和输出变量，因此，它还可以描述其他因素间的关系。这些是logistic回归分析所不能达到的。

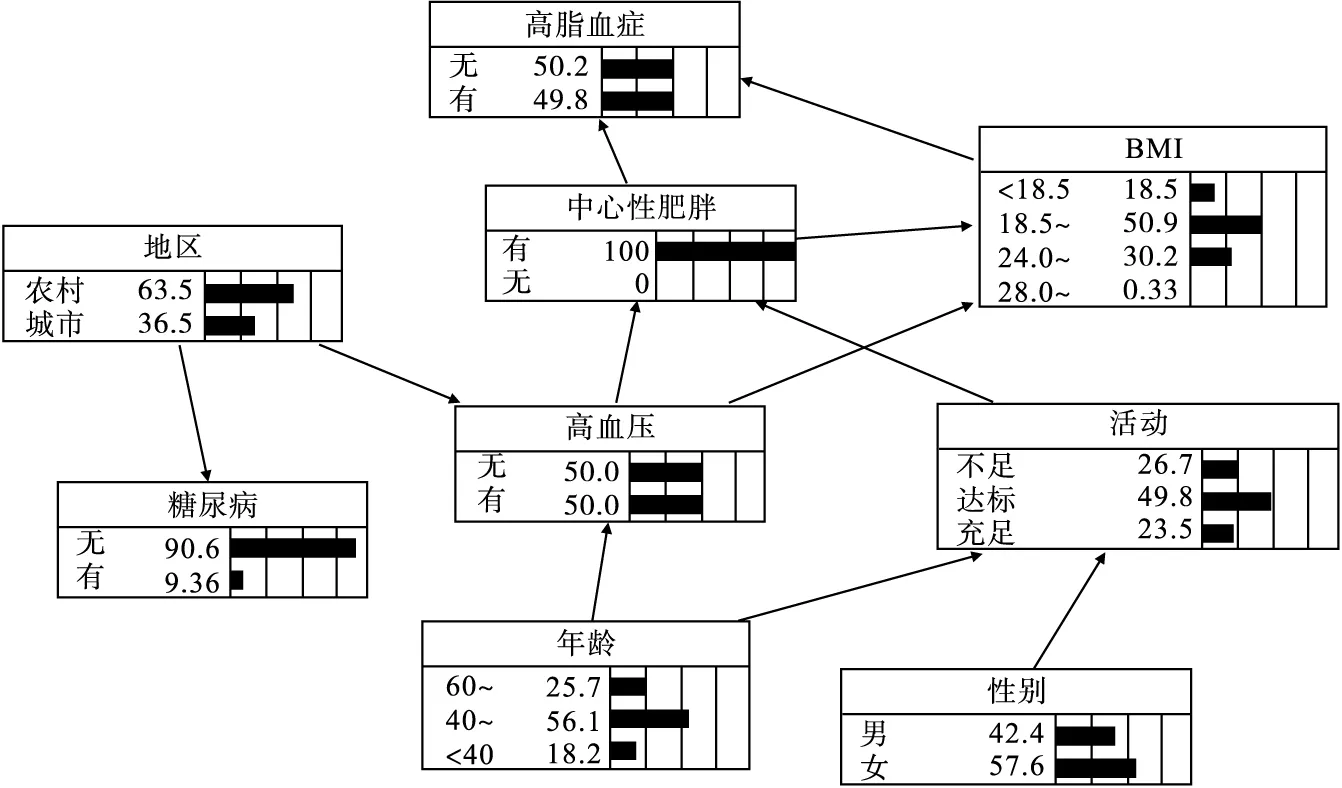
图2 中心性肥胖时血脂异常的风险推理

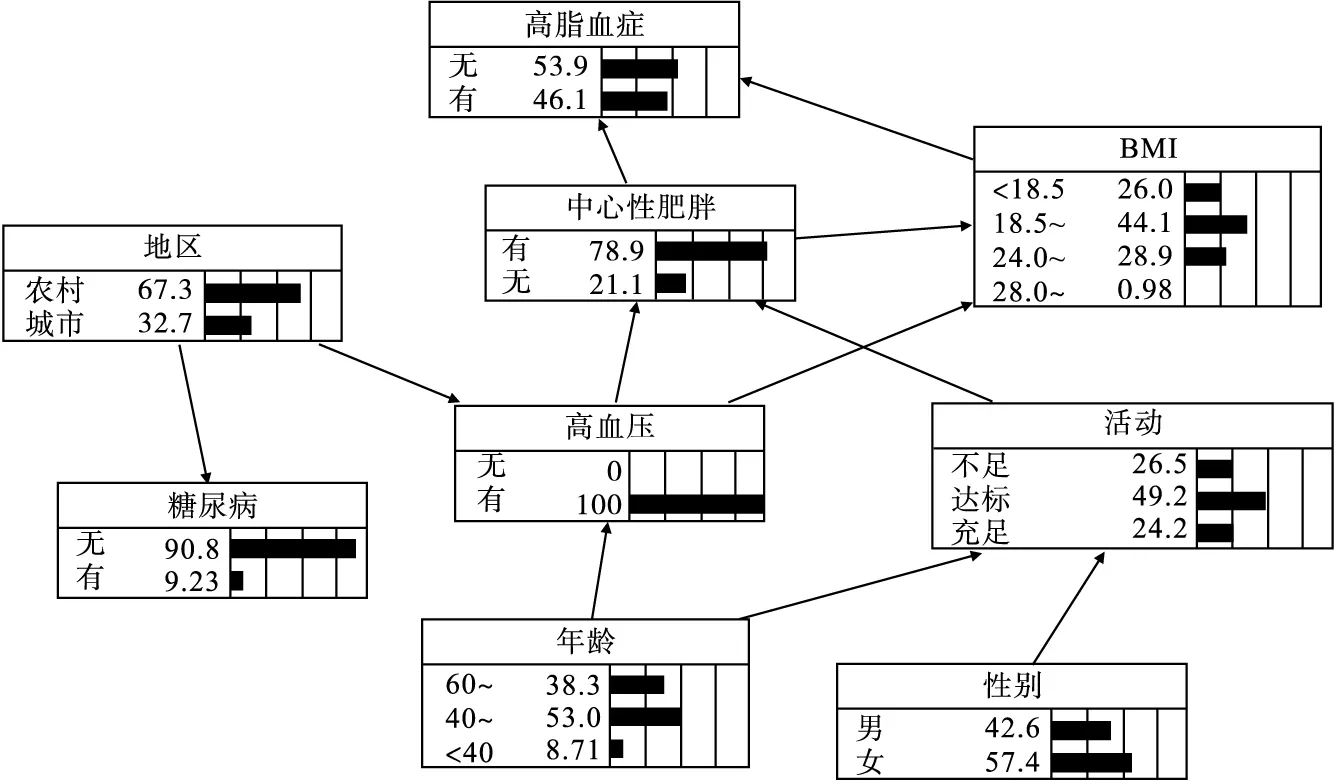
图3 患高血压时患高脂血症的风险推理

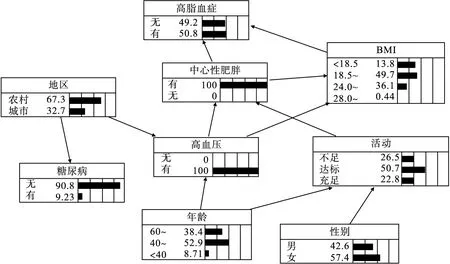
图4 患高血压且为中心性肥胖时患高脂血症的风险推理

贝叶斯网络还能根据已知节点的状态来推断未知节点的概率，从而对高脂血症进行风险推理。某个体患高脂血症的先验概率为P高脂血症=0.426，若某个体患有高血压，其患高脂血症的可能性为P(高脂血症|高血压)=0.461，风险提高了3.5%；如果患有高血压的同时还属于中心性肥胖，则患高脂血症的可能性变为P(高脂血症|高血压，中心性肥胖)=0.508，风险进一步提高了8.2%。由此可见，贝叶斯网络可以进行序贯推理，根据某因素条件概率的变化，评价该因素的风险强度，说明其在预防工作中的价值；另外，从风险推理的过程中也能看到，若某一因素变化，网络中其他因素不同水平的条件概率随之发生改变，体现了事物的整体联动性，换句话说，贝叶斯网络反映因素与疾病的整体联动性，并不区分主效应或交互效应，更能客观、全面地描述因素与疾病的关联强度。而logistic回归是不能进行序贯推理的，也不能反映因素与疾病的整体联动性。

由于贝叶斯网络建模时对样本量的需求较大，同时对构建过于复杂的网络结构不太适用，只要抓住主要的因素就达到了研究目的。因此，实际工作中，可以先采用logistic回归分析对变量进行初筛，再构建贝叶斯网络，以深入地描述变量间的关系。

综上所述，本课题基于MMPC-Tabu算法构建的高脂血症贝叶斯网络可以合理地描述高脂血症与各变量间的关系，该算法构建的慢性病贝叶斯网络的研究成果尚未见报道。因此，本课题将为慢性病与相关因素的研究提供更合理的方法。