观察性研究中三种控制混杂偏倚的匹配方法比较*
2022-09-14陈文松刘玉秀许敏怡巩浩雯李维勤
陈文松 刘 曼 刘玉秀,4△ 许敏怡 熊 殷 巩浩雯 李维勤
【提 要】 目的 探讨观察性研究中用于混杂偏倚控制的倾向性评分匹配、马氏距离匹配和遗传匹配三种方法的性能。方法 针对连续型结局变量,设定混杂变量与处理分组变量之间具有不同复杂度的回归模型结构,采用Monte-Carlo模拟方法比较三种匹配方法在处理组间效应估计和匹配前后自变量均衡的区别,进而对三种方法性能进行评估。结果 在给定的模拟情形下,相比于倾向性评分匹配和马氏距离匹配,遗传匹配法得出的效应估计偏差最小,匹配后两组自变量均衡性最好。结论 遗传匹配在三种匹配方法中表现出较好的统计性能,可考虑作为观察性研究中控制混杂偏倚优先推荐的匹配方法。
在非随机观察性研究中,当需要考虑某目标处理变量的效应时,由于混杂偏倚的客观存在,常常导致估计出的组间差别不能反映真实情况,此时混杂偏倚的控制就尤为关键。除已知的分层分析、多因素分析等传统方法,近年来,利用距离度量(metric)对研究个体进行匹配的倾向性评分匹配法(propensity score matching,PSM)以及马氏距离匹配法(Mahalanobis distance matching,MDM)、遗传匹配法(genetic matching,GM)在医学研究中的应用越来越广泛[1-3],然而有关这几种匹配方法在统计推断时的性能比较研究尚未见详细文献报道。
本文将在介绍基于进化算法的遗传匹配方法的基础上,采用Monte-Carlo模拟方法对三种匹配方法的统计性能进行比较研究,并通过一个实例进行分析说明。
匹配方法
理论上,将同质性相近的个体在不同的组间进行匹配,组间的自变量的分布将趋于均衡,从而减少或抵消两组混杂因素对治疗效果的影响,这就是匹配的基本原理[4-5]。在医学研究中,除规定匹配个体所有变量取值均相同的精确匹配外,以马氏距离为基础的多元变量匹配和将多维数据转化为一维的倾向性评分匹配最为常见。有关倾向评分匹配已有较多文献介绍,此不赘述。以下重点介绍基于马氏距离发展的广义马氏距离,以及以广义马氏距离为度量的遗传匹配。
1936年,P.C.Mahalanobis提出了马氏距离(Mahalanobis distance,MD),用以表示数据的协方差距离[6]:
(1)
其中Xi和Xj分别为第i个个体和第j个个体的自变量组成的向量,S-1为样本协方差矩阵的逆。个体间马氏距离越小,表示个体间越相似。
2013年,Diamond及其同事提出了基于进化算法的遗传匹配(genetic matching)来控制组间混杂因素的影响。遗传匹配在马氏距离的基础上创立了更一般化的距离度量,即广义马氏距离(generalized Mahalanobis distance,GMD)[7]:
(2)
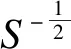
个体的自变量集合X除自变量以外,还可以包含倾向性评分。此时方程(1)中的X可以用Z代替,其中Z是一个由倾向性评分π(X)和自变量X组成的矩阵。如果将PS以外的其他变量的权重设为0,此时GMD等同于倾向性评分;如果将PS的权重设为0,其他自变量的各个权重设为1,此时GMD等价于马氏距离。PSM和MDM都是遗传匹配的极限情况。
常见的计算倾向性评分的方法有logistic回归、Probit回归,以及机器学习估计中的神经网络、支持向量机、分类与回归树、随机森林等方法[8-9]。其中利用logistic回归计算倾向性评分最为常见,即利用组别为因变量,建立logistic模型,本文就采用这种方法计算倾向性评分。
遗传匹配根据每个变量的相对重要性对其加权来获取最佳的自变量平衡。遗传匹配利用遗传算法(genetic algorithms)搜索一系列距离度量,通过最小化损失函数,找到使得自变量均衡性最高的加权矩阵W。该算法允许使用者自定义损失函数,默认损失函数定义为匹配后两组自变量的Kolmogorov-Smirnov检验的P值及配对t检验的P值最小值,用以描述两组自变量的最大差异。
遗传算法是一种通过模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程搜索最优解的方法[10-11]。图1总结了遗传算法的流程。该算法产生一批初代权重Ws,每个W对应一个不同的距离度量。在每一代中,计算每个匹配样本对应的损失函数。选择使得损失函数最小的权重作为父代,产生子代权重并不断迭代这一流程,直至渐进收敛于最优解。每一代产生的权重数量称为种群规模,在迭代过程中种群规模保持不变。增大种群规模通常会改善遗传匹配的效果,但会增加算法寻找最优解所花费的时间。
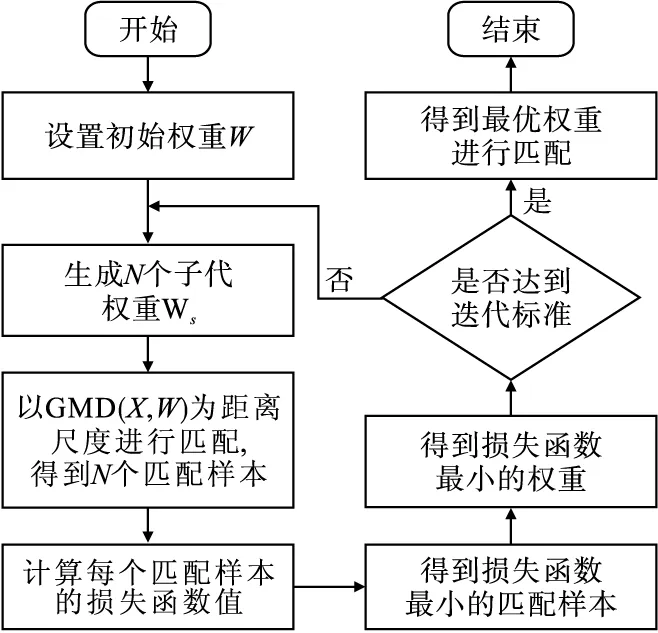
图1 遗传算法流程图
当损失函数满足迭代标准时停止迭代,此时的权重即为最优权重。利用最优权重计算广义马氏距离,根据此距离度量进行匹配,得到匹配后样本。与倾向性评分一样,此时可以使用不同的匹配策略,例如有无替换、有无卡钳的最近邻匹配或最优匹配等。
值得注意的是,遗传匹配与其他匹配方法的使用前提一样,即要事先确定匹配的具体变量、选定测量自变量平衡性的指标,以及指定合适的匹配方式。
模拟实验
本模拟实验基于模拟生成的数据集,采用Monte-Carlo方法比较遗传匹配与经典的马氏距离匹配、倾向评分匹配在倾向性评分模型不同复杂程度下的效应估计精度和匹配前后自变量均衡程度,评价其统计性能,为方法学选择提供理论依据。
1.模拟数据
Setoguchi及其同事在探究机器学习技术构建倾向性评分模型的研究中提出了一种模拟数据生成策略[12],该策略产生的模拟数据包含了实际中可能出现的多数情景,具有较好的代表性。本研究在此策略的基础上进行了略微的修改。利用SAS软件总共生成1000个模拟数据集,其中每个数据集的样本量为1000。在每个数据集中,模拟生成10个自变量,其中4个混杂变量,3个暴露预测变量和3个结果预测变量。4个自变量(X2,X4,X7,X10)服从标准正态分布,其余6个二元变量(X1,X3,X5,X6,X8,X9)则由标准正态分布转换得到,具体的模拟数据变量结构及自变量间相关系数见图2。设定group为组别变量,并使其在自变量均值上约等于0.5以保证两组人数相同。Y作为连续型结局变量,由group和其他自变量的线性组合生成。在文后附录中提供了计算倾向性评分、结局生成及治疗分配的详细过程。

图2 模拟数据各变量关系的基本结构
基于所设定的模拟数据结构,本研究指定了7种复杂程度各不相同的情形来指代真正的倾向性模型,以便评估三种匹配方法在倾向性模型不同复杂程度下的表现情况:
A:线性可加(仅主效应)
B:轻微非线性(包含1个二次项)
C:中等非线性(包含3个二次项)
D:轻微非可加性(包含3个两因素交互作用项)
E:轻微非可加性和非线性(包含3个两因素交互作用项和1个二次项)
F:中等非可加性(包含10个两因素交互作用项)
G:中等非可加性和非线性(包含10个两因素交互作用项和3个二次项)
为评价模拟生成的数据集的统计特征,本研究比较了两组间自变量的均衡性。图3展示了倾向性评分模型为情形A时两组间倾向性评分分布与自变量均衡情况,其他情形下的模拟数据表现与其类似,这里不予罗列。从图3可知,试验组中倾向性评分大于0.5,对照组中倾向性评分小于0.5,两组倾向性评分分布互有重叠;两组间混杂变量与暴露预测变量的标准化差值大于0.1,混杂变量与暴露预测变量在两组间分布不均衡。

图3 情形A时模拟数据集两组自变量均衡性
2.匹配方案
本研究使用MDM、PSM和GM来估计每个情形中的group的效应。匹配方案均选择有放回的最近邻匹配(nearest neighbor matching),匹配比例为1:1,同时PSM的卡钳值设为0.02,GM中每代的种群规模(pop.size)设置为500。由于实际数据的复杂性,本研究很难确定哪些变量应纳入模型以及模型中变量间的具体关系,所以在PSM和GM计算倾向性评分时,采用两种策略建立倾向性评分模型:在第一种策略中,默认所有自变量均以线性可加的形式包含在倾向性评分模型中;而在第二种策略中,仍旧将所有自变量纳入倾向性评分模型,但对于连续型变量,使用限制性立方样条(restricted cubic spline,RCS)来考虑连续型变量的非线性关系。MDM使用所有自变量计算马氏距离。三种匹配方法均应用R软件中的Matching包实现。此外,本研究还在遗传匹配中去除倾向性评分,只使用所有自变量,探究其对结果的影响。其中,使用“PSM”表示使用线性可加模型进行的倾向性评分匹配,“PSM+”表示使用非线性可加模型进行的倾向性评分匹配,“MDM”表示马氏距离匹配,“GM”表示使用线性可加模型得到的ps进行的遗传匹配,“GM-”表示不使用ps进行的遗传匹配,“GM+”表示使用非线性可加模型得到的ps进行的遗传匹配。
3.评价指标
考虑采用2个度量值作为效应估计性能的评价指标,分别为:①相对偏倚(average percent relative bias,APRB):估计值与真实值的相对差异百分比;其中采用配对t检验对匹配后样本计算估计值。②均方根误差(root mean squared error,RMSE):估计值与真实值偏差的平方与估计次数比值的平方根。另外,采用2个指标来评价匹配前后自变量均衡性,分别为:①标准化差值(standardized mean difference,SMD):用于定量评价均衡性。一般认为标准化差值小于0.1时具有良好的均衡性。②配对t检验或配对卡方检验的P值。对于连续性变量使用配对t检验,对于分类变量使用配对卡方检验。考虑到篇幅所限,本文中自变量均衡性结果仅提供标准化差值。
4.模拟结果
在不同的倾向性评分模型下,使用不同方法对模拟数据集分析,比较不同方法的效应估计性能评价指标和匹配前后自变量均衡性。
(1)不同匹配方法后的处理效应估计的比较
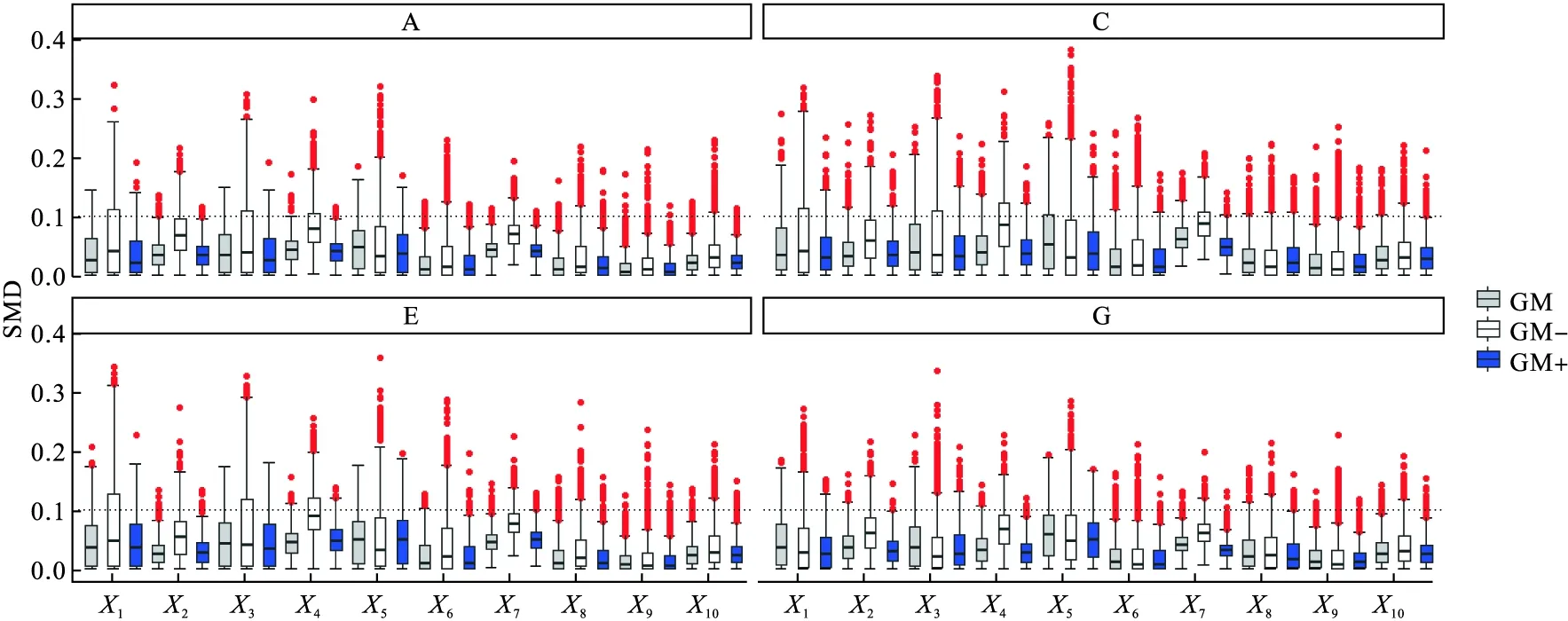
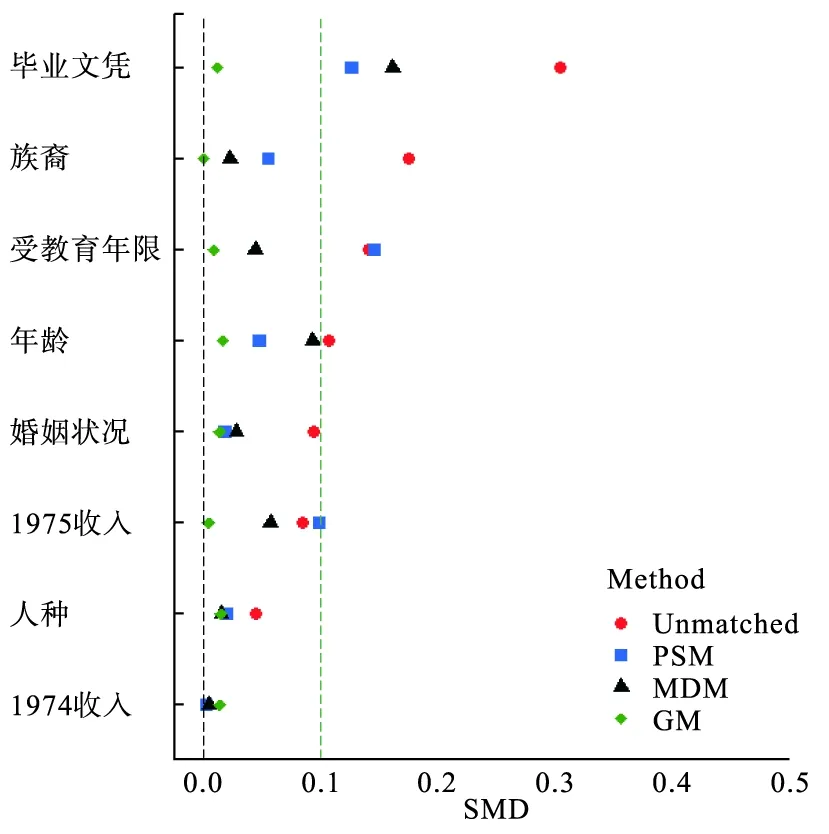
从表1可见,各方法在各情形下的总体偏倚从小到大依次为:GM≈GM+ 表1 不同匹配方法效应估计相对偏倚的比较 (2)不同匹配方法后组间自变量的均衡性比较 考虑结果的呈现性,本研究在此挑选了7种情形中的具有代表性的4种情形,并选择了各类匹配方法中表现最优的3种方法。从图4可见,经遗传匹配处理后,两组自变量的标准化差值最小,在各种情形中的自变量均衡情况表现均最优。在指定了正确的倾向性评分模型后(即情形A),PSM+与GM在整体上表现相近,但其SMD的分布略高于GM。随着真实倾向性评分模型复杂度的增加,PSM+的两组自变量均衡程度开始下降。MDM在控制分类变量的均衡性上表现较优,但在连续型变量上表现最差,其中在匹配前最不均衡的变量X7上控制表现最差。 图4 三种匹配方法匹配各自变量均衡性情况:SMD (3)倾向性评分匹配中不同建模策略对统计性能的影响 图5给出了在不同的真实倾向性评分模型下,使用两种不同建模策略进行倾向性评分匹配的自变量均衡情况。从图5可见,使用非线性可加模型进行倾向性评分匹配的组间自变量均衡程度更优,在任何情形下各变量SMD的上四分位数均小于0.1。当真实倾向性模型仅为简单的线性可加模型时(情形A),PSM与PSM+的表现一致;当真实倾向性模型包含非线性项时(情形C、情形E、情形G),在二元变量上,PSM与PSM+的表现一致。但在连续型变量上,PSM+的表现优于PSM。从表1可见,在任何情形下,PSM+的疗效相对偏倚小于PSM。 (4)遗传匹配中使用倾向性评分与否对统计性能的影响 图6给出了在不同的真实倾向性评分模型下,使用简单线性相加模型得到的PS、使用非线性相加模型得到的PS与不使用PS进行遗传匹配的自变量均衡情况,可见,不使用PS作为自变量进行遗传匹配的组间自变量均衡程度更差。当计算PS的模型与真实倾向性评分模型更相近时,使用PS的遗传匹配效果更优。GM与GM+的表现大体相似,在复杂情形下GM+的表现略优于GM。从表1可见,使用PS进行遗传匹配的偏倚更小,从小到大依次为GM≈GM+ 图5 不同倾向性评分建模策略匹配各自变量均衡情况:SMD 图6 不同策略遗传匹配后各自变量均衡情况:SMD Dehejia等人创建的数据集“lalonde”基于一个全国性的职业培训研究,探讨接受职业培训是否会增加学员收入,该数据集内置于“Match”包中。该研究的研究对象共445例(试验组185例,对照组260例),基线变量包含年龄、受教育时间、人种等8个变量。结局变量为研究对象在1978年的收入。本研究使用MDM、PSM与GM对此进行分析,匹配方案与先前模拟试验中一致。匹配前后自变量均衡情况见表2及图7。匹配前,有4个自变量在两组间的SMD大于0.1(有无毕业文凭、族裔、受教育时间、年龄),其中“有无毕业文凭”在两组间的P值小于0.001。使用三种方法匹配后自变量均衡情况均有所改善,但GM匹配后两组自变量均衡性最高,匹配后两组SMD最小。 表2 匹配前后自变量特征 图7 匹配前后两组标准化差异 本文在简要介绍利用进化算法自动迭代地构建匹配度量的遗传匹配的基础上,借助Monte-Carlo模拟方法,通过效应估计的准确性及匹配后组间自变量的均衡性两个方面评价了马氏距离匹配、倾向性评分匹配和遗传匹配在数据不同复杂度下的统计性能。模拟结果显示,当指定的倾向性评分模型与真实的倾向性评分模型相近时,倾向性评分匹配表现出了较好的统计学性能。但当模型复杂度上升后,即指定的倾向性评分模型与真实模型相差较大时,倾向性评分匹配的偏倚开始增大。而遗传匹配不会受真实模型的影响,在不同模型复杂度下得出的效应估计偏差最小,匹配后两组自变量均衡性最高。实例分析结果也验证了,遗传匹配在保持较多匹配例数下仍能达到最好的组间均衡。 近年来,倾向性评分匹配在医学研究中得到了广泛的应用,但在实际使用中仍存在着如何确定合理倾向性评分模型的问题。Granger等人统计了在2014年到2016年发表在高影响因子的医学期刊上使用倾向性评分进行分析的研究,其中20.9%(187/894)的研究并未阐述如何评估所建立的倾向性评分模型的合理性[13]。通常情况下,当研究人员根据数据特征并结合自身专业知识尽可能地纳入混杂因素,确定倾向性评分模型后,可以通过评价匹配后自变量平衡情况来判断是否指定正确并进行调整。Rosenbaum和Rubin曾建议应根据匹配后自变量均衡情况迭代修改倾向性评分模型已达到最优均衡,但在实际情况中许多研究者缺乏这种建立合理的倾向性评分模型的意识或技能,这无疑会导致倾向性评分匹配在医学研究中的错用,得到并不真实的研究结论。 遗传匹配将损失函数定义为匹配后组间均衡性指标,利用遗传算法自动地找到最优的匹配组合,从而实现自变量的均衡。与倾向性评分匹配相比,遗传匹配不需要研究者严格指定倾向性评分模型,不需要研究者根据匹配后自变量平衡情况手动调整倾向性评分模型,这极大地降低了研究者的工作难度。目前尚无评价匹配后自变量均衡性的最优指标,除最常见的组间检验P值及标准化差值外,还有方差比、Hosmer-Lemeshow检验统计量、KS检验统计量及C统计量等[13]。在本文使用的R软件包“Matching”中则可自定义损失函数,使用任何均衡性指标进行遗传匹配。遗传匹配获得最优的匹配度量后,匹配的方案与其他类似。传统的最近邻匹配、卡钳匹配、1:n匹配等在遗传匹配中仍可使用。 当然,遗传匹配与其他匹配方法一样,只能处理已知的混杂因素,对未知混杂无法控制,也不适用于时依自变量所致混杂因素的处理[8-9];当其使用倾向性评分作为自变量进行匹配时,也面临倾向性评分模型自变量的选取问题。 本研究评价了使用不同倾向性评分建模策略对倾向性评分匹配和遗传匹配的影响程度,研究结果表明,在建立倾向性评分模型时,考虑自变量的非线性关系会提高匹配的效果。另外,与不纳入PS的遗传匹配相比,纳入PS进行遗传匹配具有更好的统计性能,且当使用的倾向性评分模型越正确,遗传匹配的效果越好,这恰好支持了Diamond等人的建议。这一结论也符合双重稳健估计的理论[14],即纳入PS的遗传匹配提升了效应估计的稳健程度。 在真实世界研究中,为去除混杂因素的影响,得到无偏的效应估计,众多学者提出了许多方法,例如传统的分层分析、多因素回归分析、倾向性得分匹配、逆概率加权匹配、重叠加权等方法。近年来一些更为复杂的方法也被提出,例如G估计、双重稳健估计等方法。本文因篇幅所限,仅比较了三种匹配方法的统计表现,遗传匹配与其他方法的比较有待进一步研究。 本研究只比较了在设定的模拟情形下三种匹配方法的结果,此假设下模拟数据尽管能满足组间倾向性评分的重叠假定(overlap assumption),但并未对方法的匹配度进行探讨比较,也未探讨两组倾向性评分的重叠程度对匹配效能的影响;另外,本研究的模拟试验只考虑了1∶1有放回的匹配策略,未进行其他比例的匹配,这些问题均有待进一步研究。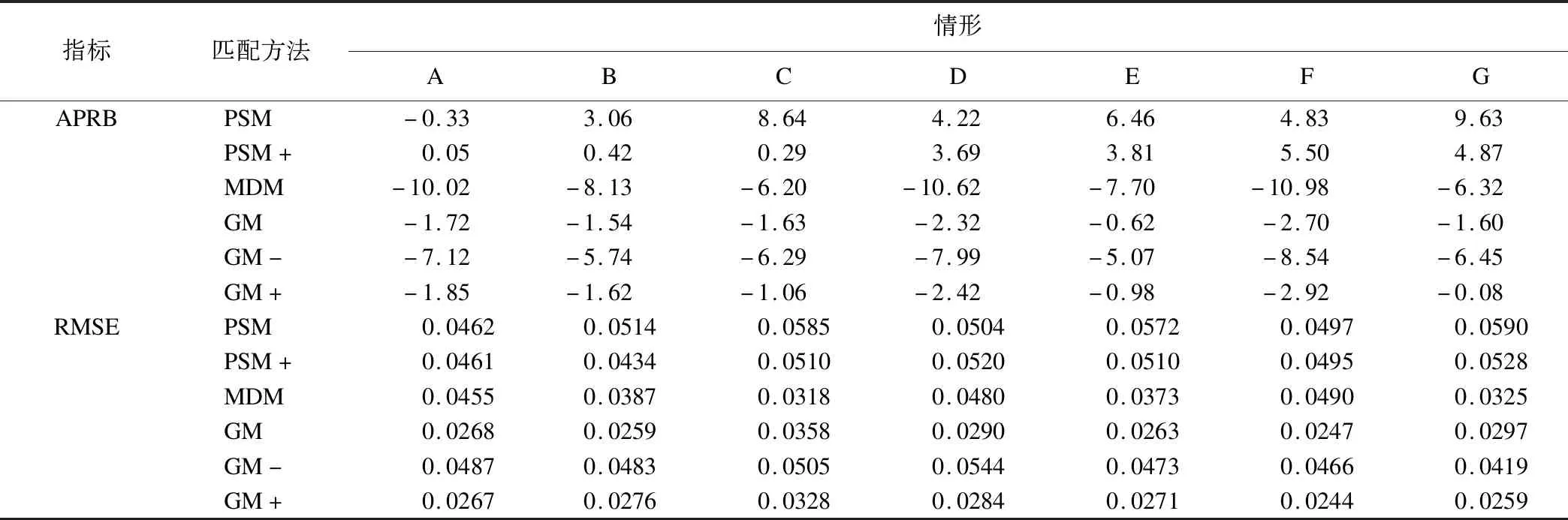


案例分析

讨 论
