电场调控双层WSe2 转角同质结激子莫尔势*

石蓓蓓 陶广益 戴宇琛 何霄 林峰 张酣 方哲宇

(北京大学物理学院,人工微结构和介观物理国家重点实验室,北京 100871)

二维过渡金属硫化物构成的范德瓦耳斯异质结由于存在晶格失配或层间相对旋转角度会产生周期性的莫尔条纹结构,由此引入的纳米尺度莫尔周期势可以影响激子的空间传输过程.目前有关双层过渡金属硫化物转角同质结中激子莫尔势调控的研究比较有限,本工作利用第一性原理计算研究了外加垂直电场对不同旋转角度的双层WSe2 同质结激子莫尔势的影响,发现层间激子莫尔势的大小和势垒/势阱的位置与层间相对旋转角度及电场强度有关,不同旋转角度的双层WSe2 同质结激子莫尔势大小及势垒/势阱的位置随电场强度(≤ 1 V/nm)的变化不同.这些结果为调控层间激子的局域与非局域转变提供了理论依据和数据预测,在推动人工激子晶体及纳米阵列激光器等半导体器件的发展方面具有重要指导意义.

1 引言

自2004 年以来,二维材料一直是物理学界中研究内容最多的材料体系,并在纳米光电、半导体器件等领域得到了广泛应用.近年来,由石墨烯、六方氮化硼(h-BN)和过渡金属硫属化物(transition metal dichalcogenides,TMDCs)等二维材料,通过层间相互作用构成的范德瓦耳斯异质/同质结以层内共价键和层间范德瓦耳斯力为特征形成了一个新兴的研究领域,可以让人们深入研究二维材料中一些不寻常特性和新现象[1].

当组成范德瓦耳斯异质/同质结构的两种材料存在晶格失配或层间相对旋转角度时,会在平面内产生比每层拥有更长周期性的莫尔条纹并形成莫尔超晶格,同时在层间引入纳米尺度的周期性势场,从而成为研究量子反常霍尔效应及强关联量子态等物理现象的良好平台[2,3].在石墨烯/h-BN 组成的范德瓦耳斯异质结中,该周期势可以调控石墨烯本征狄拉克点处的电子特性,诱导出次级狄拉克点,从而打开本征石墨烯带隙.在低温强磁场环境下,还能够在该体系中观察到霍夫施塔德蝴蝶图案(Hofstadter butterfly pattern)[4-6].最近几年的研究表明,由两个单层石墨烯以大约1.1°的角度堆叠形成的“魔角”石墨烯同样具有丰富的物理性质,通过施加垂直电场来调控其载流子浓度,可以让石墨烯实现由绝缘体到超导体的转变[7,8].

TMDCs 由于空间反演对称性破缺而天然具有半导体能隙,是低维纳米材料领域的热门研究对象.本征二维TMDCs 材料中存在强自旋-轨道耦合作用,由此引起的能谷与自旋序数锁定使其在谷效应调控及低维谷电子学器件等领域具有重要研究意义[9].由于单层TMDCs 的带隙各不相同,因此由单层TMDCs 材料堆叠形成的同质/异质结具有更加丰富的能带结构和光学性质.TMDCs 范德瓦耳斯异质结具有II 型能带对齐,导带和价带的极值点位于不同的材料层,由不同层极值点处的电子和空穴组成的电子-空穴对叫作层间激子,其拥有比层内激子更长的寿命,在实现远程激子和谷自旋传输方面具有极大的潜在应用[10].在TMDCs同质/异质结中,由材料晶格失配或层间相对转角引入的外加周期势场为激子莫尔势[11],可以调控TMDCs 转角体系中层间激子的物理性质.基于密度泛函理论(density functional theory,DFT)的第一性原理计算预测了莫尔势可以将层间自由激子局域化,使得原来的层间激子峰附近出现新的激子态—莫尔激子.进一步地,已经有研究通过远场光学测量证实了TMDCs 转角异质结中莫尔激子的存在[12-15].这些研究使得TMDCs 转角材料在制造高性能半导体激光器、单光子发射器阵列以及纠缠光子源等方面具有潜在应用[16,17].

目前已有的工作对于TMDCs 转角同质结中激子莫尔势的研究比较有限,并且在调制莫尔势大小从而能够操纵激子的局域与非局域转变方面的研究几乎空白.因此,本研究利用第一性原理计算的方法研究外加垂直电场对转角分别接近0°和60°的双层WSe2同质结层间激子莫尔势的主动调控.结果表明,在转角接近0°的双层WSe2中,当施加的电场强度小于1 V/nm 时,激子莫尔势的大小会随电场强度的增大发生改变;而在转角接近60°的体系中,其莫尔势的大小及势垒/势阱的位置都会随电场强度的变化而改变.本工作的研究结果为实验上利用外加电场操纵激子的局域与非局域转变,进而实现其空间扩散行为的主动调控提供了数据预测,为未来设计和制备人工激子晶体及局域纳米阵列激光器等半导体器件提供了理论依据.

2 理论模型和计算方法

2.1 理论模型

本研究采用从头计算连续模型(ab initiocontinuum model)方法来计算双层WSe2转角同质结激子莫尔势随实空间位置的变化关系[18,19].图1(a)是转角为θ具有AA堆叠次序的双层WSe2(AAWSe2)示意图,其中d为面内晶格间相对位移.以底层W 原子为坐标原点建立直角坐标系,则双层WSe2的原始晶格平移矢量为

图1 (a) 转角θ 接 近0°晶胞AA-WSe2 的 图示;(b) 单层WSe2 第一布里渊区(绿色六边形)及其倒格矢 G j ;(c) WSe2晶格的 对称操作,黑色箭头表示由 导致的相位变化;(d) 双层WSe2 转角同质结莫尔单胞的布里渊区及相应的倒格矢bjFig.1.(a) Illustration of AA-WSe2 homobilayer with a small twist angle θ;(b) first-shell reciprocal lattice vectors Gj of a monolayer WSe2 triangular lattice and the corresponding Brillouin zone (green hexagon);(c) transformation of the WSe2 lattice (Black arrows denote the phase change by );(d) moiré reciprocal lattice vectors bj and corresponding Brillouin zone.

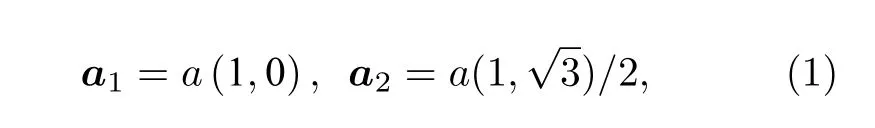
其中a为单层WSe2的晶格常数.

双层WSe2转角同质结层间激子势能的大小Eg-Eb与超晶格实空间的位置有关,其中Eg为动量空间K点对应的导带底和价带顶之间的能隙,Eb为激子的束缚能.由于莫尔条纹结构的存在使得Eb的变化量小于Eg的变化量,因此在整个计算过程中可以忽略Eb的变化.由于能隙的变化Δ0是关于晶格间相对位移d的周期函数,因此可以通过最低谐波展开来充分近似[20-23]:

又因Δ0为实数,所以有V1=,且V1=Vexp(iψ),其中ψ表示莫尔势形状的参数,决定莫尔势能量极值点(势垒/势阱)的位置.

将倒格矢Gj代入(2)式中,化简得:

在小转角的双层异质/同质结材料体系中,由于位移d在莫尔周期内的变化比较缓慢,因此可以假设能隙的变化局部跟随位移的变化,所以有

将莫尔单胞倒格矢bj及实空间的全局位移表达式代入(5)式中并化简,可以得到超晶格中激子莫尔势随实空间位置变化的关系式:

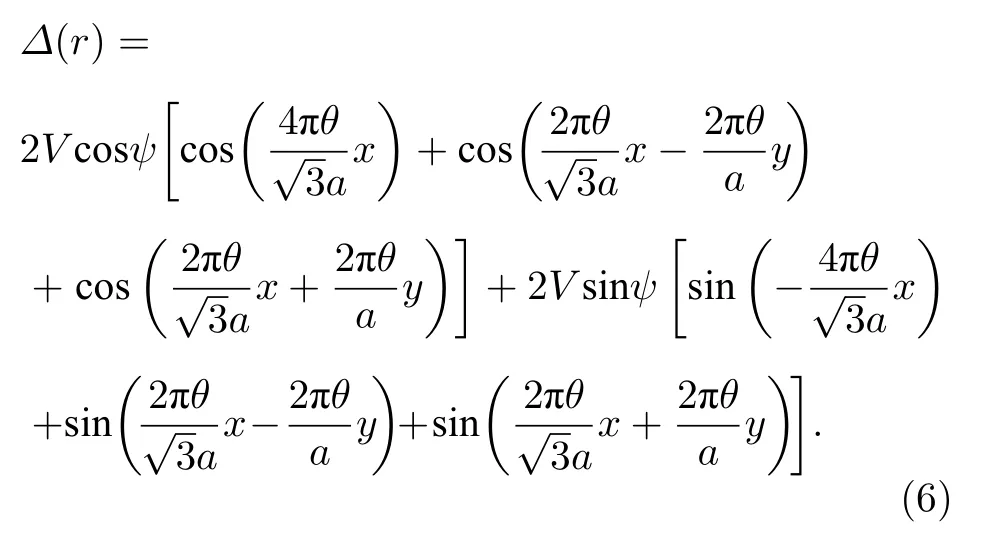
2.2 计算方法

本研究利用Materials Studio 构造AA堆叠和3R堆叠的双层WSe2原胞模型.考虑到后续的计算过程要施加电场,因此在垂直于平面方向设置的真空层厚度大于20 Å (1 Å=10—10m),避免相邻层间原子的影响.使用基于DFT 的VASP 软件包[24]进行模型结构优化、电荷密度自洽以及能带结构的计算,过程中采用投影缀加平面波方法(projectoraugmented wave,PAW)[25],使用PBE 形式的广义梯度近似(general gradient approximate,GGA)计算交换关联函数,并加入范德瓦耳斯修正(采用DFT-D2 方法)[26],平面波截断能设置为400 eV.在结构优化过程中,固定单层WSe2平面 (x-y平面) 内各个原子的位置,采用高斯变换仅在真空层方向(z方向)对原子位置进行弛豫.每个原子的能量收敛标准设置为1 × 10—7eV,晶体内应力收敛标准为低于1 × 10—3eV/Å,采用Monkhorst-Pack方法选择11 × 11 × 1 的k点.此外,电荷密度自洽和能带计算过程中都考虑了自旋-轨道耦合效应.

3 结果和讨论

3.1 双层WSe2 转角同质结

在构建双层WSe2时引入层间相对旋转角度θ会产生周期性莫尔条纹并形成莫尔超晶格,如图2(a)所示,绿色菱形线框表示莫尔超晶格.莫尔周期aM=a/θ.

在具有较小转角的双层WSe2中,其莫尔超晶格顶点附近以及沿长对角线方向上两个特殊位置处的晶格构型具有高度对称性,如图2(a),(b)中的红色、黑色及蓝色圆形虚线所示.对于转角接近0°的双层WSe2而言,其莫尔超晶格中几个特殊位置处的晶格结构可以近似视为具有AA堆叠次序(AA-WSe2)或3R堆叠次序(3R-WSe2)的双层WSe2的晶格结构.图2(b)显示的是AA-WSe2的俯视图(上)及侧视图(下),可以看到AA-WSe2的结构特征是上层Mo 原子位于下层Mo 原子正上方,上层S 原子位于下层S 原子正上方.图2(c)为3R-WSe2的俯视图和侧视图,其结构特征是上层Mo 原子位于下层S 原子正上方,与上层Mo 原子相连的S 原子则恰好位于下层六角晶格的中心位置处.从图2(b),(c)可以看出,AA-WSe2的上层或下层沿着晶胞中长对角线的方向平移一定的距离可以得到3R-WSe2,反之亦然.

对于转角接近60°的双层WSe2而言,其莫尔超晶格顶点以及长对角线方向上两个特殊位置处的晶格结构,可以近似视为具有2H堆叠次序(2HWSe2)或AB′堆叠次序(AB′-WSe2)或A′B堆叠次序(A′B-WSe2)的双层WSe2的晶格结构,如图2(d)所示.图2(e)为2H-WSe2的俯视图和侧视图,其结构特征是上层Mo 原子位于下层S 原子正上方,上层S 原子位于下层Mo 原子正上方.图2(f)是AB′-WSe2的俯视图和侧视图,其结构特征是上层Mo 原子位于下层Mo 原子正上方,所有的S 原子都位于六角晶格的中心位置处.图2(g)是A′B-WSe2的俯视图和侧视图,其结构特征是上层S 原子位于下层S 原子正上方,而所有的Mo 原子都位于六角晶格的中心位置处.可以看出,2H-WSe2、AB′-WSe2和A′B-WSe2同样可以通过上下层之间的相对平移而相互得到.此外,从图2(b),(g)和图2(c),(e)中可以得知AA-WSe2通过旋转能够得到A′B-WSe2,3R-WSe2通过旋转则可以得到2H-WSe2.

图2 (a) 转角接近0°的莫尔条纹及莫尔超晶格;(b),(c) 分别为AA-WSe2 和3R-WSe2 晶格结构的俯视图(上)和侧视图(下);(d) 转角接近60°的莫尔条纹及莫尔超晶格;(e)—(g) 分别为2H-WSe2,AB′-WSe2 和A′B-WSe2 晶格结构的俯视图和侧视图Fig.2.(a) Schematic of the long-period moiré superlattice formed in real space at 0°;(b),(c) top (top) and side (bottom) views of two high-symmetry stacking patterns of AA-WSe2 and 3R-WSe2;(d) schematic of the long-period moiré superlattice formed in real space at 60°;(e)—(g) top and side views of two high-symmetry stacking patterns at 60° of 2H-WSe2,AB′-WSe2 and A′B-WSe2.

对于具有不同旋转角度的双层WSe2体系而言,其莫尔超晶格高对称点位置对应的晶格构型只有AA-WSe2,3R-WSe2,2H-WSe2,AB′-WSe2和A′B-WSe2这5 种,其中前两者晶格构型对应转角为0°的双层WSe2,后三者对应转角为60°的双层WSe2.因此,本文选择转角为0°和60°的双层WSe2同质结进行研究.

3.2 能带结构和激子莫尔势

研究计算了AA-WSe2,3R-WSe2,2H-WSe2,AB′-WSe2以及A′B-WSe2在不同电场强度下的能带结构.根据从头计算连续模型方法,将DFT 计算所得的不同电场强度下、不同堆叠次序的双层WSe2的能隙Eg,分别对应地近似看作不同转角体系下莫尔超晶格中5 个特殊位置处具有高对称性晶格构型的能隙Eg(d),然后将Eg(d) 代入(4)式中并利用Mathematica 进行数据拟合,得到转角分别接近0°和60°的双层WSe2同质结中层间激子莫尔势在不同电场强度下的大小及形状参数V和Ψ,最后将莫尔势参数V和Ψ代入(6)式,就可以得到不同转角体系莫尔超晶格中激子莫尔势随实空间位置及电场强度的变化关系.

图3(a)是电场分别为0,1 V/nm 时2H-WSe2的能带结构图,其中红色实线为不加电场时2HWSe2的能带结构,可以看到其动量空间K点对应的导带底和价带顶之间的能隙Eg约为1.38 eV,由此可知2H-WSe2中K-K层间激子的能量约为1.38 eV;黑色虚线是场强为1 V/nm 时2H-WSe2的能带结构.从图3(a)可以看出,在外加电场的影响下2H-WSe2的导带能量降低,导致K-K层间带隙减小.图3(b)为图3(a)中K点价带的放大图像,可以看到K点对应的价带同样随着电场强度增大而发生移动.此外还发现,不同场强下K点对应的导带底和Q点(K和Γ的中点)对应的价带顶之间的能隙总是最低,因此可以推测出K-Q层间激子代表跃迁基态,图3(c)为本征2H-WSe2在动量空间Q点处导带底(conduction band minimum,CBM)和K点处价带顶(valence band maximum,VBM)的二维电荷密度图,等值面的取值为0.002 eV/Å3.

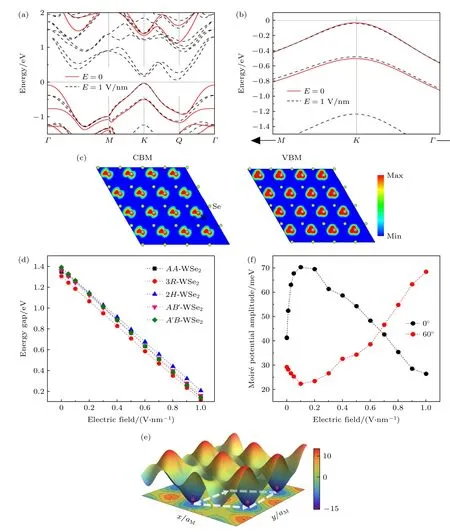
图3 (a) 电场强度为0,1 V/nm 时2H-WSe2 的 能带 结构图;(b) 2H-WSe2 在K 点处 对应价带的 放大 图;(c) 2H-WSe2 在Q 点处CBM 及K 点处VBM 的W 原子的二维电荷密度图;(d) 不同电场强度下5 种堆叠次序的双层WSe2 在K 点对应的能隙;(e) K-K激子莫尔势随实空间位置变化的三维及二维投影示意图,可以将激子(红色和黑色小球)束缚在莫尔势最低位置处;(f) 转角接近0°/60°的双层WSe2 中K-K 激子莫尔势大小随电场强度的变化Fig.3.(a) Band structure diagram of 2H-WSe2 when the electric field is 0,1 V/nm;(b) enlarged view of the valence band maximum at K-point of 2H-WSe2;(c) 2D plots of partial charge density CBM and VBM states of 2H-WSe2 at Q-point and K-point of W atom,respectively;(d) band gap corresponding to K-point in momentum space of double-layer WSe2 with five stacking orders under different electric filed intensity;(e) illustrations of the K-K moiré potentials in both 3D and 2D projections that can trap interlayer excitons (red and black spheres) in the local minima;(f) electric field intensity-dependent of K-K moiré potentials in twisted WSe2 homobilayers with rotation angle close to 0°/60°.

当所加的电场强度超过1 V/nm 时,DFT 计算结果显示不同堆叠次序的双层WSe2的能带结构会发生严重变形,因此本研究只给出了电场强度小于1 V/nm 时不同电场强度下5 种堆叠次序的双层WSe2的能隙,如图3(d)所示.可以看到,不同堆叠次序的双层WSe2中动量空间K点对应的层间带隙Eg均随着电场强度的增大而减小.其中,AA-WSe2和3R-WSe2的能隙差随着场强增大而减小,2H-WSe2和AB′-WSe2的能隙差随着场强增大而增大.在此需要特别说明的是,实验中所施加的电场强度可以超过1 V/nm 而不发生击穿现象,因此,实验中可以调控的电场强度范围更大.

将不加电场时2H-WSe2,AB′-WSe2和A′BWSe2的K-K能隙代入(4)式中,利用Mathematica 进行数据拟合得到参数(V,Ψ)=(2.8 MeV,83.2°).将参数V和Ψ代入(6)式,就可以得到电场强度为0 的情况下,转角接近60°的双层WSe2中K-K激子莫尔势随实空间位置的变化.正如图3(e)所示的K-K激子莫尔势随实空间位置变化的三维及二维投影图,白色菱形虚线框表示莫尔超晶格,x,y坐标轴的单位为莫尔周期aM.从图3(e)中可以看到莫尔势势垒的能量约为15 MeV,势阱的能量为—15 MeV,因此K-K激子莫尔势的大小(势垒与势阱的能量差值)约为30 MeV.由于材料中的激子从一个位置移动到另一个位置时会遇到这些能量势垒或势阱,从而影响原有激子的空间扩散行为[27-30].在实验上可以利用电子倍增相机采集激光光斑图像及泵浦激子历经超快俄歇过程后的均匀扩散发光图像,得到激子有效扩散系数的变化.结合激子的空间动力学理论及激子的泵浦超快过程,进一步分析可以得到其空间扩散行为的变化.

本研究还计算了不同电场强度下转角接近0°/60°的双层WSe2中K-K激子莫尔势的大小,得到其随电场强度的变化.结果如图3(f)所示,随着电场强度增大,转角接近0°的双层WSe2中激子莫尔势逐渐增大;当电场强度为0.1 V/nm 时,莫尔势达到最大值70 MeV;随着电场强度继续升高,莫尔势逐渐减小.对于转角接近60°的双层WSe2而言,其莫尔势大小随电场强度变化的关系正好相反,随着电场强度增大,激子莫尔势逐渐减小;当电场强度为0.1 V/nm 时,莫尔势达到最小值,约为20 MeV;随着电场强度继续升高,莫尔势逐渐增大.DFT 计算结果表明了双层WSe2转角同质结中的激子莫尔势也与材料的旋转角度有关,不同转角体系的莫尔势大小随电场强度变化的关系不同.

将不同电场强度下的莫尔势参数V和Ψ代入(6)式中,可以得到不同转角体系下莫尔势大小及能量极值点的位置随电场强度的变化关系,如图4 所示.DFT 计算结果表明在不同电场强度下,转角接近0°的双层WSe2中的K-K激子莫尔势只有大小发生改变,而势垒/势阱位置不变.电场强度为0,0.5,1.0 V/nm 时该转角体系中K-K激子莫尔势的二维投影图如图4(a)—(c)所示,白色菱形线框表示莫尔超晶格.从图中可知,莫尔势随着场强增加先增大后减小,但是势垒和势阱始终分别位于具有AA和3R堆叠次序的高对称位置处.在转角接近60°的双层WSe2中,K-K激子莫尔势的大小和势垒/势阱位置都会随着场强变化而改变,如图4(d)—(f)所示: 场强为0 时,K-K莫尔势势垒和势阱分别位于A′B和AB′位置处;场强为0.5 V/nm 时,2H位置为势垒,AB′位置为势阱;场强为1 V/nm 时,莫尔势增大,2H位置仍为势垒,势阱位置则又变到A′B处.

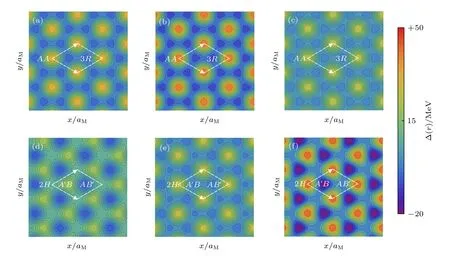
图4 电场强度不同时,转角接近(a)—(c) 0°和(d)—(f) 60°的双层WSe2 中K-K 激子莫尔势随实空间位置变化的二维投影图(a),(d) 0 V/nm;(b),(e) 0.5 V/nm;(c),(f) 1.0 V/nmFig.4.Illustrations of 2D projections of K-K moiré potentials in WSe2 homobilayers with rotation angle close to (a)—(c) 0° and(d)—(f) 60° with different electric field intensity: (a),(d) 0 V/nm,(b),(e) 0.5 V/nm;(c),(f) 1.0 V/nm.

DFT 计算结果表明,外加垂直电场可以调控双层WSe2转角同质结中激子莫尔势的大小和能量极值点的位置,因此,理论上可以通过外加电场来实现层间激子空间传输行为的主动调控.本研究的计算结果为实验上研究TMDCs 转角体系中层间激子的空间扩散过程提供了理论支持及数据预测,即在实验上可以通过施加外场来调控双层WSe2转角同质结中的激子莫尔势,使得沿材料体系实空间中某一方向的莫尔势增大,则原来沿该方向扩散的自由激子会发生局域化,从而阻碍激子空间扩散行为.反之,通过调控外加电场的大小,还可以减小沿体系实空间中某一方向的莫尔势,使得该方向上某些位置的局域激子脱离束缚态成为自由激子,从而实现激子的局域与非局域转变.因此,通过调控TMDCs 转角体系中层间激子莫尔势的大小和能量极值点的位置,可以实现纳米尺度的激子局域点阵列,这对未来设计激子晶体及纳米阵列激光器具有指导意义.

4 结论

本工作利用第一性原理计算研究了外加垂直电场对双层WSe2转角同质结K-K激子莫尔势大小和势垒/势阱位置的主动调控,揭示了不同旋转角度下双层WSe2同质结中层间激子莫尔势随电场强度及实空间位置的变化关系.DFT 计算结果表明,不同转角体系的激子莫尔势随电场强度的变化不同,转角接近0°的双层WSe2同质结激子莫尔势随着电场强度的增加先增大后减小,当电场强度为0.1 V/nm 时,激子莫尔势有其最大值(70 MeV);对于转角接近60°的体系而言,其激子莫尔势随着电场强度的增加先减小后增大,当电场强度为0.1 V/nm 时,激子莫尔势达到最小值(20 MeV).莫尔势可以影响激子的空间扩散行为,本研究为实验上利用外加电场操纵激子的局域与非局域转变,从而实现其空间扩散行为的主动调控提供了理论依据和数据预测,在未来推动人工激子晶体乃至纳米阵列激光器等半导体器件的构造方面具有重要的指导意义.

感谢北京大学高性能计算校级公共平台的支持.