基于人工智能控制策略的微电网自动调度优化方案

陈亚琼 马潇予 曾小凤 张克诚 管鑫

（1.国网甘肃省电力公司培训中心 2.国网甘肃省电力公司酒泉肃州区供电公司3.国网甘肃省电力公司临夏供电公司）

0 引言

随着全球能源危机的日益加剧以及环境问题的持续恶化，世界各国都在对风能、太阳能等新型能源进行研究，加大新能源的利用占比，逐步取代原有的化石型能源，新能源的应用必须先以分布式电源、储能装置的形式接入微电网，通过微电网进行控制后才能够接入主电网，因此对微电网的运行模式进行合理的调度优化是保证新能源高效利用的关键。

本文所研究的微电网自动调度优化问题实质上是基于多约束条件的单目标优化问题。微电网能够进行调度优化的前提是电网能够接入主电网运行，通过微电网内部的调度优化以及与主电网的配合运行，向负荷提供高质量的能源。本文针对包含有多种分布式电源、储能装置、可控负荷的微电网，以微电网的运行成本为优化目标，构建微电网调度模型，采用人工智能控制策略进行模型的求解。通过仿真实例进行深入分析，人工智能控制策略能够实现微电网的自动化调度。

1 微电网架构

电网的负荷重要性存在一定的差异，通常情况下可以划分为三种，即核心负荷、重要负荷、常规负荷，三种类型的负荷分别配置在三条配电网馈线上，以便实现对负荷的分级控制，微电网通过公共结点接入到主电网中，并网运行，微电网的具体调度架构如图1所示。

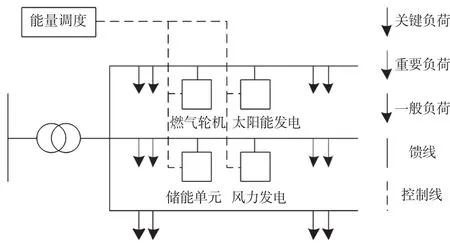
图1 微电网调度架构

微电网的分布式电源又可以分为新能源发电单元（包括风力发电单元、光伏发电单元）和常规发电单元（火力发电单元），分布式电源所发出的电能除向主电网输送外，还可以输送到储能装置进行存储，当达到特定的外部条件时，储能装置会向外输出电能，为微电网中的负荷供电。

2 分布式电源数学模型

该微电网包含多种形式的分布式电源，如光伏发电、风力发电、火力发电等，还包括储能装置和负荷。

2.1 光伏发电数学模型

光伏发电的输出功率与光照强度、功率点极大值的跟踪控制、光伏阵列的受光面积、光伏电池的工作效率、光线的入射角度相关联，其输出功率的数学表达式：

式中，v为光照强度；λpV为最大功率点跟踪控制效率；UpV为光伏阵列面积；ρpV为光伏电池工作效率；θ为太阳光入射角度。

2.2 风力发电数学模型

风力发电的输出功率由当前风速和风力发电机的额定功率相关联，风力发电的输出功率为：

式中，vin为风力发电机并网发电风速下限；vout为风力发电机并网发电风速上限；vR为风力发电机的额定风速；PR为风发电机的额定输出功率。

2.3 火力发电数学模型

火力发电成本可以通过如下公式进行数学描述：

式中，CCoal为燃料出售价格；ωCoal为燃料的热净值；PFire(t)为火力发电机组当前实时输出功率；PFire(t)为火力发电机组当前实时工作效率。

2.4 储能装置数学模型

当储能装置工作在充电状态时，其功率方向向内，即输出功率为负，当前时刻的存储能量为：

当储能装置工作在放电状态时，其功率方向向外，即输出功率为正，当前时刻的存储能量为：

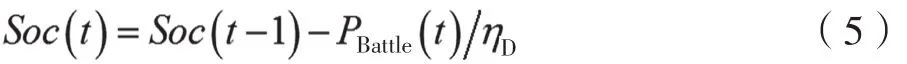
式中，Soc(t)和Soc(t-1)为当前时刻和前一时刻的储能装置存储的能量；PBattle(t)为储能装置的实时输出功率；ηC和ηD为储能装置的充电和放电效率。

3 微电网调度模型

3.1 调度目标函数

保证微电网运行效益的最大化就是通过对微电网的运行状态进行调度，调节微电网中各个分布式电源和储能装置的运行状态，实现微电网运行成本最低。则微电网的调度目标函数可以描述为：

式中，CCoal(t)为火力发电的燃料成本；CDep(t)为电力设备的折旧成本；CKeep(t)为电力设备运营保养成本；CCut(t)为负荷切除补偿成本。

3.2 自动化调度约束条件

（1）系统功率约束条件

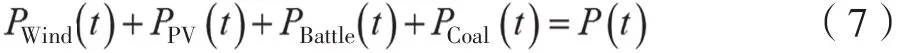
式中，PWind(t)为风力发电单元的输出功率；PPV(t)为光伏发电单元的输出功率；PBattle(t)为储能装置的输出功率；PCoal(t)为火力发电单元的输出功率；P(t)为微电网的负荷需求。

（2）分布式电源功率约束条件

式中，Pi,min为所有的分布式电源输出功率的最小值；Pi,max为所有的分布式电源输出功率的最大值。

（3）功率传输约束条件

式中，Pgrid,min为功率传输的最小值；Pgrid,max为功率传输的最大值。

（4）储能装置运行约束条件

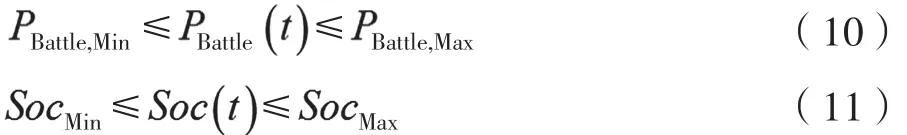
式中，PBattle,Min为储能装置充电功率的最小值；PBattle,Max为储能装置充电功率的最大值；SocMin为储能装置允许容量的最小值；SocMax为储能装置允许功率的最大值。

4 人工智能控制策略

4.1 控制策略基本原理

在微电网自动调度上采用蜂群策略，该策略是基于蜂群的搜索行为而产生的一种人工智能算法，在全局最优解和局部最优解求解方面性能优异，尤其适用于本文这种单目标优化问题，基于多约束条件对单目标最优解进行求解。单目标优化问题会涉及一个收敛性指标，并且要求蜂群搜索到的最优解位于样本空间中，由此便解决单目标优化问题，将蜂群策略应用到单目标的微电网自动化调度控制。

4.2 基本蜂群算子

（1）起始时段

在这个时段，需要对蜂群样本的具体参数进行初始化设置，具体有样本空间维度、样本集合数量、控制参数、迭代参数、食物源数量参数等，然后基于设定好的参数对蜂群样本集合进行初始化：

假定食物源Nj=(nj1,nj2, … ,njM)为蜂群样本集合中第j个食物源的当前所处位置，M为蜂群样本集合的空间维度，在这个空间中，每个食物源的起始位置描述如下：

式中，m=1, 2, …,M；Qm和Xm分别是整个蜂群样本集合空间中第m个维度的集合空间边界；Randi.m是区间[0,1]上的均匀分布随机数。

（2）雇佣蜂时期

雇佣蜂在进行搜索时，一旦搜索到食物源后对食物源的具体参数进行存储，并将数据传输给辅助蜂。对于蜂群样本空间中的任意一个食物源，雇佣蜂是随机选择路径进行食物源搜索的，搜索到的食物源位置为：

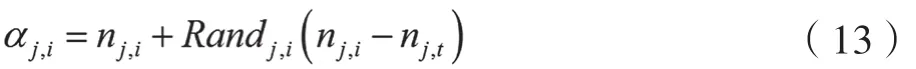
式中，j为雇佣蜂；i为雇佣蜂所处的当前维度；t为其他随机选取的雇佣蜂；Randi.i是区间[0,1]上的均匀分布随机数。再对雇佣蜂的匹配度参数进行综合评价，以确定哪个匹配度更好，并确定为当前认定的雇佣蜂。

（3）辅助蜂阶段

辅助蜂会分析从雇佣蜂传输来的食物源具体参数，以确定从哪个方向开采食物源，在这个时段辅助蜂会根据自己的匹配度参数运算出对应的进化概率，以选取最优辅助蜂个体进行深度寻优。蜂群样本空间中的第j个样本个体的进化概率，可以由如下数学公式进行描述：

式中，S为蜂群样本空间中的样本的个数；mat(ni)为匹配度函数，进化概率越大意味着辅助蜂的在高质量食物源附近进行食物搜索的概率就越高。

（4）搜寻蜂时段

当雇佣蜂和辅助蜂附近食物源被完全搜索完毕或在规定搜索次数内无法搜索到新的食物源时，雇佣蜂会变身为搜寻蜂，根据式（12）的位置描述，进行位置变换，继续展开搜索，直至达到搜索结束条件，再进行下一步动作。

5 实例分析

以某地微电网为例进行分析，该微电网架构与图1中所描述的微电网架构完全一致，对本文提出的人工智能控制策略进行验证，该微电网的容量上限为100kVA，微电网的电压等级为400V。在满足微电网的多重调度约束条件下，分布式电源中的光伏发电和风力发电均工作在最大功率跟踪模式下，因此火力发电以及储能装置是进行优化主要控制对象。当光伏发电和风力发电总的输出功率超过负荷所需功率时，火力发电的输出功率应当保持在最低水平，储能装置从外部吸收电能，工作在充电状态；当光伏发电、风力发电、火力发电，储能装置的输出功率均达到极限时，所能提供的能量无法满足系统所需负荷，应当根据负荷重要性为依据，适当切除重要性等级较低的负荷。

以发电运行成本最低目标进行运算，最终得到一天24h调度方案如图2所示。

图2 微电网自动化调度方案

由调度方案中数据可知，在12～13时的时间段之内光伏发电和风力发电的总输出功率超过系统负荷所需功率，基于火力发电停机会造成成本损耗的原则，所以此时火力发电保持最低功率输出运行，多余电能传输到储能装置进行能量存储，在18～19时的时间段内，微电网中的光伏发电、风力发电、火力发电处于满负荷运行状态，微电网所能够输出的总功率无法满足负荷的需求，适当切除部分重要性等级较低负荷，保证重要性等级较高负荷的工作。

6 结束语

本文研究微电网并网模式下的自动化调度方案，基于多种外部和自身约束条件下，以发电运行成本最低为优化目标，搭建微电网自动化调度模型，采用人工智能策略进行模型的最优解寻取，仿真结果表明，本文所提出的人工智能策略的收敛性更好、收敛速度更快，很好地实现了微电网调度的发电成本最低目标，解决了微电网在并网运行模式下的自动化优化调度问题。