基于CNN与LSTM的农村电力负荷预测研究
2022-09-14杨迪张璐杨力人方亮刘继江
杨迪 张璐 杨力人 方亮 刘继江
(1.中国三峡新能源集团有限公司甘肃分公司 2.西北工业大学)
0 引言
节能型农村的建设已是我国经济发展与绿色能源可持续发展的长远目标。在“碳达峰、碳中和”与构建新型电力系统愿景下,电力系统的发展进程将迎来巨大挑战,因此,对电力负荷精准预测有利于提高电力系统的经济性、平衡性、可靠性。
国内外学者均对负荷预测进行相应的研究,王晓辉[1]等人利用PSO算法能够寻找全局最优解的特点进行LSTM超参数寻优,并与传统LSTM神经网络预测模型及BP神经网络预测模型进行对比,验证了该方法的预测精度较高。邓智广[2]针对现阶段电力负荷预测要求逐渐提高,提出一种基于贝叶斯分类的短期负荷预测模型,结果表明该预测方法较传统方法预测的精度更高。朱经红[3]基于混沌时间序列提出一种新的城网饱和负荷预测方法。结果表明,该方法预测结果较为准确,可在短时间内达到较高预测精度。
本文基于实际农村负荷数据,研究基于CNN与LSTM的电力负荷预测模型,并与ARIMA的负荷预测方法进行对比,验证了本文提出的电力负荷预测模型的优越性。
1 研究理论
1.1 预测模型
(1)CNN
卷积神经网络(CNN,Convolutional Neural Networks)是常用来处理已知网络拓扑结构的神经网络结构。随着CNN不断改进,出现许多卷积网络结构变体,包含输入层、卷积层、池化层、全连接层及输出层,卷积层用于提取底层特征,池化层实现数据维度下降并防止过拟合,全连接层汇总卷积层与池化层得到信息并输出。
(2)LSTM
长短时记忆神经网络(LSTM,Long Shortterm Memory)是一种特殊的递归神经网络(RNN,Recurrent neural network),可以解决长序列训练过程中的梯度消失和梯度爆炸问题,LSTM在长序列中有更好的表现。结构图如图1所示。
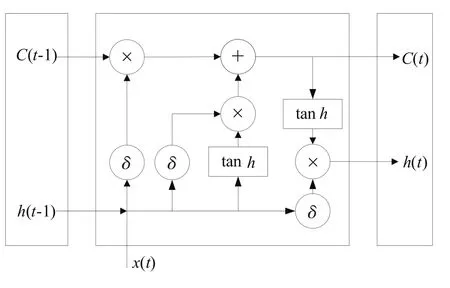
图1 LSTM结构
LSTM在训练过程中,将历史有用的信息保留,无用的信息遗忘,比RNN处理长序列问题的效果更好。常用Sigmoid激活函数输出区间为(0,1),有助于及时更新数据,Tanh与Sigmoid函数类似,但其输出区间为(-1,1)。
1.2 灰色关联分析
为提高预测精度及训练速度,需采用相关分析法筛选影响因素。灰色关联度法是灰色理论的重要分支,可分析多因素之间的关联度。因其对样本数量要求不高、计算量小等特点,本文选择该方法筛选影响因素,步骤如下。
(1)确定参考序列X0及比较序列Xi
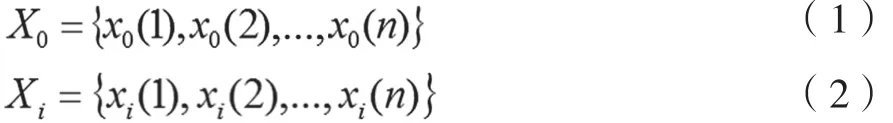
(2)采用均值化法无量纲处理

(3)计算绝对差值

(4)由绝对差值计算极差

(5)求关联度系数

(6)求灰色关联度

(7)灰色关联度排序
2 研究过程
2.1 数据处理
本文以陕西某农村地区实际负荷为研究对象,经过前期数据整理共得到数据间隔为1h的14982组数据,由于临时检修,有6天的数据存在异常,为提高预测精度,将这6天的数据经过经验修正法处理得到有效的14976组数据。
2.2 负荷特性分析
(1)季节特性
负荷变化具有一定规律,为进一步分析该地区负荷变化情况,将数据进行四季划分,得到春、夏、秋、冬负荷数据分别为184天、184天、106天、150天,具体变化如图2所示。
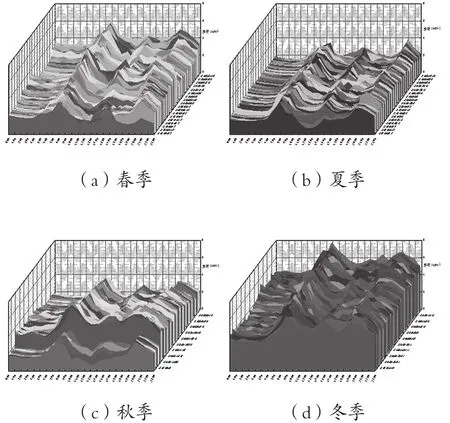
图2 四季负荷变化
由图可知,在不同季节的负荷变化趋势相似,但量级存在差异,冬季因供暖需求大,故负荷需求量较大,春季次之,夏、秋季负荷需求量较小。
(2)周负荷
周负荷变化如图3所示。
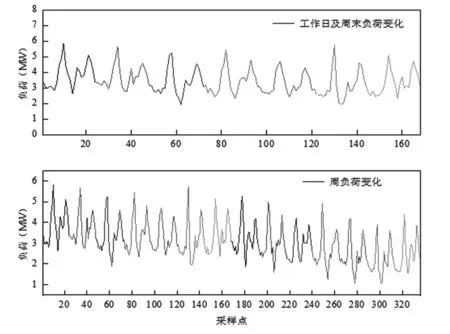
图3 周负荷变化曲线
由图3可知,周负荷曲线变化具有周期性。农村用户负荷变化情况不同于学校或其他办公场所,工作日与休息日并无较大差异。
(3)日负荷
本文以春分、夏至、秋分及冬至四个典型日为例,分析日负荷的变化情况。
由图4可知,日负荷变化趋势呈“三峰两谷”特性,冬至因供暖需求使得负荷值较大,波峰出现早上7~9时、下午13~15时、晚上19~21时,反映了农村用户日常生活。
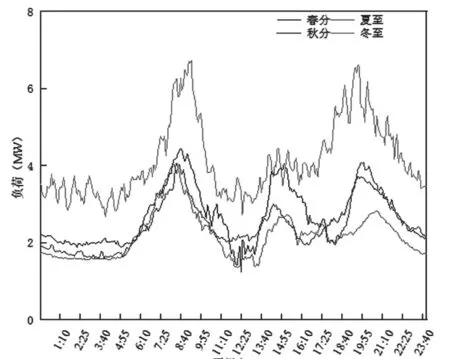
图4 日负荷变化特性
2.3 气象因素
结合1.2节内容,本文选择温度、露点、湿度等参数作为灰色关联度比较序列,实际负荷值为参考序列,各参数与负荷的关联度如表1所示。
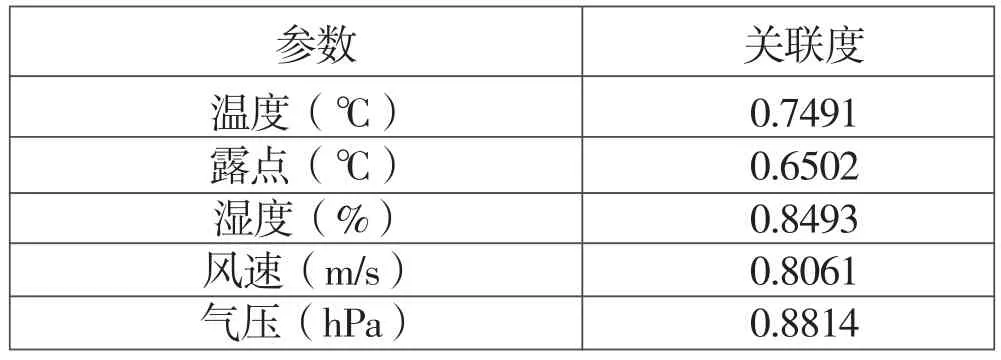
表1 灰色关联度
结果表明,各气象参数与负荷的关联度均大于0.6,说明各参数均与负荷有一定关联性,本文选择大于0.7的参数作为预测模型输入量。
3 负荷预测
3.1 评价参数
为准确评估预测模型性能,本文选择平均绝对误差(MAE)、平均平方根误差(RMSE)、平均绝对百分误差(MAPE)作为评价指标,其中ti为预测值,yi为实际值。MAE反映预测值与实际值的偏离情况,值越小,预测模型更精确。RMSE与原始数据具有相同的量纲,对异常值更敏感,值越小,预测更准确,MAPE采用百分率来说明误差的大小。计算方法如下。
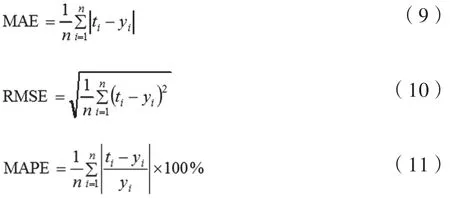
3.2 预测模型参数设置
预测模型输入节点数为4,输出节点数为1,隐层采用单层结构,同时设置不同的隐层神经元数量,为避免网络权值随机初始化影响,本文运行10次求平均值,结果如表2所示。
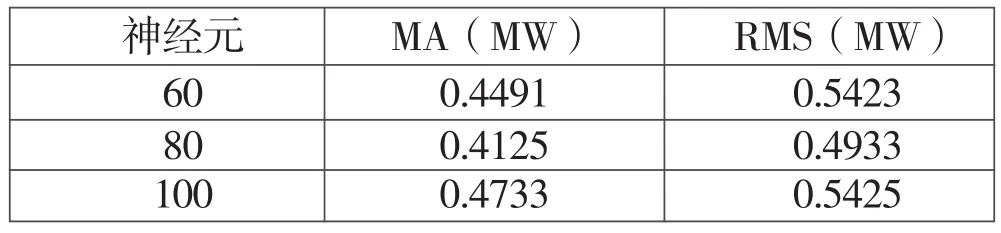
表2 隐含层神经元设置
深度学习中需多次训练才能得到较理想的结果,本文设置了多组Epoch,测试结果如表3所示。
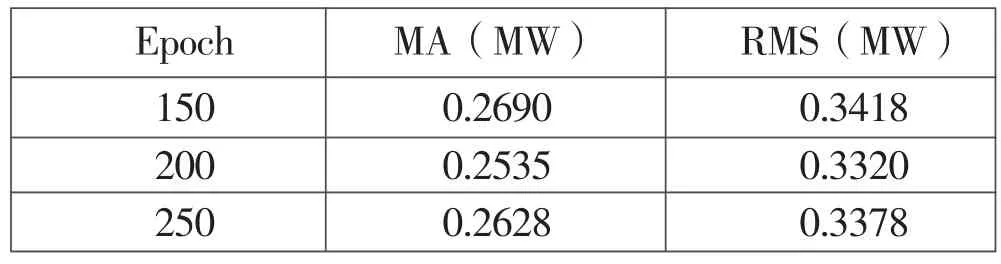
表3 Epoch设置
综上,本文隐层神经元个数选择80,Epoch设置为200,优化器选择Adam,Dropout设置为0.2。
3.3 预测结果评价及分析
本文对该农村负荷进行不同时间尺度预测,变化趋势与预测结果如图5、图6所示。
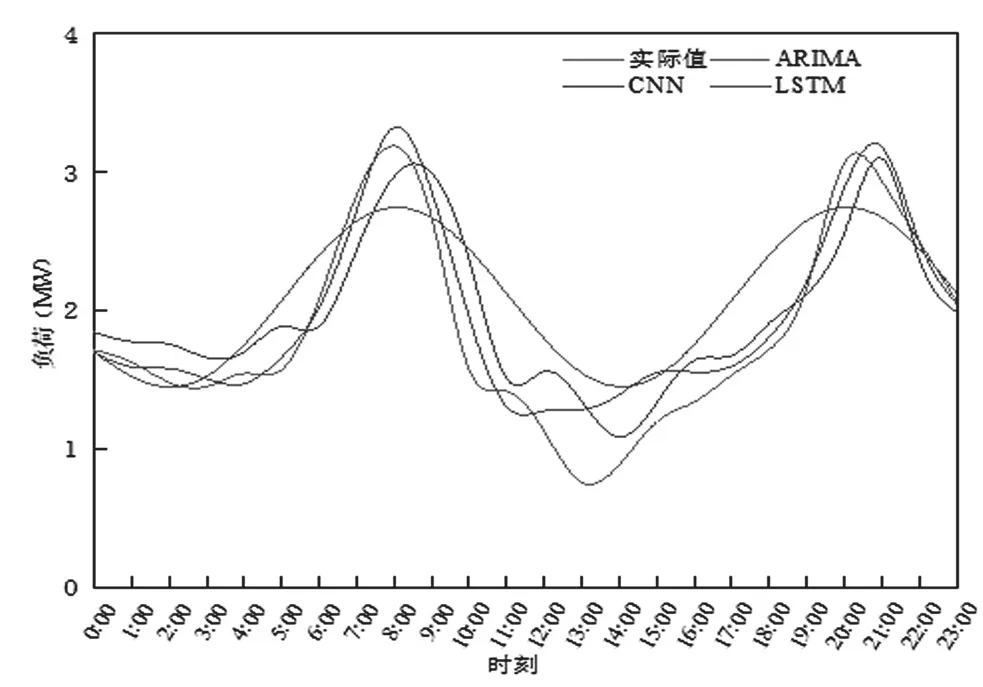
图5 日负荷预测
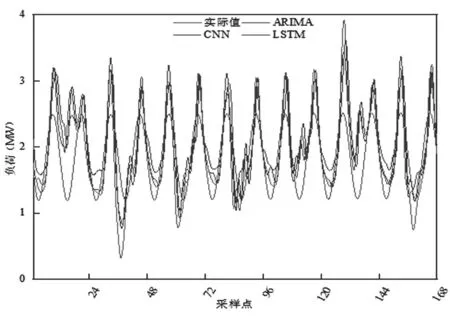
图6 周负荷预测
由表4知,以日负荷预测为例,相比ARIMA预测,CNN预测的MAE、RMSE、MAPE分别降低0.0626MW、0.0622MW、6.51%,LSTM预测的MAE、RMSE、MAPE分别降低0.176MW、0.211MW、12.26%。结果表明,三种预测模型精度由高至低依次为LSTM、CNN、ARIMA。
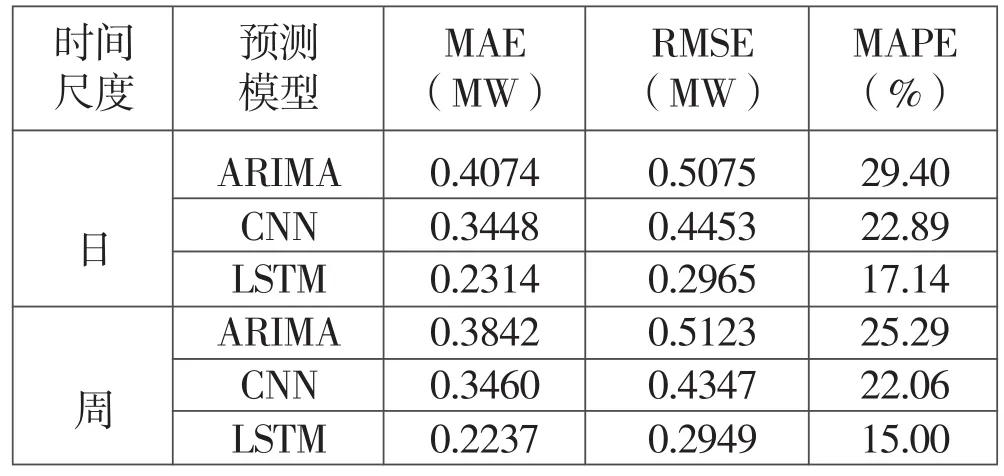
表4 预测结果评价
4 结束语
本文以陕西某农村变电站为研究对象,基于实际变电站的负荷数据结合神经网络算法实现不同时间尺度的负荷预测,得出以下结论。
1)以季节、周、日为量纲,对负荷进行特性分析,结果表明不同时间尺度下负荷的变化趋势存在差异,同时温度、湿度、风速、气压与负荷具有一定关联度。
2)建立ARIMA、CNN及LSTM预测模型,其中,LSTM预测精度最高,其预测日负荷时MAE为0.2314MW,RMSE为0.2965MW,MAPE为17.14%;预测周负荷时MAE为0.2237MW,RMSE为0.2949MW,MAPE为15.00%。
上述研究可供电力能源规划、可行性分析等方面提供支持,对电力系统的安全稳定经济运行有实际作用,具有一定推广性。
