基于SSA-BP神经网络的管道裂纹涡流识别研究*

王长新 陈金忠 辛佳兴 张雪伟 何仁洋 王德国

(1.中国石油大学(北京) 2.中国特种设备检测研究院 3.南昌航空大学)

0 引 言

管道运输是实现油气资源与市场高效结合的关键环节，在油气领域起着至关重要的作用。油气管道在制造、运输和服役等阶段易受外界环境、内部输送介质的冲击和腐蚀，以及人为因素的影响而出现裂纹或凹坑等多种缺陷，加之油气管道多处于条件恶劣及人员密集的厂区环境中，一旦发生泄漏事故可能造成人员伤亡和经济损失[1-5]。为了避免管道泄漏事故的发生，需对管道进行定期检测和维护，以保障管道安全有效运行[6-8]。

相对于传统的油气管道裂纹检测技术，涡流检测技术有着无需外加磁化和精度高的优点，且无需耦合剂，是实现管道裂纹检测的有效手段[9-12]。但由于管道检测里程长、检测数据量大，为快速准确掌握裂纹的分布情况以及尺寸识别，有必要对管道裂纹进行定量分析[13]。近年来，国内外学者对管道裂纹定量识别进行了大量研究[14]。LIU S.J.等[15]提取了金属管道裂纹的磁记忆检测信号,构建了BP神经网络，有效地定量识别出管道的裂纹参数。ZHANG H.等[16]采用IPSO-RBF神经网络对管道缺陷进行识别研究，提高了油气管道缺陷形态特征的识别精度。DAI Y.C.等[17]采用增加隐层神经元数量的方法对神经网络结构进行优化，提高了神经网络的训练精度，优化后的BP神经网络能够较好地识别出管道裂纹状态。WANG Z.W.等[18]通过数值模拟和试验研究，得到了裂纹深度、宽度与检测信号之间的关系，利用基于遗传算法的BP神经网络实现对裂纹的高精度反演。

目前，管道裂纹识别研究主要集中在漏磁检测领域[19]，针对管道裂纹涡流检测定量识别的研究较少，主要问题有：①裂纹尺寸较小，不易检出且外部干扰信号对裂纹检测影响较大；②缺乏对管道裂纹检测信号有效特征参数提取；③缺少高精度管道裂纹定量识别算法。本文基于SSA-BP神经网络对管道裂纹进行定量识别研究，运用Maxwell有限元仿真软件对不同尺寸裂纹进行数值模拟，探究不同尺寸裂纹信号特征的变化规律，并搭建基于涡流检测技术的裂纹检测系统，验证了数值模拟的正确性；对试验及数值模拟的检测信号进行特征参数提取，采用SSA-BP神经网络对裂纹参数进行定量识别。所得结果对油气管道裂纹定量识别技术的发展具有一定的指导意义。

1 数值模拟

1.1 涡流检测理论分析

涡流检测技术以铁磁性材料导体感应出的涡流为基础，通过测量相应的磁场变化得到缺陷信息。

涡流检测原理如图1所示。当激励线圈通入交变激励信号时，根据安培定律，线圈内部会产生交变一次磁场H1，假设该磁场在空间中一点处的磁感应强度为B1，其方向可由右手螺旋定则判断。根据法拉第电磁感应定律，当交变一次磁场H1作用于被测试件时，试件内部会产生感应涡电流I1，进而涡电流衍生出涡流磁场H2，其磁感应强度为B2。由于管道多为铁磁性材料，当线圈产生的一次磁场H1作用在试件表面时，试件内部磁畴朝着磁场H1的方向发生旋转，还会产生一个与一次磁场方向相同的磁化磁场H3，其磁感应强度为B3。在检测点A1处放置磁性芯片，此时磁性芯片在空间中检测到的复合磁感应强度B是B1、B1与B3的矢量和。B值可由式(1)确定。

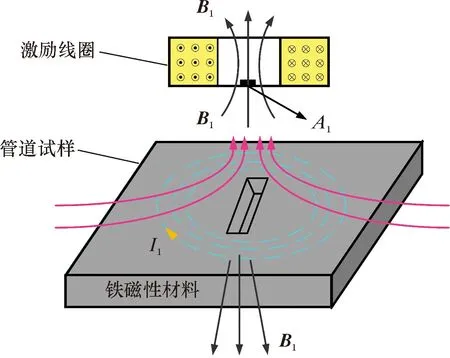
图1 涡流检测原理图Fig.1 Principle of eddy current detection

B=B1+B2+B3

(1)

式中：B1为交变一次磁感应强度，T；B2为涡流磁感应强度，T；B3为磁化磁感应强度，T。

当试件存在裂纹时，线圈激励的一次磁场不变，裂纹阻碍涡流形成回路，从而使涡流变大，涡流磁场随之增大；同时裂纹会削弱试件磁化，导致磁化磁场减小，由于涡流磁场和磁化磁场方向相反且磁化磁场远大于涡流磁场，所以磁化磁场将涡流磁场抵消。最后通过放置在A1处磁性芯片来获取复合场的磁信号并转化成直观的电信号进行分析，通过电信号的差异来判断被测试件的裂纹尺寸。

1.2 有限元模型

由于管道曲率相对于探头尺寸较小，所以利用平面代替管道弧面进行仿真分析，建立简化的三维管道裂纹涡流检测模型，如图2所示。

图2 管道裂纹涡流检测三维模型Fig.2 Three-dimensional model of pipeline crack identification from eddy current detection

模型主要包括激励线圈、裂纹、试件及空气域。将试件材料设置为X52管材，经过仿真优化及考虑试验中芯片封装的影响，最终将激励线圈尺寸设置为内径9 mm，外径11 mm，高度5 mm，匝数200。激励电流信号幅值为0.1 A，频率为500 Hz。

1.3 裂纹深度与仿真信号关系

设置7条不同深度的裂纹，长度20 mm，宽度1 mm，深度0.2～0.8 mm(步长0.1 mm)，相邻裂纹间距35 mm。在实际工程中考虑探头外壳以及芯片封装的影响，将提离高度设置为0.5 mm，激励线圈沿X正方向扫描，提取A1点的磁通密度Z向分量幅值，截取扫描路径上各裂纹的仿真信号，结果如图3所示。

图3 不同深度裂纹仿真信号Fig.3 Simulation signals of cracks with different depths

由图3可以看出：激励线圈在无裂纹区域时仿真信号近似呈一条水平直线，信号分布与试件表面形貌一致；通过裂纹区域时仿真信号发生明显突变，呈现“近V字形”；波峰值随着深度的增加出现小幅度增加，波谷值随着深度的增加而减小，但减小速率逐渐减缓，信号峰峰间距无明显变化。

1.4 裂纹宽度与仿真信号关系

设置7条不同宽度的裂纹，长度100 mm，深度3 mm，宽度1.0～4.0 mm(步长0.5 mm)，相邻裂纹间距80 mm。将提离高度设置为0.5 mm，激励线圈沿X正方向扫描，提取A1点处的磁通密度Z向分量幅值，截取扫描路径上各裂纹的仿真信号，结果如图4所示。

图4 不同宽度裂纹仿真信号Fig.4 Simulation signals of cracks with different widths

由图4可知：激励线圈在无裂纹区域时仿真信号近似呈幅值为0的水平直线，通过裂纹区域时仿真信号出现不同程度突变；裂纹宽度对信号峰峰间距影响较为明显，宽度越大峰峰间距随之变大；波峰值随着宽度的增加呈现递增的趋势；波谷值随着深度的增加而减小，但减小速率逐渐降低。

2 试验验证

2.1 试验平台

为验证仿真结果的正确性，搭建裂纹涡流检测试验系统，对不同尺寸裂纹进行试验验证，试验探头及裂纹参数与仿真一致。试验系统组成如图5所示，主要包括激励模块、检测模块、信号调理模块、数据采集模块、上位机软件和PC机。

图5 试验系统构成图Fig.5 Composition of test system

激励模块采用BP 4610信号发生器，产生幅值为0.1 A、频率为500 Hz的正弦交流信号并通过导线传递至激励线圈。检测模块由探头、三轴联动滑台和试件组成，用于检测试件表面的磁场信号。三轴联动滑台固定并驱动探头实现在试件上方路径扫描运动，位于检测探头底部圆心位置处的TMR传感器(敏感方向Z轴)将提取到的磁场信号转化成电压信号输出至调理电路，调理电路对电压信号进行放大滤波处理。数据采集模块包括采集卡和采集程序，经过放大滤波处理后的电压信号由采集卡转变为数字信号传输至采集程序中。最终电脑端对采集到的数据进行分析处理。

2.2 裂纹深度与检测信号关系

探头沿不同深度裂纹试件上方0.5 mm处路径扫描，提取检测电压信号峰值，截取各裂纹的检测信号，结果如图6所示。

图6 不同深度裂纹检测信号Fig.6 Detection signals of cracks with different depths

分析图6可知，由于试验台在运行过程中存在不同程度的振动以及受试件表面粗糙度的影响，检测信号在无裂纹区域的稳定性欠佳，但裂纹区域的检测信号较为稳定。波峰值随着裂纹深度的增加而小幅度上升，在深度0.2～0.4 mm阶段波峰值呈现微增长趋势，深度0.5～0.8 mm阶段波峰值增长速率极为缓慢，在深度0.8 mm区域达到顶峰(2.274 V)；波谷值随着裂纹深度的增加而减小，且减幅逐渐变小，在深度0.2～0.3 mm阶段减幅最大(0.102 00 V)，在深度0.7～0.8 mm阶段减幅最小(0.000 86 V)，在深度0.8 mm区域降至最低(2.173 40 V)；检测信号峰峰间距无明显变化。针对波峰值和波谷值的增长、减小速率由快到慢的现象，分析原因是受趋肤效应的影响，随着深度的增加，电流密度呈指数衰减，深层裂纹检测信号的分辨率有所下降。

2.3 裂纹宽度与检测信号关系

探头沿不同宽度裂纹试件上方0.5 mm处路径扫描，提取检测电压信号峰值，截取各裂纹的检测信号，结果如图7所示。

图7 不同宽度裂纹检测信号Fig.7 Detection signals of cracks with different widths

图7表明:探头在无裂纹区域时检测信号趋于平缓，峰峰间距和波峰值均随着裂纹宽度的增加出现不同程度的增长，但增幅逐渐减小;宽度1 mm时峰峰间距和波峰值最小，分别为2.749 mm和2.268 V;宽度4 mm时峰峰间距和波峰值最大，分别为5.500 mm和2.438 V。波谷值与裂纹宽度呈负相关的非线性变化规律，且变化趋势逐渐减缓。在宽度1.0～2.5 mm阶段波谷值出现明显降低，由2.147 V降至1.866 V，平均降幅为4.57%；在宽度3.0～4.0 mm阶段波谷值出现小幅度降低，由1.822 V降至1.747 V，平均降幅为2.08%，比上一阶段减少2.490%。针对峰峰间距和波峰值随裂纹宽度的增加，其增长速率逐渐变小，及波谷值随裂纹宽度的增加，其减小速率逐渐降低的现象，分析原因是随着裂纹宽度与探头尺寸的比例增大，能够到达裂纹边缘的磁场减少，对复合磁场的影响相应减小，进而导致裂纹检测信号分辨率降低。

2.4 试验结果与仿真结果对比

对仿真信号与试验信号进行归一化处理，结果如图8所示。由图8可以看出，仿真与试验所得到的信号趋势基本一致。

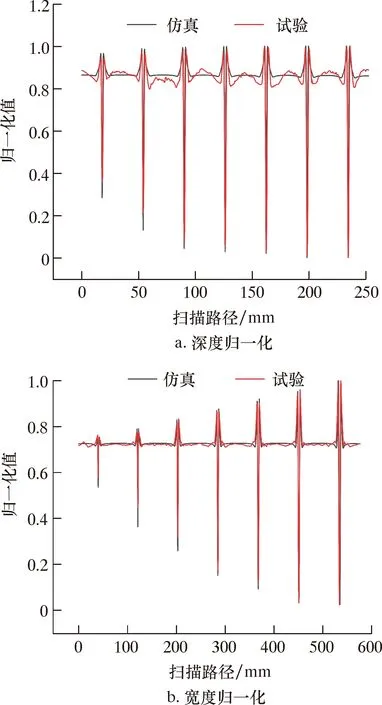
图8 归一化处理结果对比图Fig.8 Comparison of normalization results

为验证仿真的正确性，对仿真结果与试验结果进行定量对比分析。定义偏差δ为衡量指标。

(2)

式中：B为各裂纹仿真信号幅值与试验信号幅值之比；A为各裂纹仿真信号幅值与试验信号幅值之比的均值。

将归一化数值代入，结果如表1和表2所示。表1和表2中的数值(信号幅值)均为归一化后的数值。

表1 不同深度裂纹偏差对比Table 1 Comparison of deviations for cracks with different depths

表2 不同宽度裂纹偏差对比Table 2 Comparison of deviations for cracks with different widths

由表1和表2可知：不同深度裂纹信号偏差在一定范围内浮动，最大不超过5.240%，平均偏差为2.219%；不同宽度裂纹偏差均小于1.000%，且最低至0.100%，平均偏差为0.443%。通过仿真与试验比值偏差的定量对比分析，验证了仿真的正确性。

3 基于SSA-BP神经网络的裂纹定量识别

3.1 特征参数及样本库的选取

裂纹信号的定量识别与其特征参数的选取密切相关，通过仿真与试验涡流检测信号的对比分析，结合BP神经网络的特点，本文采用基谷值(Bg)、峰峰值(Bz)、周长(C)和面积(S)作为管道裂纹信号的特征参数，如图9所示。

图9 特征参数提取示意图Fig.9 Schematic diagram of extraction of characteristics parameters

由于TMR芯片为线性磁场传感器，所以相同裂纹尺寸下试验值和仿真值存在如下比例关系。

(1)基谷值比例系数K1。K1=V1/(Bj-Bmin),其中V1为试验信号基谷值，Bj为仿真信号基线值，Bmin为仿真信号谷值。

(2)峰峰值比例系数K2。K2=V2/(Bmax-Bmin),其中V2为试验信号峰峰值，Bmax为仿真信号峰值，Bmin为仿真信号谷值。

(3)周长比例系数K3。

对不同深度和宽度尺寸裂纹对应的比例系数进行均值处理，得到比例系数与裂纹深度、宽度的对应关系，结果如表3所示。

表3 比例系数与裂纹深度、宽度尺寸对应关系Table 3 Corresponding relationship between proportional coefficients and crack depths and widths

为降低加工精度对预测结果的影响，同时获得足够的训练样本，按照表3的对应关系将仿真数据与试验数据进行等比例换算，将换算后的134组数据作为神经网络的训练样本，14组数据作为测试样本。测试样本特征参数如表4所示。

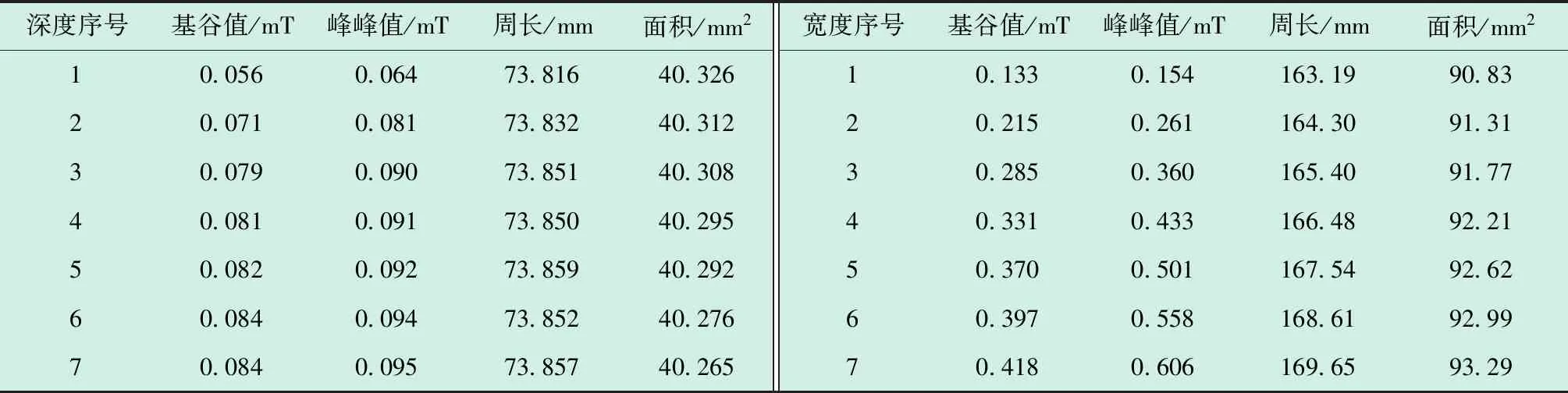
表4 测试样本特征参数Table 4 Characteristics parameters of test sample

3.2 SSA-BP神经网络

BP神经网络由输入层、隐藏层和输出层3部分组成，其网络结构如图10所示。

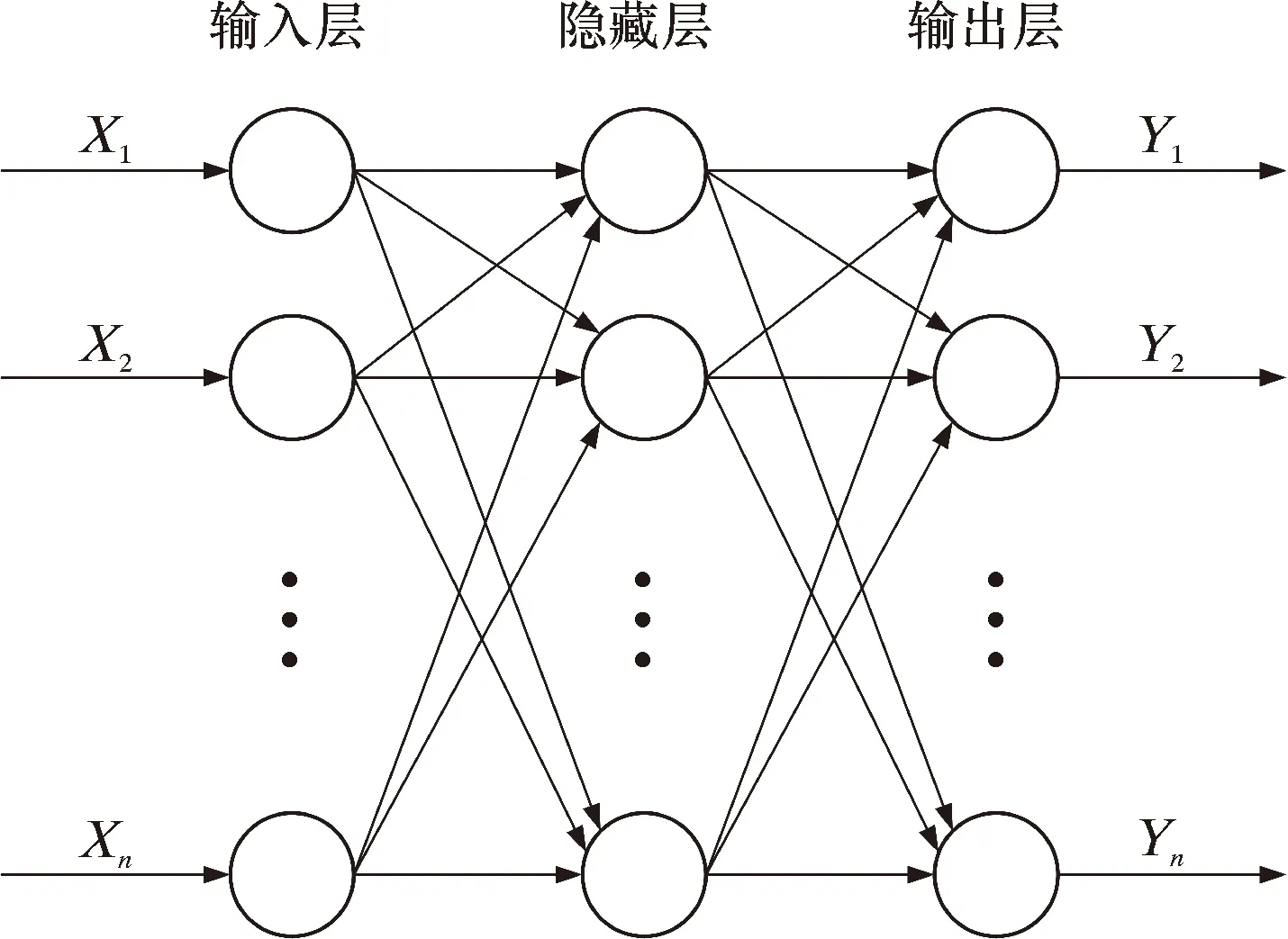
图10 BP神经网络结构图Fig.10 Structure of BP neural network

BP神经网络的学习过程由信息的正向传播和误差的反向传播组成，其通过调节网络参数以实现网络的实际输出向期望输出逼近。但在BP神经网络中，神经单元的权值和阈值随机产生，为避免求解过程中随机权值和阈值对识别精度和运行效率的影响，本文将麻雀搜索算法[20]和神经网络相结合，采用麻雀搜索算法优化BP神经网络的权值和阈值，以此获得较高的识别精度。以基谷值、峰峰值、周长和面积为输入，裂纹的深度或宽度为输出，建立SSA-BP神经网络裂纹定量识别模型。SSA-BP神经网络裂纹定量识别模型的流程如图11所示。

图11 SSA-BP神经网络裂纹定量识别模型流程图Fig.11 Flow chart of SSA-BP neural network model for quantitative crack identification

3.3 裂纹定量识别结果与分析

为验证特征参数与算法的可靠性和实用性，将134组训练样本和14组测试样本(见表4)作为SSA-BP神经网络模型的样本集，对仿真数据和试验数据进行预测，预测结果和相对误差分别如图12和图13所示。

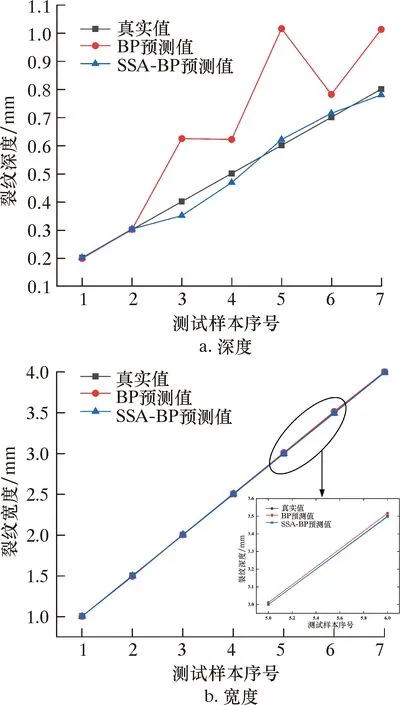
图12 预测结果对比Fig.12 Comparison of prediction results

图13 相对误差对比Fig.13 Comparison of relative errors

由图12、13可以看出，传统BP神经网络出现较大的测试误差，深度最大绝对误差为0.42 mm，最大相对误差为69.23%；宽度最大绝对误差为0.017 mm，最大相对误差为0.61%，对裂纹宽度的识别精度尚可，但对裂纹深度的识别精度欠佳；采用SSA-BP神经网络预测,深度最大绝对误差为0.05 mm，最大相对误差为12.53%；宽度最大绝对误差为0.004 3 mm，最大相对误差0.25%；较传统BP神经网络，SSA-BP神经网络深度、宽度最大相对误差分别减小56.7百分点和0.36百分点，对裂纹深度和宽度的识别精度显著提高。

4 结 论

(1)基于涡流测试技术，采用数值模拟方法研究了裂纹尺寸对涡流检测信号的影响规律，搭建了裂纹涡流检测试验系统，对裂纹涡流检测的可靠性和准确性进行验证。研制的涡流检测探头可实现对宽1 mm、深0.2 mm的裂纹有效检出。

(2)针对传统BP神经网络识别精度低和收敛慢的缺点，采用麻雀搜索算法优化BP神经网络，提高了神经网络的识别精度和运行速度。构建的SSA-BP神经网络管道裂纹识别模型较传统BP神经网络模型，深度、宽度最大相对误差分别减小56.7个百分点和0.36个百分点，深度和宽度最大绝对误差分别为0.05和0.004 3 mm，能够有效实现对管道裂纹尺寸的定量识别。