水力压裂过程中直井段B环空水泥环完整性分析*

曾 波 王 冬 宋 毅 连 威 李 军,4

(1.中国石油西南油气田公司 2.四川长宁天然气开发有限责任公司 3.中国石油大学(北京)克拉玛依校区 4.中国石油大学(北京))

0 引 言

页岩气井开发过程中井筒环空带压现象严重，重庆涪陵页岩气区块多口井发生环空带压现象，四川威远长宁页岩气示范区N209、N210及N203等井也发生了不同程度的环空带压现象，严重影响了页岩气井的井口安全和生命周期[1-2]。根据齐奉忠等[3]对某页岩气区块160多口页岩气井环空带压情况的调研，压裂前环空带压井比例略高于10%，但压裂后环空带压井的比例激增至50%以上，表明页岩气井环空带压现象和水力压裂有明显关联。

页岩气井环空带压会对油气的安全开采构成威胁，严重时会导致关井甚至全井报废，将带来巨大的经济损失，因此，有必要对页岩气井生产过程中环空带压的机理进行研究。席岩等[4]对力-热耦合作用下水平段水泥环的完整性进行了研究，认为力-热耦合作用下水泥环内壁应力大幅提升，加剧了水泥环失效的风险；朱海燕等[5]对水力压裂过程中射孔处微环隙的产生和扩展进行了分析，认为只要第一界面或者第二界面的胶结强度小于地层的抗拉强度，那么井眼周围均会产生微环隙；C.KOSINOWSKI等[6]研究了射孔作业对水泥环密封完整性的影响，认为较高硬度的水泥石在经受多次压裂以后，其内部可能产生横向裂纹；T.PETERSEN等[7]对套管偏心条件下胶结面的失效机理进行了试验，结果表明，热循环条件下套管偏心程度越高，胶结面越容易失效，偏心度会显著增加水泥环失效的风险。以上学者的研究都关注了水平段水泥环的完整性，并没有对直井段水泥环的完整性进行研究，直井段水泥环作为环空二级屏障[8]，保证其完整性具有重要意义。因此，本文基于页岩力学参数剖面和地应力参数剖面，建立不同开次下的套管-水泥环-地层有限元模型，结合摩尔库伦准则对直井段水泥环的完整性进行判断，并对影响水泥环完整性的因素进行敏感性分析。研究成果对环空带压的控制具有借鉴作用。

1 数值模型建立及验证

1.1 井身结构

图1为某页岩气井井身结构图。技术套管与油层套管之间的环空为B环空，该井压裂前未出现环空带压，压裂后则出现了明显的B环空带压现象[9-10]，可以判断地层气体穿透直井段水泥环到达井口，因此有必要对直井段水泥环的应力状态以及完整性进行分析。

图1 某页岩气井井身结构Fig.1 Wellbore structure of a shale gas well

一级导管下入井深30 m，二级导管下入井深160 m，一开套管下入井深950 m，二开套管下入井深2 350 m，造斜点井深2 200 m。各开次套管及钻头尺寸如表1所示。根据表1中套管及钻头的尺寸即可确定不同井深处对应的近井筒有限元模型的尺寸。

表1 各开次套管及钻头尺寸 mmTable 1 Casing and bit size of each spudding mm

1.2 有限元模型

鉴于直井段三维有限元模型网格数量过多，运算效率慢，时间成本高，本文利用二维平面有限元模型代替三维有限元模型。对不同开次的井身结构建立对应的有限元模型。一级导管、二级导管、一开、二开对应的有限元模型如图2所示。

图2 不同开次对应的有限元模型Fig.2 Finite element model corresponding to different spuddings

为了消除尺寸的影响，设置地层尺寸为井眼尺寸的10倍。套管和导管的弹性模量为210 GPa，泊松比为0.3；水泥环的弹性模量为8 GPa，泊松比为0.15；在地层岩石力学参数设置方面，可按照岩石力学参数剖面设置不同井深对应的岩石力学参数。在边界条件设置方面，套管、水泥环、地层以及导管之间的界面采用绑定接触的方式进行约束，其参数参考文献[10]，同时对地层外边界进行位移约束。在载荷设置方面，由于套管内压和地应力都与井深有关，可按照套管内压剖面和地应力剖面对模型施加套管内压和地应力，即可得到不同井深对应的有限元模型。

1.3 水泥环破坏准则

水泥环为脆性材料，其主要失效形式有受拉破坏和受压破坏2种。拉伸载荷作用下水泥环易产生拉伸破坏，压缩载荷作用下水泥环易产生压缩破坏或塑性屈服[11-12]。当水泥环受单向拉伸/压缩载荷时可用最大主应力准则判断水泥环是否被破坏，但是井下水泥环一般同时受径向压缩载荷与周向拉伸载荷的共同作用，这时一般采用摩尔库伦准则对水泥环的失效情况进行判定，如表2所示。根据前人的研究，柱坐标系下σ1=σθ，σ3=σr，其中σθ和σr分别为水泥环的切向和径向应力，MPa。

表2 Mohr-Coulomb破坏准则Table 2 Mohr-Coulomb failure criterion

表2中：σ1、σ3分别为水泥环中最大、最小主应力，MPa；σt为水泥环抗拉强度，MPa；σc为水泥环抗压强度，MPa。

1.4 模型验证

为了证明上述数值计算模型的准确性，结合陶谦等[9]建立的全尺寸水泥环密封能力评价装置和相关的试验结果进行验证，如图3a所示。验证的基本原理为：利用套管、水泥环和外筒模拟压裂过程中套管-水泥环-地层组合体，然后通过压力系统向套管内周期加载/卸载压力，以模拟压裂过程中套管内压周期性变化。外筒与水泥环、水泥环与套管界面之间存在应力传感器，用以监测加载/卸载过程中水泥环的受力状态。套管的尺寸为：外径139.7 mm，内径124.3 mm，高度1 200 mm；外筒外径244.5 mm，内径193.7 mm，高度1 200 mm，内筒钢级P110，外筒钢级N80，弹性模量210 GPa，泊松比0.3。外筒和套管之间水泥环的弹性模量14.3 GPa，泊松比0.12，抗拉强度3.5 MPa，抗压强度40.5 MPa。

对套管内施加70 MPa循环内压模拟压裂施工，试验结果表明：常规水泥石在套管膨胀的作用下承受较高的周向拉应力，产生径向拉伸裂纹，最终导致水泥环失效。

为了验证前文有限元模型的准确性，建立套管-水泥环-外筒组合体二维有限元模型。套管-水泥环-外筒的几何及力学参数与试验相同，套管-水泥环-外筒组合体有限元模型及计算结果如图3所示。

图3 有限元计算结果与试验结果对比Fig.3 Comparison between finite element calculation results and experimental results

试验过程中，当套管内压加载至70.0 MPa时，水泥环外壁径向压应力为22.3 MPa，周向拉应力为4.2 MPa；数值模型计算结果显示，套管内压为70.0 MPa时，水泥环外壁径向压应力为20.4 MPa，周向拉应力为4.2 MPa。径向压应力的相似度为91.5%，周向拉应力的相似度为99.5%，综上可知建立的数值计算模型准确可靠。

2 实例分析

2.1 地应力和岩石力学参数剖面

川渝地区页岩气成藏过程中地质构造活跃，纵向岩性复杂，矿物成分变化大，多种岩性交错互层且多套孔隙压力体系并存，导致地应力剖面较为复杂[13]。图4和图5分别为此井地应力和岩石力学参数剖面。从图4可以看出，垂向地应力、水平最大地应力随井深的增加而增大但波动范围较小，水平最小地应力随井深的增加而增大且波动范围较大。图5中，岩石弹性模量在压实作用下随着井深的增加而增大，在井深500 m附近岩石的弹性模量有较大突变，主要是因为蓬莱镇组和须家河组交界处岩性变化较大。泊松比所表现的趋势则与弹性模量所表示的趋势相反，泊松比随着井深的增加逐渐减小，因为压实作用下岩石逐渐致密，变形能力逐渐降低。

图4 地应力剖面Fig.4 In-situ stress profile

图5 岩石力学参数剖面Fig.5 Rock mechanical parameter profile

2.2 套管有效内压

套管有效内压计算如式(1)所示：

pin=pwh+ph-Δps

(1)

式中：pin、pwh、ph、Δps分别为套管有效内压、井口泵压、压裂液静水压力以及沿程摩阻，MPa。

由于本文研究对象为页岩气井直井段，沿程摩阻远小于井口泵压与压裂液静水压力之和，为简化计算过程,忽略沿程摩阻的影响。压裂过程中井口泵压为85 MPa，压裂液密度取1 000 kg/m3。

2.3 结果与讨论

基于前文中井身结构、地应力、岩石力学参数剖面以及套管有效内压，可以计算不同井深处B环空水泥环的周向应力、径向应力以及摩尔库伦准则判定值，结果如图6所示。

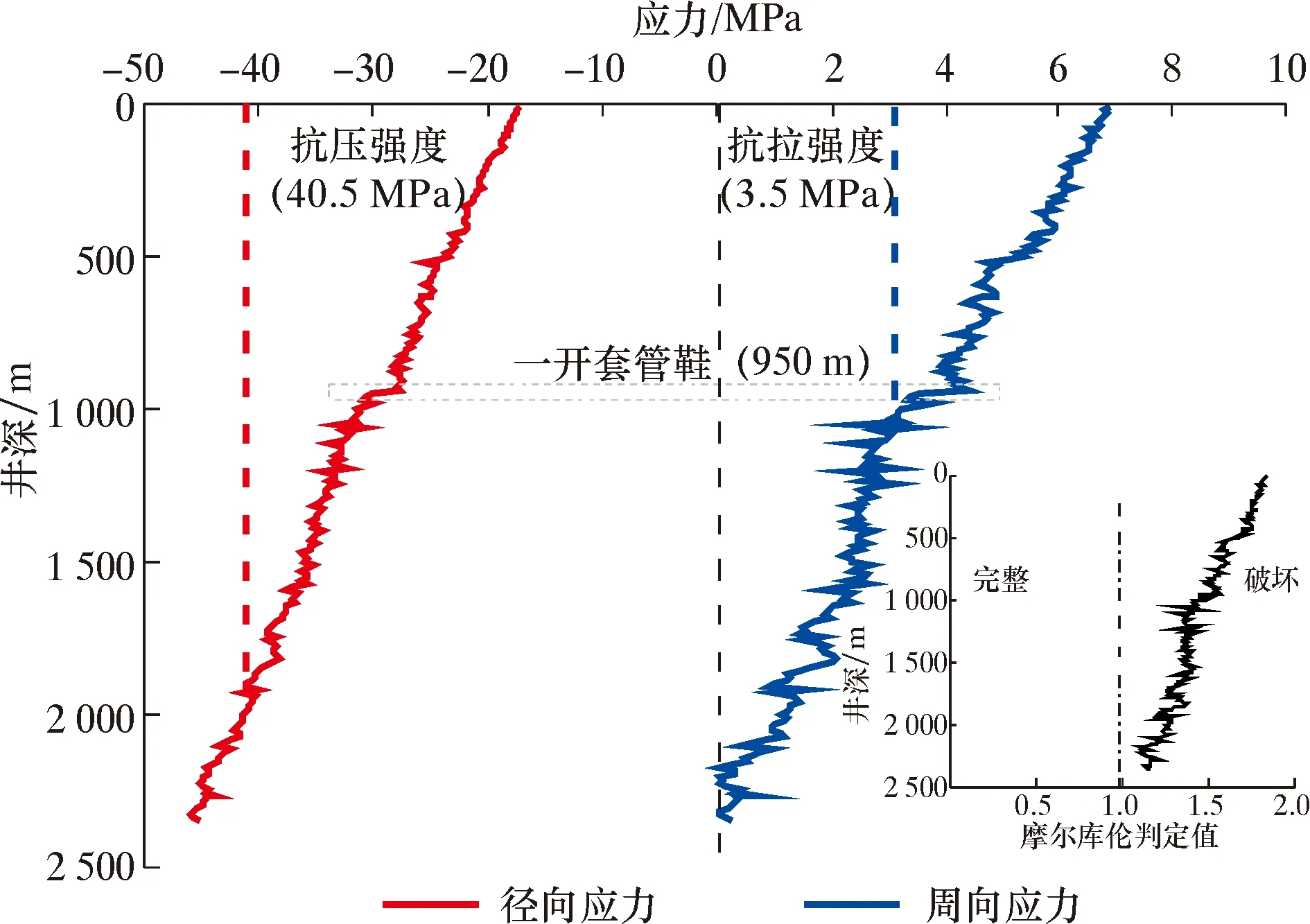
图6 B环空水泥环最大周向应力、径向应力及摩尔库伦判定值计算结果Fig.6 Calculation results of maximum circumferential stress,radial stress and Mohr-Coulomb criterion value for annulus B

由6可知：B环空水泥环最大径向应力为负，表明水泥环内壁在径向上受压；最大周向应力为正，表明其在周向上受拉[14]。最大径向应力随着井深的增加不断增大，因为地应力与套管有效内压随井深的增加而增大，水泥环的受压程度逐渐增大。最大周向应力随着井深的增加而不断减小，因为地应力随井深的增加速度大于套管内压随井深的增加速度，地应力对近井筒组合体的“包裹”作用强于套管内压对井筒组合体的“膨胀”作用。

当井深小于一开套管鞋对应的井深时，摩尔库伦判定值大于1，水泥环的主要失效形式为周向拉伸失效。由于一开较二开多一层表层套管以及水泥环，导致地应力难以传递到B环空水泥环，无法平衡套管内压引起的周向拉应力，所以一开套管鞋以上位置处的水泥环容易产生周向受拉失效。当井深继续增加时，水泥环则主要承受径向压应力且其值不断增加，存在径向压缩失效的风险。

直井段水泥环的摩尔库伦判定值都大于1，说明压裂过程中水泥环存在失效的风险，地层中的高压气体可能沿着二开套管鞋向上运移至井口，导致B环空带压。

2.4 影响因素敏感性分析

2.4.1 水泥环弹性模量

水泥环弹性模量是控制油气井井筒完整性的重要参数之一，一般认为固井水泥环的理想特性为“高强度、低刚度”[15-19]，但以往并未研究水泥环弹性模量对整个直井段水泥环完整性的影响，在前文计算的基础上保持其他参数不变，设置水泥环的弹性模量分别为4、6、8和10 GPa，计算结果如图7所示。

图7 不同弹性模量条件下B环空水泥环应力分析Fig.7 Stress analysis of cement sheath of annulus B with different elastic modulus

由图7可知:使用低弹性模量水泥浆体系可以显著降低B环空水泥环的周向应力和径向应力；随着井深的增加，一开套管鞋以下水泥环的周向应力逐渐趋于相等，一开套管鞋以上水泥环的周向应力对弹性模量的变化则更为敏感。水泥环径向应力在一开套管鞋处发生明显变化，主要是套管层次发生变化导致水泥环的受力状态不同，同时可以看出水泥环的弹性模量越低，其径向应力减小幅度越大。因此，有必要在直井段尤其是一开套管鞋以上位置,使用低弹性模量的水泥浆体系，以防止水泥环被破坏。

2.4.2 水泥环泊松比

为了增加水泥石的弹韧性，固井之前一般会向水泥浆中添加一定量的乳胶、纤维等弹韧性材料，这导致不同体系水泥浆的泊松比具有明显差异[20]。在前文计算的基础上保持其他参数不变，设置水泥环的弹性模量为4 GPa，泊松比分别为0.10、0.15、0.20和0.25，井口泵压为85 MPa，计算结果如图8所示：

图8 不同泊松比条件下B环空水泥环应力分析Fig.8 Stress analysis of cement sheath of annulus B with different Poisson’s ratios

由图8可知，水泥环周向应力受泊松比影响较大。增加泊松比能明显减小水泥环的周向应力，甚至使一定井深位置处的周向应力由受拉变为受压。一开套管鞋以上水泥环的径向应力有所区别，以下位置则几乎不受泊松比的影响。摩尔库伦判定值显示，水泥环具有高泊松比特征时有利于水泥环的完整性，因此，增加水泥环的泊松比有利于保障其完整性。

2.4.3 井口泵压

页岩岩石非均质性强，不同压裂段内页岩的起裂压力存在较大差异。实际压裂过程中，井口泵压会有所不同，有必要研究不同泵压条件下水泥环的应力状态。设置水泥环的弹性模量为4 GPa，泊松比0.2，泵压分别为75、85、95、105和115 MPa，计算结果如图9所示。

图9 不同井口泵压条件下B环空水泥环应力分析Fig.9 Stress analysis of cement sheath of annulus B with different wellhead pump pressures

由图9可以看出，不同井口泵压条件下B环空水泥环的周向应力、径向应力以及摩尔库伦判定值曲线基本平行，井口泵压对周向应力的影响更为明显，井口泵压越大，水泥环受周向拉伸失效的风险越高。因此，有必要在压裂作业过程中采取技术手段降低页岩的起裂压力，为水泥环的完整性提供保障。

3 结 论

通过建立页岩气井不同开次条件下套管-水泥环-地层组合体数值模型，计算压裂过程中直井段B环空水泥环径向、周向压力，并利用摩尔库伦准则对水泥环完整性进行判定，得到如下结论：

(1)压裂过程中水泥环最大径向应力随着井深的增加不断增大，最大周向应力随井深的增加则逐渐减小，甚至由受拉变为受压；表层套管鞋以上的水泥环易发生周向拉伸破坏，以下位置的水泥环则易发生径向压缩破坏。

(2)降低水泥环弹性模量可以降低水泥环的周向、径向应力以及摩尔库伦判定值，增加水泥环泊松比有利于降低水泥环的周向应力，但对径向应力影响较小，因此使用低弹性模量、高泊松比的水泥浆体系有利于保障水泥环的完整性。

(3)不同井口泵压条件下水泥环的周向、径向应力以及摩尔库伦判定值剖面基本平行，降低井口泵压有利于保障水泥环的完整性，压裂作业过程中应采取技术手段降低页岩的起裂压力。