基于分支定界算法的应急疏散选址方法

马国普，徐俊韬

（陆军勤务学院，重庆 401311）

0 引言

中国幅员辽阔，是重大突发事件发生最频繁的国家之一。国家就重大突发事件建立的应急保障机制与所需的保障力相比仍有差距。突发事件造成的破坏和损失巨大，事件中的人员转移和安置一直是非常重要的问题。

目前，重大突发事件应急疏散研究较少把后方安置点与前线救援点联系起来考虑人员转移和物资运输。人员转移是从事件发生点先转移到前线救援点，再转到安置点，而物资运输是从安置点运输到救援点，再从救援点运输到事件发生点。如果救援需求没有得到满足，会造成重大损失，但如果物资供应远远大于需求，同样也是一种经济损失。事件初期并不能完全把握住需求，只能通过场景加概率，大致推算出预期需求，由地区政府提供预算资金。本文的目标是在预算范围之内最小化未被转移的人数，同时尽可能满足救援物资的需求。

1 突发事件人员疏散模型

1.1 突发事件中人员转移分析

在重大突发事件中，洪水是一类典型灾害，下文以洪灾为例进行问题分析。洪灾中受灾点区域的大多道路被水淹没，陆地交通工具不能直接进入，所以要在事件发生点附近设置救援点，在这里转换成水路交通工具进行物资和人员的输送，依此提出“受灾点-救援点-安置点”概念模型。在确定场景的情况下，每个事件发生点的物资需求量、受灾人数和伤病人员数量可以估算，并且安置点的人口容量也是确定的，预置安置点的预置成本也可以估算。在转移过程中，不仅要考虑这些，还要考虑运输过程中安置点到救援点运输工具的容量，及救援点到受灾点的运输工具容量等。在实际情况中，由于很多未知条件的限制，对灾区需求和受灾人员数量的评估有一定的误差，在此就需要使用情景与概率结合的分析方式减小误差，得出不确定需求情况下的分析方案。

1.2 最佳安置点的确定

临时安置点的选择需要考虑安置点容量、转移到安置点的距离、安置点的成本等影响因素。

1.2.1 影响因子

影响人员转移过程中临时安置点的确定因素很多，主要有总预算、运输工具的有效运量、运输工具单位时间成本、救援品费用，安置点选址费用、运输工具总量、运输工具工作时长、安置点到救援点的距离、救援点到受灾点的距离、安置区的容量等因素。

1.2.2 场景的设置

根据以往洪灾统计数据情况，先综合根据各个受灾点的受灾情况、人口、道路环境、地理位置等因素生成一种需求场景1。让每个受灾点的需求与位于［1.0，1.5］的一个随机数相乘，这样可以得到一种灾情偏重的场景2。再将随机数的生成区间改成［0.5，1.0］，将场景1 的需求乘以随机数，得到一种灾情偏轻的场景3。将各场景概率依次设置为0.4，0.3，0.3。

1.3 应急疏散优化模型

1.3.1 模型相关假设

抗洪抢险中人员疏散作如下假设：

1）假设运输工具为匀速；2）不考虑人员在运输中的伤亡；3）运输工具为灾前配置，不计入预算；4）在人员运输方面仅只考虑数量因素；5）运输过程中道路看成通畅状态；6）不考虑运输救援人员的问题；7）设定人员在两段路程的运输中是相等的，没有在救援点不转移的人。物资运输也采用同类假设。

1.3.2 模型参数说明

模型构建所使用的参数较多，这里统一进行参数符号说明。

1）基本参数

I：临时安置点集合，i∈I；J：受灾点集合，j∈J；K：灾区所需救援品集合，k∈K；F：救援点集合，f∈F；M：安置点运输工具类型集合，m∈M；M：救援点运输工具类型集合，m∈M；ξ：灾情情景集合，δ∈ξ。

2）与情景不直接相关的参数

B：总预算费用（元）；W：临时安置点i 的容量（人）；Q：单台m 型运输工具的有效运量（kg 或人）；C：单台m 型运输工具运行单位时间所需成本（元）；e：安置点选址费用（元）；S：救援品在安置点i 的总量（kg）；C：采办救援品的单位费用（元）；T：m 型运输工具有效时长（h）；V：i 点m 型运输工具总量（台）；V：f 点m 型运输工具总量（台）；V：m 型运输工具的速度（km/h）；L：安置点i 到救援点f 的距离（km）；L：救援点f 到受灾点j 的距离（km）；x：1表示选定临时安置点，0 表示不选。

3）与情景直接相关参数

k：受灾点j 的物资需求量（kg）；K：用m 型运输工具运输到受灾点j 的物资量（kg）；d：受灾点j的受灾人员数量（人）；D：用m 型运输工具转移到受灾点j 的受灾人员数量（人）；t：m 型运输工具从救援点f 到受灾点j 的时间（h）；t：m 型运输工具从安置点i 到救援点f 的时间（h）；V：m 型运输工具从救援点f 到受灾点j 的运输次数（次）；V：m型运输工具从安置点i 到救援点f 的运输次数（次）；U：m 型运输工具从受灾点j 到救援点f 的运输次数（次）；U：m 型运输工具从救援点f 到安置点i 的运输次数（次）；q：未满足物资需求的惩罚因子（人/kg）；A：在受灾点j 未能转移的受灾人员数量（人）；G：受灾点j 未能满足的物资需求量（kg）；P：情景概率，P∈P。

1.3.3 优化模型构建

Aruna Apte 的数学模型在各种抗灾救援运输建模中被广泛应用。但是，经典模型中没有考虑“受灾点-救援点-安置点”3 点协同运输方式，并且也没有考虑救援物资的运输情况。针对以上问题，本文作了如下改进。

本文模型是在研究受灾人员疏散方式的基础上得出最佳临时安置点的选址，即从预定临时安置点方案中选中最佳安置点。所以模型自变量为取值0～1 的变量x。运输工具的运输次数、运输距离、运输时间、运输的人员和物资为因变量。

基于上述问题描述，本文所建立的模型如下：

式（1）为系统目标，即最小化未转移的受灾人员和未满足的受灾点物资需求，可以看出式（1）是一个双目标问题。因为救援物资不充足会导致救援不力，所以假设在受灾情况下，救援物资运输和受灾人员转移具有同样重要的意义，这里引入惩罚因子q（人/kg），将救灾物资与受灾人员转化为同一目标类型。

式（2）表示约束总成本要在预算之内，总成本包括运输人员与物资的运输成本、救援物资的采购成本、安置点的建设成本等。

式（3）和式（4）分别表示已满足的物资需求加上未满足的物资需求等于受灾点总需求，已转移的受灾人数加上未转移的受灾人数等于受灾点受灾总人数。

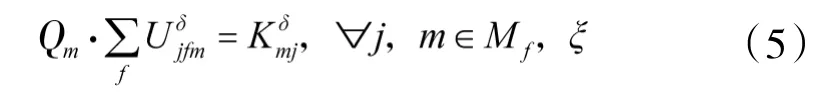
式（5）表示运输工具单次物资容量乘上运输次数等于已满足物资需求量。

式（6）表示运输工具单次人员容量乘上运输次数等于已转移的受灾人员数。

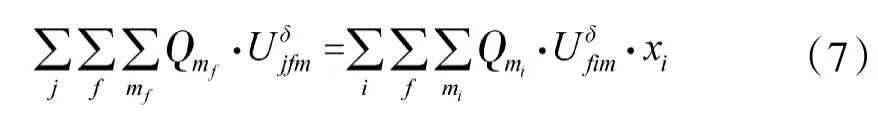
式（7）表示受灾点转移到救援点的人员等于救援点运输到安置点的人员。

式（8）表示转移到安置点i 的人员数不能超过安置点i 的人员容量，式（9）表示从安置点i 运输出去的救援物资不能大于安置点i 的救援物资的总量。

式（10）表示通过安置点、救援点、受灾点间的距离和运输工具行驶速度得出单次运输时间。

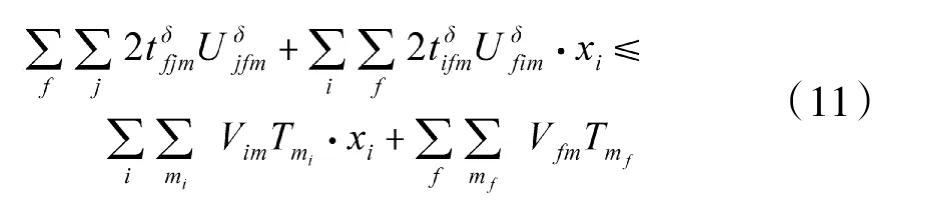
式（11）表示承担运输任务的运输工具的工作时长不能超过运输工具的有效时长。

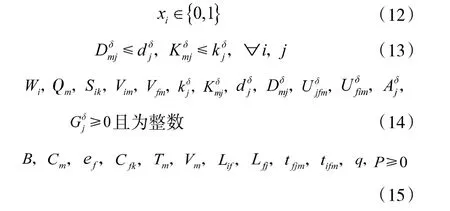
式（12）～式（15）是变量约束。

2 疏散模型算法设计

2.1 场景分解和最优值下界的确定

考虑到模型P1 中决策变量x与情景无关，且x为取值0～1 的变量，则将x分别转化为x，并加上相关非期望约束。即，用x来替换P1 中的x，定义非期望约束如下：

将式（16）代入到P1，获得模型P2。

假设1 模型P1 和模型P2 等价。

证毕。

从模型P2 的结构来看，除期望约束外，可以把其他的约束条件及目标函数按场景分解。因此，考虑松弛这个约束，并基于拉格朗日松弛把它加入到目标函数，得到模型P3。

假设2 式（18）的最优目标值是问题P2 最优目标值的下界。

证明根据弱对偶理论可得到上述结论，其证明过程可参见文献［6］。

通过上面的迭代方式可以把拉格朗日对偶问题按情境分解为多个独立的子问题求解。

2.2 拉格朗日对偶问题的分支定界算法流程

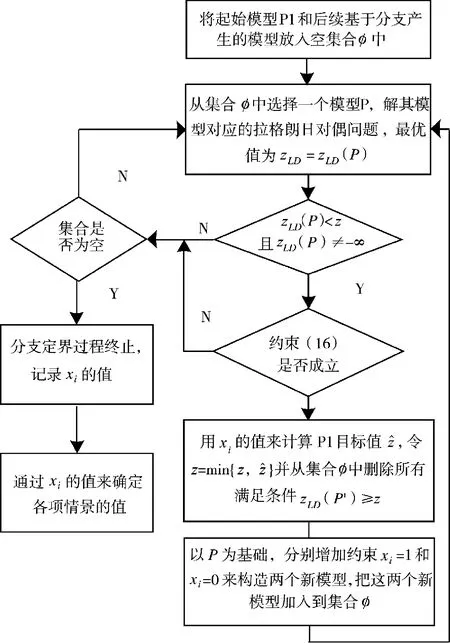
图1 算法流程图

3 实例研究

3.1 方案设计

设计一个简单的模拟场景来验证本文提出模型的有效性。数值计算是基于计算机软件进行，并通过C++来实现模型的分解和算法流程控制。

在模拟场景中，共有受灾点3 处，受灾点被洪水包围，在水域边缘设置救援点2 个，救援点里的救援人员会前往受灾点，将受灾人员通过水路运输工具运输到救援点。为使救援效率最大化，安置点的陆地运输工具之前会将救援物资运输到救援点，再将受灾人员转移回安置点。在安全地区设置安置点3 个。由于洪水的可预测性和不可避免性，在洪水爆发前，在安置点准备救援物资，采购救援物资的成本计算在预算范围之内。在一张洪水淹没范围图的基础上，设计了简化的固定设施布局图，如图2所示。

图2 固定设施布局示意图

其中，受灾点（圆圈标记）根据洪水灾情淹没范围情况确定，共计3 个。救援点（三角形标记）根据受灾点的分布和交通运输条件等因素选取，共计2个。安置点（四边形标记）根据人口容量，安全范围等条件进行选取，共计3 个。

3.2 参数设置情况

受灾点的情况，如下页表1 所示。

表1 受灾点情况

安置点的情况，如表2 所示。

表2 安置点的基本情况

安置点运输工具情况，如表3 所示。

表3 安置点运输工具基本情况

救援点运输工具情况，如表4 所示。

表4 救援点运输工具基本情况

表5 和表6 分别为受灾点与救援点的距离和救援点与安置点的距离。

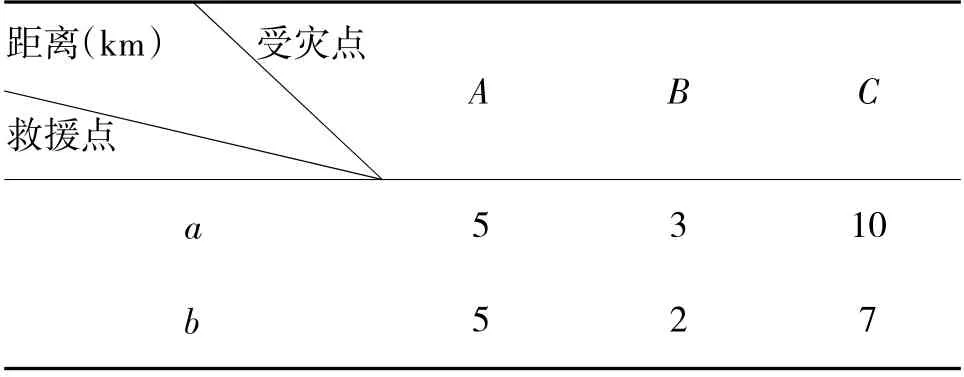
表5 受灾点与救援点的距离

表6 救援点与安置点的距离

最后未满足物资需求的惩罚因子设定为0.3。将预算设置为10 万元、20 万元、30 万元和40 万元4种情况。

3.3 结果分析

如表7 所示，在经费较低时，受固定设施成本影响，系统倾向于选择少量固定设施。随着预算的增加，安置点的人口容量限制了目标最小值，被选中的安置点量也增加。此外，先期被选中的安置点在经费增加的过程中一定会选中，这种现象也为应急选址决策带来启发。

表7 不同经费情况下的选址结果

表8 表示不同经费预算情况下，各种运输工具的运输次数和最小目标值。在自然灾害发生时，优先采用运输效率（单次运量/单次运输成本）大的运输工具。当最佳运输工具使用饱和后，会选择次优运输工具。就此例而言，所需的预算费用为30万元。

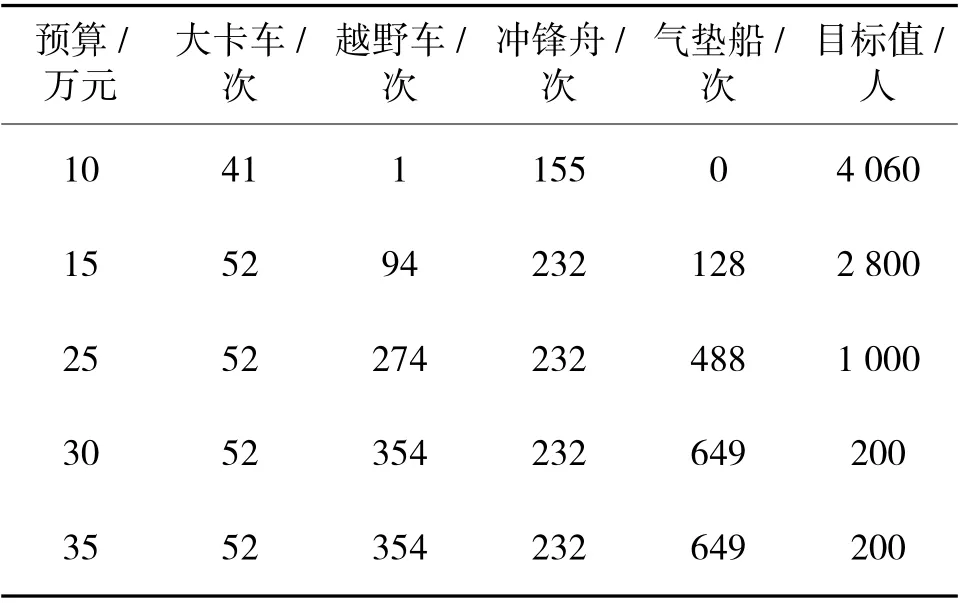
预算/万元目标值/人1041115504 060 1552942321282 800 25522742324881 000 3052354232649200 3552354232649200大卡车/次越野车/次冲锋舟/次气垫船/次

在现实情况中，可以通过这种方式得到一个大致的预算情况，并且通过计算运输工具效率，选择效率最高的运输工具。本文所建模型，能够帮助发现应急救援时的薄弱环节，如预算、运输工具效率、固定设施数量和容量等。

4 结论

本文针对重大突发事件情况，提出了“发生点-救援点-安置点”人员转移模型，并研究了基于多种场景情况下的转移模型分析算法。但研究过程中进行了一些简化假设，比如运输过程仅仅是以最短距离进行计算，没有考虑道路堵塞等情况。在人员疏散中，没有考虑人员的心理因素对人群行为造成的影响。后面的研究会考虑将这些简化因素一一加入到理论模型中，寻找突发事件中人员疏散的最优决策方法。