一种基于经验模态分解的弹道群目标关联算法

张怀念，周 焰，梁复台，张 晨

（1.空军预警学院，武汉 430000；2.火箭军指挥学院，武汉 430000；3.国防科技大学国防信息学院，武汉 430000）

0 引言

弹道导弹具有射程远、精度高、速度快和威力大等突出特点，是现代乃至未来军事斗争中战略威慑和战术应用的重要武器装备。为提升弹道导弹的突防能力，常常会采用集火攻击，多枚导弹在短时间间隔内密集发射，同时，运行到中段的弹道导弹还会释放大量的诱饵和假目标，由于在大气层外，这些诱饵和假目标的运动方向、速度与真弹头一样，而且相互之间的距离比较近。上述情况导致在跟踪目标过程中极易出现错误关联，导致混批、错批等问题发生，针对弹道群目标研究航迹关联问题迫在眉睫。

目前，航迹关联的算法主要分为统计方法和模糊数学方法。针对密集飞行的弹道目标群，当系统误差较大时，采用统计方法难以获得准确的统计误差，导致关联率显著较低；模糊数学方法虽然稳定性较好，但如何根据经验确定目标特征属性，以及构造隶属度函数则比较困难。针对弹道群目标航迹关联中的特征提取问题，进行了一些有益的研究。文献［9］从高距离分辨率雷达的一维距离像获得目标身份信息来辅助数据互联过程，在航迹交错之后重建航迹身份，但对传感器信源提出更多要求；文献［10］利用小波变换对目标特征值进行去噪，但目标特征量较为单一，降低了关联判断的可靠性。上述文献对航迹特征提取问题进行了一些努力，但针对弹道导弹这类具有显著特征的空间目标，没有从根本上给出系统性、普适性的解决方案。

作为一种近年来逐渐兴起的非线性信号处理方法，经验模态分解（EMD）得到了一些学者的广泛关注。基于EMD 的信号处理方法无需额外的先验知识，仅通过对数据本身的信息进行合理的函数分解，就能够较为准确地反映出原信号的特征信息。在此理论基础上，本文提出一种基于EMD 的特征提取算法，用于解决弹道群目标航迹关联问题。该算法利用EMD 方法，从量测数据中提取弹道目标群的特征信息，采用灰度方法对特征量进行对比判定，以提高弹道群目标航迹关联的正确率。

1 状态方程与测量方程

建立弹道导弹运动状态方程与测量方程，仿真目标运动及传感器测量，通过卡尔曼滤波方法得到目标的运动状态估计，最终得到弹道导弹目标飞行自由段航迹。

1.1 状态方程

1.2 量测方程

弹道目标的量测方程在雷达站球坐标系下描述，目标的测量向量为：

其中，ρ、θ、ω 分别为极坐标体系下雷达的目标径向距离、方位角、俯仰角。

弹道目标的量测方程为传感器的观测方程，为：其测量矩阵为：

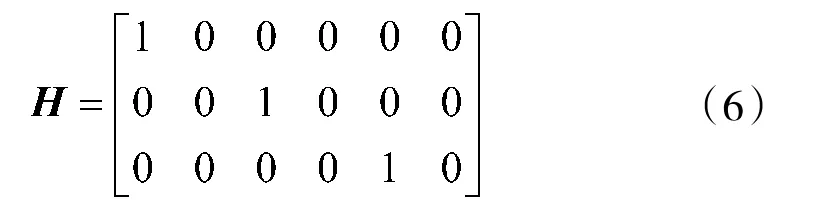
W（k）为具有协方差R（k）的零均值、白色高斯量测噪声。

量测噪声协方差矩阵

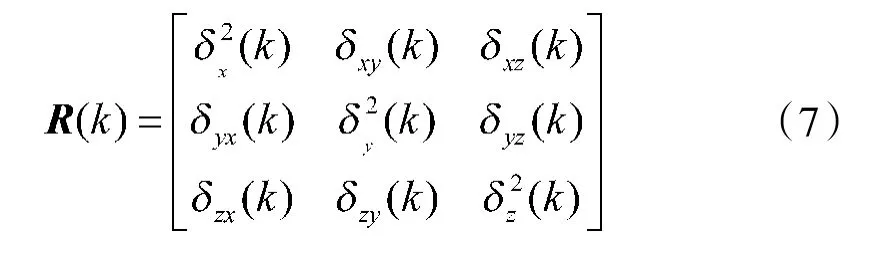
其中，δ（k）与目标在k 时刻的径向距离、方位角、俯仰角，以及雷达的测距和测角误差的标准差有关。

噪声序列的协方差矩阵取：

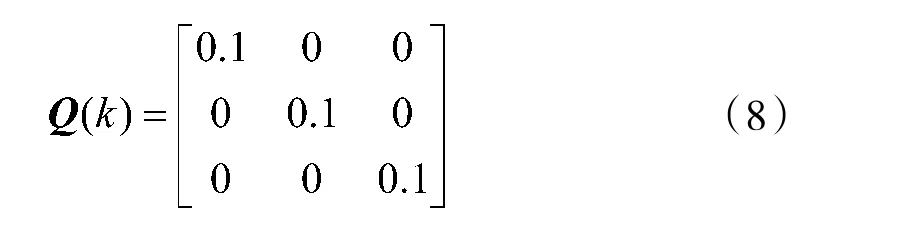
设传感器的测距误差、方位角误差、俯仰角误差分别为δ=200 m，δ=1°，δ=2°。

2 算法原理与实现

在进行弹道目标群航迹关联过程中，当传感器数量超过3 时，如果同时进行关联计算，则计算量会非常庞大，下文采用一种简单方式处理。对传感器1 得到的状态估计量和从传感器2 得到的状态估计量进行关联，对于关联成功的状态估计，进行数据融合处理后，再和传感器3 送出的状态估计量进行关联。依次类推，直至完成对所有传感器的关联融合计算。

2.1 基于EMD 方法的航迹特征提取

由Huang 等人于1998 年提出的EMD 方法，该方法能够根据时间序列的时间尺度自适应地确定数据特征，对非线性、非平稳的时间序列具有较好的降噪能力，广泛应用于经济、能源、气候等多个领域。本文将量测的航迹数据看作带有噪声的信号，利用EMD 方法将其分解为若干个本征函数（intrinsic mode function，IMF）和一个剩余分量，IMF 表征原始数据在不同时间尺度上的特征信息，剩余分量则表征了数据序列的趋势项。

利用EMD 方法对U和U分别进行分解可以得到相应航迹数据的IMF，虽然由IMF 组成的矩阵表示数据本身具有的特征，但无法对这些矩阵直接进行对比，因此，也难以判定对应的航迹是否关联。作为矩阵的固有特征之一，矩阵的奇异值具有较好的稳定性、比例不变性和旋转不变性，能有效地描述航迹数据对应的特征。因此，可按以下步骤获取各节点航迹特征：

2.2 灰关联度的计算

通过EMD 方法可以获得航迹数据的特征向量，因此，本节的关键问题是如何判定不同特征向量之间的相似性。如果将关联的特征向量看作先验模式，将被关联的特征向量看成待识别模式，那么航迹关联问题实际上是一个典型的模式识别问题。因此，可利用灰色分析技术研究航迹关联问题。特征向量相似性判定的核心是如何对向量关联度的计算，从而判定航迹间的相似性。设计如下步骤计算航迹特征向量间灰关联度：

2）采用区间值化的方法对特征向量进行标准化处理，以保证数据之间具有可比性：

3）计算第k 个指标的绝对差

特征向量中奇异值的大小对关联判决有着较大影响。通常，奇异值较大时，其权值可设置大一些；奇异值较小时，其权值可设置小一些。这样做的好处是可增大关键特征的辨识度。

则判决航迹e在t 时刻与航迹f关联，否则，判定局部节点1 的航迹e在t 时刻不与来自局部节点2 的任何一条航迹关联。其中，阈值可通过仿真确定，0.5≤ε＜1。

3 仿真结果与分析

为验证关联算法可行性，设计如下仿真环境：1）目标参数：弹道初始高度110 km，初始速度为4 000 m/s，射程约为820 km，采用三自由度动力学方程积分生成仿真弹道；2）传感器参数：采用扩展卡尔曼滤波（EKF）滤波器，距离量测标准差为1 000 m，方位角、俯仰角量测标准差均为0.002 rad。为检验算法性能，假设地基相控阵雷达部署在敌方弹道导弹发射点前方1 500 km 处，假设传感器已经进行了时空对准。相关正确率=正确判断次数/总判断次数。对仿真算例进行50 次蒙特卡洛仿真，计算平均关联率。

图1 为弹道群目标仿真场景。从图中可以看出，弹道目标群存在集火攻击和交叉现象，场景比较复杂。图2 为目标批次为10 时，不同采样次数下的全局关联正确率。从图中看出EMD 灰度算法显示出明显的优势，关联正确率随采样次数逐渐增大，最终保持在0.9 左右。而传统灰度算法约为0.85，加权法则不足0.8。本文算法相对于传统灰度算法正确关联率提高了6%左右，且收敛比较快。图3 为采样次数为30 时，不同目标批次下的全局关联正确率。从图中看出全局关联正确率随目标批次增加呈线性下降。相对其他两种算法，EMD 灰度算法基本稳定在0.9 左右，性能优势较为明显。

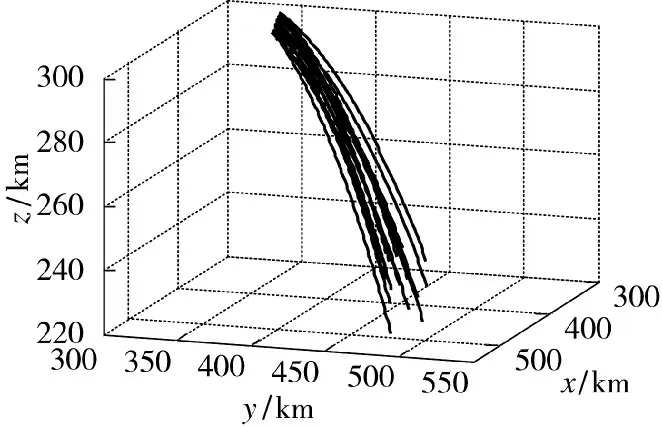
图1 弹道群目标仿真场景

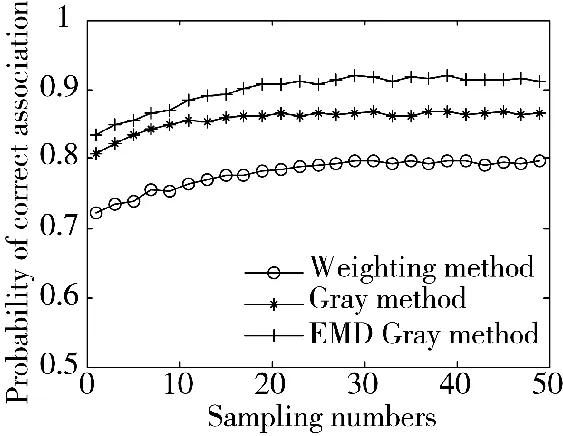
图2 不同采样次数下关联正确率

图3 不同批次目标下关联正确率

4 结论

本文针对集火攻击以及诱饵、干扰突防背景下的弹道群目标航迹关联中特征值难以提取的问题，提出基于EMD 提取特征值的灰度航迹关联算法。该方法直接利用EMD 分解提取航迹数据库的特征信息，由灰关联度判定特征向量间的相似性，从而确定航迹是否关联，避免了需要假设航迹数据服从典型分布的弊端。仿真结果表明，本文算法的性能明显优于传统灰度法和加权法，可为密集目标环境下弹道目标群航迹关联问题提供有效的解决方案。