高分辨雷达目标电磁散射特性复现方法

刘 颖，董兴佳，李 昂，何金叡

（解放军63861 部队，吉林 白城 137000）

0 引言

考核雷达对特定目标的识别、跟踪能力，最可靠的办法就是采用真实目标作为靶标来实测雷达性能。由于很多真实目标（例如敌方的飞机、舰船）难以获取，且按真实物理结构按1∶1 的比例进行仿制，其成本和周期也是难以承受的。因此，需要用替代办法来模拟真实雷达目标，通常采用金属物制作雷达靶标，以考核雷达导引武器的发现、跟踪、命中性能。目前制作雷达靶标时，将被模拟的真实目标视为点目标，只要求靶标的RCS（radar cross section，雷达散射截面）与真实目标RCS 的统计规律相同，可以称这样的靶标为点目标靶标。这种点目标靶标，不能反映真实目标的多散射中心所导致的角闪烁效应，难以满足高分辨率雷达的试验鉴定需求。

由于飞机和舰船等结构较为复杂，散射中心的存在多是离散的，从以往的散射中心计算理论也可以知道高频区的电磁散射主要是由局部的散射中心叠加作用而形成。散射中心模型可以精确描述雷达高分辨图像中呈现的特征，包括目标强散射源位置分布、散射类型和散射幅度起伏等，散射中心以往多是用于目标识别、目标姿态反演和目标隐身方面。沈明华等采用旋转不变算法计算散射中心，利用神经网络算法实现了对飞机目标的识别。孙清潭主要分析了目标姿态和散射中心极化比之间的关系，实现了快速反演目标姿态。上述研究从未涉及到考核我军雷达制导武器装备跟踪制导性能，本文拟解决的是一种高分辨雷达扩展目标散射中心的提取与复现问题，通过建立二维散射中心模型，计算散射中心特征参数，设计用于复现各散射中心的散射体的方法，为雷达制导武器靶标建设提供理论支撑和技术支持。

1 雷达扩展目标二维散射中心模型建立

1.1 模型建立

雷达与目标坐标系如图1 所示，频率为f 的电磁波以角度φ 对目标进行照射。根据光学区目标散射的特性，可以由各个散射中心的矢量叠加来等效目标总的响应E（f，φ），即：

图1 雷达与目标的空间关系

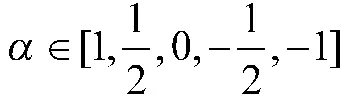
表1 参数α 对应的散射中心类型

二维目标后向散射场频率响应如式（2）：

求解P和P后，由式（3）、式（4）可以计算目标的各散射中心参数：

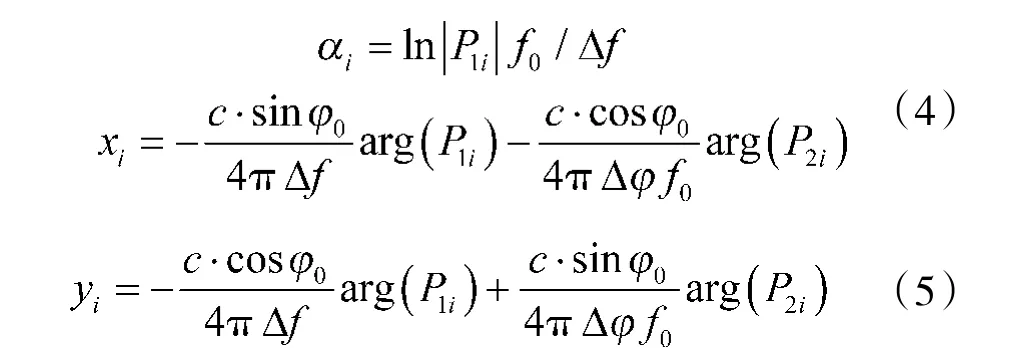
1.2 散射中心参数提取

1.2.1 散射中心个数参数估计

首先计算散射中心数目，采用盖氏圆盘方法，对于待求解的p×p 维矩阵R，r为第i 行第j 列的一个元素，令

O为第i 个盖氏圆盘，它的点在复平面上的集合表示为：

r为圆盘中心，r为圆盘半径，R 的特征值在O并区间。

为解决估计过程中可能出现的信号和噪声的盖氏圆相重叠的问题，将矩阵R 进行酉变换，首先将R 进行变换

1.2.2 散射中心类型、空间位置、幅度参数估计

用矩阵束算法提取散射中心的空间位置坐标、类型参量及散射强度参数。实现流程如下：

采用MEMP（矩阵束）方法建立Hankel 矩阵：

数据矩阵X可以表示为：

其中，P为Φ的主对角线元素。

与上述同理，求解P，P和P配对处理，代入式（4）、式（5）即可计算出相应的散射中心参数。

利用计算出的散射中心位置及类型参数，采用最小二乘法估计散射强度。

构造数据矩阵：

1.3 原始缩比模型标记及结构尺寸计算

通过将提取出的散射中心在空间映射到原始的缩比模型，明确原始目标结构上的散射中心源位置，在这个映射过程中，需要结合原始结构作进一步判断。本文采用的方法是：先在xy 平面上标记出散射中心位置，然后做沿z 方法的垂线与目标结构相关。如果相交区域为非连续且具有散射中心特征的结构，可视为其三维散射中心的位置。

用简单目标的组合体去等效重构原目标，因为简单目标的散射中心参数和几何结构尺寸之间的关系是确定并且量化的。表2 为不同几何结构对应的散射体设计准则。首先对非合作目标进行电磁仿真以获取其散射场数据，然后提取散射中心，通过散射中心参数与典型几何结构尺寸之间的定量关系，获取散射中心对应的几何结构，最后将这些结构组合起来，实现对靶标的等效重构。

表2 散射体设计准则

2 某飞机缩比模型靶标制作

对比某模型制作模拟靶标。真实模型几何参数为：翼展41.40 m，机长36.88 m，机高11.16 m。缩小比例尺度为25，缩比后的模型大小为1.65 m×1.47 m×0.45 m，其模型结构如下页图2 所示。

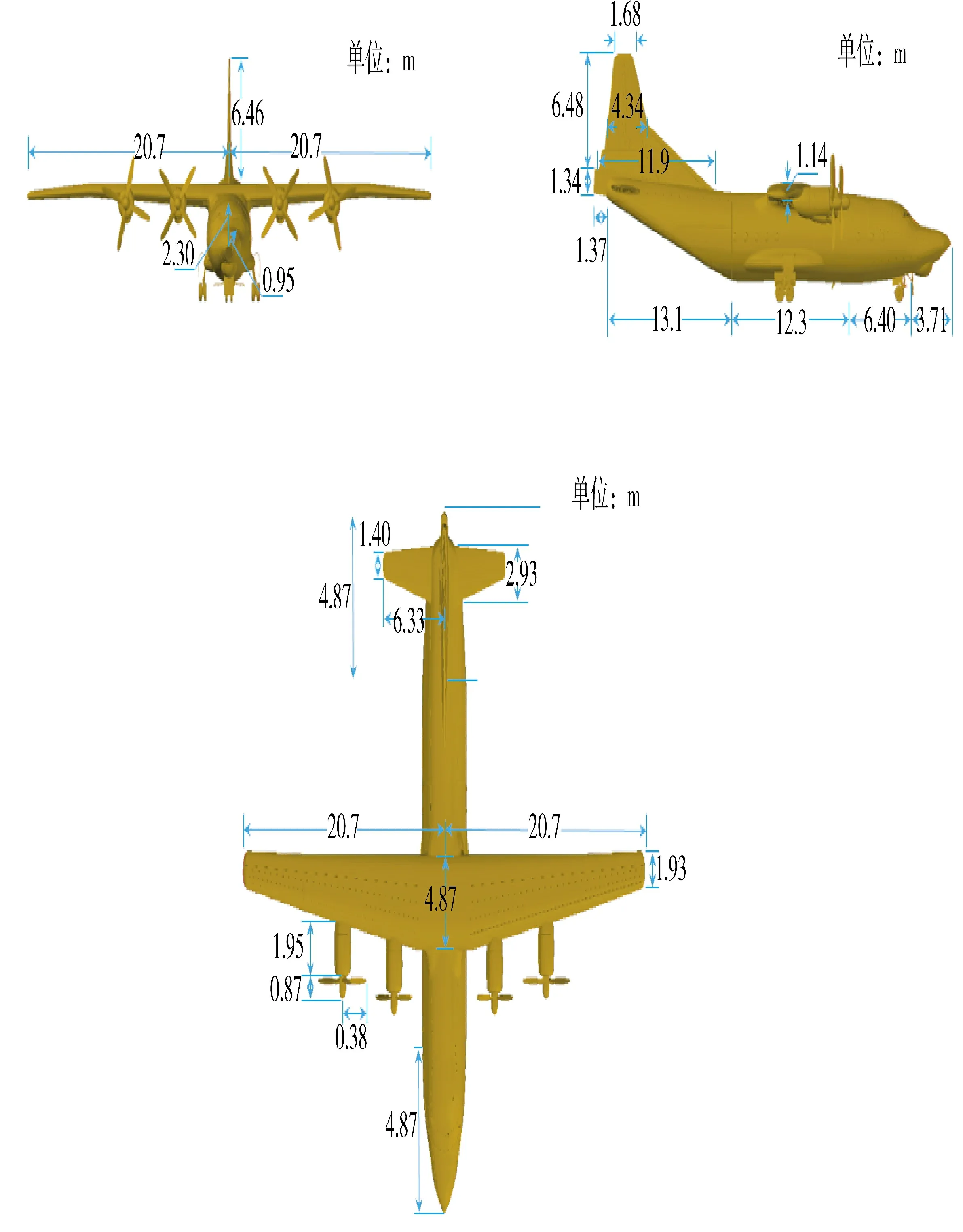
图2 某模型结构尺寸

2.1 散射中心提取和散射体尺寸解算

通过在一定的小角度范围内，本案例选择-10°～10°范围，且在频率范围9.0 GHz～10.0 GHz，频率间隔为80 MHz，获取目标的回波信号。可以通过盖氏圆盘理论，获取散射中心的个数为23。通过矩阵束算法和最小二乘法可以得到真实模型的散射中心，然后作映射回原始模型，结果如图3 所示，获取的散射中心对应的散射体相关数据如表3 所示。

表3 散射中心对应基本散射体相关数据

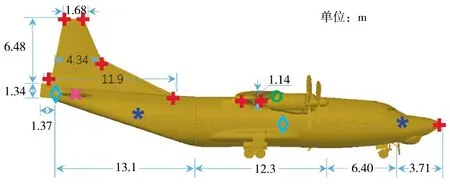
图3 真实模型的散射中心映射关系

2.2 简化基本结构至基本几何体

根据原始缩比模型，标注出相应的缩比模型上强散射中心的位置，通过保留强散射中心结构，平滑与简化其余的结构，可以得到等效模型靶标结构尺寸图，最后整体的尺寸为1.52 m×1.28 m×0.44 m，具体结构如图4 所示。

图4 几何体组等效简化模型

综合考虑靶标的尺寸、重量与成本等因素，采用木制主体结构加强反射金属锡纸表面的方式，加工得到简化模型的实体靶标，实物图如下页图5 所示。

图5 等效靶标模型实物图及暗室

原始模型RCS 和设计制作的模拟靶标RCS 随雷达入射角-180°～180°范围内变化如第132 页图6所示，对比结果如图7 所示，可以看到本方法的复现方案在全向具有较好的符合程度。

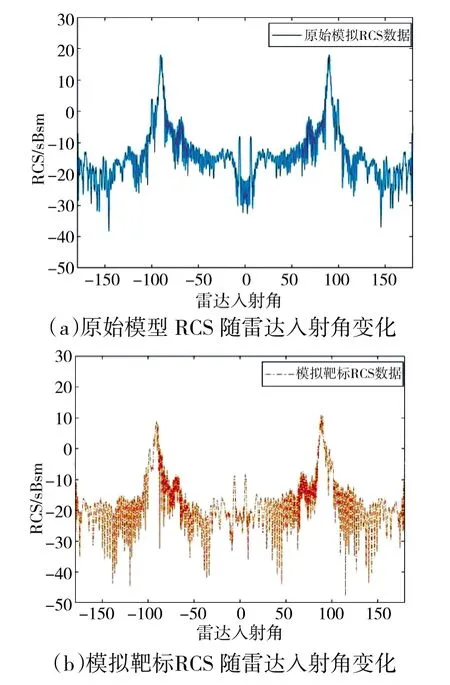
图6 RCS 随雷达入射角变化情况

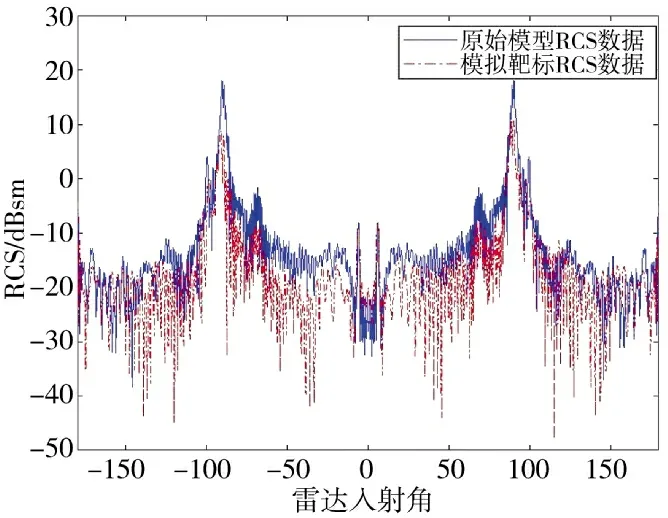
图7 等效靶标测试RCS 结果与原模型结构仿真分析全向结果对比

3 结论

针对如何构建雷达扩展目标模拟靶标展开研究，基于散射中心理论构建等效物理模型，实现了基于盖氏理论提取散射源中心数，矩阵束算法、最小二乘法提取散射中心相关参数，设计了模拟靶标复现方案。采用某模型为实例，对其进行仿真，提取二维GTD 散射中心，设计等效模型靶标，并进行加工与暗室测试，验证了复现方案的正确性，为雷达制导武器靶标建设提供理论支撑和技术支持。