某7.62 mm 电击发狙击枪内弹道多目标优化设计*
2022-09-14蔡昌鹏薛百文张哲伟
蔡昌鹏,薛百文,杨 臻,张哲伟
(中北大学机电工程学院,太原 030051)
0 引言
21 世纪以来,随着军事科学技术的发展,狙击步枪作为一种可以远距离精准射击的武器,在现代战争中的作用越来越大,同时也对其提出了更高的要求。当前国内狙击枪的射击精度可以保证在1MOA,想要更高的射击精度,需要对初速极差与内弹道全过程时间极差进行更精准的控制。
对内弹道全过程时间极差进行控制是一种新的构想,相关研究较少,现有的研究都是不同参数对底火发火时间精度的影响分析。韩体飞等研究了击发药质量和电阻丝均匀性对发火时间精度的影响,通过优选可以使电阻丝成为可忽略因素,并且找到了发火时间精度最大时击发药的质量;姚则武等研究了激发电源和发火电流以及击发药参数对发火时间的影响,结果表明,当电流强度处于临界状态时,对电底火作用时间影响最为明显,击发药量直接影响能量输出,对发射药作用时间影响最为直接;金建峰等研究了不同低温应力加载方式下发火时间的变化。
我国对弹丸初速极差的研究较多,在对弹丸初速的影响因素分析方面开展了很多工作。闵建平等建立发射药能量特性与初速极差量之间的数学模型,通过分析发射药物理化学特性,以确定初速极差量;彭志国等就身管热散失这一因素对弹丸初速的影响作了定量分析,建立了身管热散失的数学模型,并进行了数值计算;苏红星等建立了弹丸初速的影响因素计算模型,计算分析了气体炮中气室容积、气室初始压力、发射管长度3 个影响因素对气体炮弹丸初速的影响;张亮亮等通过FLUENT 计算平台,获得了膛底压力和弹丸初速的分布,进而对电热化学炮的出口速度进行优化控制。
通过对某7.62 mm 电击发狙击枪内弹道优化设计,提升弹道一致性,进而提升射击精度,并为其他型号狙击枪设计人员提升射击精度提供了参考。
1 基于电底火的内弹道计算模型
采用经典内弹道模型,在经典内弹道的基础上,考虑基于电底火的内弹道全过程的时间,即从电热桥丝通电到弹底出枪口的时间。
电阻升温时间t为:

式中,I 为电流;c 为电热桥丝材料的比热;r 为电热桥丝材料的密度;ρ 为电热桥丝材料的电阻率;d 为电热桥丝的直径;T 为击发药发火温度。
密闭爆发器中点火压力与点火时间的关系,如表1 所示。

表1 密闭爆发容器中点火压力和点火时间的关系
通过MATLAB 非线性拟合,得到点燃发射药时间t:

式中,m、f、α分别为击发药用量、火药力及余容;m、Δ 分别为发射药的装药量及密度;V为密闭爆发器容积。
则内弹道全过程时间t 为:

式中,t为开始通电至电阻升温到击发药发火温度的时间;t为击发药发火至点火压力达到传统机械击发强度的时间;t为通过经典内弹道模型计算而得的弹丸膛内行程时间。
基于电底火的内弹道相关参数如表2 所示。

表2 内弹道相关参数
运用数值计算软件MATLAB 进行解算,得到内弹道时间与行程的关系,结果如下页图1~图2 所示。
由图1 可知,弹底出膛口的速度为782.5 m/s,由图2 可知,从开始通电到弹底出膛口的时间持续了1.949 ms。根据相关试验数据,优化前某电击发狙击枪的速度极差为15 m/s,时间极差为0.53 ms。本文拟通过对基于电底火的内弹道参数的优化,将速度极差控制在10 m/s 以内,将时间极差控制在0.5 ms以内。

图1 速度-时间图
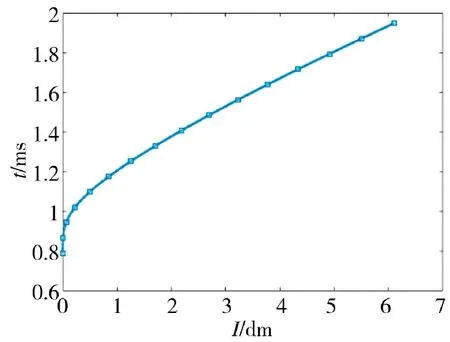
图2 时间-行程图
2 参数误差范围优化及灵敏度分析
2.1 灵敏度分析理论
灵敏度分析方法即分析一个系统响应或输出对系统输入、系统相关参量变化敏感程度的方法。通过灵敏度分析的方法,可以找到设计变量中对目标函数影响较大的变量,从而得到设计最优解。本文将使用ISIGHT 分析软件中的DOE 模块,分析基于电底火的内弹道相关参数对弹丸内弹道时间矢量和出膛口速度矢量的影响规律和影响程度,对时间和速度进行灵敏度分析选用的是最优拉丁超立方试验设计方法。
2.2 DOE 试验计划
1)响应
将内弹道时间和弹丸出膛口速度作为灵敏度分析的目标函数,确定各参数对时间和速度的影响程度。
2)因子
内弹道时间计算模型参数涵盖了电底火参数、身管内膛参数、弹药参数、火药性能参数、弹丸结构参数等,综合火力系统的具体情况,本文选取以下参数作为分析参数:
电底火参数:发火电流I、电热桥丝直径d;
身管内膛参数:枪膛横断面积S、弹丸行程长l、药室容积W;
弹药参数:弹丸质量m、发射药装药量m、发射药的装填密度Δ、击发药量m、发射药药弧厚e。
3)约束条件的设置
根据设计要求,约束条件设置如下:
777.5 m/s≤v≤787.5 m/s
1.699 ms≤t≤2.199 ms
4)水平
本文将只影响时间的参数范围设为±10%,将其他参数范围设为±5%。
5)DOE 的执行
多学科优化软件中集成计算内弹道的MATLAB 软件并运行试验设计(DOE)的方法如图3 所示。在DOE 组件中,设置试验设计方法为最优拉丁超立方法,同时定义设计变量以及变量的变化范围,并根据需要指定目标函数。

图3 ISIGHT 试验设计模型
2.3 参数误差范围优化
依据上述水平的参数随机进行200 次计算,得到的时间和速度结果如图4、图5 所示。发现时间的极差虽然不符合精度要求,但跳动范围较小,速度的跳动范围偏大,需要对上述参数的变化范围进行优化。

图4 时间的计算结果分布图
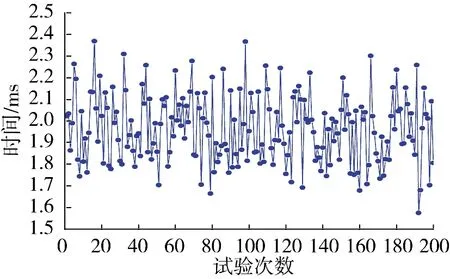
图5 速度的计算结果分布图
根据实际要求,结合MATLAB 计算程序,本文以速度的标准值782.5 m/s 为优化目标,对只影响时间以外的参数的误差范围进行调整,通过最优拉丁矩阵试验设计方法产生样本点;每组参数都进行200 次试验,参数误差范围调整至±0.5%的时候满足极差的点已经达到95.5%,再对参数范围进行微调;调至±0.4%时,如图6~图7 所示,200 次试验的速度满足极差777.5 m/s≤v≤787.5 m/s,时间还未完全落在约束范围内,以上通过调整误差范围得到的计算结果在约束范围内的分布概率如图8 所示。可以看到,速度的计算结果随着范围的减小,最终分布概率达到100%,时间的计算结果的分布概率虽然变化不明显,但也从92%提升到95%。

图6 范围调整至±0.4%速度计算结果分布图

图7 范围调整至±0.4%时间计算结果分布图
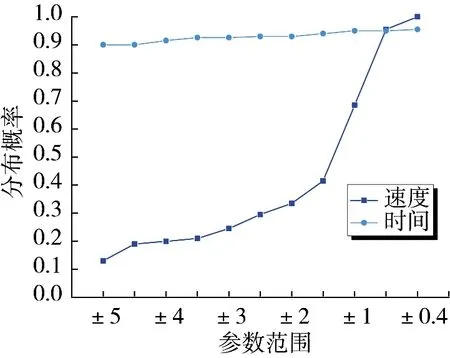
图8 计算结果的分布概率
以时间的标准值1.949 ms 为优化目标,保持优化后的其他参数误差范围不变,对发火电流、电热桥丝直径和击发药药量误差范围按比例进行调整,同样通过最优拉丁矩阵试验设计方法产生样本点,每组参数都进行200 次试验,如图9 所示,当参数误差缩小至±6%时,200 次试验的极差同时满足了时间精度和速度精度。

图9 误差调整至±6%时计算结果分布图
因此,根据计算结果,将发火电流、电热桥丝直径、击发药量的变动范围设置为±6%,其他参数的变动范围均设置为±0.4%。
2.4 灵敏度分析
本文根据最优拉丁超立方试验设计的分析结果,用Pareto 图反映设计变量参数对目标函数贡献百分比,即反映枪管结构及弹药参数对内弹道时间和弹丸出膛口速度的影响程度。枪管结构及弹药参数对内弹道全过程时间和出膛口速度的Pareto 图如图10~图11 所示,横轴反映了各参数的影响百分比,纵轴表示各个参数。

图10 各参数对时间的Pareto 图
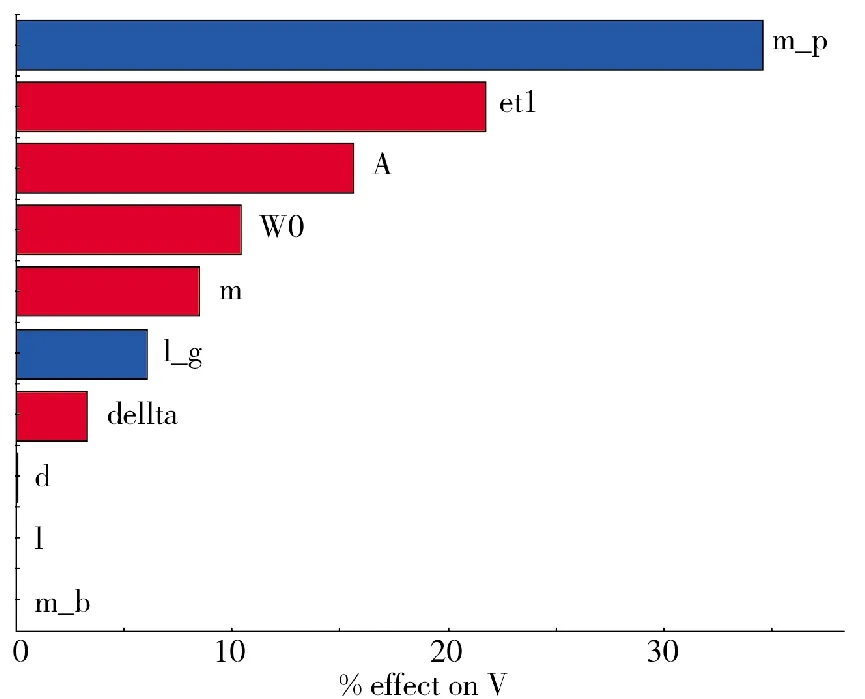
图11 各参数对速度的Pareto 图
由图10 可知,电热桥丝直径对时间的影响占比最高,约为58%,电流对时间的影响次之,占30%左右;由图11 可知,发射药装药量、发射药弧厚和枪膛横断面面积对速度的影响占比都比较大,分别约为35%、22.5%和17%,电热桥丝直径、电流、击发药量对速度几乎没有影响。图中蓝色部分代表正相关,红色部分代表负相关,由图10 可知,时间随电热桥丝、药室容积等的增大而增大,随电流、发射药量和击发药量的增大而减小;由图11 可知,弹丸初速度随发射药量和弹丸行程的增大而增大,随其他参数的增大而减小。
综上所述,击发药量和发射药密度对时间和速度的影响程度都较小,所以本文选择其余8 个参数进行优化。
3 内弹道多目标优化设计
上一章对参数的范围进行了控制,将时间和速度控制在约束条件以内,本章通过优化在参数范围内寻求一组最优解,以达到约束范围内时间最小且速度最大的目的。
3.1 优化模型的建立
3.1.1 设计变量的确定
前文通过最优拉丁超立方试验设计方法对各参数进行灵敏度分析,根据灵敏度分析的结果,除击发药装药量和发射药密度影响较小,其余参数都有不同程度的影响,本文将这8 个参数作为优化设计变量,具体参数取值范围如表3 所示。

表3 各参数设计变量取值范围
3.1.2 优化数学模型建立
取8 个枪管结构参数作为优化设计变量,同时,以时间达到最小值,速度达到最大值为优化目标,对应的优化数学模型如下:

其中,F(x)为弹丸起始扰动目标函数;x为结构参数设计变量,共8 个;x、x分别为设计变量的取值下限和取值上限。
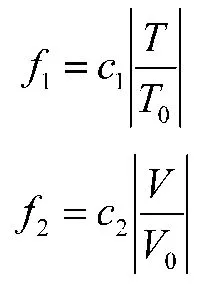
式中,f为时间目标函数;f为速度目标函数;T、P为弹丸相应参数的初始值;c、c为根据各弹丸参量的影响程度来确定的经验值,且c+c=1。
3.1.3 多目标算法参数设置
1)AMGA 算法参数设置
设置AMGA 算法的种群大小的为40、迭代次数为40 次,函数求值次数为1 000,档案大小为500,Pareto 大小为100,交叉概率为0.9,变异概率为0.5,交叉分布指数为10,突变分布指数为20。
2)NSGA-Ⅱ算法参数设置
设置NSGA-Ⅱ算法的种群大小为20、遗传代数为50 代,设置交叉概率为0.9,变异概率为0.02,然后进行优化计算。
3)MIGA 算法参数设置
设置MIGA 算法的子种群规模为10,岛的个数为10,总群体规模数为子种群规模与岛数的乘积即为100。设置总共进化的代数为200 代,交叉概率设置为0.9,变异概率为0.08,迁移概率为0.2,迁移的间隔代数为5,保留到下一代的精英个体数量设置为1。
3.2 优化结果及分析
在对内弹道参数进行灵敏度分析的基础上,利用AMGA、NSGA-II、MIGA 以范围内最小时间和最大速度为目标对各参数进行优化计算。按上节中的参数设置进行基于电点火的内弹道优化,得到8 个目标量的优化结果,如下页表4 所示。
由表4 可知,经过1 000 次迭代后,3 种算法标定的参数大致相同,发射药装药量和药室容积这2个参数通过算法优化的取值大致相同,但是,3 种算法对电热桥丝直径和发火电流的优化值明显有别于初始参数。各参数优化取值与上节灵敏度的计算结果的影响规律基本一致,即采用近似模型进行寻优计算,在提高计算效率的同时又能够充分保证其计算精度。通过3 种算法优化后的结果下页图12、图13 所示。
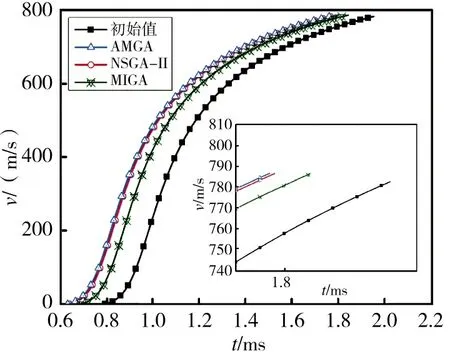
图12 优化前后速度-时间对比

图13 优化前后时间-行程对比
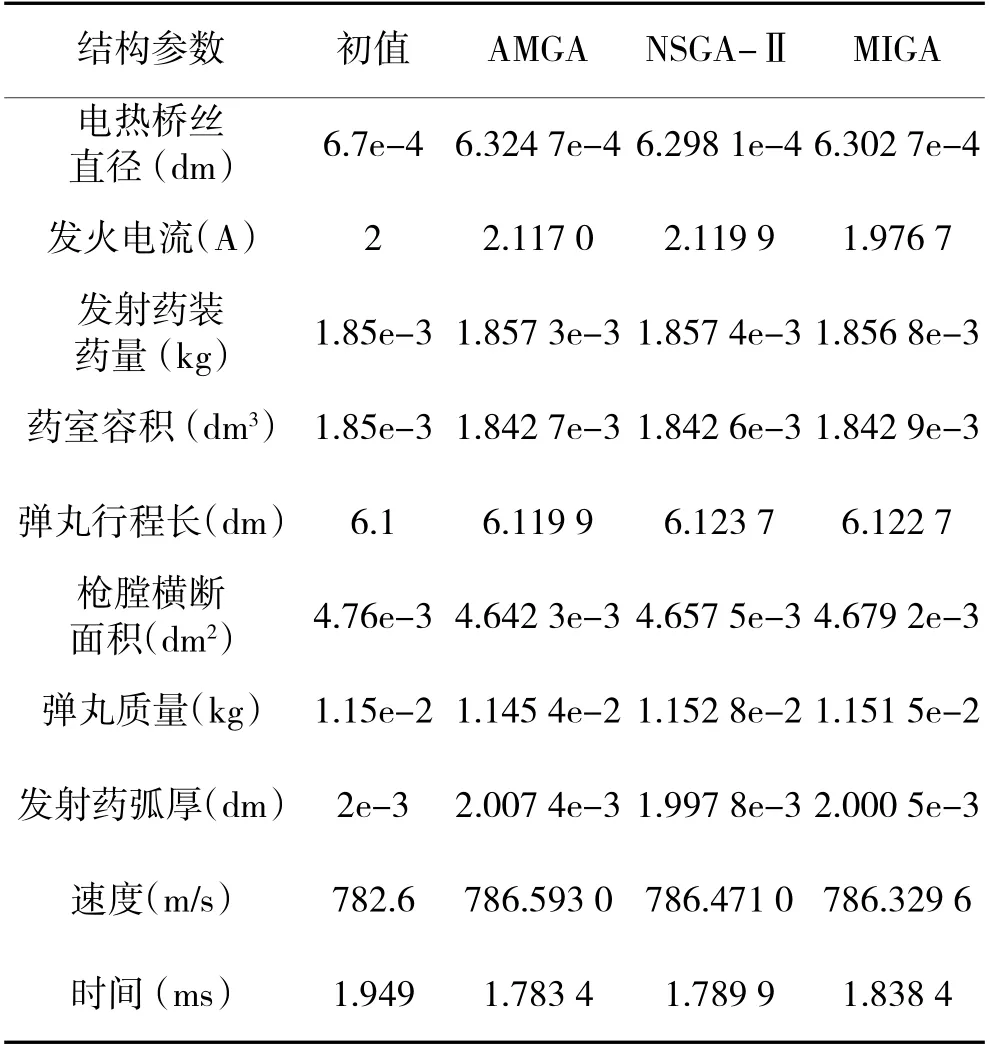
表4 各参数优化前后值对比
3 种算法的对比分析如下:
1)对比3 种多目标算法的仿真时间,AMGA 算法优化时间最短,符合其算法收敛速度快的特点;而NSGA-Ⅱ和MIGA 算法在优化变量较少的情况下,优化所用时间在接受范围内。
2)对比3 种多目标算法的计算结果,仅从选出的具有代表性的3 组数据可以看出,对于多目标优化,MIGA 算法没有得到比较满意的结果;而AMGA 较另外两种算法寻优能力强,得到的结果符合要求。
3)从优化前后对比图可以看出,相对于另两种算法,AMGA 算法得到的优化结果具有最小的时间为1.783 4 ms。虽然NSGA-Ⅱ算法与AMGA 算法的时间大致相同,但其计算得到的速度略低。同样,MIGA 算法优化得到的速度较为理想,但是时间没有明显的降低。
因此,本文选择AMGA 算法优化后的结果作为最优结果。
4 试验验证
试验现场布局如图14 所示,试验采用光电靶测试弹丸初速,采用晶体管测时仪测试枪弹从通电到弹底出枪口的时间,试验射击优化后高精度电击发狙击弹40 发。

图14 试验现场图
试验结果如表5 所示,试验表明,弹丸初速试验平均值与内弹道计算结果偏差为0.84%,内弹道全过程时间试验平均值与内弹道计算结果偏差为6.54%,初速极差试验值相比优化前提高了40%,内弹道全过程时间极差试验值相比优化前提高了5.6%。

表5 试验结果数据
5 结论
1)本文构建了基于电底火的内弹道计算模型,并将点燃击发药时间与点燃发射药时间考虑进内弹道时间内,提出了内弹道全过程时间的计算方法。
2)通过最优拉丁超立方试验设计方法,以时间极差范围和速度极差范围为目标函数来优化系统参数的误差范围,当枪膛横断面积、身管长度、药室容积、弹丸质量、发射药量、发射药装填密度和药弧厚的误差范围优化至±0.4%,击发药量、发火电流和电热桥丝直径的变动误差范围优化至±6%时,内弹道全过程时间极差和初速极差都能满足要求。
3)通过灵敏度分析优化范围后各参数对时间和速度的影响程度,选取影响较大的几个参数为后续优化的设计变量,选用AMGA、NSGA-Ⅱ、MIGA 3 种多目标优化算法进行优化,得到在满足条件下的枪弹参数最优解。
4)经过试验验证,内弹道数值计算结果较为理想,目标函数、优化设计变量选择合理,优化后的初速极差与时间极差的试验值达到了预期目标,具备更好的弹道一致性。
