考虑老年人感知满意度的社区居家养老护理人员调度策略研究

任宗伟, 刘钰冰

(哈尔滨商业大学 管理学院,黑龙江 哈尔滨 150028)

0 引言

护理人员调度作为社区居家养老模式下服务输送的重要环节，直接影响其服务效率与运营成本。因此，对护理人员进行合理的调度具有重要的研究意义。

目前，学者们从不同的角度展开研究。袁彪等考虑多类型护理人员，建立了混合整数规划模型[1]；陶杨懿等考虑服务时间窗、服务需求等约束，建立了数学模型[2]；吴萌等考虑服务周期，提出了面向随机性周期重复需求的调度模型[3]；袁彪等又考虑随机服务时间和最迟开始服务时间，建立了带补偿的随机规划模型[4]。以上研究的目标均从运营成本的角度考虑，对于如何提高满意度的研究有待深入。

并且现有的大多数研究都离不开车辆路径优化问题，例如Allaoua等将人员安排和路径规划有效结合起来，处理家庭护理问题[5]；Mankowska等考虑了个人服务要求和服务需求的相互依赖性，建立了家庭医疗护理路径和调度模型[6]，这为本文建立模型提供了强有力的支持。关于模型的求解，学者们设计了自适应大规模邻域搜索算法[2]、改善的蚁群算法[7]等求解方法。

另外，老年人是服务需求的主体，需要考虑老年人感知满意度。近年来，学者们对人的行为感知进行了大量研究。王旭平等提出应急物资调度决策应注意考虑公众的心理因素[8]；姜洋等考虑了多个行为主体并提出了单机调度干扰管理模型[9]；刘桔等构建了面向师生感知满意度的双边匹配决策模型[10]；李怀明等构建了考虑双方灾民感知满意度的模型[11]。上述研究为本文建立感知满意度函数提供了借鉴。

基于此，本文以社区居家养老预约服务为背景，融合前景理论和模糊理论从等待时间、护理人员偏好和服务价格偏好三个方面建立感知满意度函数，构建主要目标为最大化老年人综合感知满意度，次要目标为最小化社区居家养老服务中心运营成本的优化调度模型，以期为护理人员调度提供决策支持。

1 问题描述

社区居家养老服务中心能够提前获得服务类型、行为偏好等信息，根据老年人服务需求订单构建社区居家养老预约服务调度模型，如图1所示。

2 老年人综合感知满意度函数

通过问卷调查分析得出等待时间、护理人员偏好、服务价格偏好是老年人感知满意度最重要的影响因素。因此，本文从以上三个方面建立老年人感知满意度函数。

2.1 等待时间感知满意度函数

2.1.1 等待时间感知满意度的衡量

如图2，运用前景理论来刻画等待时间感知满意度函数，采用模糊理论对时间进行模糊化处理，从而建立老年人等待时间感知满意度函数[12]。

2.1.2 建立等待时间感知满意度函数

(1)

2.2 护理人员偏好感知满意度函数

2.2.1 老年人行为偏好的衡量

将老年人对护理人员的熟悉程度划分为5个等级，用集合{0，0.25，0.5，0.75，1}表示，分别对应{很不熟悉，不太熟悉，中等熟悉，比较熟悉，非常熟悉}，具体取值根据服务历史数据确定。依据熟悉程度矩阵可以得到老年人的偏好序列。运用前景理论的价值函数分别计算老年人对于每一位次护理人员的心理感知损失和收益[13]。

2.2.2 建立护理人员偏好感知满意度函数

为了便于建模及求解，高端护理人员序列依次为1、2、…、s；普通护理人员序列依次为s+1、s+2、…、s+p。σ表示在两类护理人员偏好序列的子序列内部，老年人心理感知偏差程度；τ表示在两类护理人员偏好序列的子序列之间，老年人心理感知偏差程度；τ>σ表示老年人更偏好高端护理人员；δjk表示在第j个老年人对护理人员的偏好序列中，第k个护理人员的位次；Ljk表示当第j个老年人的护理人员为第k个护理人员时，老年人的心理感知损失矩阵；Gjk表示当第j个老年人的护理人员为第k个护理人员时，老年人的心理感知收益矩阵。

选定δjk=1的护理人员为参考点，老年人的心理感知损失矩阵为:

(2)

(3)

选定δjk=s+p的护理人员为参考点，老年人的心理感知收益矩阵为:

(4)

(5)

护理人员偏好感知满意度为:

hj=Ljk+Gjk

(6)

对其进行归一化处理，得到：

(7)

2.3 服务价格偏好感知满意度函数

π表示当服务价格与老年人心理期望的服务价格不相匹配时，老年人心理感知的偏差程度；φjk表示在第j个老年人对服务价格的偏好序列中，第k个护理人员的位次；Qjk表示当第j个老年人的服务价格为第k个护理人员等级所匹配的服务价格时，老年人的心理感知损失矩阵；Ujk表示当第j个老年人的服务价格为第k个护理人员等级所匹配的服务价格时，老年人的心理感知收益矩阵。

选定φjk=s+p的护理人员等级所匹配的服务价格为参考点，老年人的心理感知损失矩阵为:

(8)

(9)

选定φjk=1的护理人员等级所匹配的服务价格为参考点，老年人的心理感知收益矩阵为:

(10)

(11)

服务价格偏好感知满意度为:

bj=Qjk+Ujk

(12)

对其进行归一化处理，得到:

(13)

3 数学模型

3.1 假设条件

(1)只有一个社区居家养老服务中心，且每个护理人员的起点和终点都在社区居家养老服务中心；

(2)一个护理人员一次只能为一个老年人服务；

(3)不考虑护理人员到达老年人位置的天气、交通等特殊情况发生；

(4)不同类型老年人服务需求的服务时间服从不同的正态分布；

(5)老年人对高端护理人员的偏好程度一定大于普通护理人员；

(6)老年人对服务价格低的偏好程度一定大于服务价格高；

(7)高端护理人员的服务价格高于普通护理人员。

3.2 符号说明

(1)参数设计

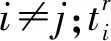
(2)决策变量

(14)

(15)

3.3 模型建立

(1)目标函数

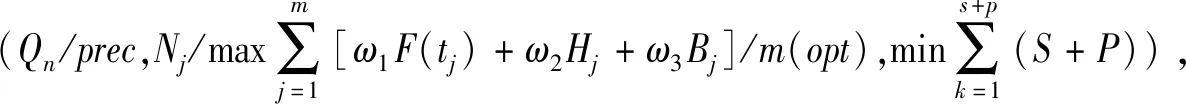
(16)

(17)

(2)约束条件

ω1+ω2+ω3=1,ω1,ω2,ω3∈[0,1]

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

tj=tkjμ,j∈[1,m];k∈[1,s+p]

(28)

模型中，式(16)为主要目标，式(17)为次要目标，式(18)～(28)为约束条件。其中：式(18)确保各满意度权重值的合理性；式(19)表示每个老年人只能被护理人员提供服务一次；式(20)～(22)表示每个护理人员从起点0出发，在为若干个老年人提供服务之后，回到起点；式(23)表示保证每个老年人都被提供服务且只由一个护理人员提供服务；式(24)～(25)表示如果老年人i、j在护理人员k的服务路线上，那么老年人i、j将由护理人员k提供服务；式(26)表示护理人员k到达老年人j位置的时间；式(27)表示护理人员k从老年人i到j的旅途时间，其中i≠j；式(28)表示老年人j的实际等待时间。

4 求解算法

模拟植物生长算法与传统优化算法相比，具备较好的稳定性、收敛性、精确度，在云作业调度[14]、集装箱码头调度[15]等领域均取得了研究成果。

4.1 植物向光性生长机制的数学描述

假设一棵树从根部X0处长出树干E，此时假设在树干E有l个比X0生长条件好的生长点记作XE1,XE2,…,XEl，对应各生长点的形态素浓度记作PE1,PE2,…,PEl，形态素浓度值为:

(29)

上述公式中：f(*)为所在点的环境信息函数(目标函数)。利用掷小球的方法产生[0,1]之间的一个随机数。

各生长点形态素浓度更新公式:

(30)

(31)

4.2 求解步骤

Step1确定初始可行解。根据普通和高端护理人员的数量确定根部生长点X0，求出对应的目标函数值f(X0)，并令Xmax=X0,fmax(Xmax)=f(X0)。护理人员调度方案利用10进制编码，若将2个护理人员调度给10个老年人，表1为其中的一种护理人员调度方案。

表1 调度方案示例

Step2用遗传算法求解以单个护理人员行程最短为目标的服务顺序。

Step3以X0为基础，按照随机两点交换方式产生200个新生长点。根据约束条件验证生长点的可行性。

Step4求出各个生长点的目标函数值，并与fmax(Xmax)进行比较，若大于fmax(Xmax)则置换Xmax和fmax(Xmax)。

Step5根据公式(30)和公式(31)计算各个生长点的形态素浓度。利用掷小球的方法选取下一生长点。

Step6重复上述步骤Step2～5，直到不再产生新的生长点或达到迭代次数。以上步骤的流程如图3所示。

为了实现老年人感知满意度及成本的均衡优化，引入公式η=1-(λ1×(1-Y)+λ2×(Z/(1.5s+p)))。称η为护理人员调度综合满意度。其中Y表示老年人综合感知满意度，Z表示安排上岗的护理人员标准数量，本文近似地设置为1个高端护理人员相当于1.5个普通护理人员。λ1和λ2表示权重且λ1+λ2=1。

5 仿真示例

5.1 仿真描述

本文通过调研哈尔滨市某一养老机构，获得某一天的数据构建测试算例仿真。参数如下：100个老年人、10个护理人员，高端和普通护理人员各为5人。模拟植物生长算法迭代次数设置为100次。采用欧式距离，时间以min进行换算。5种老年人服务需求的服务时间服从的正态分布分别为{(40,22);(20,12);(30,52);(15,22);(30,12)}；服务通知的时间延迟率服从[1.2,1.5]均匀分布；v=1；σ=2；τ=8；π=1；α=β=0.88,λ=2.25。

5.2 仿真分析

(1)等待时间感知满意度分析

最优调度方案如表2所示，老年人整体的平均等待时间感知满意度为0.883，如图4。此时，ω1=1；ω2=0；ω3=0;λ1=1;λ2=0;S=5,P=5。

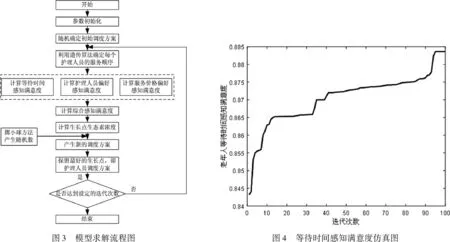
表2 最优调度方案(等待时间感知满意度目标)

(2)护理人员偏好感知满意度分析

最优调度方案如表3所示，护理人员偏好感知满意度为0.924。此时，ω1=0，ω2=1，ω3=0,λ1=1，λ2=0；大多数老年人的偏好得到了满足(灰色单元格为未满足老年人)，满足比率为94%。

(3)服务价格偏好感知满意度分析

最优调度方案如表4所示，服务价格偏好感知满意度为0.945。此时，ω1=0；ω2=0；ω3=1;λ1=1,λ2=0;大多数老年人的偏好得到了满足(灰色单元格为未满足老年人)，满足比率为97%。

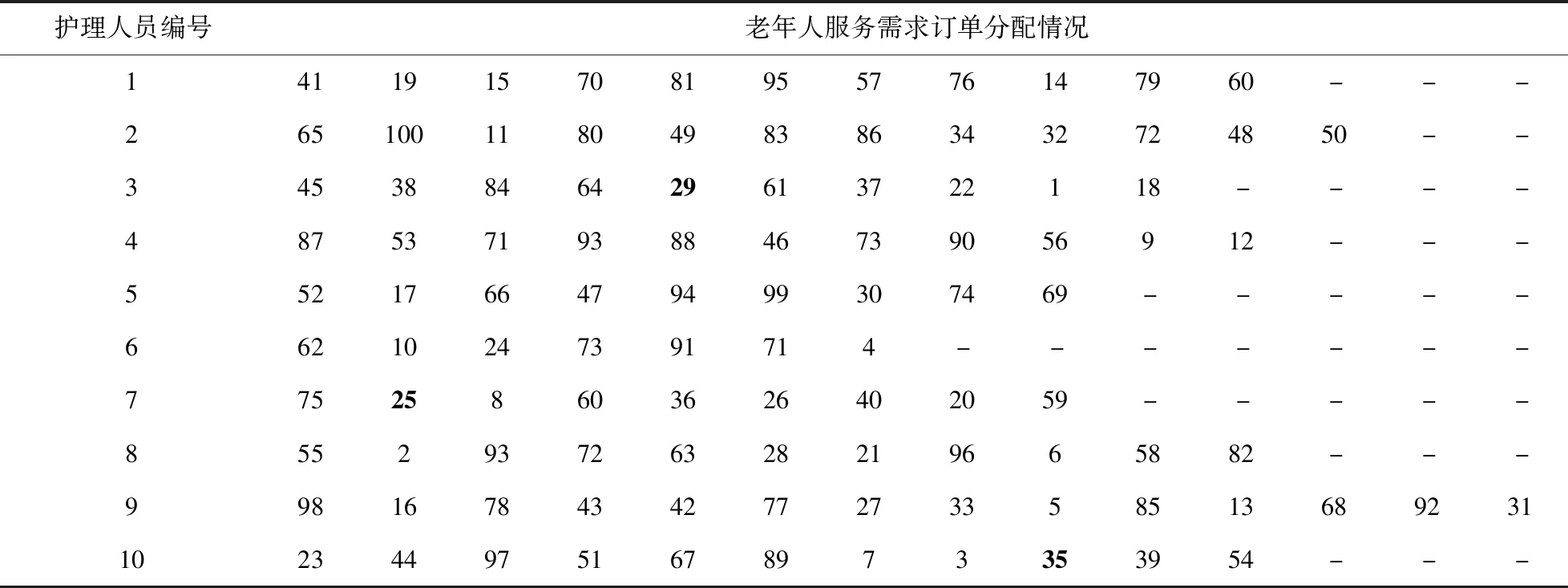
表4 最优调度方案(服务价格偏好感知满意度目标)

(4)老年人综合感知满意度分析

最优调度方案如表5所示，老年人综合感知满意度为0.921。此时，ω1=0.2566；ω2=0.5713；ω3=0.1721;λ1=1,λ2=0;；护理人员偏好比例较高为64%(灰色单元格为未满足老年人)，服务价格偏好比例为22%。这一结果的产生是由于在计算综合感知满意度时，护理人员偏好感知满意度的权重最大。

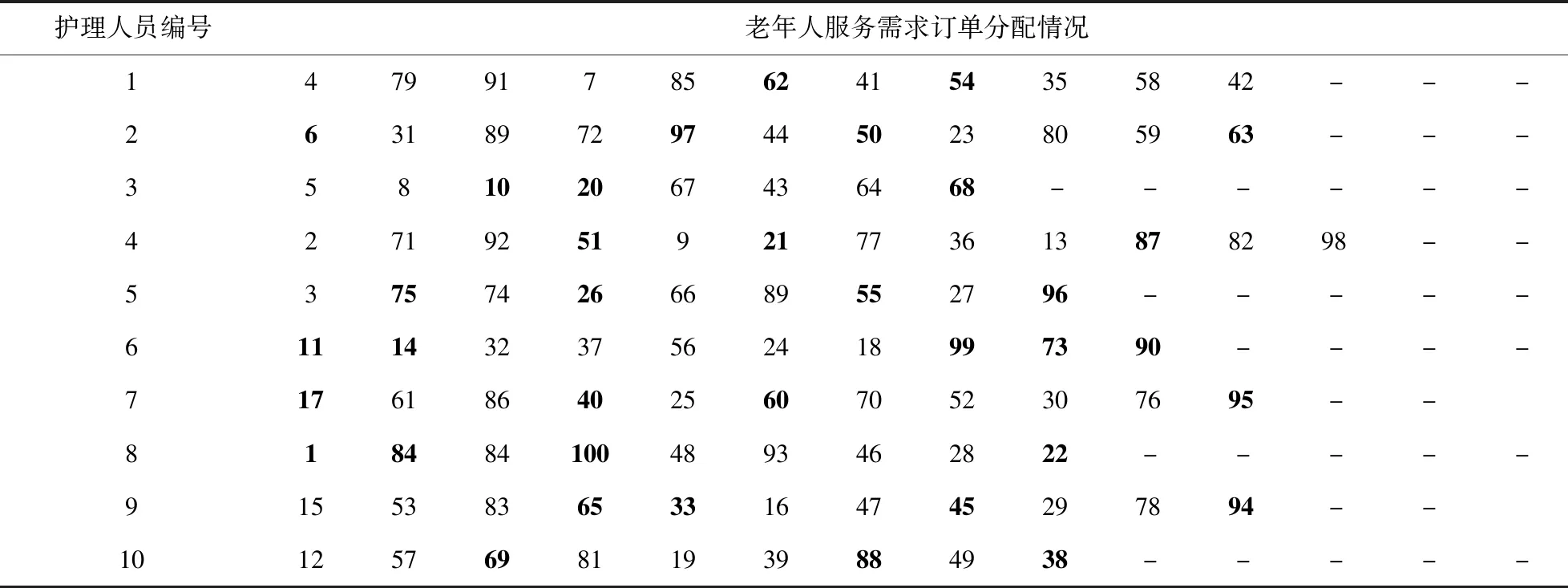
表5 最优调度方案(老年人综合感知满意度目标)

(5)护理人员调度综合满意度优化

如图5，此时，ω1=0.2566,ω2=0.5713,ω3=0.1721。在λ1>0.5的情况下，社区居家养老服务中心更倾向于老年人综合感知满意度，当护理人员数量增加，综合满意度呈现增加的变化趋势。而在λ1<0.5的情况下，更倾向于护理人员投入成本，当护理人员数量增加，综合满意度呈现减少的变化趋势。

从仿真结果可知，社区居家养老服务中心根据自身的倾向性对两个目标赋予不同的权重，同时也可以调整等待时间、护理人员偏好和服务价格偏好感知满意度在综合感知满意度中占的比重，从而满足其多维需求。

(6)算法性能分析

为进一步分析PGSA的性能，本文将其与传统优化算法——粒子群算法(PSO)进行了比较。首先设定一组特征相同的护理人员调度问题B，M为其中一个实例，M∈B，L={PGSA,PSO}，K(L,M)为某一实例M在使用算法L时多次求解的最优解平均值；OPT(M)为在该实例情况下采用两种算法求解时最优解平均值的最大值，即OPT(M)=max{K(L,M)}。此时，可用下式计算不同算法的相对特性。

利用T(L,M)记录多次采用算法L解决实例M时的CPU平均消耗时间。两种算法均使用Matlab编程，计算机CPU为32GHz，内存为8GB。对于每个实例M，每个算法运行10次，迭代次数均为100次。比较结果如表6。

表6 算法性能及平均消耗时间比较

由表中数据可知，随着求解规模扩大，PGSA在性能参数和计算时间方面的优势更加明显。

6 结论

本文从老年人满意度的角度出发，构建了主要目标为最大化老年人综合感知满意度，次要目标为最小化社区居家养老服务中心运营成本的调度优化模型，通过设计遗传算法和模拟植物生长算法进行求解并仿真，验证了模型和算法的可行性和有效性。求解结果与仿真分析表明能够保证提升老年人综合感知满意度的同时，让社区居家养老服务中心的成本得到有效控制。此外，随着老年人个体灵活性不断增加(如时间变动)，如何在更为复杂的情况下找到合理的调度策略，将作为下一步的研究方向。