心理账户、损失厌恶与行为资产配置实证研究
2022-09-13詹泽雄吴宗法
詹泽雄, 吴宗法
(1.福建工程学院 管理学院,福建 福州 350118; 2.同济大学 经济与管理学院,上海 200092)
0 引言
行为金融基于“有限理性人”假设,将投资者认知偏差与情绪因素纳入到金融投资分析中,对经典金融理论进行有效补充。Kahneman等[1]创立的前景理论通过价值函数刻画了投资者参照依赖、损失厌恶等决策特征,成为行为投资组合理论研究的基础。Barberis等[2]在前景理论的基础上采用线性价值函数研究投资者在心理账户框定下的股票回报率和动态损失厌恶下的资产配置问题;Fortin等[3,44]利用下偏矩方法构建了线性和二次损失厌恶模型,并利用美欧市场数据实证比较研究了均值方差模型、CVaR模型和线性损失厌恶投资组合模型之间的差异性;金秀等[5]基于线性损失厌恶效用函数构建动态损失厌恶构建投资组合模型并比较投资绩效;Cumova等[6]构建了基于上偏矩与下偏矩(UPM-LPM)的投资组合模型,将损失厌恶模型与均值方差模型整合到统一框架中,研究不同风险态度的变化对投资组合前沿的影响;詹泽雄等[7]等从动态参照点的角度研究非线性损失厌恶的投资组合模型资产配置;刘家和等[8]构建状态依赖下的损失厌恶投资组合模型,并在不同市场条件下实证检验模型的有效性。上述研究局限性在于都基于单一和简单的参照点,且对心理账户的框定作用考量不足。
Thaler[9]提出“享乐主义编辑假说”,认为人们在进行经济决策并非追求理性认知上的期望效用最大化,而是追求情感上的满意最大化,并进一步提出了人们在经济决策时会受限于心理账户的影响。Thaler认为心理账户可以解释金融市场“异象”(朱遥等)[10],现实中机构投资者对资产进行分层隔离管理正反映了心理账户对投资组合策略的影响。Shefrin等[11]结合SP/A理论[12]和前景理论开创了行为投资组合理论,认为投资者会将各层次的资产组合与特定的收益目标和风险态度相联系,而忽略各层次心理账户的相关性,构建一种金字塔式的行为投资组合,并对单心理账户和两个心理账户下的投资组合问题进行研究,其有效前沿呈现非凹曲线形状;Gordon等[13]讨论心理账户下组合有效前沿与均值方差模型的相似性;曹兵兵等[14]借鉴不确定决策的方法,以行为投资组合理论模型为基础,建立了多心理账户下的证券投资组合模型并进行求解;詹泽雄等[15]在均值方差模型框架下基于前景理论构建了行为投资组合,研究发现模型具有更优的性质。这些研究多基于传统投资组合模型的思路探讨心理账户对资产配置的影响,较少融入损失厌恶、参照依赖等行为特征。
现有的基于损失厌恶的行为投资组合模型多忽略心理账户的影响,而关于心理账户的投资组合研究又常忽视投资者的损失厌恶等行为偏好,因此,有必要结合心理账户的框定依赖与前景理论参照依赖进行研究。
1 理论基础
1.1 线性损失厌恶模型
累积前景理论(Kahneman等)[16]将收益和损失定义为相对于决策参照点的正负偏离程度,并通过损失厌恶系数对损失赋予更大权重,前景理论S形价值函数如下:
(1)
式中,λ≥1表示损失的厌恶程度;αβ∈(0,1],分别表示对于收益和损失的敏感性程度,体现对收益的风险规避和对损失的风险寻求特征。价值函数的凹凸性使前景理论价值函数在应用方面受到限制。在不失一般性的前提下,许多学者采用Barberis等[2]提出的线性损失厌恶模型,将价值函数的参数α和β设置为1,使分段幂效用函数转变为两段线性函数形式。
1.2 心理账户与参照点
Thaler提出心理账户(Mental Accounting)并指出人们根据资金来源、所在及其用途等因素将资金划入不同心理账户进行分类记账、编码和评估,但心理账户的划分并没有形成统一的标准。行为投资组合理论认为投资者对不同资产的收益与风险认知不同,会将不同资产划入不同评价账户,形成一种具有层次性的金字塔式投资组合,对金字塔中各层次的资产组合依据不同参照点进行独立评价。同时,关于参照点的研究进展表明,决策中的参照点并非是一成不变的且存在多个参照点(Koop等)[17]并不断更新参照点(Baucells等)[18]。关于参照点的形成和选择,王晓田等[19]提出了三参照点理论(Tri-Reference-Point Theory,TRP),将众多的参照点集成为符合人们决策心理同时被大量研究证实的三类关键性参照点,即底线(Minimum Requirement,MR)、现状(Status Quo,SQ)和目标(Goal,G),并将心理价值x划分为失败(x
2 投资组合模型
2.1 单心理账户投资组合模型
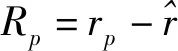
(2)

假设资产独立同分布,则在离散时间条件下,资产某一状态s(s=1,2,…,S)下的资产收益率向量为rs=[r1s,r2s,…,rns]T,则状态S下投资组合收益率为rps=wTrs;状态发生的客观概率向量为p=[p1,p2,…,pS]T,ps为状态s发生的客观概率,经前景理论权重函数调整后的主观概率为πs=π(ps)。若投资者依据资产T期历史收益率进行预测决策,每一期(t,t=1,2,…,T)的资产收益率视为一种状态s收益率,且投资者对于每期历史收益率赋予等权,即令πs=pt=1/T,则投资组合前景价值为
(3)

于是,在单心理账户框架下,投资组合决策问题可描述为
(4)
上述投资组合优化问题可以转化为关于均值与下偏矩的模型:
(5)
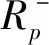
将模型(5)称为单心理账户线性损失厌恶模型(SMA)。模型表明投资者的效用或价值源自于两部分,一部分是来自于投资组合收益满足感,另一部分是损失厌恶或损失风险引起的不足。通过模型转化,上述模型有N+T个决策变量,T个不等式约束和一个等式约束的线性规划问题(Best等)[20],可求解其最优投资组合配置比例w*。
2.2 多心理账户投资组合模型

(6)
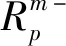
将模型(6)称为多心理账户线性损失厌恶模型(MMA)。具有多心理账户特征的行为投资者的总效用价值源自资产配置在各心理账户产生的效用的加权平均之和。通过模型转化,对于每个心理账户模型(m),都有N+T个决策变量,T个不等式约束和一个等式约束的线性规划问题,该模型一定有最优解,可求解第m个心理账户最优投资组合配置比例w(m)*和投资者最优投资策略矩阵w*。

3 实证研究
3.1 研究数据与方法
实证研究中采用中证基金指数数据进行研究,选取中证股票基金指数(H11021.CSI)、中证混合基金指数(H11022.CSI)、中证债券基金指数(H11023.CSI)和中证货币基金指数(H11025.CSI)作为构建投资组合的资产,这四类指数分别代表不同风险收益类型的资产,一般认为,股票基金具有高风险高收益特征,混合基金具有较高的风险和较高的收益,债券基金具有较低的风险和较低的收益,而货币基金是典型的低风险低收益资产。收益率计算公式为rt=Pt/Pt-1-1,pt为t期资产收盘价格指数。数据的选取区间为2007年1月到2019年6月共计150个月,估计期内市场经历了上升、下降、盘整等状态。所有数据来自Resset数据库。
对模型进行最优化求解时,采用的Out-of-Sample Evaluation(OSE)方法,假设投资者每月进行一次投资决策,在采取全样本进行估计时,投资者基于资产过去12期(一年)的历史收益率进行预测决策并构建投资组合,在考察期内依据此方式滚动更新投资决策。因此,可以得到2008年1月到2019年6月共计138期的最优投资组合配置,依据这138期最优投资组合配置比例可以得到不同资产的多期平均最优配置比例。为了更全面比较不同投资组合模型在不同参数与市场条件下的绩效表现,引入常用的投资绩效评价指标夏普比率(Sharpe Ratio)、信息比率(Information Ratio)、索提诺比率(Sortino Ratio)和欧米茄比率(Omega Ratio),对不同投资组合模型进行进一步考察。在计算上述评价指标时,分别采用无风险收益率和市场收益率作为基准收益率水平,其中,无风险收益率数据来源于Resset数据库的月无风险收益率,市场收益率采用上证综指收益率(SH000001),以便从不同程度和角度比较模型的有效性。
考察期内市场经历了上升、下降、盘整等阶段,针对不同状态下的市场投资者应调整投资策略,在市场处于上升阶段应投资于高收益资产以求得超额收益,而在市场处于下降阶段应投资于较为稳健的资产以规避市场风险。因此,根据考察期内上证综指(SH000001)收盘价,以七分位数和三分位数将考察期内的资产收益数据分为上升、盘整、下降三类市场状态①,假设投资这每月进行一次投资决策,在采取分阶段样本进行估计时,投资者基于资产过去6期(半年)的历史收益率进行预测决策并构建投资组合,考察不同市场状态下的投资组合决策与绩效。
实证研究中还将线性损失厌恶模型与传统投资组合模型进行比较研究。
3.2 模型设定与参数
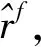
本文主要数据描述性统计如表1所示。
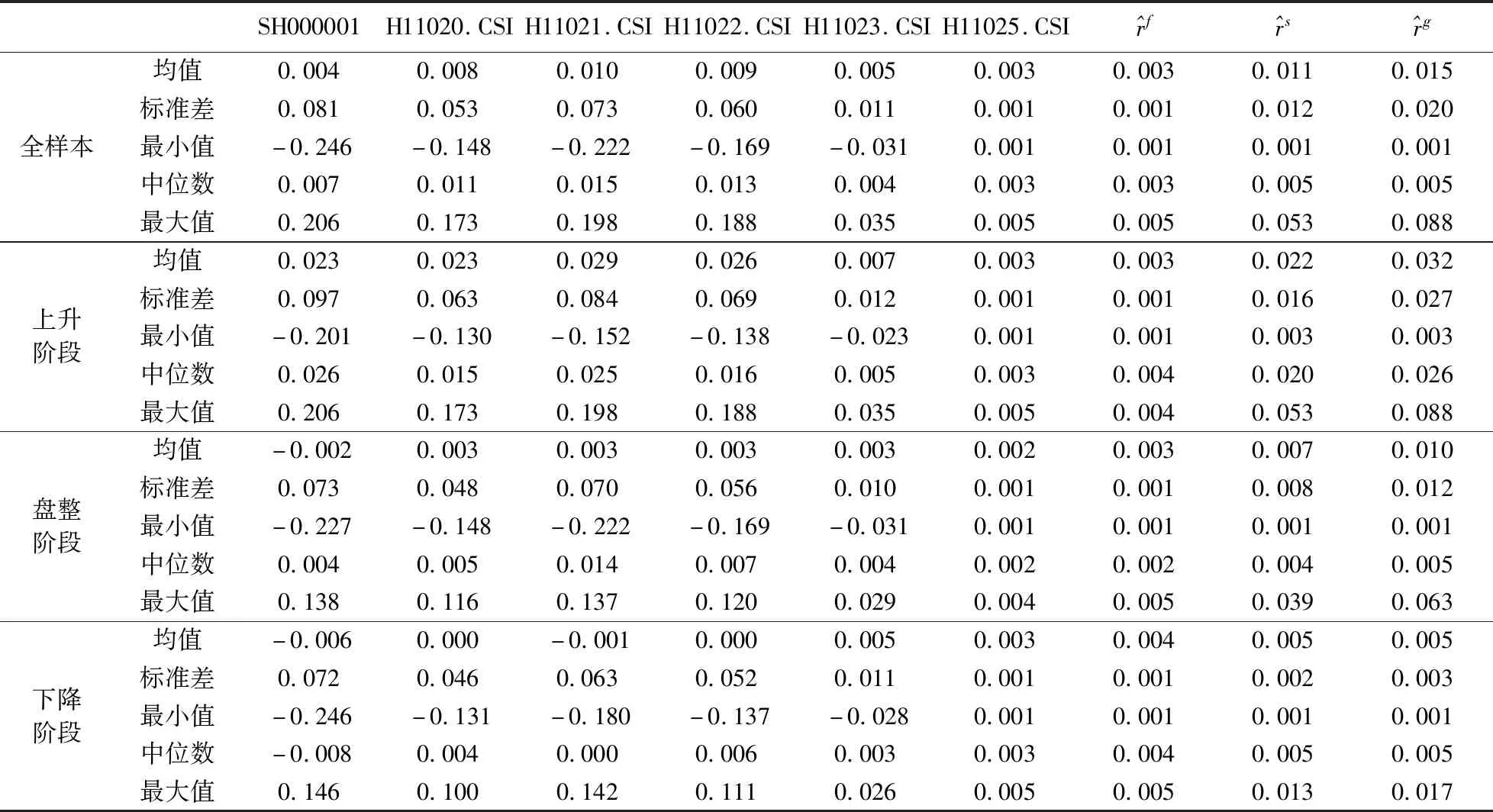
表1 数据描述性统计
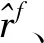
Kahneman和Tversky实验研究得出损失厌恶系数λ为2.25。实证研究中以2.25为中间值,在SMA模型和MMA模型中分别取λ等于1.5、2、2.25、3、4、5进行优化计算,以考察损失厌恶系数对行为投资者决策的影响。
综上,实证研究中构建了均值方差模型(MV)、均值半方差模型(MSV)、条件风险价值模型(CVaR)等传统模型和单心理账户(SMA)与三心理账户(MMA)两类损失厌恶模型,传统模型的期望目标收益率采用每次估计时构建投资组合的资产历史收益率的平均值,CVaR模型的置信水平设定为0.95,对于两类线性损失厌恶模型设置了6个不同损失厌恶系数,同时在SMA模型中考察三类参照点对投资组合的影响,在MMA模型中考虑不同账户权重的影响,并利用市场整体数据和上升、下降、盘整等三种状态数据对模型的投资策略与绩效进行研究。
3.3 实证研究结果
(1)最优配置比例
表2报告了传统投资组合模型与单心理账户投资组合模型最优配置比例。总体上,MV和MSV模型倾向于配置中低风险债券基金和货币基金(H11023.CSI、H11025.CSI),配置比重超过65%,CVaR模型相对MV和MSV模型增加了对高收益的股票基金(H11021.CSI)的配置比重,各类资产在不同市场条件下配置差异性不大。SMA模型在不同市场条件下呈现较为显著的差异,在上升阶段,采用不同参照点的SMA对高收益的股票基金(H11021.CSI)的配置比重均超过45%;盘整和下降阶段,对于中低风险资产(H11023.CSI、H11025.CSI)配置比重超过75%,显著高于传统模型,呈现典型的损失厌恶和风险规避特征;利用全样本对SMA进行估计,也具有与盘整和下降阶段相似的配置特征。在SMA模型中,随着参照点的提高,高风险股票基金(H11021.CSI)的配置比重逐步提高,低风险货币基金(H11025.CSI)的配置比重逐步降低,表明投资者参照点的提高会增加其对高风险高收益资产的偏好。

表2 传统投资组合模型与单心理账户投资组合模型最优配置比例
在对SMA模型和MMA模型进行实证研究时,分别对损失厌恶系数等于1.5、2、2.25、3、4、5等六种不同损失厌恶程度进行优化计算(限于篇幅,仅报告λ=2.25和不同损失厌恶系数最优权重的均值),发现不论是在单心理账户还是多心理账户框架下,其他条件既定,遵循线性损失厌恶进行投资决策的行为投资者,其最优投资策略随着λ的增大而趋向于保守,即损失厌恶系数越大行为投资者配置于高风险资产的比例降低而配置于低风险资产的比例相应上升。
表3报告了不同的心理账户资金配置策略下行为投资者最优资产配置比例,同一策略下账户间资金配置比例影响投资者的资产选择偏好,当投资者更加关注安全性时,对安全性账户配置高比例资金(MMA6:3:1或MMA6:1:3),其在风险较低的资产上配置比例会显著提高;但当投资者对现状潜力或抱负水平账户配置较高比例资金时(如MMA3:6:1或MMA1:3:6),各类资产配置比例差异不显著,这说明采用MMA模型的投资者即使对实现潜力或抱负水平具有追求,但其决策依然遵循“安全第一”,这也体现了多心理账户线性损失厌恶模型对投资者多样投资目标兼顾的内在本质。实证研究还对心理账户资金按照50%:30%:20%、50%:20%:30%、30%:50%:20%、30%:20%:50%、20%:50%:30%、20%:30%:50%配置,验证了上述结果的稳健性。因此MMA模型在配置中呈现典型的分散和均衡配置特征。同时,损失厌恶系数越大投资者配置于高风险高收益资产的比例降低而配置于低风险低收益资产的比例相应上升,这与前景理论揭示的投资者风险态度一致。与SMA模型相比,利用全样本估计的MMA模型资产最优配置策略更为均衡,反映多心理账户框架下对安全性、潜力、抱负三者的兼顾;在市场上升阶段,MMA模型与SMA模型相同,具有积极的投资策略,寻求高收益资产配置,但MMA模型对于高风险高收益的股票基金(H11021.CSI)的配置比重显著高于SMA模型,呈现更为激进的投资策略特征;而在市场盘整和下降阶段,两者具有相同的避险选择,但SMA模型倾向于对低风险资产进行大量配置,而MMA模型是分散平均的配置策略。

表3 三心理账户投资组合模型最优配置比例
(2)投资组合绩效评价
表4报告了传统投资组合模型和线性损失厌恶模型在不同损失厌恶系数条件下绩效指标的均值。从夏普比率来看,线性损失厌恶模型略相较于传统模型具有更高的收益均值,特别是市场处于上升阶段,MMA收益均值显著高于传统模型;当市场处于盘整和下降阶段,SMA模型略优于传统模型。信息比率、索提诺比率和欧米茄比率是基于下侧风险思想的绩效指标,当市场处于盘整和下降阶段,SMA模型绩效指标显著提高,说明关注下侧损失风险的线性损失厌恶模型在盘整和下降阶段配置策略更有效率,而MMA各项指标表现均较为稳健,这是由MMA在资产配置策略上呈分散均衡配置的特征导致。从信息比率看,线性损失厌恶模型的信息比率总体上高于传统模型,特别是MMA模型在各市场状态下显著优于传统模型,SMA模型的信息比率随参照点的提升而提高;从索提诺比率和欧米茄比率来看,用全样本和上升阶段估计,SMA模型的索提诺比率和欧米茄比率随参照点的提升而提高,而在盘整和下降阶段则随参照点的提高略有降低,但SMA模型相较于MMA模型和传统模型仍具有显著的优势。
表4还报告了MMA模型三种心理账户资金配置策略(MMA6:3:1,MMA3:6:1,MMA1:3:6)下资产配置绩效。结果显示,上升阶段对于较低层次心理账户更为关注的投资者能取得更好的绩效表现,而在盘整和下降阶段对于中高层次心理账户更为关注的投资者能取得更好绩效表现。研究中,在计算信息比率、索提诺比率和欧米茄比率时,还采用无风险收益率作为基准水平(限于篇幅,未在表中报告),其总体结论与采用上证综指收益率作为基准水平计算的结果相似。
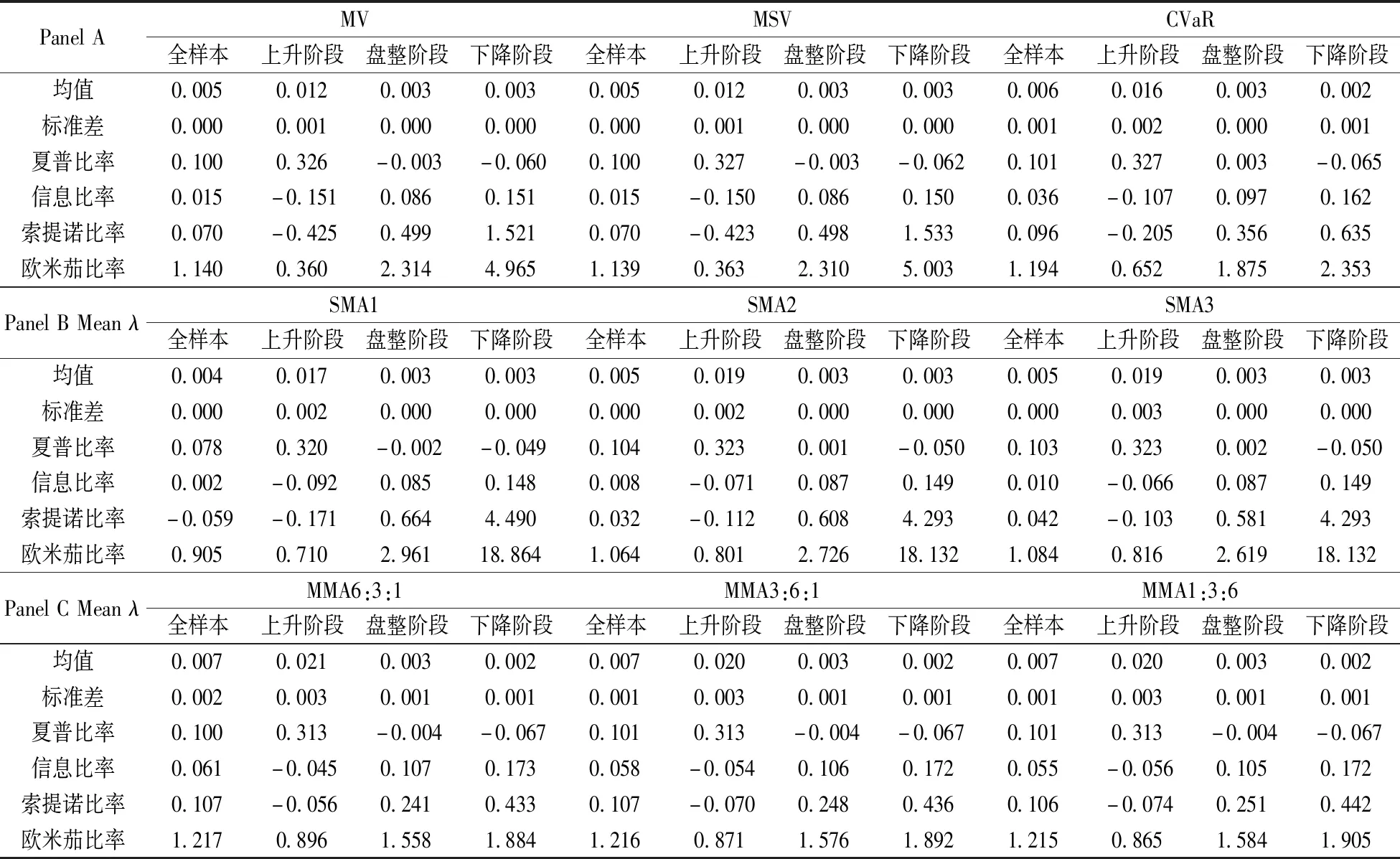
表4 投资组合模型绩效指标
3.4 结论
实证研究表明,(1)相较于传统模型,线性模型更加关注下侧损失风险,更偏好收益较好而下侧损失较小的资产;(2)越注重安全性的投资者越偏好低风险资产,而寻求实现抱负水平的投资者更偏好高收益资产,但依然遵循“安全第一”的投资准则;(3)采用线性损失厌恶模型决策,损失厌恶系数越大,配置于高风险高收益资产的比例降低而低风险低收益资产的比例相应上升;(4)在市场上升时,MMA模型与SMA模型均采用积极的投资策略,在市场下降时,两者都趋于保守,MMA模型呈现分散均衡配置的特征;(5)遵循线性损失厌恶模型进行投资决策时,适度提升目标寻求减小风险厌恶,有助于取得更好的投资绩效。
4 结语
损失厌恶与心理账户是行为金融的核心发现,当前对心理账户框架下的资产配置研究尚不够丰富。本文借鉴前景理论相关研究模型,结合SP/A理论和三参照点理论建立单心理账户和三心理账户线性损失厌恶行为投资组合模型。实证研究中利用不同市场状态下的中证基金指数数据考察了不同损失厌恶系数、不同参照点、不同心理账户资金配置在不同市场状态下的最优资产配置策略和投资组合绩效,并与传统的投资组合模型进行比较,研究发现依据线性损失厌恶模型进行决策的行为投资者更加关注下侧损失风险,具有多心理账户框架的行为投资者关注潜力寻求和抱负实现的同时,也更注重投资的安全性。
