增量式Huber-支持向量回归机算法研究

周晓剑, 肖 丹, 付 裕

(1.南京邮电大学 管理学院,江苏 南京 210023; 2.厦门大学 信息学院,福建 厦门 361005)

0 引言

支持向量机(Support Vector Machine，SVM)是数据挖掘中的一项重要的技术，由Vapnik于20世纪90年代年首先提出的，是建立在统计学习理论(Statistical Learning Theory，SLT)中的VC维理论以及结构风险最小化原则的基础之上的，它的本质是求解凸二次规划问题，与传统的学习方法相比，支持向量机在解决小样本、非线性和高维分类问题中有显著的优势[1～3]。

支持向量回归机(Support Vector Regression，SVR)是支持向量机(SVM)用于解决回归问题的推广形式。样本训练时，随着样本数的增加，学习难度逐渐增大[4]。在实际的回归问题中，样本通常是增量在线提供的，此时，若采用SVR一次性建模算法，每当样本数据集变动，即使只是增加一个样本，均需要从头开始学习、重新建模，但是这样建模成本较高[5]。与之不同的是，增量式算法的学习过程不是一次离线完成的，而是逐一加入数据不断优化的过程，在处理新增样本时，不用重新建模即可完成新数据的学习[6]。

SVR的增量算法通常基于ε-不敏感损失函数，即增量式ε-SVR算法[7]。ε-不敏感损失函数潜在的缺点是它对大的异常值非常敏感，而Huber损失函数对噪声的容忍能力较强，能够较好地抑制异常值对计算结果的影响，所以在有噪声的情况下Huber损失函数是比ε-不敏感损失函数更好的选择[8,9]。周晓剑等[10]研究了一种新的SMO算法，用于求解非半正定核Huber-SVR问题。为使Huber-SVR更具鲁棒性，周晓剑等[11]还深入研究了Huber-SVR中参数与输入噪声之间的关系。由于Huber-SVR具有更强的鲁棒性和建模性能，本文提出了一种基于Huber损失函数的增量式Huber-SVR算法，该算法能够连续不断地将新样本的信息集成到之前已经训练好了的模型中，而不是对所有样本重新建模，极大地提高了建模效率。

本文第二部分首先介绍了Huber-SVR的基本形式以及求解此问题的最优化条件即KKT条件；第三部分重点阐述了增量式Huber-SVR算法的数学原理以及具体的算法步骤；第四部分是实验部分，通过对比增量式Huber-SVR算法，增量式ε-SVR算法和增量式RBF算法对四个真实样本数据集的回归预测来验证本文所提算法。最后得出结论：增量式Huber-SVR算法对真实数据的回归预测精度比另外两种算法更高；第五部分对本文所做研究进行了总结，并对今后研究方向进行了展望。

1 Huber-SVR基本形式和KKT条件

1.1 Huber-SVR基本形式

(1)Huber损失函数[12]：

(1)

其中μ为损失函数的参数，ξ为真实值与预测值之间的偏差。

(2)Huber-SVR原始问题：

数据集T={(xI,yI),…,(xI,yI)}中xi是输入，yi是输出，线性回归问题的目标就是寻找空间Rn×Rn上的一个超平面f(x)=wTΦ(x)+b，其中：输入xi被函数Φ映射到一个高维再生核希尔伯特空间，w是权系数向量，b是偏置，使得超平面与训练样本集T中训练样本点的偏离最小。

当SVR中的损失函数取Huber损失函数时，就构成了Huber-支持向量回归机。Huber-支持向量回归机(Huber-SVR)的原始问题如下:

(2)

其中(*)是变量有*符号或没有*符号的缩写，ξ(*)是非负松弛变量，C是惩罚参数。

(3)Huber-SVR对偶模型:

利用对偶模型，引入朗格朗日乘子求解原问题，对偶问题如下：

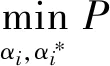
(3)

其中Qij=Φ(xi)TΦ(xj)=K(xi,xj)，K是核函数，回归方程可以写为：

(4)

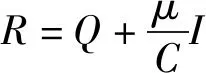
(5)

把式(3)化简为:

(6)

根据凸优化理论，式(6)等价于如下的拉格朗日函数:

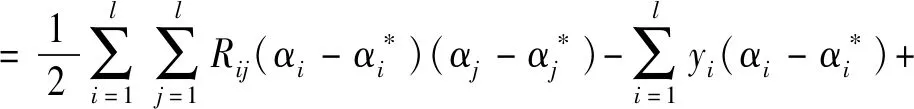
(7)

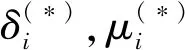
1.2 KKT条件

根据凸最优化理论，式(7)解的充要条件，KKT条件如下:

(8)

(9)

函数间隔：

(10)

由(8)，(9)，(10)得:

(11)

2 增量式Huber-SVR算法

增量算法思想：新增样本xC，先判断新样本xC是否满足KKT条件，如果满足，则把xC加入相应的集合，结束；如果xC不满足KKT条件：然后不断改变新样本xC的值，直到新样本xC满足KKT条件，同时原训练集中的所有样本也满足KKT条件。

新样本xC的θC影响着原样本的θi和h(xi)，所以xC的加入可能会使一些样本发生移动，不满足原集合的KKT条件，但满足另一集合的KKT条件。

2.1 增量关系

本小节介绍的是增量ΔθC发生变化时，而没有引起样本在S集，E1集和E2集之间移动时，增量ΔθC和与Δh(xi)和Δθi之间的关系。

由式子(10)得:

(12)

(13)

i∈S时，要保持样本不发生移动，h(xi)≡0，所以由(12),(13)得:

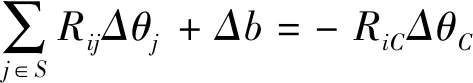
(14)

S中的样本:S={s1,s2,…,sS}

(15)

把(14)用矩阵形式表示如下:

(16)

(17)

(18)

令：

H=R-1

(19)

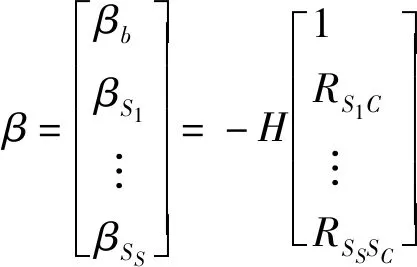
(20)

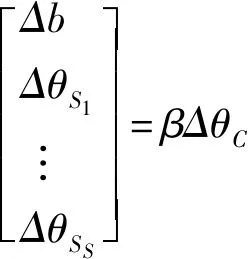
(21)

即:

Δb=βbΔθC

(22)

Δθj=βjΔθC,∀j∈s

(23)

Δh(xj)=0,∀j∈s

(24)

从式子(22)，(23)可以看出当时，ΔθC是如何影响Δθi和Δb的值。把(23)扩展到所有样本时，因为E1和E2中的θ值为常数，所以i∉S时，Δθi=0，因此(21)式隐含着，当i∉S时，βi≡0。

当i∉S时，定义集合N:

N=EI∪E2={n1,n2,…,nn}

(25)

由式子(11)(12)(21)可知:

(26)

所以，令:

(27)

最后得到:

(28)

Δθi=0,i∉S

(29)

当i∈S时，Δh(xi)=0，所以γ≡0。

当S是空集时，根据式子(12)，(13)，(27)得:

Δh(xn)=Δb,n∈E1∪E2

(30)

由以上分析可知：当新样xC加入，没有引起其他集合中样本发生移动时：

知道ΔθC的值，根据式子(22)(23)得知，当i∈S时，可以更新训练集S中样本i的和b的值，同时，Δh(xi)=0；给定ΔθC的值，由式(28)，(29)可知，当i∉S时，可更新样本i的h(xi)，同时，Δθi=0。

2.2 样本的移动

在θC不断变化的过程中，随着ΔθC的变化，Δθi，Δh(i)也在随之变化，当ΔθC到达一个临界值时，会使得样本在S集，E1集，E2集中相互移动，导致各集合中组成分发生变动。为了解决这个问题，采取的措施是，求得ΔθC变动引起样本在S集，E1和E2集中变化的最小值，使得每次只有一个样本在集合之间移动，即求得最小调整增量ΔθC。

具体需要考虑以下几种情况：

情况1新样本xC满足KKT条件

(1)xC加入S集：

(31)

(2)xC加入E1集:

(32)

(3)xC加入E2集

(33)

情况2i∈S，样本点从S集移到E1集或者E2集，分别是:

(1)样本点从S集移到E1集:

Δθi=C-θi

(34)

(2)样本点从S集移到E2集

Δθi=-C-θi

(35)

样本点从S集移到E1集时，这些样本的θi值会逐渐增加到边界值C；样本点从S集移到E2集，这些样本的θi值会逐渐减小到边界值-C;

(36)

情况3i∉S，样本点从E1集或者E2集移到S集：

样本点移到S集合时，最终h(xi)=0，所以:

(37)

最后，结合三种情况计算当只有一个样本点在集合之间移动时的最小增量ΔθC:

q=sign(-h(xC))

(38)

(39)

2.3 逆矩阵的更新

定义(S+1)×(S+1)维分块矩阵B:

(40)

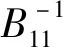
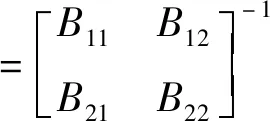
(41)

根据分块矩阵求逆的方法，集合S中增加一个样本xt时，矩阵更新如下：

(1)第一个样本更新如下:

(42)

(2)向H中继续增加新样本，更新如下:

(43)

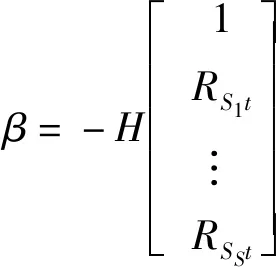
(44)

γt=Rtt+[1RS1t…RSSt]β

(45)

当新样本加入S集合时，β的更新如式子(19)所示，γt是式子(27)中γ的最后一个元素。

(3)集合S中减少一个样本点时，矩阵更新如下:

(46)

当索引i、j为0时，指的是b这一项。

2.4 算法初始化

本文增量算法模型的构建是通过两个样本建立最初的模型，然后在此基础上进行模型的更新。初始模型建立使用增量算法，即从头开始使用增量算法提供完整的解决方案。给定两个样本训练集，表示为：T={(x1,y1),(x2,y2)}，且y1≥y2，对偶问题式子(6)的解如下:

(47)

θ2=-θ1

(48)

b=(y1-y2)/2

(49)

2.5 算法步骤

增量式Huber-SVR算法:

输入：

数据集T={(x1,y1),…,(xl,yl)};

系数{θi,i=1,2,…,l},和h(xi)偏置b；

将样本分成S集，E1集和E2集；

矩阵H；

新样本xC。

输出：

新的系数θi,h(xi),i=1,2,…,l以及θC，h(xC)和偏置b；

更新后得到的新的S集，E1集和E2集；

更新后的矩阵H。

算法步骤：

1、初始化令θC=0；

2、计算h(xC)；

3、如果h(xC)=0，把新样本加入到S集，更新矩阵H，结束；

4、如果新样本不满足KKT条件：

(1)令q=sign-(h(xC)),计算最小增量ΔθC，使得恰有一个样本在S集，E1集和E2集之间移动。

(2)做如下更新：

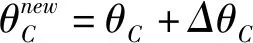
直到满足下列条件之一：

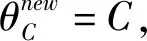
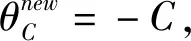
③原训练集中的一个样本i发生移动：

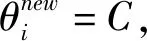
如果h(xi)new=0，则把样本从E1集或E2集移入S集。

更新矩阵H；

5、返回4。

6、算法结束后输出h(xC)，b，θC，θi，h(xi),i=1,2,…,l矩阵H，S集，E1集和E2集。

3 实验及其结果

3.1 实验目的

验证本文提出的增量式Huber-SVR算法的可行性，将该算法与应用较广泛的增量式ε-SVR算法和文献13中的增量式RBF学习算法[13]进行比较，将三种算法应用于实际数据中，比较三种算法的预测性能。

3.2 实验设计

本实验选取的数据来源于UCI机器学习存储库，有“翼型自噪声数据集”，来自西班牙北部的“葡萄酒质量数据集”，“联合循环电厂数据集”和“QSAR水生毒性数据集”。“翼型自噪声数据集”共1503条数据，每条数据包括5个输入变量，输出变量是：压缩的声压级。“葡萄酒质量数据集”删除重复样本后包括1359条红葡萄酒样品数据，输出变量是：葡萄酒质量得分。“联合循环电厂数据集”用来预测工厂的每小时净电能输出(EP)。“QSAR水生毒性数据集”用于预测对水蚤的急性水生毒性定量响应。

实验中，用以上四个数据集分别进行建模，对增量式Huber-SVR算法，增量式ε-SVR算法和增量式RBF算法的拟合程度进行测试，总共分为12种情形。每次建模时，在样本数据集中随机抽取150个样本，其中前100个样本作为训练样本，剩余的50个样本作为预测的测试样本。为了避免偶然因素的影响，在这12种情形下，每种情形分别重复试验200次，再对200次的平均结果进行比较，比较三种增量式算法的预测性能。

3.3 实验结果与分析

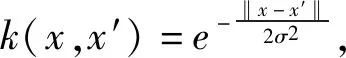
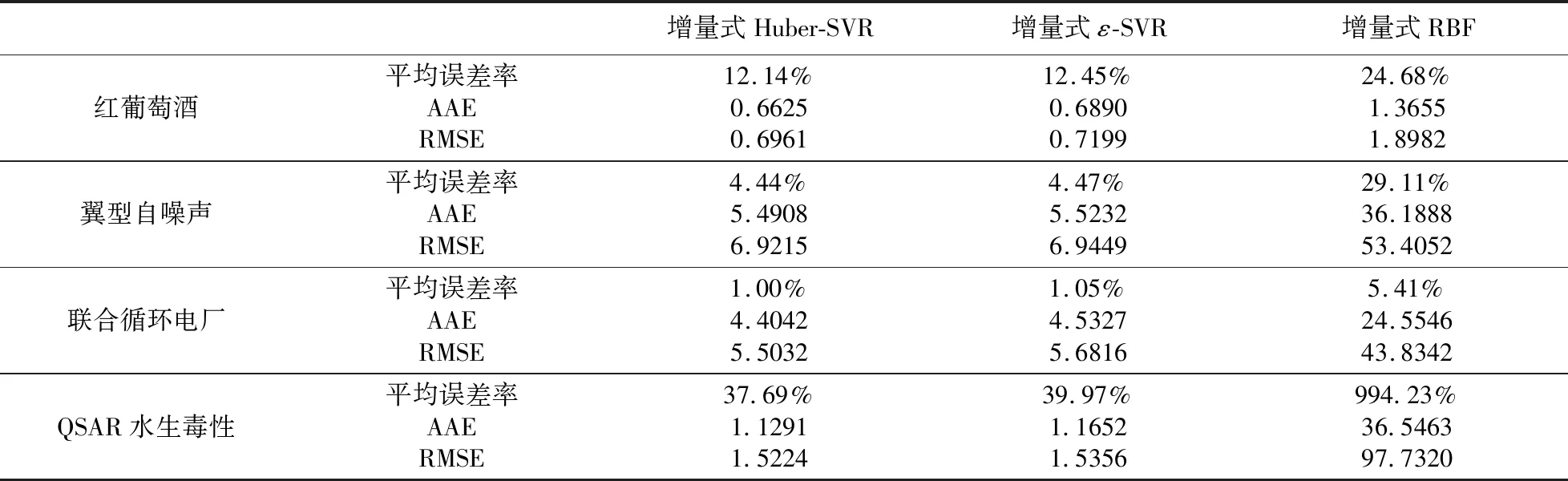
表1 增量式Huber-SVR、增量式ε-SVR和增量式RBF算法预测结果比较

设真实值为y，预测值为f(x)。

(1)平均误差率：

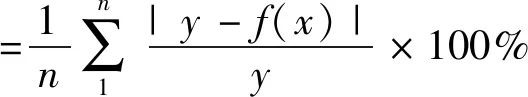
(2)平均绝对误差:

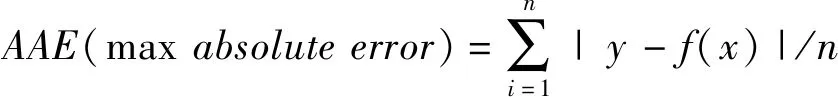
(3)均方根误差：

从表1中的误差分析可以看出：在这四组实验中，增量式Huber-SVR算法的平均误差率以及AAE和RMSE三项指标均小于增量式ε-SVR算法和增量式RBF算法中对应的数值；这是因为相对于ε-不敏感损失函数，Huber损失函数更适用于预测数据有噪声的情况，而真实的数据常常是有噪声的，这在实验结果当中得到了验证。而增量式RBF学习算法对真实数据进行回归预测时，预测精度明显低于两种增量式SVR算法。所以在用增量式Huber-SVR进行回归预测时，预测的误差率更小，精度也更高。这也更加说明了研究增量式Huber-SVR算法的必要性和该算法的有效性。

4 结论

增量式Huber-SVR算法在预测样本数据集发生变动时，能够在预测过程中及时对模型中的参数进行修正，在之前已经建立好了的模型上逐步更新，就能够得到结果。该模型结合了Huber损失函数的优点：当训练样本数据分布未知时，Huber损失函数具有鲁棒性，同时在有噪声的情况下Huber损失函数是比ε损失函数更好的选择。本文将增量式Huber-SVR算法，应用最为广泛的增量式ε-SVR算法和增量式RBF算法应用于实际数据中进行比较。实验结果表明，在对真实的数据进行回归预测时，增量式Huber-SVR算法对真实数据的拟合程度更好，回归预测精度更高，误差率也较小。增量式Huber-SVR算法的建模虽然取得了一定的成果，但当训练数据不断增加到一定程度时，运用增量式算法进行回归预测，可能会出现困难。今后的研究可以考虑在样本的训练过程中增加一个新样本的同时删减一个旧样本，实现Huber-SVR的在线学习。