乘客到达时间不确定的机场动态拼车策略与算法研究
2022-09-13晏鹏宇张逸冰殷允强
晏鹏宇, 张逸冰, 殷允强
(1.电子科技大学 长三角研究院(湖州),浙江 湖州 313001; 2.电子科技大学 管理与经济学院,四川 成都 611731)
0 引言
在智慧交通和共享经济的迅猛发展下,在线拼车模式(Online Ride-sharing)在我国和欧美国家逐渐流行。在该模式下,乘客通过智能手机将出行需求实时发送至在线拼车平台。平台收到订单后,将多个具有相似出行路线和出发时间的乘客匹配在一起,指派同一辆网约车接送乘客。相对于公交地铁等公共交通方式,该模式为乘客提供更加舒适和个性化的出行服务;而相对于传统出租车和网约专车,该模式可提高车辆利用率,降低乘客出行成本,同时对缓解城市交通拥堵和减少环境污染等方面具有积极作用[1]。
机场作为城市重要交通枢纽,具有客流量大,位置相对偏远和往返机场交通成本高等特点,并且机场乘客具有大致相似的出行路线。这些特点和因素更能促成乘客的拼车匹配,为在线拼车模式提供了良好的应用场景。目前,已经有部分互联网出行平台和航空公司推出了机场前往市区的拼车服务,如四川航空公司在成都等多个城市推出的“铁航专线”服务。由于乘客到达机场拼车服务点的时间具有不确定性,机场在线拼车运作优化属于复杂的随机动态优化问题。在实际运营中,由于缺乏科学的乘客匹配策略和网约车路径规划方法,导致乘客在拼车服务点等待时间过长和网约车绕路行驶成本高等突出问题。由此,本文针对机场在线拼车模式,提出动态环境下机场拼车匹配策略和车辆路径规划算法,以提高在线拼车平台的服务水平并降低运营成本。
目前针对在线拼车模式,研究者分别提出了考虑接送乘客的时间窗、车辆容量以及绕路距离等约束的匹配策略与路径规划算法[2,3]。这些研究针对城市内拼车场景,乘客匹配策略主要根据第一位乘客的路线,沿途匹配其他乘客,并且要求乘客必须提前到达拼车点等候。针对机场在线拼车,部分文献将机场拼车点视作多车辆路径规划(MVRP)问题中的固定车场(depot),乘客目的地为交通网络中需要访问的服务点,而订单中乘客数量则对应于服务点需要配送货物数量[4],但未考虑乘客到达的随机性。目前有关动态MVRP的研究主要关注车辆随机行驶时间[5],服务点随机需求量[6],顾客订单随机到达[7]等以及多种随机因素的组合[8]。然而,通过对实际机场拼车平台运营数据分析发现,乘客到达拼车点的时间具有不确定性。这类随机因素可视为MVRP问题中运送货物(乘客)在车场的释放时间(releasing time)的不确定性,目前尚未引起足够重视[9]。此外,在优化目标上,除了需要优化车辆行驶成本外,还需要尽量减少乘客在机场拼车点的等待时间。
针对动态MVRP问题,大部分文献提出了基于随机优化[10,11]和智能启发式[12,13]的求解算法。差分进化(Differential Evolution,DE)除了具有遗传算法诸多优点外,在连续空间优化中具有更强的鲁棒性[14]。然而,DE算法基于实数对进化个体进行编码和解码,主要用于求解连续优化问题。文献[15]直接采用实数编码方式,根据进化个体基因中的整数部分指派订单到不同的车辆,并根据小数部分的大小排序安排具体的配送顺序。然而基于实数编码的算法搜索范围过大,在求解过程中可能存在大量不可行解。文献[16]采用序数编码方法构造进化个体基因,运用基于整数序规范(Integer Order Criterion, IOR)的辅助算子将差分变异操作后的实数转化为整数,使之能继续进行交叉和选择操作。在上述DE算法的个体解码方法中,根据车辆装载容量约束分配车辆,这种方法能够有效提高车辆利用率,适用于货物配送问题。而在本文所研究的机场拼车问题中,需要同时权衡车辆利用率和乘客等待时间。
基于文献回顾和实际问题背景,本文首先提出前瞻式乘客动态匹配策略,建立联合未来和已到达乘客订单信息的两阶段随机规划模型。为了高效求解模型,提出结合航班实时信息的乘客到达时间贝叶斯估计。在网约车路径规划中,开发了基于序数编码的DE算法,设计出基于订单相似度的进化个体解码规则。最后,利用真实订单数据建立仿真实验平台,验证了匹配策略在降低乘客等待时间和网约车行驶成本方面,均优于实际采用的两种匹配策略,相比文献[15,16],本文提出的改进DE算法可明显提高解的质量。
1 问题描述
本文研究的机场在线拼车平台的运作流程,如图1所示。

机场在线拼车平台每日有限的运营周期内需要在时刻t,t∈{1,,2,…,T},根据订单集合Gt决策当前需要匹配出发的订单集合Xt,Xt⊆Gt,并规划网约车运送Xt中乘客的拼车路线,以最小化乘客在拼车点的等待时间和网约车的行驶的总成本。该问题属于多阶段随机规划问题,决策Xt不仅决定当前时刻t的运作成本F(Xt),而且还影响后续运作周期的成本。由此,本文将首先提出考虑未来到达乘客的前瞻式动态匹配策略,建立两阶段随机规划模型。
3 前瞻式动态匹配策略与模型
3.1 匹配策略设计
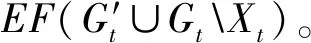

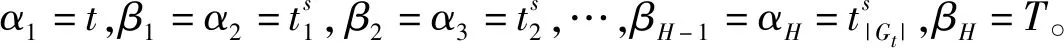



ModelPS

(1)
s.t.Xt⊆Gt
(2)

3.2 基于乘客期望到达时间的情景空间压缩

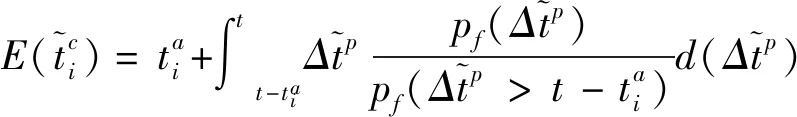
(3)
3.3 近似最优确定性模型
利用3.2节贝叶斯估计的乘客期望到达时间,可将随机规划模型PS转为确定性乘客匹配与车辆路径规划模型PD,其中0-1整数决策变量xi,j,k=1表示订单i和j匹配到车辆k,并且车辆完成订单i的运送后立即开始订单j的运送;实数决策变量tk表示车辆k的发车时间。
ModelPD

(4)
(12)
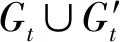
4 改进差分进化(DE)算法
模型PD为经典MVRP问题拓展,具有NP-难特性。本节首先提出基于乘客目的地和到达拼车点时间两个维度的订单相似度计算方法,并基于此设计改进DE算法中进化个体解码方式和初始种群产生方法,从而提高DE算法搜索到近似最优解的效率与质量。
4.1 订单相似度计算
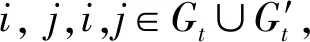
(13)
(14)
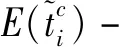
由此,考虑上述时空维度的订单相似度Ii,j为:
(15)
上式中ω为时间相似度相对权重,当两个订单之间的到达时间间隔大于Δtw时,有Ii,j=0。
4.2 进化个体编码与解码
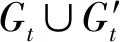

Algorithm1:基于订单相似度个体基因序列解码初始化:车辆k=1并且设置车辆k的当前容量vk=m[1],发车时间tk=tForn=2,…,N-1do Ifvk+m[n]⩽gkThen 在区间(0,1]内随机生成实数γ Ifγ>1-I[n-1],[n]Thenvk=vk+m[n] Iftk 对于基因序列Z,相邻基因对应的订单相似度越大,则被拆分的概率就越低,对应的解码方案质量也就越好。为保证解码质量,避免剔除优良子代,对每个个体的基因序列可重复进行多次解码并比较对应解码方案的适应度,选择适应度高的方案作为个体最终解码方案。通过这种邻域搜索方法,可在满足车辆装载量约束的条件下有效提高个体解码方案质量,并能有效增强种群多样性。 在初始种群产生中,利用订单之间的相似度,按照下面Algorithm 2步骤产生初始个体。该方法能够保证相似度较高的基因个体有更大的概率匹配到一起,从而有效提高初始种群质量。 Algorithm2:基于订单相似度的初始个体产生在N个订单中随机选出订单i作为个体基因序列的第1位,即基因[1]=订单i,并将订单i添加至已选择集合S;Fork=2,…,|Gt∪Gt′| Forn=1,…,|Gt∪Gt′/S| φn=∑nm=1I[k-1],Gt∪Gt′/S[m],其中Gt∪Gt′/S[m]表示剩余订单中的第n个订单,φ0=0;Endfor生成随机数γ∈(0,φ|Gt∪Gt′/S|]并判断其所处位置,若φn-1⩽γ⩽φn,则将剩余订单集合中对应位置的订单Gt∪Gt′/S[n]放入基因序列第k位,并将该订单添加至已选择集合S;Endfor 本文采用文献[16]的基于整数序规范(IOR)的变异和交叉算子进行种群个体进化迭代。其中变异操作是在当前种群中随机选择的个体a和b的基因进行差分运算,并按照缩放因子ρ调整差分值,再与目标个体c相结合而生成变异个体v。由于该方法产生的变异个体基因为实数,可利用IOR算子对变异个体v基因进行排序,根据基因顺序生成整数基因的变异个体。 交叉操作则是目标个体c以一定的概率与变异个体v交叉部分基因片段,从而生成新的试验个体u。为确保个体持续进化,试验个体u中的基因至少有一位是来自于变异个体v,剩余基因片段则根据交叉概率因子来确定是否进行交叉。交叉率越大,则变异个体所占试验个体的比例越大,反之则目标个体所占比例越大。为了提高算法效率,采用自适应交叉率δ,在种群进化前期交叉率较高,提高算法全局搜索能力;而在进化后期交叉率降低,从而提高算法局部搜索能力,加速收敛。 在进化个体适应度评价中,利用(16)式计算个体适应度。 π(u)=1/(C(u)+D(u)) (16) 其中,C(u)可利用目标函数(4)计算出个体u的总成本,D为等待时间约束破坏的惩罚成本,计算为: (17) 该式表示一旦某辆车中任意两个乘客的到达时间差大于Δtw,则设置D(u)为足够大的惩罚值,其中ϑ为极大惩罚因子。 在选择操作中,比较试验个体u与目标个体c的适应度,若π(u)>π(c),则选择试验个体u进入下一代,否则保留目标个体c。 为验证前瞻式匹配策略和改进DE算法的有效性和性能,本文提取了某在线拼车平台在成都双流国际机场8天内664个机场拼车订单,具体订单数据描述请见文献[17]。基于这些订单数据,利用Python语言搭建仿真实验平台,对本文提出的前瞻式匹配策略与实际中采用的两种匹配策略进行对比分析,同时对比测试改进DE算法与文献[15]和[16]中针对不同编码解码方式DE算法的性能。 实验利用真实订单数据,检验前瞻式匹配策略(PM)和实际中采用的固定匹配策略(FS)和实时触发策略(RT)的效果。后面两种基于规则的匹配策略的介绍,请参考文献[17]。实验采用PM、FS和RT三种策略,分别确定每个决策周期内待匹配的订单集合,并利用CPLEX软件求解模型PD获得最优的订单匹配和车辆路径规划方案。本文选取问题目标函数(4),乘客平均等待时间和车辆行驶路程作为评价指标。 首先,设置目标函数(4)中等待时间成本系数σ=0.1,对应的平台目标函数总成本如图3所示。其中,PM策略的总成本最低,其平均成本相对于FS和RT策略分别减少了17.52%和11.96%。其次,如图4所示,在乘客平均等待时间方面,PM策略具有较明显优势。乘客平均等待时间保持在大约5分钟左右,而FS策略和RT策略的等待时间平均为14.4和16.2分钟。较长的等待时间影响了乘客对拼车服务的体验,进而降低了乘客后续使用拼车服务的意愿。在车辆行驶路程方面,如图5所示,FS策略对应的车辆总路程最长,PM策略与RT策略的总路程相对接近。但平均看来PM策略的总路程仍然是最低,比FS和RT策略分别减少了10.26%和1.52%。 上述实验结果表明,尽管在大幅缩短乘客等待时间情况下,PM策略依然能够有效降低车辆行驶路程,其原因在于PM策略考虑了即将到达乘客的订单信息,因此能获得更优的方案。 本部分通过将改进DE算法与文献中提出的实数编码DE算法[15]和序数编码DE算法[16]进行数值算例对比测试。为此,按下面方式随机产生N=4,6,8,…,30不同订单数的算例。其中,订单i和订单j到达拼车点时间间隔服从Δti,j泊松分布P(λ=5个订单/30分钟);利用正态函数N(19.9,4.32)km随机生成机场到订单目的地的距离,利用N(7.3,4.52)km随机产生订单到参考点的距离,再根据欧几里得距离公式计算出订单i和订单j目的地之间的距离di,j。同时,设置订单i中乘客数量mi=1,2,3,4的概率分别0.4,0.3,0.2,0.1。上述参数的设置来源于文献[17]对实际订单数据的统计结果。针对上述每组参数,随机产生50个算例,并分别采用CPLEX优化软件,改进DE、实数编码DE和序数编码DE求解模型PD。由于模型PD为NP-难,设置CPLEX软件的计算时间上限为30分钟。当CPLEX在30分钟内无法搜索到最优解,则停止运算并输出当前最好下界。本文统一设置三个DE算法的种群规模为200,进化代数为200,差分缩放因子ρ=0.5。 上述算法求解数值算例的平均计算时间如图6所示。可以看出,随着订单数量的增加,CPLEX的计算时间呈显著增长,当订单数量N≥18时,CPLEX的求解时间超过30分钟。对于所有算例,三个DE算法的计算时间均在1分钟内。其中,采用实数和序数编码的两种DE算法求解速度最快,本文的改进DE算法相对较慢。原因是改进DE算法在初始种群产生和个体解码阶段采用了基于订单相似度的方法,增加了计算时间,但总体上改进DE算法仍可以满足实际运营过程中对响应速度的苛刻要求。 在解的质量方面,如表1所示,当订单数量较小时,三个启发式算法均能获得最优解,但随着订单数量的增加,实数编码和序数编码DE算法搜索到的解质量明显下降。在CPLEX所能求解到最优解的订单范围内(N≤16),改进DE算法与最优解的GAP值最高为0.55%。对于所有算例,改进DE算法平均GAP为14.68%,相对于实数编码和序数编码DE算法,改进幅度分别为53.62%和52.15%。原因主要是实数编码DE算法将整数范围优化问题的解空间扩大到了连续的实数范围,随着订单数量的增加,解空间呈指数级增长趋势,导致算法收敛效果较差;而序数编码DE算法的进化个体解码,车辆往往需要达到载重上限才会分配新的车辆,但本文的机场拼车问题中,把多位乘客指派到同辆网约车会增加乘客的等待时间。 表1 三个DE算法求解质量偏差对比 本节利用5.2节数值算例产生方法,进一步分析订单乘客数量和最晚等待时间对三种策略匹配效果的影响,并分析PM策略中等待时间成本系数的影响,为机场拼车服务的实际运营提供指导与借鉴。 首先,为了测试订单中不同乘客数对策略的影响,设置算例中总乘客数量M=40,50,…,160,并将M个乘客完全随机指派给40个订单,对于给定参数M产生30个算例。三种策略对应的车辆平均行驶路程和乘客平均等待时间如图7和8所示。 从图7可以发现,随着订单中乘客数量增加,拼车匹配的可能性逐渐降低,三种策略对应的车辆平均行驶里程也随之上升。特别是当M=160,即每个订单有4位乘客,由于车辆座位数限制,乘客无法实现拼车出行,车辆行驶距离最大。从图8可以发现,PM策略中乘客平均等待时间随着M的增加而减小,其余两种策略没有明显变化。特别地,当M=160时由于无法拼车匹配,PM和RT策略对应的乘客等待时间为0,而FS策略下乘客仍然需要等待较长时间。 此外,本节分析乘客最长等待时间Δtw=15, 20,…,60分钟对三种策略匹配效果的影响。对于FS策略,直接设置ΔT=Δtw。 由图9和10可以发现,随着Δtw增加,PM和RT策略可以在更长时间范围内匹配订单,因此对应的车辆平均行驶路程明显下降,但乘客平均等待时间上升。对于FS策略,乘客的等待时间略微有所上升,但车辆平均行驶路程无明显变化趋势。 此外,乘客等待时间成本是本文研究问题的主要特征,由于FS和RT策略中未考虑乘客等待时间影响,本文仅对PM匹配策略设置σ=0.01,0.1,0.5,1,随机生成30组算例进行测试,分析在匹配决策周期内乘客等待时间成本系数σ对PM匹配策略的影响。实验结果如图11和图12所示。 随着权重参数σ的不断增大,乘客的平均等待时间呈明显下降趋势,但相应的订单平均里程则会显著上升。因此在实际运营中,需要充分权衡平台服务水平(乘客等待时间)和车辆运营成本(行驶路程),有效提高平台运营水平。 综上,针对机场动态拼车问题,本文所提出的前瞻式匹配策略和改进DE算法能够保证在实际运营中平台对乘客随机到达的实时响应,并且相对于已有的两种匹配策略和文献中的DE算法,可获得更好的乘客匹配和车辆路径规划方案。 在线拼车作为共享出行的重要模式已在实践中蓬勃发展,但目前尚缺少相关运作策略与优化方法。本文针对机场在线拼车平台面临的顾客等待时间长和网约车行驶成本高的突出问题,提出了前瞻式动态匹配策略和对应的两阶段随机规划模型。为了满足实际运营中对模型求解时间的要求,提出了基于贝叶斯更新的近似最优确定性模型和求解网约车路径规划的改进DE算法。在DE算法中构建了考虑时空维度的订单相似度计算方法,并基于此设计出进化个体解码方式以及初始种群的产生方法,从而提高算法的求解质量。最后,本文通过对比测试验证了前瞻式匹配策略和改进DE算法的有效性和计算效率。本文研究成果不仅可以应用于机场等城市交通枢纽的在线拼车问题,而且对互联网环境下的快递、餐饮配送和新零售场景下的订单动态分配和配送路线规划也有借鉴价值。4.3 初始种群产生

4.4 变异和交叉
4.5 适应度评价及选择

5 仿真实验
5.1 匹配策略对比测试分析

5.2 改进DE算法性能对比测试


5.3 灵敏度分析


6 总结
