基于客户信用度的物流配送车辆路径问题研究
2022-09-13许茂增
王 勇, 范 举, 刘 永, 许茂增
(重庆交通大学 经济与管理学院,重庆 400074)
0 引言
随着物流业的快速发展,客户信用受到物流企业的日趋重视,信用作为市场经济的基石,对物流行业的发展尤为重要。近年来,在物流配送过程中,频繁出现的客户交易违约失信问题,已经给物流企业造成了一定程度的损失,然而,基于客户信用度的车辆路径问题研究可以实现物流配送企业的高效率运作,进而降低物流企业的运营成本。因此,研究基于客户信用度的物流配送车辆路径问题,有利于构建城市物流配送的客户服务信用体系,并有助于城市物流配送系统的可持续发展。国内外学者在基于客户信用度的物流配送车辆路径优化问题研究主要集中在基于客户需求属性和基于客户重要度的车辆路径问题两个方面。
在基于客户需求属性的车辆路径问题研究方面,Panchamgam等[1]考虑客户需求属性和服务优先级研究了人道主义救援路线设计的层次旅行商问题,并进行了服务效率和优先级之间的均衡研究。朱莉等[2]研究了考虑灾民需求属性和决策者异质性行为的多阶段灾后救援物资分配和应急路径优化问题,并与不考虑异质性行为的传统救援调度方案进行了对比分析研究。胡晓伟等[3]研究了突发公共卫生事件下城市应急医疗物资优化调度问题,并研究了应急医疗物资供给不足情况下需求差异对公平分配的影响。Huang等[4]在人道主义救援行动中,设计了包含受援者需求属性的绩效指标,并研究了效率、效能和公平对车辆路线访问顺序和救济物资分配的影响。李珍萍等[5]考虑客户需求服务时间窗和客户不同需求的服务顺序构建了一种混合整数规划模型,并应用联合优化遗传算法研究了带时间窗和服务顺序约束的车辆路径问题。符卓等[6]针对软时间窗的客户需求订单拆分的车辆路径问题构建了数学规划模型,提出了禁忌搜索算法进行求解。根据上述研究文献可以发现,在物流配送过程中考虑客户需求、服务时间窗和车辆容量限制等属性为基于客户信用度的车辆访问序列优化和车辆路径优化模型构建提供了研究切入。
在基于客户重要度的车辆路径问题研究方面,Ma等[7]通过考虑客户重要性和客户聚集密度研究确定了客户服务顺序,构建了危险品运输中多站点车辆路径问题的多目标优化模型,并提出了一种求解模型的混合遗传算法。Bai等[8]在异质车辆包裹配送问题中考虑客户的重要性和紧急程度进行了客户服务排序,构建了一种基于客户优先约束的异质车辆配送优化模型,并提出考虑任务分配的启发式算法进行求解。王勇等[9]基于客户重要度进行了聚类分析,将客户重要度与服务时间窗相结合构建了一种双层数学规划模型,并提出GA-TS混合算法研究了基于客户重要度的混合时间窗车辆路径问题。于江霞等[10]根据客户消费频次和消费金额对客户进行了重要性分类,构建了一种基于客户分类的即时配送路径优化模型,并设计了遗传算法进行模型求解。丁秋雷等[11]针对易逝品物流配送中出现的干扰事件影响问题提出了优先服务重要客户的策略,构建了一种多目标干扰管理模型,并应用改进的蚁群算法进行模型求解。由上述相关研究可知,当前基于客户重要度的车辆路径问题研究主要集中在考虑客户重要性和紧急性构建车辆路径优化模型,进而确定客户服务访问序列问题等方面,而结合客户信用度研究物流配送车辆路径问题还有待进一步深入。
因此,本文通过考虑客户信用度对物流配送路线的影响,研究在配送路线安排中将客户服务分为不同信用等级并结合服务时间窗进行合理的运输调度,构建了基于客户信用度的物流配送车辆路径优化模型,并在模型中引入客户信用度作为影响违反时间窗惩罚成本的参数。同时设计了一种GA-TS混合算法进行模型求解,进而研究了基于客户信用度的物流配送车辆路径问题。
1 客户信用度计算
针对部分外卖平台尝试通过外卖历史数据获得客户的信用等级,进而给予不同等级客户不同的服务权限,如等级高的客户购买同样的外卖产品可以获得更多的积分服务,且在繁忙时段可以优先享受平台派单服务等。不同的客户信用等级对应着不同的信用值范围,而不同的信用值范围对应不同的客户信用度。本文将客户在配送时间内取消订单、无故退换货、拒收货、被卖家投诉和恶意差评等看作客户交易违约。假设选取客户中的样本总数为n,第i(i≤n)个客户3年内在网上订购商品总数记为Ai,发生交易违约的次数记为Bi,则第i个客户的信用值Pi(其中Pi∈[0,1])可以通过式(1)计算:
(1)
本文将客户信用等级划分为9类进行研究,并将信用值划分为9个区间,每个信用值区间对应相应的信用度值,则客户i的信用度γi可以通过式(2)计算得到,其中,e表示客户信用等级总数,λi为客户信用等级分类数。客户信用等级评价如表1所示。
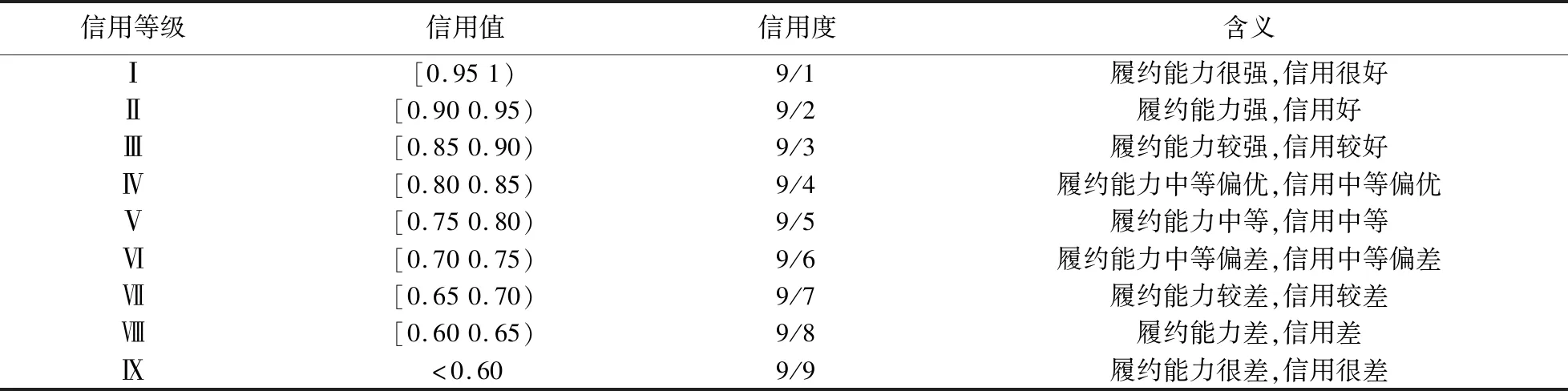
表1 客户信用等级评价表
(1)
2 模型建立
2.1 变量定义
相关变量定义如表2所示。

表2 变量定义
2.2 模型构建
本文以配送中心的物流配送总成本最小化为目标,结合客户信用等级划分表计算得到客户信用度,进而建立基于客户信用度的物流配送车辆路径优化模型如下:
minZ=TC1+TC2+PC
(3)
TC1:配送成本,配送车辆将商品送达客户的成本。
(4)
TC2:配送车辆的租赁成本。
(5)
PC:基于客户信用度的配送车辆违反服务时间窗的惩罚成本。
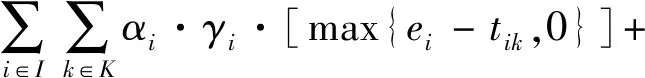
(6)
约束条件:
(19)
式(7)表示每一辆车从配送中心出发且最终返回配送中心;式(8)表示配送车辆将商品送达客户点后必须离开客户点;式(9)表示消除配送路线上的子回路;式(10)表示配送线路内需求商品的总量不超过车辆的最大装载量;式(11)表示所有配送客户的商品需求总量不超过配送中心的最大配送量;式(12)和(13)表示对于任一客户点,仅能有一辆车访问并离开;式(14)~(15)表示配送车辆离开和到达配送中心的时间必须在其服务时间窗内;式(16)表示配送过程的连续性;式(17)、(18)和(19)表示变量约束。
3 GA-TS混合算法研究
3.1 算法描述
本文设计了遗传-禁忌搜索(GA-TS)混合算法求解基于客户信用度的物流配送车辆路径优化模型。由于禁忌搜索算法对初始解具有较强的依赖性[12],为了提高算法的搜索能力,本算法设计过程先通过遗传算法进行全局搜索,提高种群规模的多样性,再应用禁忌搜索算法进行局部搜索,并采用精英保留策略返回遗传算法阶段进行循环迭代优化。该混合算法结合了遗传算法的全局搜索能力和禁忌搜索算法的局部搜索能力,进而拓展了算法的局部搜索空间和提高了算法的全局收敛性能。GA-TS混合算法操作流程图如图1所示。
3.2 算法检验
为了验证GA-TS混合算法的有效性,将GA-TS混合算法分别与混合遗传算法(HGA)[13]、禁忌搜索粒子群算法(TS-PSO)[14]和改进的蚁群优化算法(IACO)[15]进行比较。本文从Solomon数据集[16]选取了20组不同规模的随机测试数据,并将客户分为不同的信用等级分类方案进行研究。实验数据对应的数据集、客户数量、客户信用等级分类方案如表3所示。
通过表3的实验数据,分别从物流配送总成本、车辆使用数和算法运行时间三个方面比较四种算法的优化结果。四种算法的各项参数设置如下:GA-TS和HGA算法中的种群规模popsize=100,最大迭代次数maxgen=200,选择概率ps=0.9,交叉概率pc=0.9,变异概率pm=0.1;GA-TS和TS-PSO算法中禁忌搜索迭代次数tsin=40,禁忌表长度TL=28;TS-PSO算法中的惯性权重ω=0.9,学习因子c1=1.2,c2=1.4;IACO算法中的信息素权重α=1,启发因子β=2,信息素挥发系数ρ=0.5。将每种算法分别运行20次,提取20次计算过程的物流配送总成本最优解以及其对应的车辆使用数和算法运行时间,如表4所示。
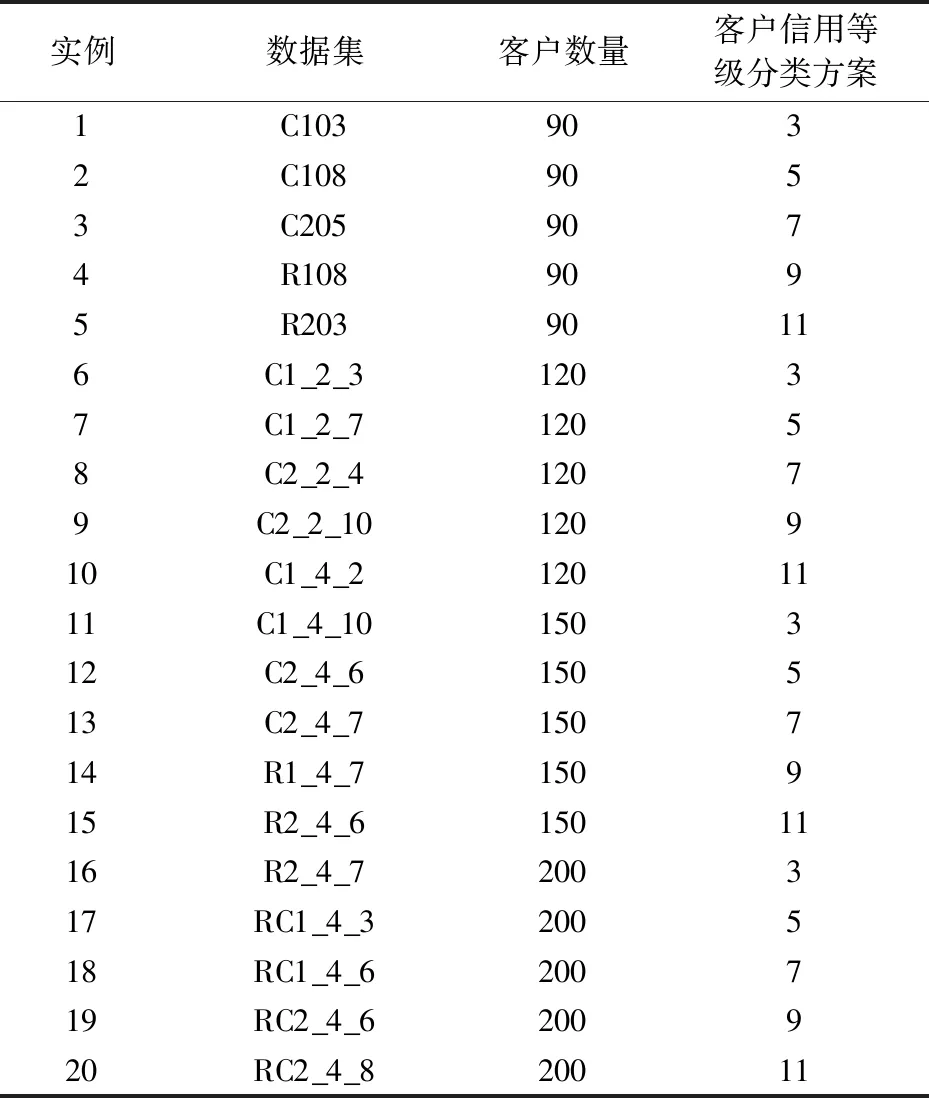
表3 数据集特征
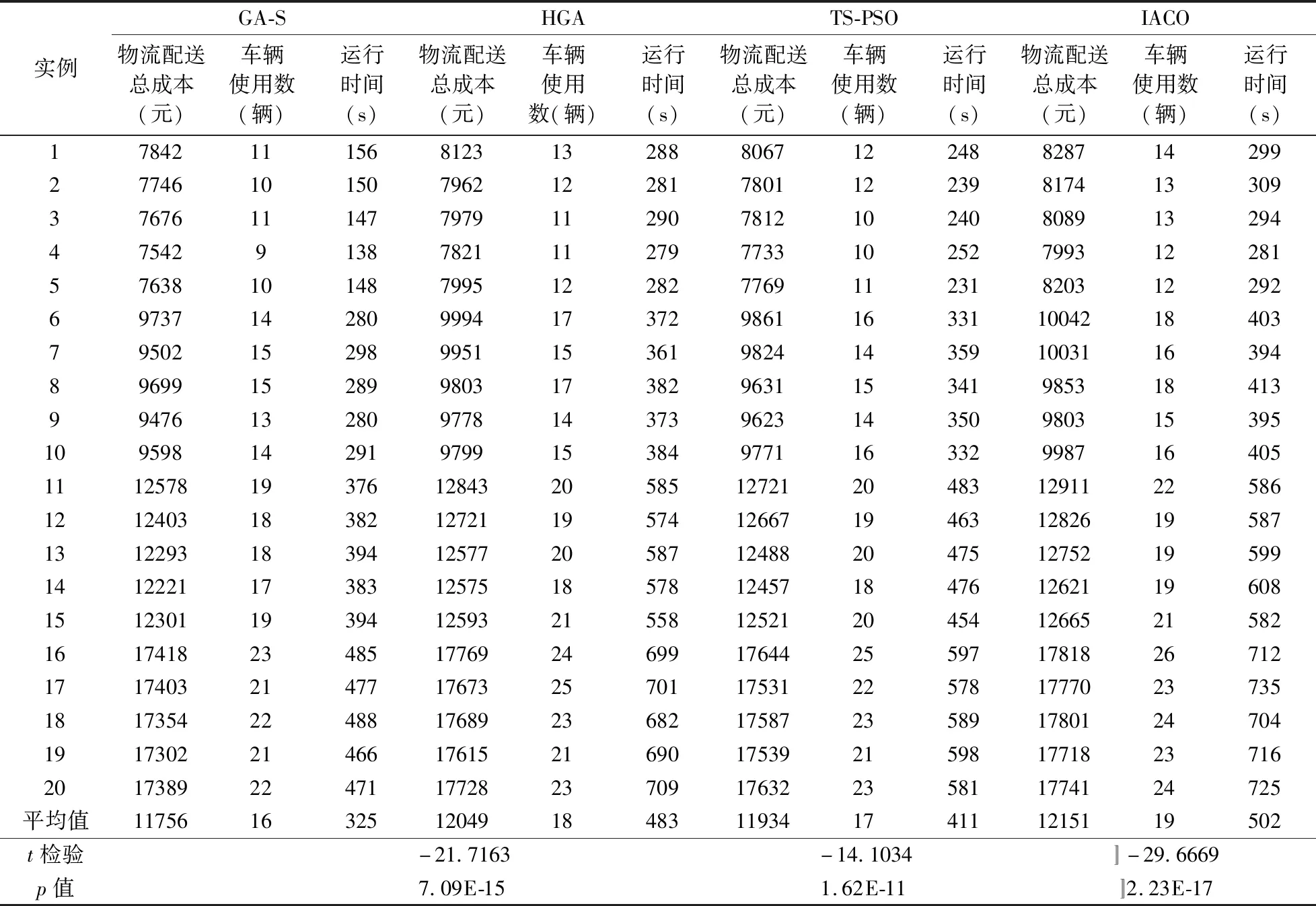
表4 不同算法优化结果的比较
由表4可知,其他三种算法相对于GA-TS混合算法求解的物流配送总成本对应的t检验值和p值具有明显差异性。GA-TS混合算法在配送总成本均优于HGA、TS-PSO和IACO算法,GA-TS混合算法的配送总成本平均值为11756元,而其他三种算法分别为12049元、11934元和12151元;四种算法求解的平均车辆使用数分别为16辆,18辆,17辆和19辆;此外,GA-TS混合算法求解20组数据的平均运行时间均优于其他3种算法。因此,本文所提的GA-TS混合算法相对于其他三种算法具有较好的稳定性和可靠性。
4 算例分析
4.1 案例相关数据
本文在重庆市选取了由一个配送中心(DC)和200个客户点(D1,D2,……,D200)组成的实际外卖物流配送网络作为研究对象,相应的地理位置分布情况如图2所示。
在现有文献[9,13,16]和多次计算实验的基础上,相关参数设置如下:车辆最大装载量Qk=20,百公里油耗量fk=2.89,汽油价格ρc=6.09,车辆租赁成本σk=50,种群规模pepsize=100,最大迭代次数maxgen=200,选择、交叉和变异概率ps=0.9,pc=0.9,pm=0.1,禁忌搜索迭代次数tsin=40,禁忌表长度TL=28。
4.2 结果及分析
应用GA-TS混合算法求解基于客户信用度的物流配送车辆路径,计算得到的优化方案如表5所示。
由表5可知,以考虑物流配送总成本最小化为目标的基于客户信用度的外卖物流配送优化方案中,配送中心需要派遣27辆车对200个客户点进行配送服务。结合前期调研获取的客户点配送线路(优化前),通过本文构建的模型和算法计算获得客户点配送线路(优化后),进而得到基于客户信用度的外卖物流配送成本。基于客户信用度的外卖物流配送优化前后的对比结果如表6所示。

表5 基于客户信用度的外卖物流配送优化方案
从表6可知,相比优化前的配送方案,考虑客户信用度的优化方案有效降低了物流配送总成本。其中,配送成本、车辆租赁成本和基于客户信用度的违反时间窗惩罚成本分别降低了49%、18%和70%,车辆使用数由33辆减少到27辆,违反时间窗的客户点数由24个减少到9个。因此,在物流配送车辆路径优化中结合服务时间窗将客户服务划分为不同信用等级进行配送,可以有效降低物流配送成本,进而提高城市物流配送效率。

表6 基于客户信用度的外卖物流配送优化前后结果对比
4.3 分析与讨论
基于客户信用度的物流配送车辆路径问题是以物流配送总成本为优化目标,在优化过程中基于客户信用度的违反时间窗惩罚成本是物流配送总成本的重要组成部分。为了进一步研究客户信用度高低对物流配送总成本的影响,设定车辆路径优化过程中,优先服务信用度高的客户点,对于信用度相同的客户结合客户服务时间窗进行车辆路径优化,进而计算得到配送成本,车辆租赁成本,违反时间窗的客户点数,车辆使用数和物流配送总成本。客户配送服务方案调整前后优化结果对比如表7所示。
由表7可知,优先服务信用度高的客户方案调整后,物流配送总成本增加了6%,车辆使用数增加了3辆,违反时间窗的客户点数增加了5个,而由于调整了客户服务策略(即优先服务信用度高的客户),使得基于客户信用度的违反时间窗惩罚成本反而减少。因此,结合客户服务时间窗和客户信用度进行物流配送车辆调度有利于进行有效的客户配送服务和进一步降低系统的物流配送总成本。

表7 优先服务信用度高的客户方案调整前后结果对比
4.4 敏感度分析
本文的敏感度分析包括客户不同信用等级变化的敏感度分析和客户信用等级分类方案的敏感度分析。客户不同信用等级变化的敏感度分析是将客户的不同信用等级依次全部统一调整为Ⅰ级、Ⅱ级、Ⅲ级、Ⅳ级、Ⅴ级、Ⅵ级、Ⅶ级、Ⅷ级和Ⅸ级,计算每次调整后的物流配送总成本、违反时间窗的客户点数和车辆使用数,计算结果如图3所示。
由图3可知,当所有客户的信用等级依次从Ⅰ级改变至Ⅸ级时,物流配送总成本、违反时间窗的客户点数和车辆使用数均会随之改变。当将所有信用等级调整为Ⅰ级,II级和Ⅸ级后进行配送服务时,物流配送总成本会增加。由于对信用等级全为Ⅰ和II级的客户进行配送服务时,虽然违反时间窗的客户点数较少,但单位时间的惩罚成本系数大,也将产生较高的惩罚成本,进而导致物流配送总成本增加;对信用等级为Ⅸ级的客户进行配送服务时,虽然单位时间的惩罚成本系数小,但违反时间窗的客户点数较多,产生的惩罚成本也随之增加,进而导致物流配送总成本增加。而将所有信用等级调整为Ⅳ级后的客户进行配送服务时,物流配送总成本和车辆使用数均最小。
客户信用等级分类方案的敏感度分析主要是研究客户信用等级不同分类模式下应用本文构建的模型和提出的混合算法计算比较物流配送总成本、违反时间窗的客户点数和车辆使用数的变化。将客户信用等级分别分为2~12个分类方案,进行计算结果比较,如图4所示。随着客户信用等级分类方案的增加,物流配送总成本、违反时间窗的客户点数和车辆使用数均会随之改变,当客户信用等级分类为7、8和9时,对应的车辆使用数相同,但客户信用等级分类为9时,对应的物流配送总成本和违反时间窗的客户点数均优于客户信用等级分类为7和8时的对应方案;当客户信用等级分类为9和10时,对应的违反时间窗的客户点数相同,但客户信用等级分类为9时对应的物流配送总成本和车辆使用数均优于客户信用等级分类为10时的对应方案。本文的优化目标是基于客户信用度的物流配送总成本最小,因此,客户信用等级分类结果为9时对应的物流配送方案最佳,同时也表明对客户信用等级进行合理分类,可以有效降低物流配送总成本,减少违反时间窗的客户点数和车辆使用数。
5 结论
本文研究了基于客户信用度的物流配送车辆路径优化问题,将客户分为不同信用等级并结合服务时间窗进行合理的配送线路调度,通过引入客户信用度作为影响违反时间窗惩罚成本的参数,建立包含物流配送车辆的运输成本、租赁成本以及基于客户信用度的惩罚成本的物流配送总成本最小的优化模型,并设计了GA-TS混合算法进行模型求解,该混合算法通过有效利用GA的全局搜索能力和TS的局部搜索能力拓展了算法的局部搜索空间和提高了算法的全局收敛性能。将GA-TS混合算法与HGA算法、TS-PSO算法和IACO算法的求解结果进行对比分析,结果表明本研究提出的GA-TS混合算法优于其他算法。
本文通过基于客户信用度的模型求解对物流配送路线进行了优化设计,并以重庆市某外卖物流配送网络为例,验证了模型和算法的有效性。计算结果表明,优化后基于客户信用度的配送方案使物流配送总成本、违反时间窗的客户点数和车辆使用数分别减少了38%、63%和13%。此外,客户不同信用等级变化和客户信用等级分类方案的敏感度分析表明:客户信用等级全部调整为Ⅳ级时,物流配送总成本最小;客户信用等级分类方案为9时,对应的配送方案最优。本文为物流配送车辆路径优化问题提供了新的研究思路,且具有较强的应用价值。
