运用小学数学解决问题一题多变培养学生思维

◎陈 宁

(福州市鼓山新区小学，福建 福州 350011)

一、借“一维”变式，从“简单处”提升学生的能力

(一)解决问题一题多变从简单入手，提高学生的审题能力

虽然是数学学科，出于对学生综合能力的培养和提升，同样重视对学生阅读能力和提取信息能力的考查.当今数学解决问题多是大量情境文字，需要学生花时间取或舍信息.在测试时间有限及心理因素等作用下，人会本能地搜索或选择自己大脑中最熟悉或最浅显易懂的记忆存储(定式思维)，甚至因为恐惧而规避审题.审题能力是学生对信息提炼、分析、处理、整合、加工和运用的能力.解决问题一题多变有利于培养学生的审题意识和能力，能够引导学生关注中心信息，并将繁杂信息进行取舍、整合，这也是一种化难为易的能力.

“天下难事，必作于易”.因此，在一题多变时，教师宜从简单入手，让学生树立应对一题多变的信心.例如，在教学人教版六年级数学上册中分数的解决问题时，为了让学生感悟到一题多变对于审题的意义，我做了以下设计:

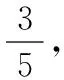
解分数应用题的关键在于找“1”，判断“1”是已知还是未知，进而选择方法予以解决.然而，通过日常教学实践，我们发现学生由于没有对“1”的作用进行深刻领悟、为避免麻烦的心理或对“1”的轻视等原因，经常会凭感觉解决问题，没有认真审题或分析“1”，因此，教师应针对学生的错点、漏点、薄弱点进行细微的“变”，具体如下.

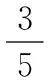
通过教师示范“变”，大部分学生会条件反射地关注变式题和例题信息的不同之处，从根源上体会例题与变式题的不同之处对解决问题产生的影响，感受解决问题一题多变，从“变”中体验细节的重要性，从“变”中体会审题对分析问题、解决问题的“首因”作用，增强学生的目标性审题意识，培养学生思维的严谨性.

(二)利用动态评价，树立“变”的信心，激发学生“变”的积极性

有焦点，必有盲点!在数学解决问题一题多变的教学中，教师应不吝啬对学生的鼓励和认可，动态、智慧地评价，激发学生关注更多的“盲点”，引领学生创造性地“变”.例如，“你的‘变’在提醒同学们关注信息的同时别忘了关注问题”“你的改变虽然只是区区两个大字,但影响重大,可谓失之毫厘，谬以千里！”师生、生生之间的或及时、或延时的评价，会优化课堂生态，“暖化”学生内心，增加学生的心理能量……因简单的“变”，结不简单的“果”！教师可以调动学生主动创新“变”的积极性，催生出“题链”.

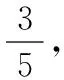
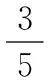
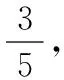
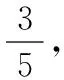
能力培养是由简到难、由浅入深的，让学生在接受新知识的同时形成数学基本技能，促成数学抽象、逻辑推理、直观想象等数学核心素养的养成.教师应激发学生从细微处观察、辨析异同，促进学生在解决问题中主动探索、严谨审题；鼓励学生从“一维”视角审视题目，并进行个性的“变”.学生自主参与条件的“变”或问题的“变”能改变一成不变的题目模式，因此，教师应培养学生的创新意识和创新能力，预防思维定式，规避题海战术，强化学生解决数学问题的敏锐性，培养学生养成关注细节的良好品质.

二、巧用解决问题一题多变，探寻变式题的内在本质，提升学生的思维品质

(一)用“二维眼光”探“一维题目”，通过拆解、对比、辨析提升学生思维的系统性

数学解决问题常常是披着不同的生活情境、各种数学表象的外套，但是本质上是相同、相通或类似的.因此，教师可以引导学生在一系列的数学问题中进行思考，在情境中追寻和辨析其异同，主动探寻题组间的内在本质，提升学生辨识“题组”的能力，拓展学生解决问题策略的途径，提高学生分析、解决问题的能力.

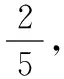
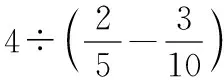
变式1:小华有46张邮票，小廖有38张邮票，小廖给小华几张邮票后，小华与小廖的邮票数之比是9∶5?

变式2:A、B两个车间原有人数的比是3∶2，从A车间调48人到B车间后,A、B两个车间的人数比是2∶3，原来两个车间各几人?

题组间从表面上看不相关，因此，教师可以引导学生将例题和变式题进行对比、辨析，使学生经过交叉、拆解后发现:变式1中的小华、小廖的邮票总数量以及变式2中的A、B两个车间原有的总人数相当于例题中的杨树、柏树的总棵数.例题是把柏树换成杨树，变式1是将小廖的邮票给小华，变式2是A车间的人调去B车间.虽然题组间的情境看似相差十万八千里，但是通过拆解、多角度探寻，我们不难发现看似不同的表象后面，原来只是换汤不换药，脱下各色的外套后，里子是一致的.“变化中找不变”的解题方法、解决问题的策略等均是相似的.

(二)用“二维眼光”探“一维题目”，实现知识的融会贯通，增强学生思维的深刻性

本是同根生，却各有不同.知识是静态的，思维是动态的；考点是固定的，形式变化却是无穷的.教师应在“变”中引导学生建立不同解决问题的线性、面性、立体化的联系，以便学生在不同的数学问题中自由穿梭，实现知识的融会贯通，增强学生思维的深刻性.

3人教版六年级数学上册“圆的面积”一课后有一道习题:

把一个圆形纸片沿半径平均分成若干份，拼成一个近似的长方形.如果长方形的长比宽多8.56 cm，原来圆形纸片的周长是( )cm.

学生运用数形结合思想后明白:近似长方形的长边相当于原来圆周长的一半，宽边相当于原来圆的半径，得出一个方程-=8.56，用方程的思想求出半径，推进问题的解决.为了让学生实现对知识的融会贯通，我精心准备了变式:

如图1所示，已知圆的周长是6.28 cm，圆的面积与长方形的面积相等，长方形的长是( )cm.

A.3.14 B.6.28 C.12.56

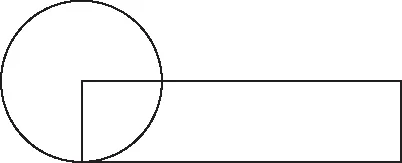
图1

在独立完成变式题时，大多数学生运用常规思维分析、解决问题，此时，教师没有打断学生，而是引导学生从本质上追寻、探索变式题目与例题之间的内在联系，使学生发现例题与变式题都是长方形的宽边相当于一个圆的半径，长方形的面积=一个圆的面积.虽然表现形式不同，本质却是相同的，因此，教师可以引导学生将变式题融入例题中，实现学生对知识的融会贯通的目的.

(三)用“二维眼光”探“一维题目”，认识、领悟数学模型“变化”中“不变”的本质，助力学生思维的创新性

虽然变化是唯一的不变，但是在大千世界这多元的变化中，也冥冥隐藏着“不变”的因素.在数学课堂上，教师应该智慧、创造性地利用、挖掘教材中例题的价值，建立在“一维”变化的基础上引导学生沉下心来仔细观察、深度思考，促使学生努力探寻变化背后隐藏的可能不变的成分，进而放手让学生在认识、领悟数学模型“变化”中“不变”的数学本质的基础上，给予学生充足的创造时间，并相信学生的创造性，鼓励学生多样化、个性化、创造性的“一题多变”，使他们能在数学解决问题一题多变中取得各自的收获，同时提升他们思维的创新性.

如图2所示，对于人教版六年级数学上册关于外方内圆与内方外圆的阴影部分(圆与正方形之间的部分)面积的探索，

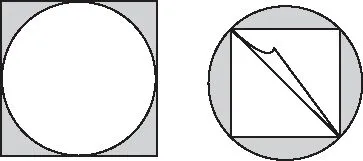
图2

学生了解了虽然数学解决问题的外在图形(表现形式)不同，但是求阴影部分面积的策略方法是一致的，就是大面积-小面积=阴影部分的面积.下面以方中圆为例，在学生推导得出方中圆的阴影部分面积=0.86后，教师可以充分挖掘教材中例题“变”的价值，设置一题多变的新题,如图3、图4所示.

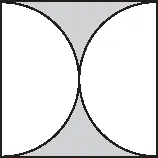
图3

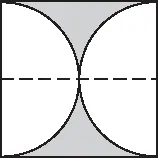
图4

面对既陌生又熟悉的研究对象，学生的好奇心和研究心被调动起来，学生积极主动地认真观察变式后的图，并进行独立思考和解答.在充分探究的基础上，学生总结出特别可喜的两点：一是这幅图在本质上是外方内圆，是将一个圆分割成两个半圆.二是方中圆的阴影部分其实是一个近似的三角形，而变式的这道题经过添加辅助线，也有近似三角形，与方中圆的阴影部分一致.所有的变式创新都需要建立在认清本质的基础上，数学解决问题一题多变必然会使学生分辨出同一事物下的不同之处，集思广益，丰富课堂内涵，为创新积蓄必需的力量.教师应抓住“变”的时机，在课堂上给予学生一题多变的时间，让所有学生在认识、领悟数学模型“变化”中“不变”的本质的基础上以母题为版本进行一题多变.图5是截取部分学生当堂一题多变的设计例子.

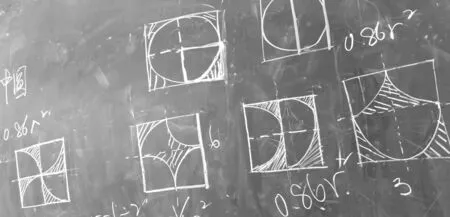
图5

同时，教师可以引导学生辨析和反思，呈现出学生主动创造、思辨的充满生机活力的课堂.虽然课堂时间是有限的，但一题多变的魅力和价值是无限的.教师可以将一题多变延伸到学生的课后，为学生创造更多的“变式”留足空间，最大限度地激活学生的思维潜能，助力学生思维的创新性.

教师可以借助小学数学解决问题中的一题多变，引导学生从横向、纵向等多个角度主动探索与对比变式，用“二维”眼光看“一维变式”题目.学生经历了辨析“变”的过程，能够培养自身的逻辑思维能力和加深自身对教学的深刻理解.教师可以引导学生透过现象看本质，总结如何用数学知识解决问题的特征，多题归一，增强学生思维的深刻性，提高学生分析问题和解决问题的综合能力.

三、妙用“实际生活”促发“一题多变”，建构数学模型，培养学生形成立体化思维

知识可以传授，方法可以渗透，唯有智慧只能靠学生自己亲历累积.数学问题的“变”不都是数学层面的“变”，数学知识与生活密切联系，教师要善于抓住资源，个性化地使用教材，让学生感受到数学解决问题也因实际生活而产生“变”，引导学生用生活视野看待数学，用数学思维思考生活，亲历“变”的过程.

例如“植树问题”，我结合文本设计了相对简单的数学解答问题：一条大约是长30米的细长道路，在这条细长道路的一旁每隔5米就要连续种一棵落叶树，要栽多少棵树?让学生独立思考，鼓励学生求出答案.于是，教师可以结合实际生活进行一些改变，如在生活中，如果路的一端或两端都要建建筑物，就存在一端不能栽树或两端都不能栽树的情况.这样一来，教师通过巧妙地联系实际生活造就了数学解决问题的“变”，使学生能感受到数学和生活之间的紧密联系，使学生能建构出两端都可以栽树、一端不能栽树、两端都不能栽树的情况下是否有植树问题的模型.教师结合生活多变的情境，巧妙地促成了学生形成多变、全面的思维.

学生亲历解决问题的“变”，在建构模型后,教师顺势而“变”.例如，“一个大钟7时敲7下，9秒钟就能敲完.一个大钟10时敲10下，敲完需要多长时间？”“一根100米长的钢管，截成每20米一段的小段，一共要截多少次？”等问题.教师引发学生联系植树问题模型展开思辨，不仅使学生解决了数学问题，还将数学解决问题最大限度地投射到学生的思维深处，使他们实现对知识的螺旋式再认识.

创新是一个民族的灵魂，是人类智慧的结晶，数学解决问题一题多变是培养小学生创新能力的有效途径之一.学生通过亲历和感受“变”、参与“变”、辨析“变”、结合“变”建构模型等学习活动，以“变”为媒介，既掌握了数学知识，又积累了学习经验和方法，同时形成了能力，提升了数学素养，培养了思维品质、实践能力和创新能力.“合抱之木，生于毫末；九层之台，起于累土”.学生在努力积累“一题多变”经验的过程中学会了用数学的视角观察世界，用数学的思维想象世界，用数学语言表达世界，用个性化的思想感动世界，用丰富的内心影响世界，可谓一举多得.