数学文化融入高中数学教学的实践研究——蒙日圆问题引发的思考

◎赵思博

(甘肃省民乐县第一中学，甘肃 张掖 734500)

一、引 言

高中数学教材中渗透的数学文化素材既增强了教材的可读性，也增加了学生对数学文化的认同感.数学文化融入课堂教学中对提高学生的思想境界和文化修养，以及落实核心素养有重要作用，是体现数学育人功能的有效方式.下面从蒙日圆问题教学过程中引发一些思考并进行探索交流，溯本归源，循序渐进，实现课堂教学的“深度学习”.

二、创设情境，启发思考

初中阶段，对圆及圆的有关性质的认识和学习侧重于几何直观和推理论证，要求学生能利用平面几何的知识论证圆中的有关问题.高中阶段，注重坐标法思想内涵的理解和应用，通过直角坐标系用代数方法来研究圆的方程及有关性质，代数运算与几何直观深度融合，使学生对圆的认识更为完善.数学家加斯帕尔·蒙日的画法几何学中有一个有趣的结论：椭圆的任意两条互相垂直的切线的交点都在同一个圆上，它的圆心是椭圆中心，半径等于椭圆长半轴和短半轴平方和的算术平方根，这个圆叫蒙日圆.

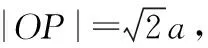
研究性问题：若将圆压缩为椭圆，过椭圆外一点作椭圆的两条互相垂直的切线，则动点的轨迹又是什么曲线？对于这个问题教师可借助信息技术让学生有一个直观认识，通过几何画板的演示，观察动点运动过程中留下的痕迹，发现是一个圆.这个圆的圆心在坐标原点，那么这个圆的半径是什么呢？

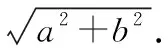
三、证明结论，提升逻辑推理素养

关于蒙日圆问题的证明，对培养学生的直观想象、逻辑推理和数学运算素养是很好的载体.解析几何的教学要把重点放在对坐标法的理解和应用上，加大用坐标法思想分析问题的力度.关于定理的证明，我在教学中还是采用了代数方法.我在实际教学中发现：学生的着眼点往往放在互相垂直的两条切线上，很自然地想到的是直线的斜率互为负倒数，用斜截式方程设出两条切线方程，然后把直线方程与椭圆方程联立，而这也是解决直线与圆锥曲线位置关系问题的套路化做法.此问题是轨迹问题中的“交轨法”应用的典型问题，学生会把两条切线方程联立后求动点的坐标，其结果中是含有参数的，而消参化简则成为一个不易突破的难点.

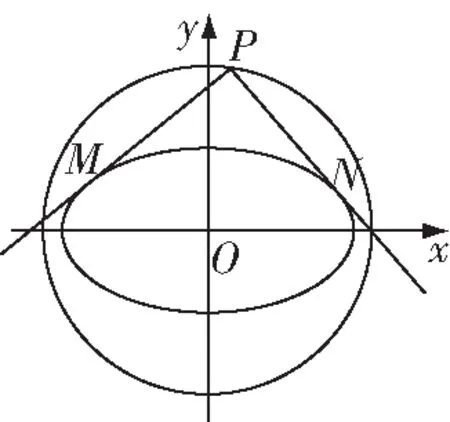
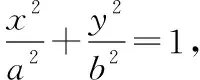
证明：若两条切线分别平行于轴和轴，则交点(±,±).

易证点在圆+=+上.

若两条切线斜率均存在，可设两条切线方程如下：

:=+，

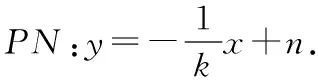
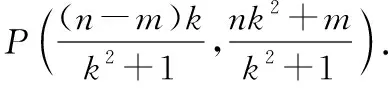
则点距离椭圆中心的距离的平方为：

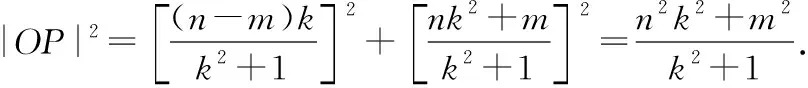
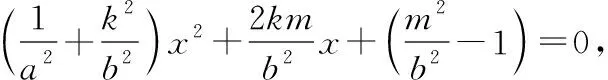
(+)+2+(-)=0.

由于直线与椭圆有唯一公共点，

则=4-(4+4)(-)=0，

化简，得=+.

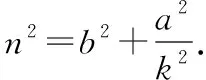
把,代入，就得到：

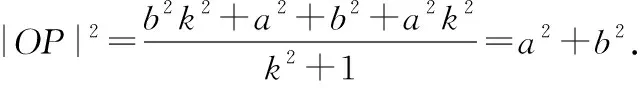
四、基于逻辑推理，推导椭圆的切线方程及切点弦方程

在数学教学中，教师要基于基础知识和基本方法，通过问题解决的过程和方式，加强数学思想的渗透和解题方法的提炼，让学生的数学思维和数学素养得到发展和提高.在学习中，教师既要培养学生善于观察、思考、探究的良好习惯，又要引导学生注重知识发生发展的逻辑合理性，以“问题串”教学设计，创设逻辑连贯、针对性强的探究活动，启发思考，使学生的学习走向深刻.通过以上证明过程，可展开如下探究.

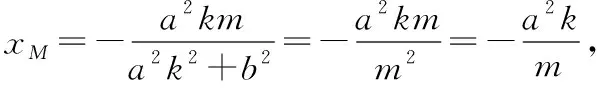
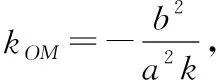
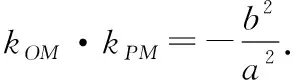
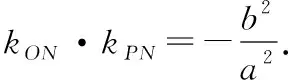
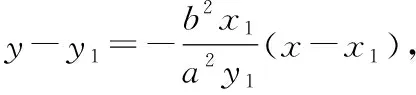
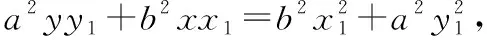
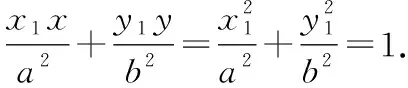
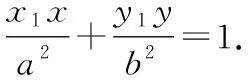
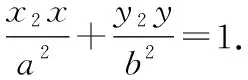
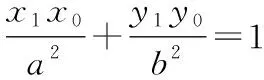
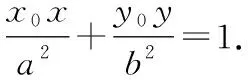
五、切线方程推导的极限法

教学活动的创设以学习对象为主体，要体现数学学习的实效性和思想性，经过观察、猜想、推理、论证、总结，认识数学问题的起源，理解数学问题的本质，探索解决问题的方法，归纳对教学有发展意义的数学结论.教师要引导学生开展体验学习、建构学习、有逻辑的系统学习，促进数学知识的系统化，增强学生对数学方法的深刻理解，强化其应用数学的意识，逐步培养数学学科素养，使学生的理性思维逐步走向成熟.

思考和探究永不停止，学生的想法往往出乎意料.对于椭圆的切线方程的探索，有的学生提出如下做法：设(,)，(,)，

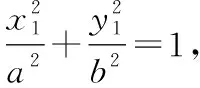
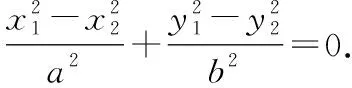
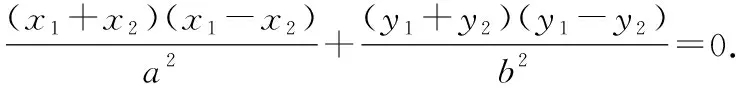
设椭圆的弦的中点为(,)，

则有+=2,+=2.

当≠时，

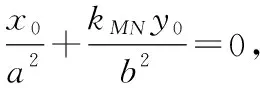
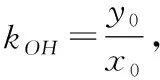
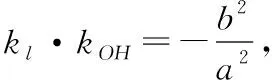
极限法推导椭圆的切线方程是极妙的做法，这是学生灵活运用数学思想方法解决问题的体现.

六、蒙日圆定理的证明2

证明：若两条切线的斜率都存在，设(,),过点的切线方程为-=(-).

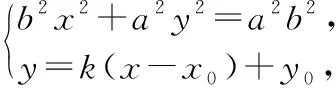
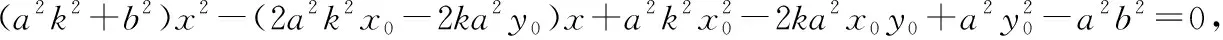
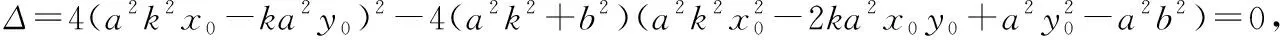
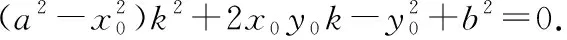
由于,是该方程的两个解，

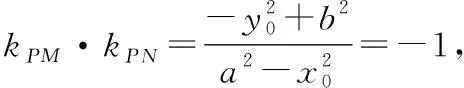
若两条切线分别平行于轴和轴，则交点的坐标为(±,±)，显然满足圆+=+.

证明2是先设出了动点的坐标(,)，把过点的切线统一表示为-=(-)，依据直线与椭圆相切则=0，得到关于的一元二次方程，而两条切线的斜率,为方程的两根，且乘积为-1，直接推出了动点的轨迹方程.

七、变式追问，设置问题串，促进深度理解

教学中，教师基于知识生成和思维发展推进深度教学，对如何观察发现圆锥曲线的几何特征，如何构建有效研究路径，如何证明圆锥曲线的几何性质，如何用坐标法研究几何问题都要加强指导，挖掘创新点，拓宽问题辐射面，突出数学素材的应用价值和教育价值，以提高课堂教学的思想性和实用性.通过上述的证明，教师可引导学生进一步展开探究.

(1)我们看到该问题中两条切线的斜率乘积实际上是一个常数-1，那么这个常数取其他值时，动点的轨迹又是什么曲线呢？

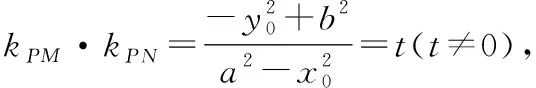
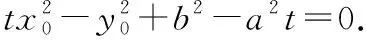
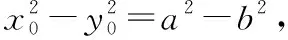
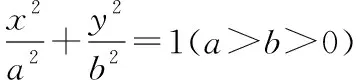
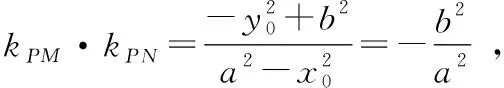
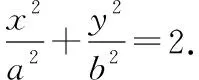
(3)如果考虑两条切线的斜率之和为一个常数，那么动点的轨迹又是什么曲线呢？

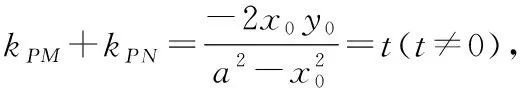
八、延伸—拓展—推广，实现深度教学

如果把椭圆变为抛物线，能否用同样的方法研究两条切线的交点的轨迹？

过抛物线=2外一点作抛物线的两条切线,，使得⊥，则动点的轨迹是什么曲线？

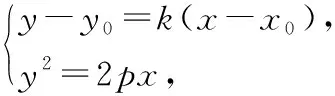
又直线与抛物线相切，则=0，

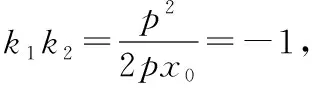
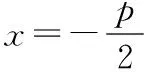
该问题中两条切线的斜率乘积是一个常数-1，那么这个常数取其他值时，动点的轨迹又是什么曲线呢？

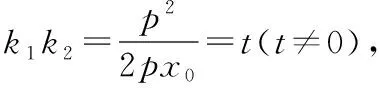
如果考虑两条切线的斜率之和为一个常数，那么动点的轨迹又是什么曲线呢？

显然，为0时，动点在轴的负半轴上.

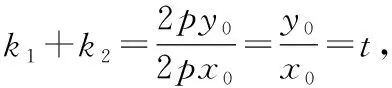
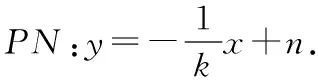
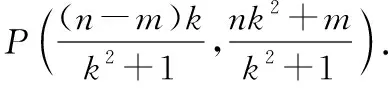
现将:=+代入=2，消，化简，得：

+(2-2)+=0，

由于与抛物线有唯一公共点，则=4-8+4-4=0，

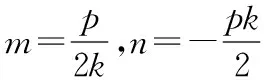
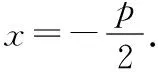
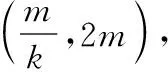
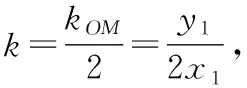
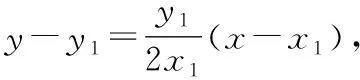
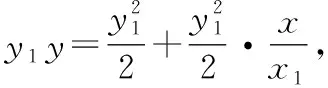
类似地，过点()的切线方程为=(+).

又因为这两条切线都过点(,)，则有=(+)，=(+)，

故经过,两点的切点弦方程应为=(+)，此方程表示过定点(-,0)的直线.

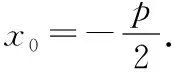
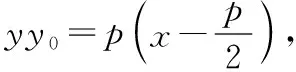
九、引申和探索——直线过定点问题

在直线=上任取一点(,)，过该点作抛物线的两条切线,，切点分别为,,切点弦过定点.

过点(,)的切线方程为=(+)，过点(,)的切线方程为=(+),又因为两条切线都过(,)，则有=(+)，=(+)，切点弦的方程为=(+)，该直线过定点(-,0).

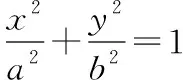
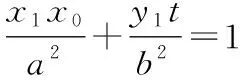
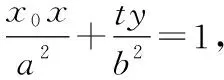
十、结束语

数学教学基于数学基础知识的积累，注重数学学习习惯和规范的养成，更重要的是渗透数学思想方法，凝练数学学科素养，发展关键能力.数学文化素材在教材中的展现让学生深入地了解了数学知识源远流长.在课堂教学中融入数学文化素材对学生在转变数学观念、发扬数学精神、培养数学素养方面具有重要作用和价值.教学中，只有教师打开自己的数学视野才能让数学文化融入更为普遍、更为一般的数学课堂里.