新高考三角函数与导数“联姻”试题教学策略研究

◎吴依妹

(福建省闽侯县第一中学，福建 福州 350100)

一、引 言

我们可以从今年“八省联考”中的选择题12题与压轴导数大题看出，近年来，无论是地方大考，还是高考，都出现了三角函数与导数结合的“联姻”题型.它是试卷中的常客，甚至是重头戏，成为最具区分度的亮丽风景.这种题型命制不但没有成为桎梏，反而常考常新，丰富了教学素材.解决这类问题，除了应用三角函数的基本性质和运算以外，还要结合导数运算与综合应用，这是教和学的一大难题，对教师培养学生综合能力教学策略研究提出很高要求.

二、函数与导数的知识地位

高中阶段函数知识至关重要.我们利用函数知识可以解决很多生活中的问题.同时函数知识和其他知识具有一定的关联性，例如，函数和不等式、函数和平面几何等都有关联，学好函数有利于学好其他数学知识.在初中阶段，学生就开始接触简单函数，如一次函数、反比例函数等.学生升入高中后，开始接触更多更为复杂的函数，包括集合、三角函数、指数函数、对数函数等.学生在高中学习的函数，在大学中会被进一步深化，可以说高中函数知识是高等数学学习的基础.也就是说，在高中阶段我们学习好函数有助于我们对大学数学的学习.在高中，函数知识所占百分比较大，是高中学习的主要内容.学生如果想要提高数学成绩，就应该充分掌握函数知识.

导数对于高中生而言，属于初次接触，具有一定的难度.导数和函数息息相关，我们通过导数的学习可以解决函数的极值问题等.此外，导数和微积分有着紧密的联系，是学习微积分的基础.而微积分是大学数学的重要内容，所以说学好导数也可以为大学数学学习做好铺垫.同时，导数知识对物理学习有一定的促进作用，所以，导数知识的学习也极为重要.综合近几年高考来看，函数和导数有融合考查的趋势，因此教师在教学中应该深入分析函数和导数，重视对联合题型的讲解，以此来提高学生的数学成绩.

三、函数基本性质类问题策略研究

函数基本性质类问题主要包含单调性问题、奇偶性问题、对称性问题，此类问题是解决导数与三角函数“联姻”问题的基石.

(一)单调性问题

1.试题分析：这类题目常常涉及已知三角函数在某个区间上的单调性，求函数中参数的取值范围.

2.解题策略：我们常常可以利用导数与单调性之间的关系求解.若()在(,)上单调递增，则′()≥0恒成立，若()在(,)上单调递减，则′()≤0恒成立.

1(2018 年全国Ⅱ卷第10题)若()=cos-sin在[-,]上是减函数,则的最大值是( ).

此题运用三角函数的图像，结合区间上导函数′()≤0恒成立解决.

导函数是三角函数，图像的准确定位是关键，我们可以从图像中分析原函数的单调性.教师在教学时应注重引导学生进行“导数与三角函数”结合研究，培养其对“联姻”问题的综合分析能力.

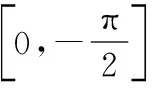
此题运用分离参数构造新的三角函数求最值来解决.

3.教学小结：解题时，从求导出发，利用单调性，结合三角函数图像，求出参数范围.

(二)奇偶性问题

1.试题分析：这类题目可利用“可导奇函数的导函数为偶函数，可导偶函数的导函数为奇函数”来解决.

2.解题策略：先对函数求导，再结合三角函数奇偶性求解.

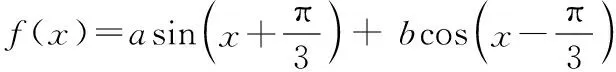
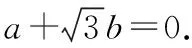
类似题型还有：

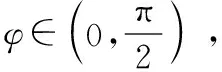
本题也是先由()是偶函数可得导函数为奇函数,必过原点求出,再结合三角函数图像之间关系得以解决问题.

3.教学小结：此类题型引导我们在教学中注重导函数与原函数之间的奇偶性特征的内在联系.

(三)对称性问题

1.试题分析：对称性是三角函数的重要特征之一，特别在三角函数中，当函数取到最值时，若直线=为对称轴，则′()=0.

2.解题策略：利用在三角函数最值点处导数值为0，即切线斜率为0的几何意义来解决问题.由于三角函数图像的特殊性质，结合导数可知最值点处导数值为零，对于这一特殊性质，教师在教学中应注重强调分析，使学生加深印象，并能学以致用.

5已知当=时，()= sin-2cos，∈取最大值，求cos的值.

类似题型还有：

6已知函数()=sin(π+)-2cos(π+)(0<<π)的图像关于直线=1对称，求sin 2的值.

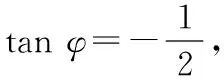
3.教学小结：选填试题常常是求值运算，学生对于三角诱导公式、倍角公式、图像必须能够熟练运用.

四、由导数求三角函数最值问题策略研究

1.试题分析：试题虽然是最值问题，但实际也是借助导数考查三角函数的单调性，从而求出三角函数最值.

2.解题策略：最值问题往往需要结合导数分析函数单调性，从而得到最值位置.

7(2018年全国Ⅰ卷16题)已知()=2sin+sin 2，求()的最小值.

3.教学小结：教师在教学中一定要引导学生利用导数工具研究三角函数单调性，最值在连续函数的极值或端点值中产生.全国卷中还有许多这样的题目，例如：()=cossin 2，研究()的图像的对称中心、对称轴，()的最大值、奇偶性，借助求导加换元法，研究导函数图像，从而得到原函数的全方位的特征.

五、由导数求三角函数极值点问题策略研究

1.试题分析：借助求导，结合三角函数的图像和性质，再紧扣极值、极值点概念进行求解.这类题目要求学生对极值与极值点概念有深刻认识并掌握.

2.解题策略：极值点位置分析离不开导数的单调性与图像的综合分析.

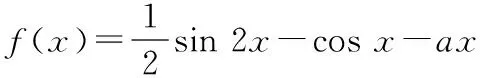
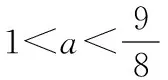
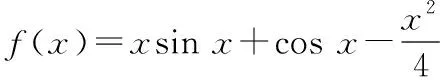
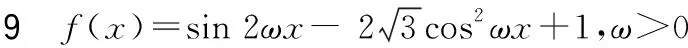
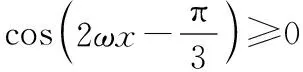
3.教学小结：极值点概念、掌握导数应用与三角函数图像的结合是解决此类问题的关键.

六、借助导数求三角函数零点问题策略研究

1.试题分析：利用导数解决三角函数的零点问题，通常要与零点存在性定理结合，往往证明某个区间上存在唯一零点.

2.解题策略：零点问题综合性强，归根结底离不开单调性分析.

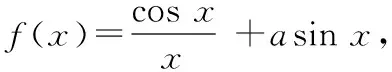
借助导数求三角函数零点问题，还有：

11已知()=sin 2的图像与直线2--π=0(>0)恰好有三个公共点，这三个点的横坐标从小到大分别为,,，求(-)tan(-2)的值.

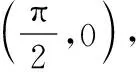
3.教学小结：三角函数零点问题，往往需要数形结合，再利用导数工具，要求教师培养学生综合分析能力.

七、结束语

综上所述，受到新高考改革的影响，为了帮助学生做到举一反三、学以致用，真正意义上提高综合解决问题的能力，教师要注重为学生讲解解题方法策略与技巧.尤其对于三角函数和导数相结合的“联姻”试题来说，教师要教会学生运用多种方法解题，发散学生思维，使学生克服数学学习上的障碍，树立信心，提高效果，以达到数学教育教学的立德树人目标.