基于麻雀搜索算法和滞后效应的土石坝渗流监控模型
2022-09-12宋锦焘段梦强曾志全
宋锦焘,袁 帅,段梦强,杨 杰,曾志全,黄 勇
(1.西安理工大学水利水电学院,陕西 西安 710048; 2.西安理工大学省部共建西北旱区生态水利国家重点实验室,陕西 西安 710048;3.中国电建集团华东勘测设计研究院有限公司,浙江 杭州 311122)
土石坝因造价低、环境适应性好、施工难度低等特点,在世界大坝工程建设中应用最为广泛,占大坝总量的80%以上[1],因此,土石坝的安全问题受到高度关注。随着土石坝竣工蓄水,受库水位、温度等外部荷载的联合作用,可能出现不均匀沉降、滑坡、裂缝等危及坝体安全的问题,其中渗流破坏导致的事故或垮坝占土石坝事故总数的30%~40%[2]。渗流监测是土石坝渗流安全分析的重要内容之一,土石坝渗流监测主要内容包括坝体、坝基、绕坝渗流以及渗漏量,通过分析土石坝渗流监测资料,建立土石坝渗流监控模型,对土石坝渗流性态和发展趋势进行安全监控和预测预报,从而定量评价土石坝的渗流安全性态[3-4]。
土石坝渗流主要受库水位、降水量及时效等因素影响,其中库水位、降水量对土石坝的渗流具有明显的滞后效应,即测压管水位出现峰谷值的时刻始终比库水位及降水量的峰谷值时刻滞后。这主要与库水位的高低、降水量的大小以及筑坝材料的渗透性、渗流路径的长短有关,导致测压管水位不能及时随库水位及降水量的变化而变化[5-6]。为了更好地分析和评价土石坝的渗流变化规律,在土石坝渗流压力监控模型中合理考虑库水位、降水量等环境量的滞后效应,得到较优的土石坝渗流监控模型具有较大的实用价值[7]。
土石坝渗流的影响因素较多,滞后机理复杂,常用方法是采用前期库水位和降水量均值来表示渗流滞后效应[8-10]。该方法虽在一定程度上提高了模型的精度,但其前期库水位和降水量均值的选取依靠经验,未考虑渗流滞后效应的动态变化,难以准确描述渗流滞后效应。张乾飞等[6-7,11-12]通过引入滞后效应函数来描述渗流的滞后效应,但大多采用同一滞后效应函数考虑库水位和降水量的滞后效应,极少考虑其差异性;李俊等[13]对比分析了几种估计环境量滞后时间的方法;庞琼等[14]考虑了库水位和降水量滞后效应的差异性,分别引入正态分布函数和对数正态分布函数描述库水位和降水量的滞后效应,构建了更加合理的模型,得到了较好的预测结果,但滞后效应函数的选取仍可优化。本文考虑库水位和降水量对土石坝渗流滞后影响的差异性,分别引入正态分布函数和瑞利分布函数来构建渗流压力滞后效应函数,构建考虑滞后效应的土石坝渗流压力监控模型,采用麻雀搜索算法[15](sparrow search algorithm,SSA)和偏最小二乘回归[16-17](partial least squares regression,PLSR)优化求解滞后效应参数和模型回归系数,并通过工程实例验证了模型的合理性和有效性。
1 模型构建
1.1 未考虑滞后效应的土石坝渗流监控模型
常规渗流监控模型未考虑库水位和降水量的滞后效应,仅将其作为影响因子进行建模。常规的土石坝渗流监控模型(模型Ⅰ)为
h=a0+a1H+a2P+a3θ+a4lnθ
(1)
式中:h为测压管水位;a0为常数项;a1、a2、a3、a4为回归系数;H、P为库水位、降水量当日实测值;θ为时效分量,自首次观测日起,每增加1天,θ的值增加0.01。
1.2 考虑上游库水位与降水量前期均值的渗流监控模型
改进的渗流监控模型在常规渗流监控模型的基础上,选取库水位、降水量前期均值作为影响因子,得到的渗流监控模型(模型Ⅱ)为
1.3 基于滞后效应函数的渗流监控模型
基于上述渗流监控模型,本文重点考虑库水位、降水量与测压管水位之间的滞后效应及其差异性,引入不同的滞后效应函数,构建渗流监控模型中的水压分量与降水分量的表达式,建立基于滞后效应函数的土石坝渗流监控模型。
1.3.1考虑滞后效应的水压分量
测压管水位滞后库水位变化的原因大致可以分为以下3个方面:①水压力的传播需要时间,即库水位的变化引起渗流场内某点水压力变化需要一定时间,有一定的滞后效应;②测压管充放水需要时间,即测压管水位与测点实际水位达到平衡需要时间;③非饱和土的充水和饱和土体中的水消散需要时间[18]。因此,在大坝渗流实际监测中,测压管水位始终滞后于库水位变化,并且测压管水位是该时刻及该时刻以前库水位连续变化影响的瞬态结果。假设t时刻测压管水位受t时刻及该时刻以前n个库水位影响,水压分量Hd可表示为
Hd=f(t,Ht,Ht-τ1,Ht-τ2,…,Ht-τn-1,w1,w2,…,wn)
(3)
式中:wi为第i(i=1,2,…,n)个库水位Hi对水压分量的影响权重;τk(k=1,2,…,n-1)为滞后时间,τk≥0;Ht、Ht-τk为对应时刻的库水位。

(4)
假设库水位的影响权重分布函数为w(t),由库水位和测压管水位是随时间连续变化的函数可知该分布函数也是时间的连续函数。同时,库水位对测压管水位的作用是一个逐渐上升、达到峰值后逐渐下降的过程,根据统计分析,其影响基本服从正态分布[18-19],故引入正态分布函数作为库水位滞后效应函数,即w(t)呈现正态分布:
(5)

式中:α1为调整系数;τH为库水位滞后时间;β1为库水位效应分布参数。
综上,在t=t0时刻的水压分量为

(6)
1.3.2考虑滞后效应的降水分量
降水量对测压管水位作用也有明显的滞后效应,但降水量对测压管水位的滞后效应与库水位不同。降水落到地表后大致分为两部分:汇流成地表径流和入渗成地下径流,其中入渗部分的降水量对测压管水位变化起决定作用[20]。降水不是一个连续的过程,存在一定的周期,对测压管水位的影响是一个较快的上升和较慢的下降过程[7]。当降水量的滞后时间较短时,降水量的影响权重较大,且集中在滞后时段附近;当降水量的滞后时间较长时,其滞后影响的时域相对长些,降水量的影响权重也较小。瑞利分布是最常见的用于描述平坦衰落信号时变特性的一种分布类型,瑞利分布函数相较于对数正态分布函数[14]能够较好地描述降水量的滞后效应[21],故引入瑞利分布函数作为降水量滞后效应函数,即w(t)呈现瑞利分布:
(7)
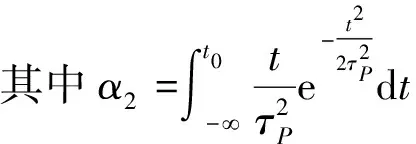
式中:α2为调整系数;τP为降水量滞后时间。
因此,在t=t0时刻的降水分量Pd可表示为
(8)
式中:Pt为t时刻降水量;γ为入渗变换指数,根据经验取0.4[6]。
综上,考虑滞后效应的渗流监控模型(模型Ⅲ)为
(9)
1.4 模型参数求解方法
1.4.1麻雀搜索算法
麻雀搜索算法是受麻雀觅食行为和反捕食行为启发而提出的一种新的群智能优化算法,该算法同其他群智能优化算法相比具有较高的搜索精度、稳定性好、收敛速度快、鲁棒性强等特点,其原理如下[22]:将麻雀种群分为发现者和加入者,通过种群比例因子控制发现者和加入者数量,并引入了侦察预警机制。其中发现者为所有加入者提供觅食的区域和方向,加入者利用发现者来获取食物,同时部分加入者会监控发现者以争夺食物资源。而当种群中有麻雀发现了捕食者或者意识到危险时,种群会立即做出反捕食行为。
假设在一个d维搜索空间中,存在n只麻雀,在每次迭代的过程中,发现者的位置更新如下:
(10)
式中:Xij为麻雀i在第j维中的位置信息;K1为一个随机数,K1∈(0,1];t为当前迭代次数;tmax为最大迭代次数;Q为服从正态分布的随机数;L为元素全部是1的1×d的矩阵;U、V分别为预警值和安全值,U∈[0,1],V∈[0.5,1]。
加入者的位置更新如下:
(11)
其中A+=AT(AAT)-1
式中:Xw为当前全局最差位置;Xg为当前发现者所占据的最优位置;A为元素随机赋值是1或-1的1×d的矩阵。
当意识到危险时,麻雀种群会做出反捕食行为,这些意识到危险的麻雀占总数量的10%~20%,其位置更新如下:
(12)
式中:Xb为当前全局最优位置;K2为服从0-1正态分布的随机数;K3为一个随机数,K3∈[-1,1];fi、fw、fg分别为当前麻雀的个体、全局最差和全局最优适应度值;ε为常数,以避免分母出现0的情况。
其算法流程为:①随机初始化麻雀种群并定义相关参数,设置最大迭代次数;②计算初始种群的适应度并将其排序进而选择出当前最优位置和最差位置;③更新发现者的位置、加入者的位置以及意识到危险的麻雀的位置;④获得当前最优位置,如果当前最优位置优于上一次迭代的最优位置则更新操作,否则不进行更新操作,并继续进行迭代操作直到满足条件为止;⑤得到最终全局最优位置和最优适应度值。
1.4.2渗流监控模型参数求解
在模型求解过程中,为避免渗流监控模型中各影响因子之间的多重共线性干扰,采用偏最小二乘回归方法求解模型回归系数,能够有效克服影响因子之间的多重共线性影响[17]。而模型中的滞后效应参数,以模型的复相关系数为目标函数,运用麻雀搜索算法优化,得到最优滞后效应参数,具体流程如图1所示。
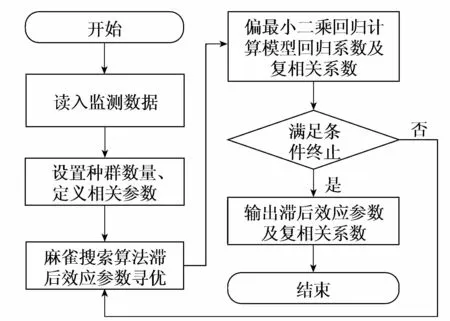
图1 模型求解流程
2 实例验证
2.1 工程概况
某大(2)型水利枢纽由土石坝、溢洪道、泄洪洞、排沙洞、引水洞、灌溉管等组成,以发电为主,兼有防洪、灌溉、渔业等功能。大坝为碾压式壤土心墙土石坝,最大坝高101.8 m,水库总库容5.21亿m3,坝顶长297.36 m。该工程的监测项目包括大坝的外部变形监测、渗流监测、内部监测等,大坝渗流监测布置见图2,各测压管横剖面布置见图3。
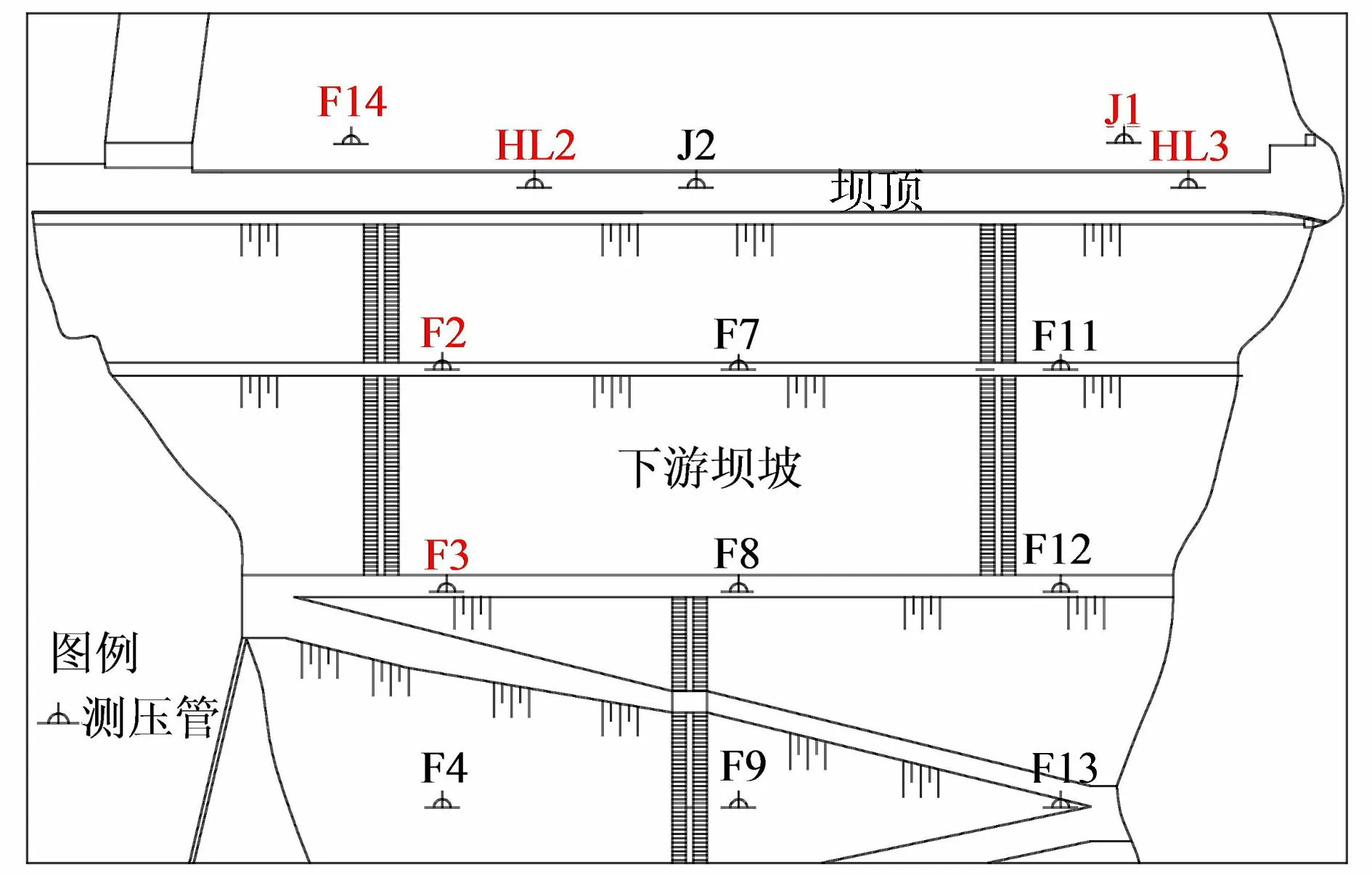
图2 大坝渗流监测布置

图3 大坝渗流监测横剖面
对于该土石坝,壤土心墙起主要防渗作用。为分析心墙的防渗作用,根据实际监测资料(1977—2020年),选择监测资料较完整的上游坝坡测压管F14、J1和心墙测压管HL2、HL3以及下游坝坡测压管F2、F3的2010年监测资料进行对比分析,其库水位、各测压管水位过程线以及降水量见图4。由图4可知,上游坝坡测压管水位与上游库水位变化趋势几乎同步;心墙测压管水位整体比上游库水位低10~15 m,其变化趋势不如库水位变化明显,周期性变化比库水位变化滞后,受降水量影响较小,存在心墙测压管水位低于上游水位的现象。这主要是心墙测压管水位不能及时响应上游水位的变化以及测压管充放水需要时间引起的,说明上游水位对心墙测压管水位影响具有明显的滞后效应;下游坝坡测压管水位明显低于库水位和心墙测压管水位,无明显随库水位变动的趋势,水位变化受降水量影响较大。
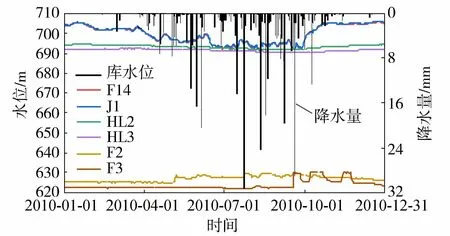
图4 库水位、降水量和测压管水位过程线
2.2 滞后效应参数计算及结果分析
根据测压管监测数据,通常库水位、降水量每天都有测值,为了便于计算,把连续型积分改为离散型积分,根据3σ原则,积分区间取效应分布参数的3倍。采用MATLAB编程,设置种群数量为30,最大迭代次数为50,运用麻雀搜索算法求解滞后效应参数,结果如表1所示。
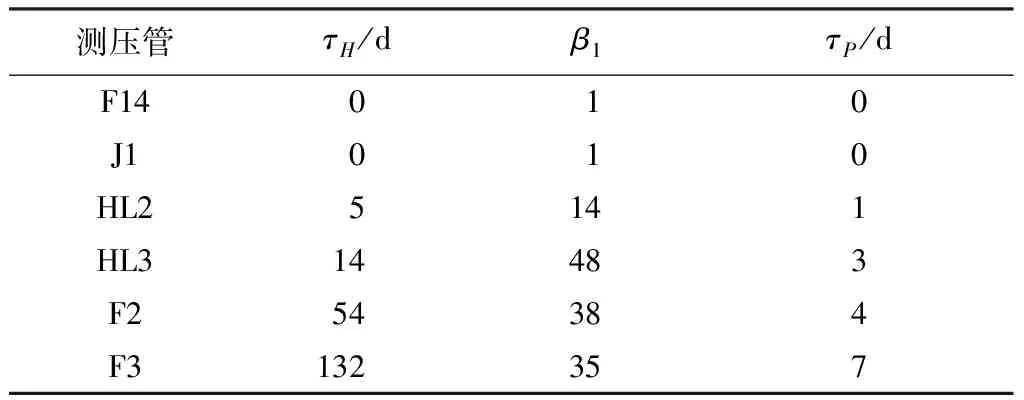
表1 滞后效应参数计算成果
由表1可知,上游坝坡测压管F14、J1水位同步上游库水位变化,降水量对上游坝坡测压管水位的滞后影响也不显著,这与上游坝坡的主要筑坝材料是透水性较好的砂砾石与堆石有关;心墙测压管HL2、HL3的水位变化分别滞后库水位5 d和14 d,降水量分别滞后1 d和3 d,说明大坝心墙起着良好的防渗作用,同时两心墙测压管水位的滞后效应有差异,这与心墙的碾压质量、测压管的布置以及大坝的运行管理有关;下游坝坡测压管F2、F3的水位变化分别滞后库水位54 d和132 d,降水量分别滞后4 d和7 d,说明测压管离上游越远滞后时间越长,符合渗流的一般变化规律。
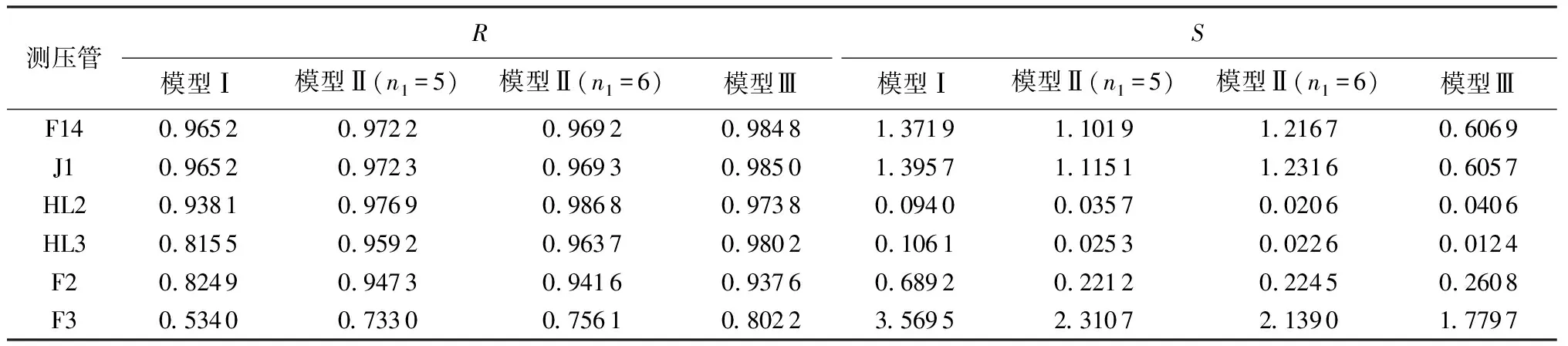
表2 各渗流监控模型的复相关系数和剩余均方差
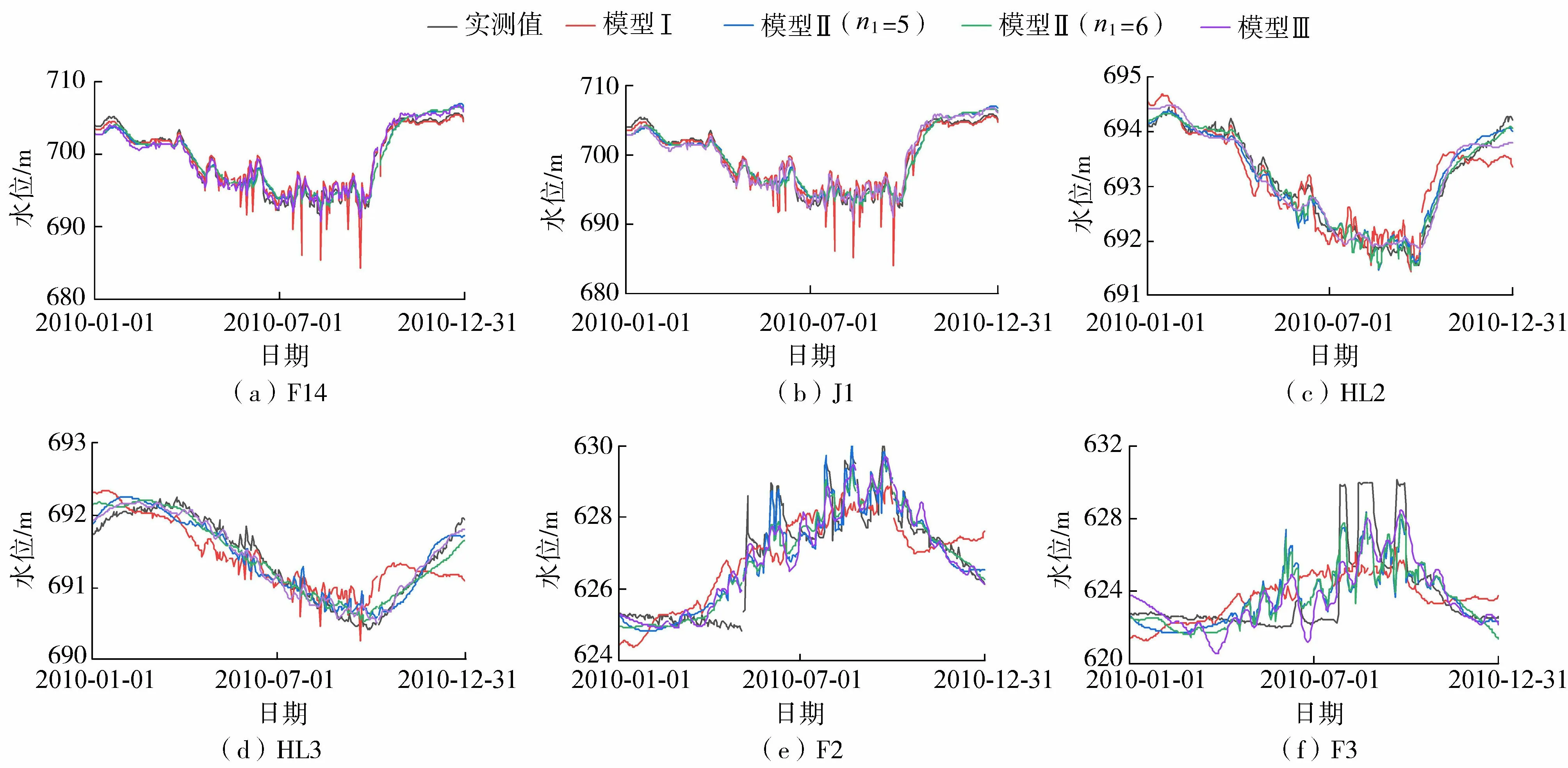
图5 各测压管水位实测过程线与拟合过程线
2.3 模型计算及结果分析
由偏最小二乘回归分析得到各测点、各模型的复相关系数R、剩余均方差S见表2。各测压管水位实测过程线与拟合过程线见图5。
由表2和图5可知,考虑滞后效应的模型Ⅱ、模型Ⅲ比未考虑滞后效应的模型Ⅰ的复相关系数要高,剩余均方差较小,拟合精度较高,进一步说明在土石坝渗流监控模型中考虑环境量的滞后效应是必要的。模型Ⅱ虽能提高拟合精度,但其拟合精度与选择的前期库水位时间长度有关,n1=6时与n1=5时的拟合精度相比较,上游坝坡测压管的拟合精度有所降低,而心墙测压管和下游坝坡测压管的拟合精度则有所提高,说明模型Ⅱ能提高模拟精度,但拟合精度会随着所选取的平均时段长度变化而变化,具有较强的主观性,且无法定量评价渗流的滞后效应。相比较而言,模型Ⅲ不仅具有较高的拟合精度,且计算结果受主观因素影响较小,通过多个测点监测数据拟合结果可以看出,大部分拟合结果模型Ⅲ精度远高于模型Ⅱ,小部分拟合结果模型Ⅲ精度与模型Ⅱ接近,说明模型Ⅲ更为合理有效,避免了受参数随机选取的影响,且能对库水位和降水量的滞后时间进行一个初步估计。
为进一步验证本文滞后效应分布函数假定的合理性和有效性,将文献[14]中以对数正态分布为降水滞后效应函数的渗流监控模型应用到本文实例中,得到各滞后效应参数、复相关系数和剩余均方差见表3。
与模型Ⅲ的计算结果对比可知,对于上游坝坡测压管F14、J1,两模型的计算结果一致,但模型Ⅲ精度更高;对于心墙的测压管HL2、HL3,两模型的计算结果相近,模型的精度相差不大;对于下游坝坡测压管F2、F3,模型Ⅲ精度也略高。说明模型Ⅲ是合理有效的,且以瑞利分布来描述各降水量的影响权重更加合理。
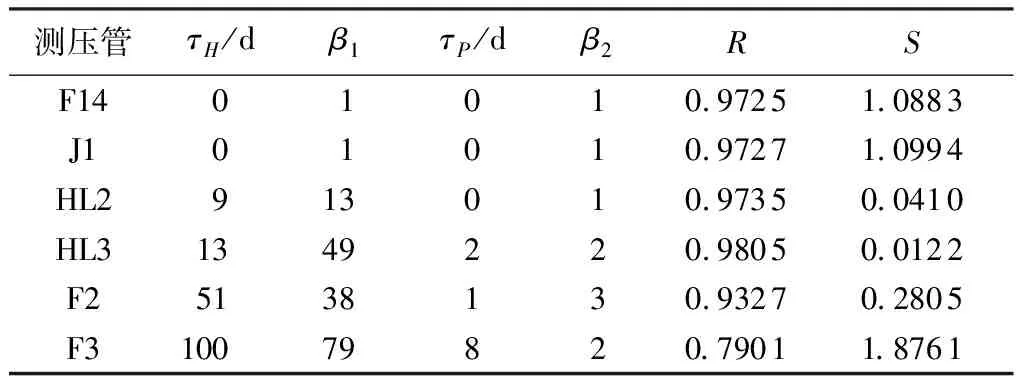
表3 文献[14]模型计算结果
3 结 语
对土石坝而言,库水位、降水量对渗流压力影响具有显著的滞后效应,渗流监控模型中影响因子的不同滞后效应表达式对模型的精度影响较大,本文通过引入不同的分布函数,构建了考虑滞后效应的水压分量和降水分量表达式,通过某土石坝实际工程对比验证了该模型具有较高的精度。但土石坝渗流的滞后机理复杂,如何针对不同工程的实际情况,并基于土石坝渗流压力监测数据的时空分布特征,引入先进的人工智能算法,完善土石坝渗流滞后效应分析理论,仍需进一步深入研究。
