白鹤滩水电站输水发电系统水力干扰稳定性分析

2022-09-12陈益民程文超周建旭孙洪亮

水利水电科技进展 2022年5期

陈益民，程文超，周建旭，杨飞，孙洪亮

(1.中国电建集团华东勘测设计研究院有限公司，浙江杭州 311122； 2.河海大学水利水电学院，江苏南京 210098)

水电站输水发电系统的稳定运行是保障电网安全可靠的重要前提。在水电站运行实践中，水力系统、机械系统以及电气系统的特性相互耦合，直接影响水电站的安全稳定运行[1]。因此，应针对水电站输水发电系统开展全面的稳定性分析，对于两机或多机共水力单元的情况，甩荷或增荷机组对运行机组的影响较为突出，应着重进行水力干扰稳定性分析。

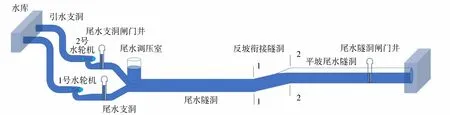
图1 水电站输水发电系统布置示意图

在对水电站水力-机械系统进行稳定性分析时，常采用刚性模型或低阶弹性模型[2-3]来描述水体的动态特性，并将描述系统动态特性的微分方程线性化，得到状态方程组，通过数值求解以评估系统的稳定性和机组的调节品质[4-6]，或者推导出相应的特征方程或传递函数，进行调节控制研究[7-9]。针对水电站稳定性，诸多学者开展了较为广泛而深入的研究。杨建东等[10]研究了上下游双调压室系统稳定域的变化规律，推导出稳定域干涉点和共振点的解析公式。郭文成等[11]建立了水轮机调节系统非线性数学模型，将Hopf分岔理论应用到变顶高尾水洞水电站水轮机调节系统的稳定性研究。Yu等[12]研究了水轮机-调速器系统状态方程的表述特征，利用矩阵变换方法，建立了一种求解状态方程系数矩阵的新方法。Zhou等[13]针对单管单机水电站，考虑调速器不同调节方式，建立了相应的状态方程，分析了小负荷扰动下的动态过程。翟晓娟等[14]考虑水力、机械、电气系统的耦合作用，建立了水电机组稳定性非线性数学模型，分析了孤网运行时水电机组的水力干扰稳定性。Chen等[15]提出了一种多目标综合指标，并使用该指标对调速器的参数进行优化，为在尾水波动条件下的稳定性分析提供了理论支持。Yu等[16]利用Jordan标准形式的状态矩阵解耦，推导了无量纲转轮转速的显式公式，采用直接求解方法，优化选择PID控制器参数。马安婷等[17]基于水力系统振动特性分析方法，建立输水发电系统总体矩阵，能够准确求解复杂输水发电系统的运行稳定域。周建旭等[18]结合设置上下游双调压室的长引水式水电站输水系统的水力特性，探讨了上下游调压室系统水力干扰稳定性等特殊水力学问题。Huang等[19]对孤立电网下复杂水电站小波动过渡过程中的调速器参数敏感性进行了研究。李玲等[20]构建了超长引水隧洞水电站单机无穷大电网的仿真模型，研究了系统的小波动稳定性。上述研究主要侧重于小波动稳定性分析，而水力干扰稳定性研究相对较少。

白鹤滩水电站单机容量达百万千瓦，机组运行水头为163.9～243.1 m，具有单机容量巨大、运行水头变幅大的特点。该水电站输水发电系统采用单管单机引水、两机共用尾水调压室和尾水隧洞的布置方式，其中尾水系统采用“三段变坡”的形式，包括有压尾水隧洞、坡度较大的反坡衔接隧洞和平坡尾水隧洞，而平坡尾水隧洞中会发生明流、满流，以及明满流现象。因此，本文基于有压输水系统特征线法，引入明满流尾水隧洞瞬变流分析的特征隐式格式，以便准确描述尾水系统中可能的复杂流态，同时考虑调速器频率调节模式，建立输水发电系统稳定性分析和调控模型，并结合白鹤滩水电站典型水力单元开展水力干扰稳定性分析，阐明受扰机组的稳定运行及其影响因素，揭示尾水系统复杂流态对系统稳定运行的影响，为制定可靠有效的调节控制策略提供技术支撑。

1 输水发电系统稳定性分析模型

1.1 输水系统瞬变流分析的数学模型

白鹤滩水电站输水发电系统布置见图1，其尾水系统的反坡衔接隧洞和平坡尾水隧洞在过渡过程中可能出现无压流、有压流，以及明满流现象。图1中1—1断面为反坡衔接隧洞进口断面，2—2断面为反坡衔接隧洞出口断面，亦为明满流隧洞段串联节点。

输水发电系统的有压输水部分，即从水库进水口至反坡衔接隧洞进口(断面1—1)，采用有压输水系统特征线法来描述其瞬态特性，可求解出计算断面的测压管水头和流量，相应的特征方程为

C+：HP=Cp-SpQP

(1)

C-：HP=Cm+SmQP

(2)

式中：H为断面瞬时测压管水头；Q为断面瞬时流量；Cp、Sp、Cm、Sm均为有压输水系统特征方程的已知系数；下标P对应的参数为计算节点未知量。

输水发电系统的明满流隧洞部分(运行尾水位低于尾水隧洞出口洞顶或在尾水隧洞出口洞顶附近)，即从始终为有压流的反坡衔接隧洞进口断面1—1至平坡尾水隧洞出口，采用明渠水流特征隐式格式来描述其动态特性，可求解出计算断面的瞬时水深和流量，相应的特征方程为

a1jΔhj-1+b1jΔQj-1+c1jΔhj+d1jΔQj=e1j

(3)

a2jΔhj+b2jΔQj+c2jΔhj+1+d2jΔQj+1=e2j

(4)

式中：Δh、ΔQ分别为断面水深和流量的增量形式；aij、bij、cij、dij均为系数(i=1,2)；下标j为计算断面编号。

基于特征方程(3)和(4)，结合尾水闸门井节点的流量连续条件、水头平衡条件和闸门井水位波动方程，可建立尾水闸门井边界的数学模型；同时，考虑反坡衔接隧洞进口断面、明满流隧洞串联节点、明满流隧洞出口的流量连续条件和水头平衡条件，建立相应边界的数学模型。

有压输水和明满流模拟段的交界面(即始终为有压流的反坡衔接隧洞进口断面1—1)，满足流量连续条件和水头平衡条件(即有压模拟段出口断面流量等于明满流模拟段进口流量，以及有压模拟段出口测压管水头等于明满流模拟段进口水深加上洞底高程)，据此可建立融合有压输水系统特征线法和明满流隧洞特征隐式格式的输水系统瞬变流分析模型。在瞬变流计算分析过程中，若明满流模拟段某计算断面的瞬时水深近似等于断面洞高，则该计算断面为明满流分界面。

1.2 水轮发电机组的动态分析模型

白鹤滩水电站输水发电系统的稳定性分析模型应能够准确描述百万千瓦机组的综合特性及其对系统运行稳定性的影响。白鹤滩水电站左岸输水发电系统的水轮机型号为D545A-F15，结合机组模型特性曲线，可得到反映水轮机全特性的离散数据，包括流量特性Q11=f1(n11,a)和效率特性η=f2(n11,a)，其中Q11、n11、η和a分别为机组单位流量、单位转速、效率和导叶开度，f1和f2表示不同的函数关系，见图2。

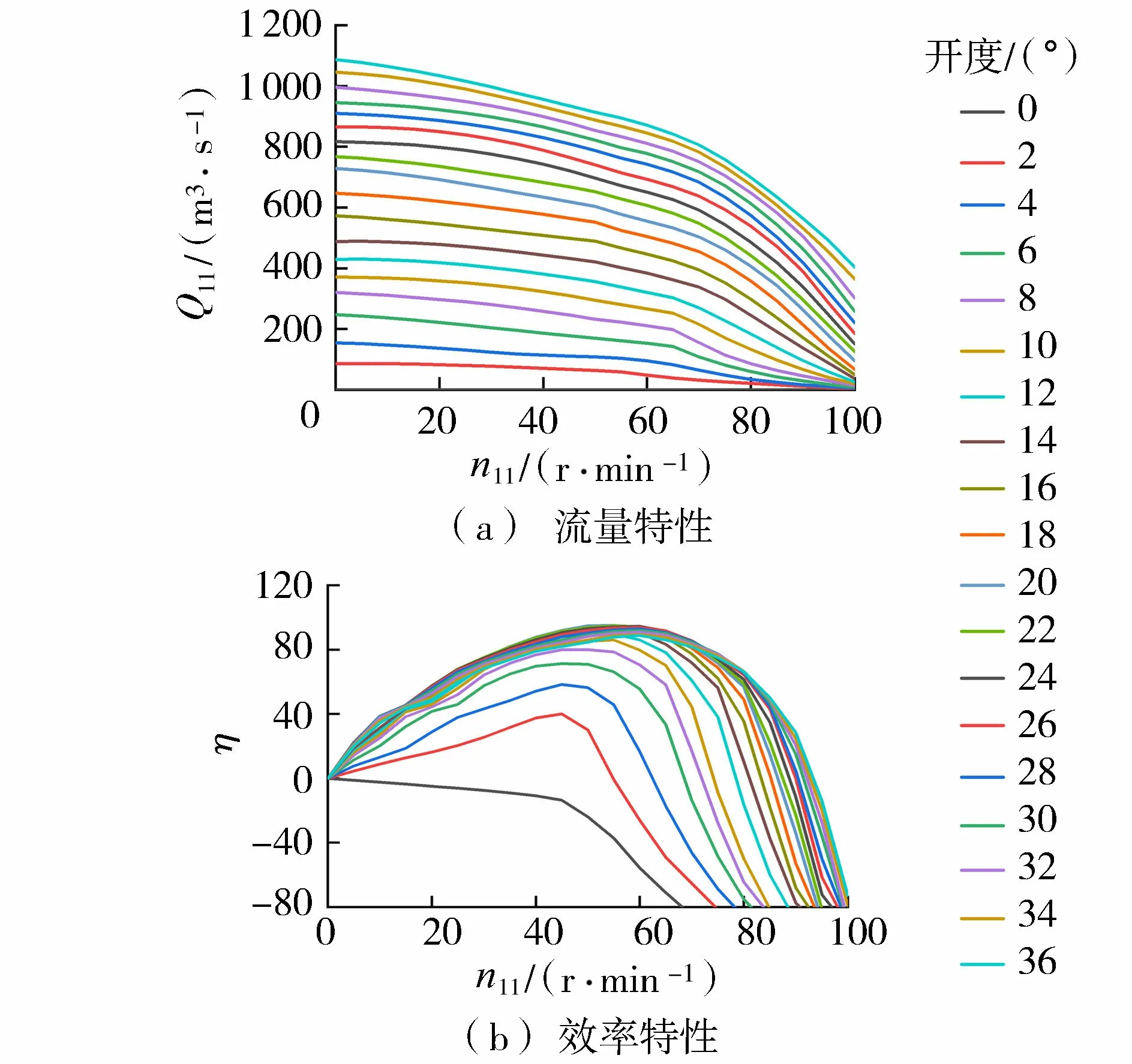
图2 水轮机D545A-F15综合特性曲线

白鹤滩水电站右岸输水发电系统的水轮机型号为A1181a，其全特性曲线见图3，包括流量全特性曲线Q11=f1(n11,a)和力矩全特性曲线T11=f3(n11,a)，其中T11为机组单位力矩。

描述机组节点的方程有：

H=(Cp1-Cm2)-(Sp1+Sm2)Q

(5)

P=γQHη

(6)

(7)

(8)

(9)

式中：H、Q、P、n分别为机组运行水头、流量、出力、转速；γ为水的容重；D1为转轮直径；Cp1、Sp1、Cm2和Sm2均为基于有压输水系统特征方程的已知系数。

结合式(5)～式(9)，以及水轮机模型综合特性曲线Q11=f1(n11,a)和η=f2(n11,a)(左岸机组)，或者Q11=f1(n11,a)和T11=f3(n11,a)(右岸机组)，则可求解得到任一瞬时水轮机节点的相关参数，包括蜗壳进口测压管水头和流量、尾水管进口测压管水头和流量、机组瞬时出力或力矩等。

描述扰动机组动态特性的状态方程为

(10)

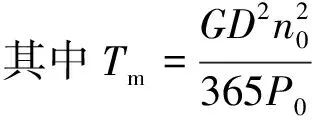
式中：φ、p分别为机组相对转速变化量和相对出力变化量；t为时间；x为外扰动；Sg为负荷自调节系数；Tm为机组启动时间常数;P0、n0、GD2分别为机组初始出力、初始转速和转动惯量。基于式(10)和机组的综合特性，可得到受扰机组的瞬时转速。

1.3 调速器的状态方程

考虑到白鹤滩水电站在电网中的重要性和机组的运行稳定性要求，基于调速器的频率调节模式，进行系统的调节控制分析。在频率调节模式下，调速器采用PID调节规律，将导叶开度作为反馈值，实时跟踪机组实际功率。将调速器频率调节模式的状态方程[13]耦合机组的状态方程(10)以及输入扰动，即可确定机组和调速器的状态变量值，包括机组导叶相对开度等。

1.4 融合输水系统复杂瞬变流分析的输水发电系统调控模型

融合输水系统明满流等复杂瞬变流分析的数学模型、考虑机组综合特性的水轮发电机组动态分析模型和调速器频率调节模式的状态方程，构建形成白鹤滩水电站百万千瓦机组及输水发电系统的调节控制模型。

表2 左岸1号水力单元水力干扰过渡过程调节品质

基于所建立的白鹤滩水电站输水发电系统调节控制模型，进行水力-机械系统水力干扰稳定性分析，能够准确反映扰动机组和输水系统瞬态参数的较大幅度变化，以及受扰机组参数的动态变化过程和调节品质，并直观揭示输水发电系统在水力耦合下的水力干扰特性，特别是受扰机组的动态特性。

2 输水发电系统水力干扰稳定性

2.1 白鹤滩水电站参数

白鹤滩水电站地下厂房采用首部开发方式，左、右岸输水发电系统的布置格局相同，各布置8台混流式水轮发电机组，分为4个水力单元，引水系统采用单洞单机布置方式，尾水系统采用两机合一洞的布置方式，典型水力单元布置如图1所示。电站左岸水轮机型号为D545A-F15，单机额定出力为1 015 MW，额定流量为545.49 m3/s，额定水头为202 m，额定转速为111.1 r/min，转动惯量为36万 t·m2；左岸1号水力单元引水道长度l1为480.50 m，尾水支洞长度l2为259.75 m，尾水隧洞总长度l3为1 695.80 m。右岸水轮机型号为A1181a，单机额定出力为1 015 MW，额定流量为538.80 为m3/s，额定水头为202 m，额定转速为107.1 r/min，转动惯量为37万t·m2；右岸8号水力单元引水道长度l1为486.12 m，尾水支洞长度l2为240.15 m，尾水隧洞总长度l3为1 769.87 m。左岸1号和右岸8号水力单元尾水隧洞出口顶高程均为592.0 m，尾水调压室有效面积均为1 590.43 m2。

2.2 水力干扰分析工况

结合白鹤滩水电站典型水力单元，开展水力干扰过渡过程计算分析，评估发生水力干扰时运行机组的运行稳定性以及调节品质。已知调速器调节参数的整定值为：永态转差系数bp=0.04，相应比例常数KB=2.5、积分常数KI=0.385 1/s、微分常数KD=2.5 s。

表1给出了白鹤滩水电站左岸和右岸控制输水发电系统水力干扰稳定性分析的典型工况，其中工况D1和D2水库水位一列分别对应左岸1号和右岸8号水力单元的数值。

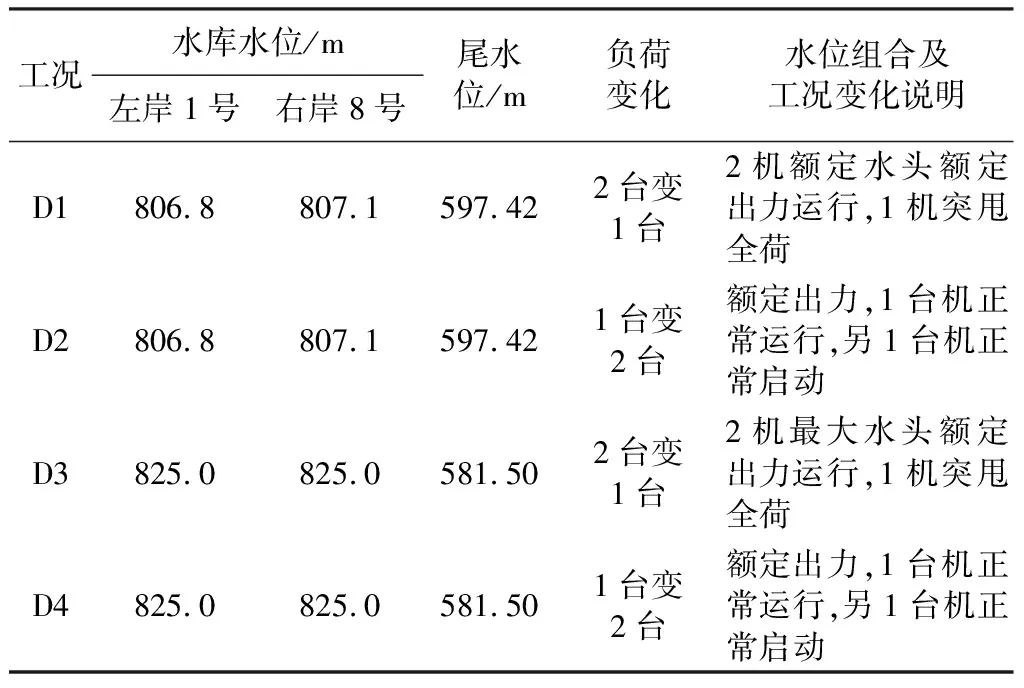
表1 水力干扰工况

2.3 受扰机组稳定性和调节品质分析

结合白鹤滩水电站左岸1号和右岸8号水力单元，以及相应的机组特性和导叶启闭规律，结合表1给出的水力干扰稳定性分析工况，进行受扰机组的运行稳定性分析，调节品质分析见表2和表3，表中给出了对应转速偏差为±0.2%和±0.4%时的调节时间。典型工况频率调节模式下受扰机组的转速和机组出力的动态过程见图4和图5。

图4和图5表明：依据整定的调速器参数、电网负荷自调节系数等相关参数，左岸1号和右岸8号水力单元受扰机组转速是衰减的，水力干扰过渡过程是稳定的；受扰机组的出力发生明显的摆动，最大出力均未超出额定出力的105%，且超出力历时较短；受扰机组转速的衰减度均小于90%。随着机组运行水头的增大，受扰机组的调节品质明显改善，主要表现为调节时间缩短，振荡次数减小，最大偏差减小和衰减度增大，即甩荷工况D3相较于D1，增荷工况D4相较于D2，机组运行水头较大，受扰机组转速的波动明显减小，衰减明显加快。因工况D1运行水头明显较低，机组转速和出力动态过程振荡幅度较大，稳定性较差，同时工况D1对应运行开度为额定开度，受扰过程中受调速器接力器行程限制的影响，故工况D1和D3的水力干扰过渡过程存在较大差别。

表3 右岸8号水力单元水力干扰过渡过程调节品质分析

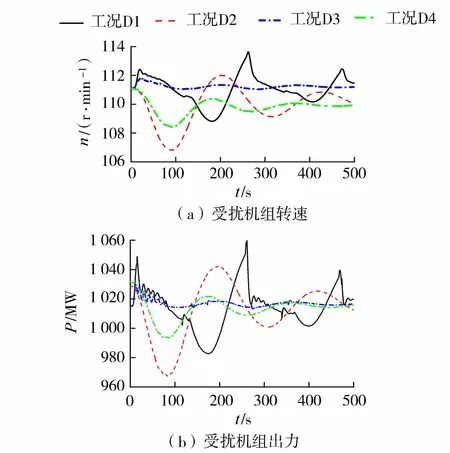
图4 左岸1号水力单元受扰机组转速、出力动态过程

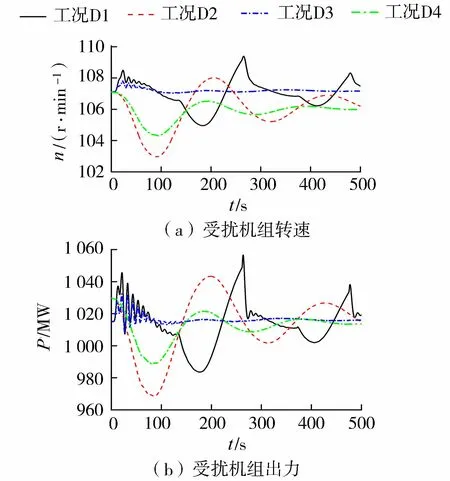
图5 右岸8号水力单元受扰机组转速、出力动态过程

2.4 尾水隧洞典型流态对系统稳定性的影响

左岸1号和右岸8号水力单元尾水隧洞洞顶高程为592.00 m，工况D1和D2尾水位为597.42 m，工况D3和D4尾水位为581.50 m，因此工况D1和D2尾水系统全线为有压流流态，而工况D3和D4在反坡衔接隧洞段出现明满交替流流态，高程较高的平坡尾水隧洞段出现明流流态。图6和图7分别给出左岸1号水力单元各工况尾水调压室水位和左/右岸典型水力单元明满流分界面动态过程线，以分析尾水隧洞典型流态对系统稳定性的影响。

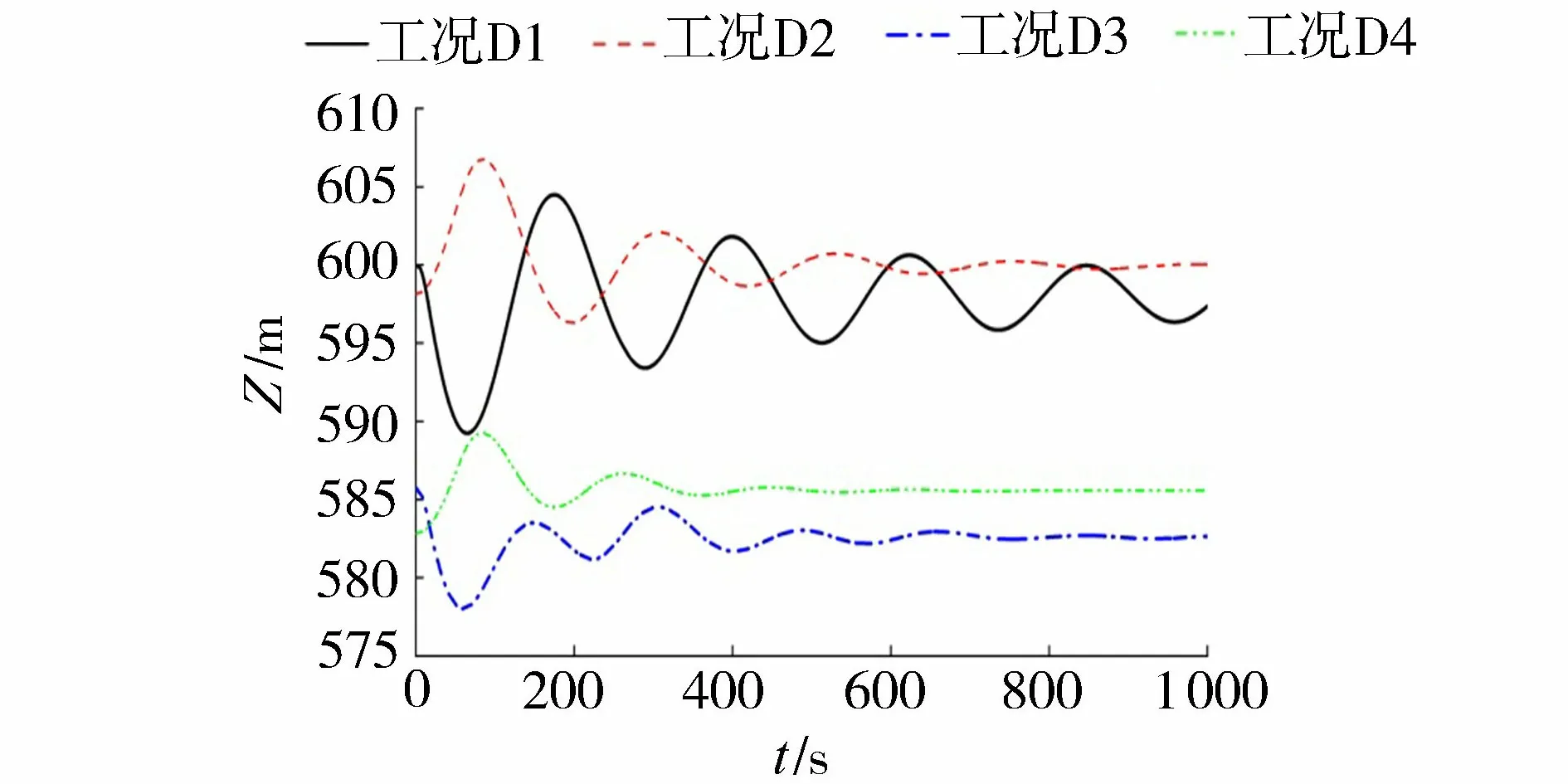
图6 尾水调压室水位动态过程线

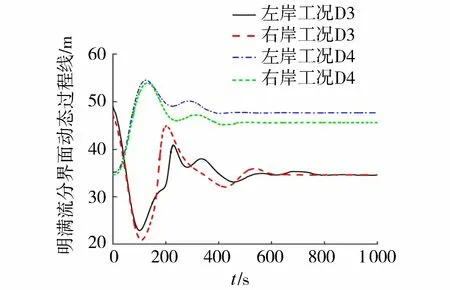
图7 明满流分界面动态过程线

图6表明：机组额定出力运行时，工况D1和D2运行水头相对较低，运行流量较大，调压室水位波动幅度较大，且增荷工况衰减较快；因工况D1和D2尾水隧洞全线有压，调压室水位波动周期较长，而工况D3和D4尾水隧洞下游段为明满流段或明流段，有压段长度缩短，调压室水位波动周期较短，同时运行水头相对较高，调压室水位稳定时间明显缩短，有利于系统的运行稳定性。图7表明：工况D3和D4尾水系统中出现明满流流态，对应的明满流分界面位于反坡衔接隧洞段，即在断面1—1和断面2—2之间移动，其下游侧始终为无压流，并且很快趋于稳定。

2.5 机组型号对系统稳定性的影响

白鹤滩水电站左岸1号水力单元的机组型号为D545A-F15，右岸8号水力单元的机组型号为A1181a。通过对比不同型号机组在相同工况下的机组转速和反坡衔接隧洞出口断面2—2测压管水头动态过程，分析不同机组型号时系统的水力干扰稳定性。图8和图9分别给出了甩荷工况D1和D3下机组转速变化相对量φ和反坡衔接隧洞出口(断面2—2)测压管水头H2变化过程线。

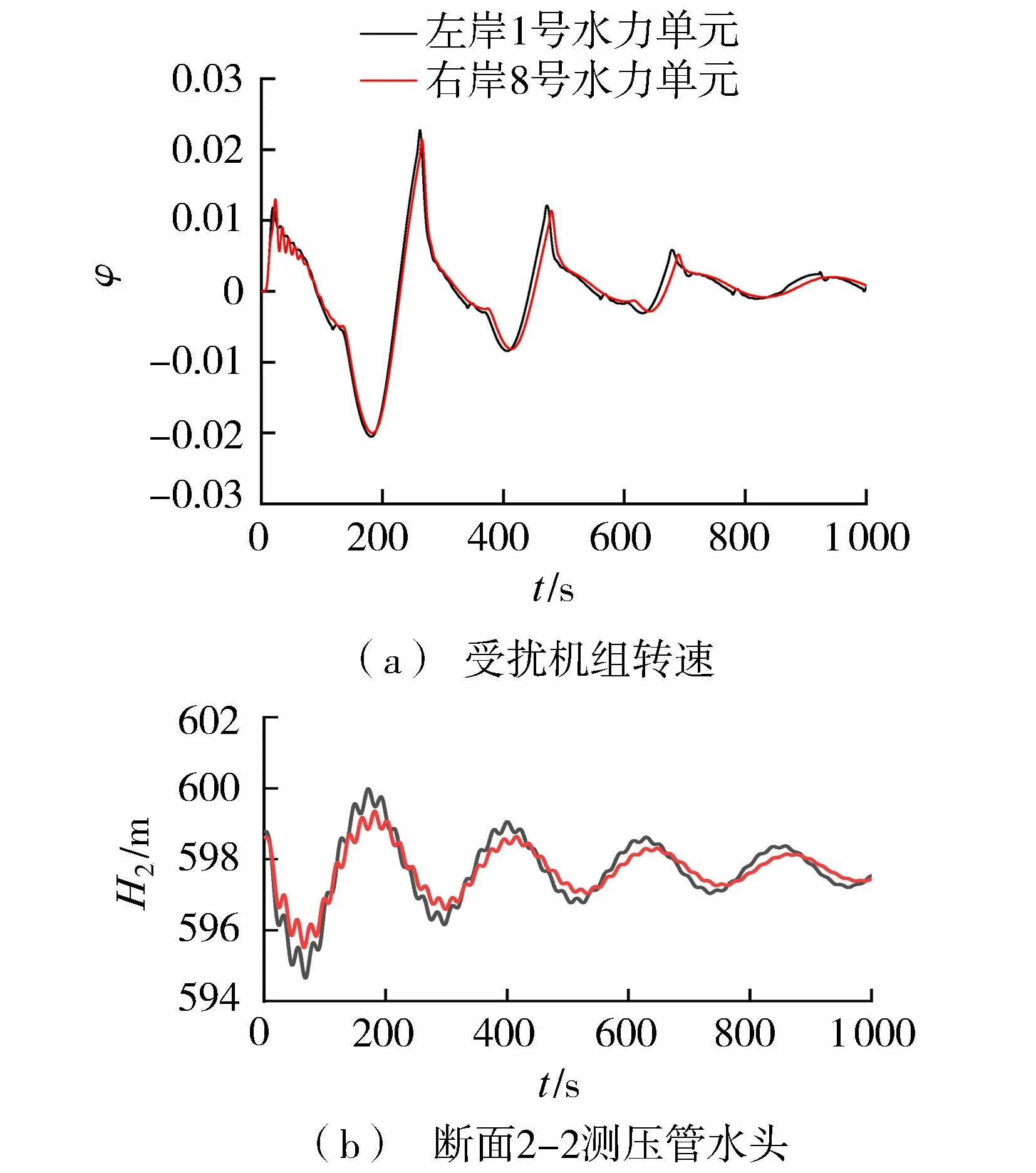
图8 工况D1下受扰机组转速及断面2—2测压管水头动态过程

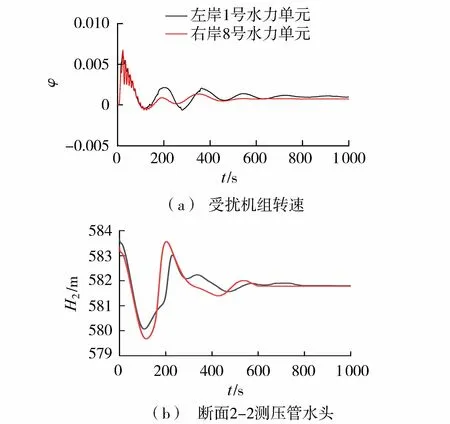
图9 工况D3下受扰机组转速及断面2—2测压管水头动态过程

图8和图9表明：在机组甩荷条件下，工况D1转速变化相对值的动态变化趋势基本一致，对应的机组调节品质评价指标接近(表2、表3)，而工况D3转速变化相对值衰减过程存在较明显的差别，即不同机组型号下，第1个调节周期内机组最大转速不同和振荡衰减趋势明显不一致，在调节过程中相关参数动态过程亦受不同的尾水隧洞明满流过渡段和明流段的影响；左岸1号和右岸8号水力单元输水系统特别是尾水系统布置存在一定的差异，其中8号水力单元尾水隧洞较长，表现出两个水力单元衔接隧洞出口断面2—2测压管水头的变化趋势基本一致，其中工况D1衔接隧洞出口断面为有压状态，呈周期性振荡衰减，右岸8号水力单元对应的振荡周期略长，工况D3衔接隧洞出口断面为无压状态，测压管水头快速衰减并趋于稳定。