砂土海床海底管道贯入的数值模拟

2022-09-12郑晓明张春会李雪婷田英辉李永靖

河北科技大学学报 2022年4期

郑晓明，张春会,,3，李雪婷，田英辉，李永靖

(1.辽宁工程技术大学土木工程学院，辽宁阜新 123000；2.河北科技大学建筑工程学院，河北石家庄 050018；3.河北省岩土与结构体系防灾减灾技术创新中心，河北石家庄 050018；4.墨尔本大学基础设施工程系，维多利亚墨尔本 3010)

深海油气输送管道一般直接铺设于海床上，在风浪流及自重等荷载作用下海底油气管道通常贯入海床10%～50%管道直径[1-3]。海底油气管道通常在高温高压环境下运行，产生的热胀应力超过海床土体所能提供的约束管道侧向屈曲和轴向整体位移的摩阻力时，管道就会发生屈曲或走管等失稳，造成管道破裂、油气泄漏，从而污染环境。海床土体对管道的约束力与管道贯入深度密切相关，因此准确预测海底管道贯入深度，对于分析其在位稳定性至关重要[4-7]。

国内外对海底管道贯入深度问题开展了很多研究，RANDOLPH等[8-10]基于上限解法和下限解法研究了黏土中管道贯入深度与土体抗力的关系。AUBENY等[11]采用有限元方法研究了海底管道在黏土海床中的贯入问题，提出了基于管-土界面摩擦系数的贯入深度与贯入阻力之间的经验公式。王腾等[12]、DUTTA等[13]、HAWLADER等[14]、CHATTERJEE等[15]、ULLAH等[16]分别采用耦合欧拉-拉格朗日(coupled Eulerian-Lagranginan，CEL)方法和RITSS(remeshing and interpolation technique with small strain)方法研究了土体的应变率效应和应变软化对于管道在黏土海床贯入阻力的影响。MERIFIELD等[17]采用任意拉格朗日-欧拉(arbitrary Lagranginan-Eulerian，ALE)方法研究了管道在黏土海床贯入过程中土体重度和隆起对于贯入阻力的影响。VERLEY等[18]通过开展模型试验研究了管道在黏土中贯入阻力和位移响应，提出了预测管道黏土中贯入深度的经验公式。DINGLE等[19]、CHEUK等[20]开展了管道在黏土中贯入的离心机试验，研究了管土相互作用，并通过粒子图像测速技术观测了管道贯入过程中土体的流动。这些研究主要聚焦于黏土海床海底管道贯入问题。在北海、墨西哥湾、印度尼西亚、中国南海和渤海等地深水区广泛分布着砂土海床，随着这些地区油气资源的开发，海底管道在砂土海床贯入问题的重要性日益凸显，然而目前对砂土海床海底管道贯入研究还较少。VERLEY等[21]通过试验对海底管道在砂土中贯入的位移-阻力进行了研究，提出了砂土海床管道贯入深度的经验预测公式。ZHAO等[22]为研究砂土中的管-土相互作用，开展了相关离心机试验和数值研究。中国现行的海底管道相关领域技术标准为《海底管道系统规范》[23]，但该规范中尚无相关砂土海床海底管道贯入深度的预测方法。目前国内外普遍采用的相关规范为挪威的船级社发布的DNV-RP-F114[24]，该规范建议采用地基承载力公式计算海底管道在砂土海床贯入过程中所受到的阻力。这些研究主要采用经验公式预测海底管道贯入，仅考虑内摩擦角对海底管道贯入深度的影响。内摩擦角确实是描述砂土海床强度的关键参数，然而海底管道贯入砂土是一个复杂的管土相互作用问题，除了砂土强度外，管-土界面特性和剪胀特性等也都可能影响海底管道的贯入深度。

本文基于CEL方法，建立海底管道贯入砂土海床的大变形有限元模型，通过数值仿真模拟海底管道在风浪流及自重等荷载作用下贯入砂土海床的过程，分析管-土界面特性、砂土强度和剪胀特性等对贯入深度的影响，进而提出砂土海床海底管道贯入深度的预测公式，从而为砂土海床海底管道稳定性分析提供基础。

1 砂土海床海底管道贯入的CEL模型

在风浪流及自重荷载等作用下，海底管道贯入砂土海床，挤压管道周围土体致其向两侧流动，即海底管道贯入砂土海床是一个典型的大变形问题。CEL方法结合了拉格朗日法和欧拉法的优势，在小变形区域采用拉格朗日单元，在大变形区域采用欧拉单元，能够很好地模拟岩土工程中的大变形问题，故本文采用CEL方法模拟海底管道贯入砂土海床过程。

1.1 CEL模型

在ABAQUS软件下建立海底管道贯入砂土海床的CEL模型。海底管道通常为钢制，模量大，变形微小，本文将管道视为刚体，使用拉格朗日单元进行模拟，管道直径D为0.5 m；海床砂土在管道贯入过程中发生流动，采用欧拉单元模拟，选用Mohr-Coulomb本构模型，根据海床砂土常见密度、内摩擦角、剪胀角和弹性模型范围进行土体参数的选取[25-26]，其中土体密度ρ为1 600 kg/m3，内摩擦角φ为39°，剪胀角ψ为15°，弹性模量E为30 MPa。为避免计算收敛问题，砂土取一小的黏聚力0.1 Pa。

本文计算模型为三维模型。砂土宽度(x轴)为10D，高度(z轴)为8D，长度方向(y轴)设定为0.1 m。在土体上方建立1D高度无材料填充的欧拉单元，允许土体自由隆起，模拟海底管道贯入过程中海床的变形过程。为确保计算结果精度，在管-土接触区域宽度3D、高度2D范围内进行网格加密，经过反复试算，加密区域网格尺寸为1/40D，所建CEL模型如图1所示。

图1 CEL模型Fig.1 CEL model

管-土之间的接触面法向为硬接触，切向为库仑摩擦，摩擦系数为1.0，即管-土接触完全粗糙。土体模型的左右边界为水平方向约束，底部边界为竖直方向约束。

在有限元计算中，先对土体进行地应力平衡计算，然后管道竖向贯入，贯入速度v=0.1 m/s，管道贯入0.5D时停止贯入，通过位移加载的方式模拟海底管道在风浪流及自重等荷载作用下贯入砂土海床的过程。

1.2 模型验证

为验证本文所建有限元数值模型的正确性，将CEL模拟结果与DNV-RP-F114规范计算结果进行对比。DNV-RP-F114规范中管道在砂土海床贯入的竖向抗力V计算公式为[24]

(1)

式中：γ′为土体有效重度；Nγ，Nq为土体承载力系数；B为管-土接触宽度；dq为影响深度效应的因素；z0为修正的管道嵌入深度。

承载力系数Nq计算公式为

Nq=eπtan φtan2(45+φ/2)，

(2)

式中φ为土体内摩擦角。

承载力系数Nγ分别采用HANSEN[27]和VESIC[28]地基极限承载力系数，其中HANSEN地基极限承载力系数Nγ为[27]

Nγ=1.5(Nq-1)tanφ。

(3)

VESIC地基极限承载力系数Nγ为[28]

Nγ=2(Nq+1)tanφ。

(4)

由式(2)—式(4)可见，DNV-RP-F114规范中竖向抗力仅与砂土的内摩擦角有关。B，z0，dq计算方法参见DNV-RP-F114规范。

本文CEL模拟结果与DNV-RP-F114规范计算结果对比如图2所示。为便于结果的表示，参照VERLEY等[21]的方法将贯入阻力归一化处理。图2中竖坐标为w/D，其中w为管道贯入深度，横坐标为归一化贯入阻力V/(γD2)，其中γ为土体重度。由图2可知，CEL模拟结果的贯入阻力随贯入深度增加而增大，在贯入的开始阶段，贯入阻力增加较为缓慢，随着贯入深度增加，贯入阻力增长变快，这与DNV规范计算结果规律一致。从图2还可以看出，w在0～0.1D范围内CEL模拟结果与Nγ取式(4)的DNV规范计算结果基本一致，w在0.1D～0.5D范围内CEL模拟结果与DNV规范Nγ取式(3)时计算结果基本吻合，本文CEL模拟结果整体位于DNV规范计算结果区间内，这说明本文建立的砂土海床海底贯入的CEL模型是合理的。

图2 CEL模拟结果验证 Fig.2 Verification of CEL simulation results

2 砂土海床海底管道贯入深度影响因素分析

影响砂土海床海底管道贯入深度的可能因素包括管-土界面特性、土体强度、剪胀特性和弹性模量，本文以上文所述有限元模型作为基本算例，分析管-土界面摩擦系数、砂土内摩擦角和剪胀角及砂土弹性模量对砂土海床海底管道贯入深度的影响规律。

2.1 管-土界面摩擦系数的影响

管-土界面摩擦系数α取0时，管土之间为光滑接触；管-土界面摩擦系数α取1.0时，管土之间为完全粗糙。本文α分别取为0，0.25，0.5，0.75和1.0，利用CEL模型计算海底管道贯入的贯入阻力。图3为不同α下的贯入深度与贯入阻力关系图。从图3可知，海底管道贯入深度为0.5D，α=0时归一化贯入阻力为15.96，α分别为0.25，0.5，0.75和1.0时对应的归一化贯入阻力为24.57，30.34，34.15和36.74，与α=0时归一化贯入阻力相比分别增加了53.95%，90.1%，113.97%和130.2%。由此可以看出，管-土界面摩擦系数对砂土海床海底管道贯入阻力有很大影响，海底管道在贯入相同深度时，管-土界面摩擦系数越大，相应的贯入阻力越大。

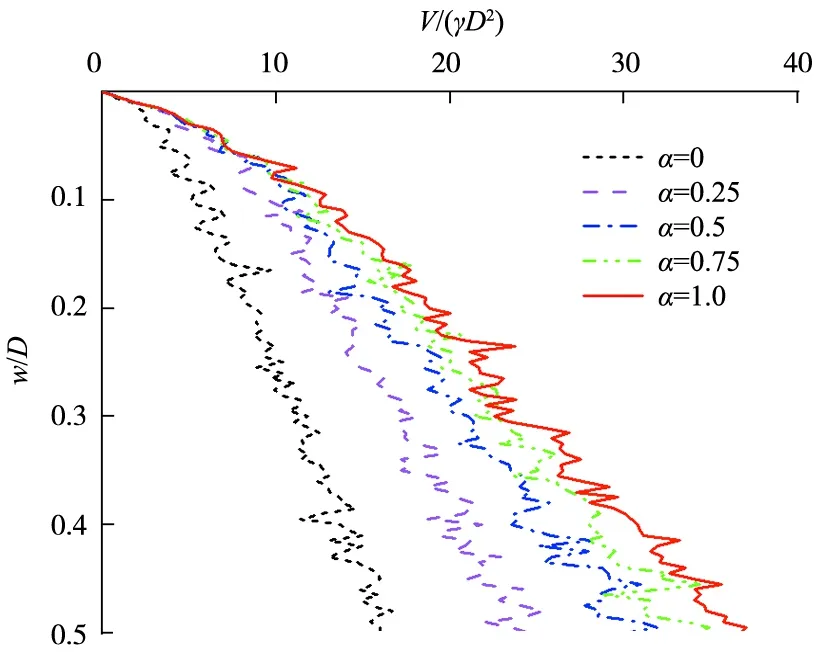
图3 不同管-土界面摩擦系数下的模拟结果 Fig.3 Simulation results under different friction coefficients of pipe-soil interface

图4为管道贯入深度0.5D、管-土界面摩擦系数分别为0和1.0时对应的管道周围砂土速度矢量图。由图4可以看出，土体的破坏区域总体表现为自管道底部向两侧回转，形成类楔形破坏区，在管道两侧形成隆起，海床土体形成了连续的滑动面并自管道底部延伸到海床表面，土体破坏形式表现为整体剪切破坏。对比图4 a)和图4 b)可以看出，管-土界面摩擦系数不同时，砂土的流动状态及影响区域存在差异。如图4 a)所示，当管-土界面完全光滑时，管土之间无摩擦，管道向下贯入时管道正下方的土体表现为沿管道向管道两侧流动。由图4 b)可以看出，管-土界面完全粗糙时，管土之间存在摩擦，管道向下贯入时，管道正下方土体在管土间摩擦力的作用下会产生向下的运动，管-土接触面特性通过管-土间摩擦影响海底管道贯入时土体的流动。同时可以发现，当管-土接触完全光滑(α=0)时，海床隆起的高度约为0.53D，影响深度约为0.82D，影响宽度约为2.15D；而管-土接触完全粗糙(α=1.0)时，海床隆起高度约为0.37D，影响深度约为1.38D，影响宽度约为3.15D，相比管道光滑时土体影响区域更大，这导致管-土界面摩擦系数增大后，贯入阻力增大。

图4 不同摩擦系数下的土体速度矢量图(w/D=0.5)Fig.4 Soil velocity vector diagram under different friction coefficients (w/D=0.5)

2.2 内摩擦角的影响

海床砂土常见的内摩擦角φ范围为30°～40°，本文取φ分别为31°，33°，35°，37°和39°，开展海底管道贯入数值模拟，获得管道贯入深度与贯入阻力之间的关系如图5所示。由图5可知，当贯入深度为0.5D，φ为31°时，归一化贯入阻力为15.74，当φ为33°，35°，37°和39°时，对应的归一化贯入阻力分别为19.79，23.62，29.40和36.74，相比于内摩擦角φ=31°的工况分别增加了25.73%，50.06%，86.79%和133.42%，这说明内摩擦角对管道贯入阻力有很大影响，当贯入深度相同时，砂土内摩擦角越大，管道贯入阻力越大。

图5 不同内摩擦角下的模拟结果Fig.5 Simulation results under different friction angles

图6为管道贯入深度w=0.5D、土体φ分别为31°和39°所对应的管道周围砂土速度矢量图。由图6可以看出，内摩擦角不同时，海床土体均呈现明显的整体剪切破坏特征。对比图6 a)和图6 b)可以发现，在φ为31°和39°时，砂土影响深度分别约为1.13D和1.38D，内摩擦角越大，影响深度越大，这主要是由于内摩擦角越大，土颗粒之间表面摩擦力越大，在管道贯入过程中，砂土颗粒间存在摩擦的同时也存在相对滑动，当颗粒间摩擦越大时，相对滑动越难发生，砂土颗粒受到管道挤压时，更易向下运动。同时，内摩擦角越大，土颗粒之间嵌入和联锁作用产生的咬合力也更强，这导致内摩擦角增大后，贯入阻力增大。

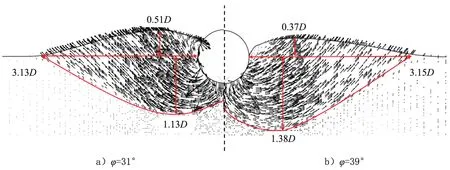
图6 不同内摩擦角下的土体速度矢量图(w/D=0.5)Fig.6 Soil velocity vector diagram under different friction angles (w/D=0.5)

2.3 剪胀角的影响

砂土的剪胀角与松密程度有关，一般密砂剪胀角可取15°，松砂剪胀角可小于10°，本文取剪胀角ψ分别为9°，11°，13°，15°和17°，开展砂土海床海底管道贯入的CEL模拟，获得管道深度与贯入阻力之间的关系如图7所示。由图7可知，贯入深度为0.5D，ψ=9°时归一化贯入阻力为29.50，ψ分别为11°，13°，15°和17°时对应的归一化贯入阻力为31.91，33.98，36.33和39.00，与ψ=9°时归一化贯入阻力相比分别增加了8.17%，15.19%，23.15%和32.2%，这说明剪胀角同样也会对海底管道在砂土海床的贯入阻力产生影响，当贯入深度相同、剪胀角不同时，贯入阻力随着剪胀角的增大而增大。

图7 不同剪胀角下的模拟结果Fig.7 Simulation results under different dilation angles

图8为管道贯入深度为0.5D、土体剪胀角ψ=9°和15°时分别对应的管道周围砂土速度矢量图。由图8可以看出，剪胀角不同时，海床土体破坏形式均表现为整体剪切破坏。对比图8 a)和图8 b)可以看出，当土体的剪胀角越大时，土体隆起高度及影响的深度和宽度范围越大，这主要是因为随着剪胀角增大，土体在受到管道的贯入之后产生的塑性体应变和塑性区范围增大，剪胀角越大土体影响区域越大，这导致剪胀角增大后，贯入阻力增大。

图8 不同剪胀角下的土体速度矢量图(w/D=0.5)Fig.8 Soil velocity vector diagram under different dilation angles (w/D=0.5)

2.4 弹性模量的影响

选取5种不同的弹性模量，分别为E=10，15，20，25，30 MPa，通过有限元计算得到如图9所示的贯入深度与贯入阻力关系图。由图9中可以看出，5条曲线基本重合，即弹性模量不同时贯入阻力近似相同，从而可以说明弹性模量E的变化对于贯入阻力来说没有显著影响。

图9 不同弹性模量下的模拟结果Fig.9 Simulation results under different elastic modulus

3 贯入深度预测的经验公式

为预测砂土海床海底管道贯入深度，提出海底管道贯入砂土海床贯入深度的经验公式。由分析可知，海底管道在砂土海床的贯入过程受管-土界面摩擦系数、砂土内摩擦角和剪胀角的影响较大，故本文提出考虑上述因素的海底管道贯入深度预测经验公式。

3.1 经验公式的提出

从以上数值模拟结果可以看出，当贯入阻力一定时，贯入深度受管-土界面摩擦系数、砂土内摩擦角、剪胀角的共同影响，贯入阻力分别随管-土界面摩擦系数、砂土内摩擦角、剪胀角和贯入深度的增加而增大，贯入阻力与管-土界面摩擦系数、砂土内摩擦角、剪胀角和贯入深度呈正相关关系。此外由数值模拟结果发现，内摩擦角为33°，35°，37°和39°时对应的归一化贯入阻力相比于内摩擦角31°的归一化贯入阻力分别增加了25.73%，50.06%，86.79%和133.42%，其增幅在3个影响因素中最大，因此可说明在一定范围内，内摩擦角对于贯入阻力影响最大。

选取的4个无量纲量分别为

(5)

归一化贯入阻力可以表示为

(6)

各无量纲量与归一化贯入阻力关系如图10所示，可以发现归一化贯入阻力与4个无量纲量近似呈幂函数变化。幂指数函数可表示为

(7)

式中：a，b为拟合系数。

对各无量纲量及对应的归一化贯入阻力采用式(7)进行拟合，拟合结果如图10所示。由图10可知，采用幂指数函数对归一化贯入阻力与4个无量纲量进行拟合，相关系数R2平均值为0.991，拟合结果较好，说明归一化贯入阻力随各参数变量的变化近似呈幂函数规律。

图10 各无量纲量与归一化阻力关系图Fig.10 Relationship between each dimensionless quantity and normalized resistance

在图10基础上，建立归一化贯入阻力与4个无量纲量之间的函数关系即非线性乘法模型：

(8)

式中：β，x1，x2，x3，x4为拟合系数。

取自然对数，可得：

(9)

利用LINEST函数，进行多元线性回归计算，然后得到：

β=2 966.337，x1=0.332，x2=3.676，x3=0.513，x4=0.671。

(10)

本文分别研究了管-土界面摩擦系数α范围为0～1，砂土内摩擦角φ范围为31°～39°，剪胀角ψ范围为9°～17°下的海底管道在砂土海床深度范围为0～0.5D的贯入阻力随贯入深度的变化关系，基于数值模拟结果，最终得出贯入深度的预测经验公式：

(11)

公式的适用范围为

(12)

3.2 经验公式验证

为验证经验公式的准确性，将ZHAO等[22]关于管道在砂土贯入的离心机试验土体参数代入至本文经验公式中，与其离心机试验结果进行对比验证，对比结果如图11所示。由图11可以看出，离心机试验数据具有较大的波动性，但整体呈现出贯入阻力随贯入深度的增加而增大的趋势，与经验公式结果规律一致。经验公式计算结果位于离心机试验结果波动范围之间，与离心机试验结果具有良好的相关性，这说明本文所提出的预测海底管道在砂土海床贯入深度的经验公式是合理的。

图11 经验公式验证Fig.11 Verification of empirical formula

3.3 经验公式与DNV规范对比

为验证拟合公式的准确性，在既有模型参数的基础上重新选取了6种不同工况进行计算，计算工况如表1所示。将CEL模拟结果分别与DNV-RP-F114规范计算结果和所提出的经验公式计算结果进行对比，结果如图12所示。

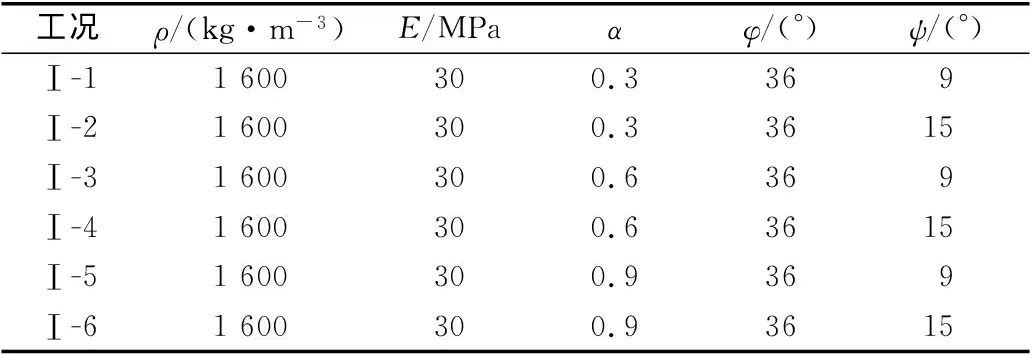
表1 计算工况

图12 经验公式与DNV规范对比结果Fig.12 Comparison results between empirical formula and DNV specification

图12 a)为CEL模拟结果与DNV-RP-F114规范计算结果对比，由图12 a)可以看出，工况Ⅰ-4～Ⅰ-6的CEL模拟结果位于DNV-RP-F114规范计算结果区间，而工况Ⅰ-1～Ⅰ-3的CEL模拟结果与DNV-RP-F114规范计算结果相关性较差，说明DNV-RP-F114规范只考虑砂土内摩擦角的影响，虽在一定程度上可预测海底管道在砂土海床的贯入深度，但具有一定的局限性。图12 b)为CEL模拟结果与本文所得经验公式计算结果对比，如图12 b)所示，CEL模拟结果与经验公式计算结果相差较小，拟合效果较好，由此说明，本文基于管-土界面摩擦系数、砂土内摩擦角、剪胀角所提出的砂土海床海底管道贯入深度预测经验公式适用性更强，所提出的经验公式在一定条件范围内能够较好地预测海底管道在砂土海床的贯入深度。