电动汽车非对称混合磁极永磁电机优化与分析

刘楷文，史立伟，王文强，刘政委，李法成

(山东理工大学电动汽车智能化动力集成技术国家地方联合工程研究中心，山东淄博 255049)

环境污染以及石油消耗等问题日益严峻，发展电动汽车成为环境保护的一项重要举措[1-2]。电机作为电动汽车上的核心部件，对于电动汽车的性能有决定性的作用[3-5]。为满足电动汽车驱动电机所需要的高性能要求，采用稀土材料的永磁电机在电动汽车上得到了广泛的应用[6-8]。

中国稀土储量全球第一，约占全球稀土总储量的37%，同时，中国也是世界上最大的稀土出口国，承担全球约75%以上的稀土供应。中国即将面临因稀土材料开采过量而导致的资源紧缺困境。稀土材料的价格波动以及不稳定的供应链也极大地增加了稀土永磁电机的制造成本，限制了稀土永磁电机的发展[9-10]。

近年来，越来越多的学者开始寻找可以替代稀土材料的其他材料，并研究低成本的永磁电机，而价格低廉的铁氧体成为了替代稀土材料的首选。但单纯的铁氧体永磁电机满足不了电动汽车的动力需求[11-12]，国内外学者开始将目光转向少稀土永磁电机。ZHAO等[13]提出了一种轴向磁通盘式转子永磁电机以提高非稀土永磁电机的性能；ZENG等[14]提出了非稀土材料与稀土材料组成串联磁路的少稀土电机，并在转子铁心开辅助槽，以此保持电机的性能；文献[15]和[16]分析了电机定子齿齿肩形状以及定子齿宽度对电机性能的影响，文献[17]—文献[19]分别提出了3种不同结构的多层磁钢，利用更大的磁阻转矩降低电机的转矩脉动和齿槽转矩，以提高电机性能，但增大了永磁体的用量和电机的制作难度。REN[20]提出采用圆柱型转子上半部与下半部错位一定角度的特殊结构，能够降低电机的齿槽转矩与转矩脉动。文献[21]和[22]分别提出诸如单参数扫描法、响应面法以及田口算法等优化算法，但这些优化方法在使用时有诸多限制，并且不能够确保精度，也保证不了优化结果的最优性。

目前，少稀土电机成为研究的热点，但输出转矩低是少稀土电机不可避免的问题，仅通过增加非稀土材料的体积来提高少稀土电机的性能有一定的局限性。同时，传统永磁电机存在的转矩脉动和齿槽转矩过高等问题也有待解决。

为减少稀土材料的使用量并提高电机的电磁性能，本文提出一种新型非对称混合磁极永磁电机结构，建立一种基于参数分层设计的响应面法与MOGA-Ⅱ相结合的多目标优化方法。该优化方法在考虑参数交叉影响和确保精确度的同时，减少优化次数，并根据优化结果确定电机的结构参数。

1 结构分析与设计

1.1 电机拓扑结构

本文给出一种新型非对称混合磁极永磁电机转子，其拓扑结构示意图如图1 b)所示，图1 a)为传统V型结构电机转子拓扑结构图。新型非对称混合磁极永磁电机转子磁极采用稀土材料钕铁硼和非稀土材料铁氧体2种永磁材料作为励磁源共同励磁。钕铁硼1、钕铁硼2、钕铁硼3和钕铁硼4的面积各不相同，且与磁极轴线的夹角也各不相同(α≠β≠γ≠δ)，铁氧体1与铁氧体2的宽度不相同(Wpm1≠Wpm2)。

图1 永磁电机转子拓扑结构Fig.1 Topological structure of permanent magnet motor rotor

采用非对称混合磁极结构能够从2个方面提高电机的电磁性能：首先，经过优化后的不等极弧夹角可以消除转子磁动势中的奇次谐波，从而抑制转矩脉动；其次，稀土材料钕铁硼和非稀土材料铁氧体相结合组成的混合结构，能够增加电机磁路内的有效磁通。

1.2 电机有效磁通分析

对比分析新型非对称混合磁极永磁电机和传统V型结构电机的磁通路径，传统V型结构电机的有效磁通路径为单一路径，而新型非对称混合磁极永磁电机每一对磁极之间的总有效磁通路径由2条有效磁通路径并联组成，分别由钕铁硼1、钕铁硼3和铁氧体2共同提供。利用等效磁路法对比分析2种电机的磁通路径，分别建立传统V型结构电机和新型非对称混合磁极永磁电机的等效磁路模型如图2所示。

图2 电机等效磁路Fig.2 Equivalent magnetic circuit of the motor

在图2中，FL，FS和FT分别为钕铁硼1、钕铁硼3和铁氧体2所提供的磁通势；Fd为电枢反应的直轴分量；GmL与GmS分别为钕铁硼1与钕铁硼3的等效内磁导；GmT为铁氧体2的等效内磁导；2Gmμ1与2Gmμ2为钕铁硼1和钕铁硼3与转子铁芯之间的磁导；2Gmμ3为铁氧体2与转子铁芯之间的磁导；GLL和GLS分别为钕铁硼1和钕铁硼3的漏磁导；Gg为定子铁芯与转子铁芯之间的气隙磁导；GT与GY分别为定子铁芯齿部和轭部的磁导；Gr1，Gr2和Gr3分别为钕铁硼1、钕铁硼2和铁氧体2外侧转子铁芯的磁导；Grp1为钕铁硼1与钕铁硼3之间转子铁芯的磁导；Grp2为钕铁硼1与铁氧体2之间转子铁芯的磁导；Φm为磁路中所有永磁体提供的总磁通；Φme为磁路中的有效磁通，ΦLL与ΦLS分别为钕铁硼1与钕铁硼3的端部漏磁通。

通过对2种不同结构电机的等效磁路对比分析，可以发现新型非对称混合磁极永磁电机的磁路中新增加了Φm1和Φm2，Gr1与Gr2，Gr3并联，令G′为Gr2，Grp1，2Gmμ2，GmS和GLS的总磁导，G″为Gr3，Grp2，2Gmμ3和GmT的总磁导，由叠加原理可知：

(1)

(2)

分析得Gr1与G′，G″并联之后的总磁导Ge满足:

(3)

则：

Ge>max{Gr1,G′,G″}。

(4)

由式(1)、式(2)和式(4)可以看出，相比于传统V型结构电机，本文所提出的新型非对称混合磁极永磁电机磁路内的总磁导高于传统V型结构电机磁路内的总磁导，在总磁动势不变的情况下，磁路内的有效磁通增加。

2 电机参数优化

2.1 确定优化目标及设计参数

以转矩脉动Trip、齿槽转矩Tcog以及空载反电势谐波畸变率(THD)为综合优化目标，对电机转子结构参数(见表1)进行优化。本文建立一种响应面法与MOGA-Ⅱ相结合的多目标优化方法，其流程如图3所示。

表1 电机结构主要优化参数及变化范围

图3 多目标优化流程Fig.3 Multi-objective optimization process

2.2 设计参数灵敏度

参数灵敏度是优化参数对于优化目标的影响程度。引入灵敏度指数S(xi)来表示优化参数对优化目标的影响程度，灵敏度公式如下：

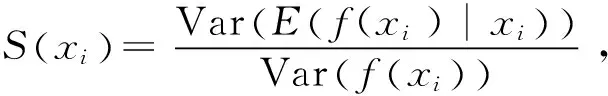
(5)

式中：Var(E(f(xi)|xi))表示E(f(xi)|xi)的方差；Var(f(xi))表示f(xi)的方差；E(f(xi)|xi)表示f(xi)关于xi的平均值。

式(5)只能够表示单一参数对优化目标的影响，因此，选用G(xi)代表综合参数灵敏度，确定各个优化参数对优化目标的综合影响程度：

G(xi)=λ1|Scog(xi)|+λ2|Srip(xi)|+λ3|STHD(xi)|，

(6)

式中：Scog(xi)为优化参数对齿槽转矩的灵敏度；Srip(xi)为优化参数对转矩脉动的灵敏度；STHD(xi)为优化参数对空载反电势谐波畸变率的灵敏度；λ1，λ2和λ3分为齿槽转矩、转矩脉动以及空载反电势谐波畸变率的权重系数，各权重系数满足λ1+λ2+λ3=1，将齿槽转矩、转矩脉动与反电势波形畸变率的权重系数分别设置为0.6，0.2与0.2。

根据表2所得到的数据，可以将参数分成2层，第1层为主要影响因素，第2层为次要影响因素，分层结果如表3所示。

表2 优化参数对优化目标的灵敏度 分析结果

表3 优化参数分层结果

2.3 构建RSM模型

根据构建RSM模型中BBD和CCD的方法设计原则，建立正交矩阵并通过有限元分析各个水平值下优化目标的响应值。对试验结果的响应值进行多元二次回归拟合，拟合多项式如式(7)所示。

(7)

式中：G(t)为响应值；a0，ai和aii为回归系数；ti和tj为2个不同的优化变量；ε为拟合误差。

第1层优化中含有4个优化变量，一般需要44=256次试验，才可分析出各个变量之间的相互作用，找出最优的组合。将每个因子的3个级别定义为-1，0和+1。将0定位中心点，-1和+1为相对高低值。各设计变量水平值以及自编码如表4所示。

表4 优化变量水平值

2.4 基于BBD的第1层优化

根据四水平三因素试验设计原则，建立BBD的正交试验组合。通过29组仿真得到关于齿槽转矩(Tcog)、转矩脉动(Trip)以及THD的响应。其响应组合以及结果如表5所示。

表5 BBD响应组合及结果

2.5 基于CCD的第2层优化

根据二水平试验设计原则，建立CCD的正交试验组合。通过13组仿真得到过于齿槽转矩(Tcog)、转矩脉动(Trip)以及THD的响应。其响应组合以及结果如表6所示。

表6 CCD响应组合及结果

2.6 基于MOGA-Ⅱ的优化

为了更加准确寻找第1层参数的全局最优解，对RSM的二阶数学模型采用MOGA-Ⅱ算法进行求解。MOGA-Ⅱ是一种多目标遗传算法，对于多目标优化问题的最优解不是单一的，而是一组，这一组最优解称为Pareto解集。在齿槽转矩(Tcog)、转矩脉动(Trip)以及空载反电势谐波畸变率(THD)为优化目标的基础上，加入平均转矩的约束条件(Tavg≥15.2 N·m)，使得所求解集更加贴近设计要求，根据优化目标综合考虑，在Pareto解集中选择一个最优解，得到的优化结果如图4所示。

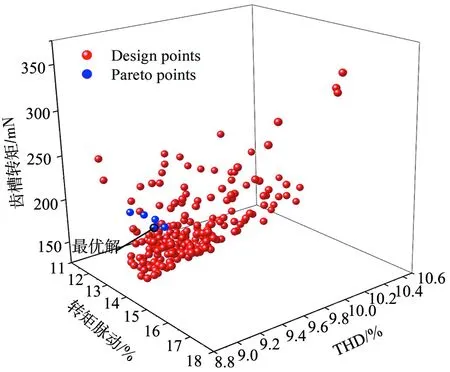
图4 第1层优化结果的Pareto解与设计解Fig.4 Pareto solution and design solution of the first layer optimization results

图4给出了3个优化目标的优化结果，图中设计解集满足设计要求，Pareto解集满足约束条件要求。从Pareto解集中选择一个最优解，将其对应的优化变量值作为最终的优化值，最终结果如表7所示。

表7 优化变量最终结果

表8为新型非对称混合磁极永磁电机与传统V型结构电机所用永磁材料用量对比结果，在保证新型非对称混合磁极永磁电机的输出转矩不低于传统V型结构电机输出转矩的前提下，非对称混合磁极永磁电机的稀土材料的使用量相较于传统V型结构电机降低了14.3%。

表8 永磁材料用量对比结果

3 电磁性能分析

3.1 电机结构参数

利用电磁场有限元分析新型非对称混合磁极永磁电机电磁场，电机尺寸数据如表9所示，通过建立2种结构的永磁电机模型，对比分析新型非对称混合磁极永磁电机与传统V型结构电机的电机性能。

表9 电机结构主要参数

3.2 电磁转矩分析

转矩脉动为转矩的峰-峰值与平均转矩的比值，可以用来衡量电机输出转矩波动的大小，如式(8)所示。

(8)

式中：Trip，Tmax，Tmin和Tavg分别为电机的转矩脉动和输出转矩的最大值、最小值以及平均值。

当电枢电流通入87 A的额定三相电流时，额定负载下传统V型结构电机和新型非对称混合磁极永磁电机的输出转矩性能结果如图5所示。

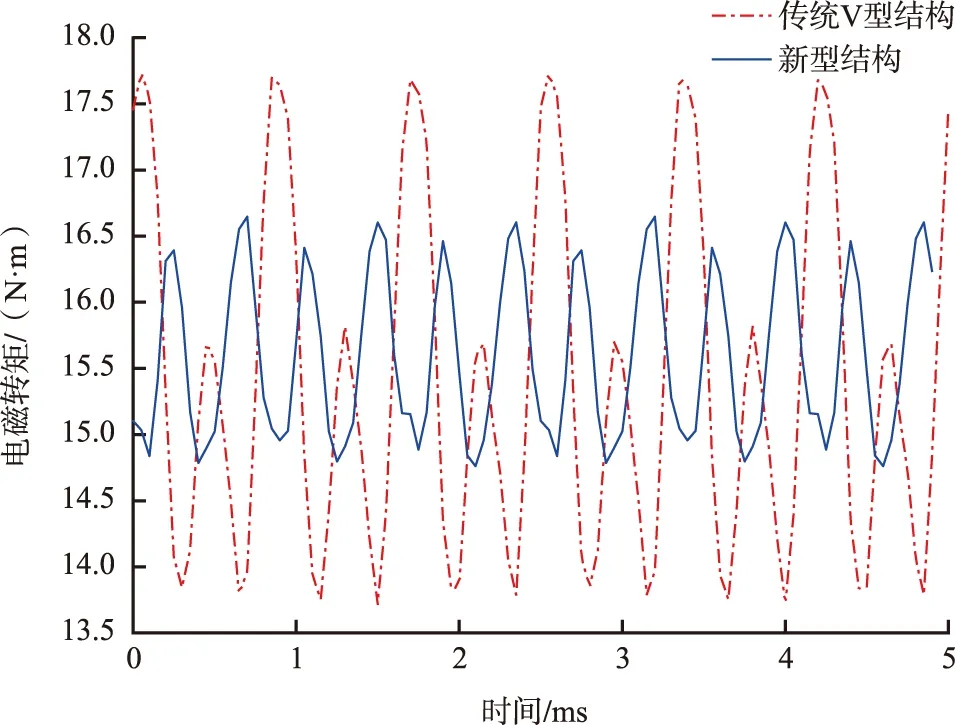
图5 永磁电机输出转矩分析 Fig.5 Output torque analysis of permanent magnet motor

从图5可以看出，在保持电机平均输出转矩基本不变的前提下，传统V型结构电机相比于新型非对称混合磁极永磁电机转矩脉动由26%降低至12%。

3.3 齿槽转矩分析

传统V型结构电机和新型非对称混合磁极永磁电机的齿槽转矩对比结果如图6所示。传统V型结构电机的齿槽转矩波动较大，齿槽转矩峰-峰值为1.1 N·m。新型非对称混合磁极永磁电机的齿槽转矩峰-峰值为0.32 N·m，相比传统V型结构电机齿槽转矩峰-峰值削减了71%。

图6 永磁电机齿槽转矩分析 Fig.6 Cogging torque analysis of permanent magnet motor

3.4 空载反电势分析

根据有限元分析得到电机在额定转速3 000 r/min下的空载反电势，结果如图7所示。由图7 a)可以看出，新型非对称混合磁极永磁电机的空载反电势峰值要大于传统V型结构电机的空载反电势峰值，电势峰值提高了23.1%。对空载反电势进行傅里叶分析，结果如图7 b)所示，由图7 b)可以看出，新型非对称混合磁极永磁电机的空载反电势基波幅值要大于传统V型结构电机，新型非对称混合磁极永磁电机波形畸变率相对于传统V型结构电机降低了10%。本文所提出的新型非对称混合磁极永磁电机能够有效减少空载反电势的5次谐波、7次谐波和9次谐波含量，提高了电机的性能。

图7 永磁电机空载反电势与谐波分析Fig.7 No-load back potential and harmonic analysis of permanent magnetmotor

3.5 退磁性能分析

铁氧体的矫顽力过低，在过大的电枢电流下铁氧体会发生不可逆的退磁，所以对铁氧体的退磁分析也是辨别电机性能好坏的重要部分。该电机在额定负载状态和过载状态下的退磁分析结果如图8所示。可以看出，新型非对称混合磁极永磁电机在额定负载状态下没有发生退磁现象，在过载状态下铁氧体的两侧边角出现很小的不可逆退磁区域，并不影响电机性能。这也证明了新型非对称混合磁极永磁电机的抗退磁性能良好。

图8 退磁分析Fig.8 Demagnetization analysis

3.6 电机效率分析

图9给出非对称混合磁极永磁电机的效率Map图。由图9可知，非对称混合磁极永磁电机可在较宽调速范围内保持高效率运行，该仿真结果验证了本文所提出的新型电机用作电动汽车驱动电机的可行性。

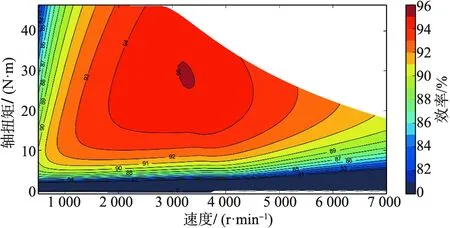
图9 电机效率Map图Fig.9 Motor efficiency Map

4 实验验证

为了能够验证所提出的新型非对称混合磁极永磁电机的可行性，将优化后的最终尺寸结构电机进行加工，制作了额定功率为5 kW，额定转速为3 000 r/min的三相8极48槽的样机，样机定子以及转子结构如图10 a)、b)所示。图10 c)、图10 d)和图10 e)分别为齿槽转矩测试仪、测功机实验台和对拖实验台。

图10 样机及实验平台Fig.10 Prototype and experimental platform

本次测试使用测功机实验台来测试电机的机械特性，如图11所示，新型非对称混合磁极永磁电机的最高转速为5 000 r/min，在满载状态下，最大转矩为46.8 N·m，最大效率高于90%。

图11 样机特性曲线Fig.11 Prototype characteristic curve

齿槽转矩经过转矩测试仪测试结果如图12所示，齿槽转矩的峰-峰值为0.35 N·m，略高于有限元仿真的预测值，验证了新型转子结构的合理性。

图12 样机齿槽转矩Fig.12 Prototype gear cogging torque

多数情况下，永磁电机既可以作为发电机又可以作为电动机运行。为了更清晰地观测到空载反电势波形，实测了样机在额定转速为3 000 r /min下的三相空载反电势，如图13 a)所示。对实测的反电势波形进行傅里叶分解，结果如图13 b)所示。

图13 样机空载反电势波形Fig.13 Prototype no-load back potential waveform

5 结 论

为改善永磁电机的电机性能，本文提出一种新型非对称混合磁极永磁电机结构，建立了磁路模型，结合有限元分析和样机实验，对定子为48槽下的非对称混合磁极永磁电机与传统V型结构电机进行对比，验证了本方案理论分析的正确性，得到以下结论：

1)对新型非对称混合磁极结构电机与传统V型结构电机的分析结果表明，新型非对称混合磁极永磁电机相比传统V型结构电机的转矩脉动、齿槽转矩以及空载反电势波形畸变率分别降低了14%，71%和10%；2)新型非对称混合磁极永磁电机将少稀土材料与非对称结构相结合，在保证平均输出转矩性能的前提下，使稀土材料的使用量降低了14.3%；3)相比普通的遗传算法和单参数优化方法结合的方式，采用一种基于参数分层设计的响应面法与MOGA-Ⅱ相结合的多目标优化方法不仅可以充分考虑到参数交叉对结果的影响，还能够在确保精确度的同时，减少优化时间。

本文不足之处在于虽然通过多目标分层优化设计确定了电机参数的最优解，但还需要制定合适的控制策略，因此未来还需对电机的控制策略进行深入研究，以改善电机的整体性能。