小角度斜流下导管桨/螺旋桨尾流场数值分析

2022-09-11张嶔何聪许情赵昌宇郭子康中国海洋大学工程学院山东青岛266100

哈尔滨工程大学学报 2022年8期

张嶔，何聪，许情，赵昌宇，郭子康(中国海洋大学工程学院, 山东青岛 266100)

作为轨迹与形态操纵的主动控制装置，导管桨和螺旋桨越来越多地应用于船舶、水下航行器及海洋平台动力定位系统中，其研究也呈现出不断发展的趋势。为了保证导管桨和螺旋桨在各种工况下的平稳运行，需要对导管桨和螺旋桨的性能进行详细的分析。导管桨和螺旋桨水动力性能及流场特性分析主要集中于船舶在直航的设计要求条件下进行，在其使用寿命期间，船舶可能会经历不同的非设计情况，如操纵以一角度行驶，这完全改变了螺旋桨或导管桨的工作状态。在这些情况下，由于船体、导管桨/螺旋桨和舵之间的相互作用，导管桨/螺旋桨相对于直行运动期间所产生的流场形态会发生改变，产生复杂的流场现象，可能会对船舶的动态响应产生较大影响。开展斜流情况下导管桨/螺旋桨的尾流场特性研究对于船舶、水下航行器等领域具有重大意义。除物理实验研究外，计算流体力学在船舶螺旋桨分析和设计中的应用也越来越广泛[1]。多参考系方法作为一种准稳态方法，通常用于计算导管螺旋桨的性能，如推力、扭矩和效率[2]。此外，文献[3-5]对带有移动网格的全叶片几何结构进行了工业瞬态滑动界面模拟。对无导管螺旋桨和导管螺旋桨的研究也扩展到了非设计状态。Giulio 等[6-7]基于雷诺平均Navier-Stokes方程解的数值程序在非设计条件下研究了螺旋桨推力、扭矩等敞水性能，结果表明计算敞水性能的结果和试验值吻合良好，但斜流状态下缺乏试验数据，无法进一步的验证。基于计算流体动力学对倾斜条件螺旋桨进行数值模拟，对螺旋桨负载、垂直方向的力和力矩、流场涡结构有显著影响[8-9]。张志荣等[10]运用了数值计算和实验的方法，研究了DTMB 4679在斜流中的水动力性能，结果表明DTMB 4679的流动具有很强的非定常特性。孙聪等[11]进行斜流下导管桨的水动力性能及流场特性数值分析，结果表明设计工况、小斜流角状态下导管桨的推进效率会有小幅提高。邱振良等[12]分析了螺旋桨在斜流下产生的横向力的成因及其对船舶操纵性的影响。Merkle等[13]对一个全方位推进器7°的尾流进行了物理和数值研究，同时对某船用螺旋桨在10°～50°斜流中的性能进行了分析。这些研究表明，横向流动对螺旋桨的流体动力性能具有重大影响。

在斜流条件下，对导管桨/螺旋桨性能的研究逐步完善，但是在一个恒定的进速系数下小倾角的导管桨/螺旋桨尾流场特性的分析研究还较为零碎，本文在原有的的数值方法基础上进一步改进，利用OpenFOAM开源软件并基于带滑移网格的延迟分离涡(delayed detached eddy simulation，DDES)模型对导管桨/螺旋桨在小倾斜角(β=15°、β=30°)下的尾流场特性研究分析导管桨和螺旋桨的优劣。

1 湍流模型数值设置

数值计算采用三维黏性、不可压缩的紊流模型。计算中所用螺旋桨和导管型号分别为5810R和1393，桨模直径D为0.1 m，螺距比为1，其中导管桨模型参照四叶导管桨，由桨毂、四片桨叶、导管以及推杆组成[14]。

1.1 湍流模型

延迟分离涡数值计算模型[15]在近壁面区域采用雷诺平均(Reynolds average navier-stokes，RANS)模型，在保证求解精度的同时减少计算时间，而在尾流区域采用计算精度更高的大涡模拟(large eddy simulation，LES)，因此兼有RANS模型和LES模型的优点，并且在脱体涡模拟方法[16](detached eddy simulation，DES)的基础上解决了由网格密度引起的近壁面处模拟应力耗尽的问题。但考虑到计算时间和计算资源的占用，本文采用先基于多旋转参考系(multiple reference frame，MRF)模型的定常数值模拟计算，再利用定常数值模拟提供的初始化流场信息，进行非定常RANS数值模拟计算直到流场稳定，获得基于Spalart-Allmaras紊流模型的非定常流场结果；最后开启基于DDES模型与滑移网格(arbitrary mesh interface，AMI)相结合的高精度非定常尾涡演化数值模型计算。

1.2 计算域与边界条件

计算域为如图1(a)所示倾斜15°的与导管桨/螺旋桨同轴的圆柱形区域，D为导管桨直径，直径为10D、长度为13D。在来流方向上，入口离桨2.5D，出口离桨10.5D[17-18]。计算域左侧设置为速度入流边界，通过设置入口速度来模拟特定进速系数下的工况，右侧为压力出口边界，圆柱形边界为对称边界。计算域分为旋转域和静止域，其中螺旋桨所在的部分为旋转域，旋转域的侧面与导管桨内侧平行相距3 mm，其余部分划分为静止区域，不同的区域之间通过交界面进行数值交换，如图1(b)所示。其中，U进流速度，β为倾斜角度。

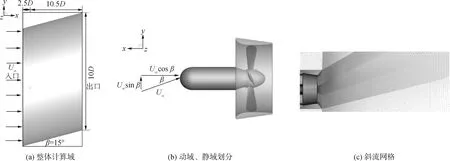
图1 导管桨整体计算域、区域划计算域、区域划分及斜流网格Fig.1 Overall calculation domain, region division and oblique flow grid of ducted propeller

1.3 网格划分与工况设定

计算域使用规则和平滑的纯结构化网格进行离散，对导管桨/螺旋桨表面及周围进行结构化网格划分，对导管桨、桨叶叶梢和导管之间设置为网格加密区域以捕捉叶梢涡的产生。

为了捕捉尾迹的不稳定性流场，对尾迹区域进行了适当的细化。导管桨计算网格总数为3.3×107，螺旋桨计算网格总数为4.2×107。网格适应性分析参见文献[17]。螺旋桨进速系数为：

J=U/nD

(1)

式中n为导管桨转速。

数值模拟工况设定：对导管桨/螺旋桨进速系数J=0.4，转速17.65 rad/min，进流速度Ux为0.706 m/s下倾斜角度β=15°、β=30°的2种工况作非定常验数据吻合较好，只有在系泊条件J=0时，数值模拟的扭矩系数略大于试验结果，结果为试验水槽效应引起，该差异同文献[14]数值模拟结果也是一致的。数值模拟工况设置如表1的所示。

表1 数值模拟工况设置Table 1 Numerical simulation working condition setting

数值模拟计算过程中，非定常数值模拟计算时间步长取1.575×10-5s，旋转一周的物理时间为0.056 7 s，即叶片每旋转30°保存一次，共计转25圈，取15～25圈的数据作后续处理。

2 数值计算结果分析

2.1 定常数值模拟结果验证

导管桨相比无导管螺旋桨多了导管的存在，数值模拟过程比无导管螺旋桨更为复杂，本文首先以导管桨为例，验证数值模型的正确性。

桨的推力系数KT和扭矩系数KQ在导管桨中由螺旋桨推力和导管产生的推力部分组成，分别为：

KT=T/ρn2D5

(2)

KQ=Q/ρn2D5

(3)

将定常数值模拟得到的导管桨推力与扭矩代入式(2)、(3)得到推力系数和扭矩系数，将结果与文献[19]的试验数据进行比较结果表明数值模拟结果与实验数据吻合较好，只有在系泊条件J为0时，由于试验水槽效应，数值模拟的扭矩系数略大于试验结果，该差异同文献[20]数值模拟结果一致。

2.2 非定常数值模拟结果验证

ZHANG等[20]分析了推进器方向速度等值线，从数值模拟可以看出有比较均匀的循环速度分布且与物理实验结果一致。比较x轴(推进器方向)速度沿半径的分布，并对数模多个尾流截面的RANS模拟与粒子图像测速(particle image velocimetry，PIV)数据进行了对比。以定常数值计算结果作为初始流场，选取导管桨进速系数J=0工况进行非定常数值模拟的结果验证。将非定常数值计算得到的yz截面x/D=I位置时均速度场[17]与Cozijn[21]的PIV试验数据对比，结果表明2种非定常模型模拟结果均与试验结果高度一致，但DDES模型在高速区外的过渡区域比RANS模型能更好的捕捉与物理模型试验相似的不稳定尾迹流场细节。说明基于Spalart-Allmaras紊流模型的DDES模型进行非定常数值模拟的准确性且可以更好地展示不稳定尾流场细节。

为了更好地展示非定常数值模型对于尾流场模拟的精确性，对导管桨尾流场沿尾流方向取横截面，将RANS和DDES模型的计算结果[17]与MARIN JIP项目的RANS数值模拟结果[14]和PIV试验结果[16]进行对比。从结果可以看出，忽略本文不考虑在内的推进器手柄对尾流的作用，通过DDES模型对导管桨尾流场的模拟与试验结果能够很好地吻合，可以继续进行后续的分析研究。

2.3 流场特性分析

选取15～25圈内的数据用于流场分析，将每圈叶片旋转至同一相位(如0°、90°、180°、270°)的4个瞬时流场取平均，得到叶片在相同位置的尾流场相位平均值。

图2显示了导管桨/螺旋桨在不同的倾斜角度下相位平均的速度场变化。导管桨和螺旋桨的叶梢处由于叶片周期性的切割，叶梢泄涡和叶梢涡形成了呈锯齿状的高速区。在进度系数J=0.4条件下，随倾斜角度的增加，导管桨高速区相比于螺旋桨不易保持，且由于导管的屏蔽作用，导管螺旋桨的尾流场受斜流的影响较小。而相比导管桨，螺旋桨的高速区普遍比导管桨的强，螺旋桨的高速区宽度更大，并随着随倾斜角度的增加，流场也更为复杂。在倾斜角β=30°时，明显看出其尾涡消散段不再呈现线性变化，在中后期发展段伴随有小角度转折，且其尾流消散段距离比倾角为15°时的短，产生这种现象的原因可能是随着倾角的增加，导管桨尾流场受入流倾角的影响越加明显，且入流倾角的增加有增加导管桨低速区的趋势。

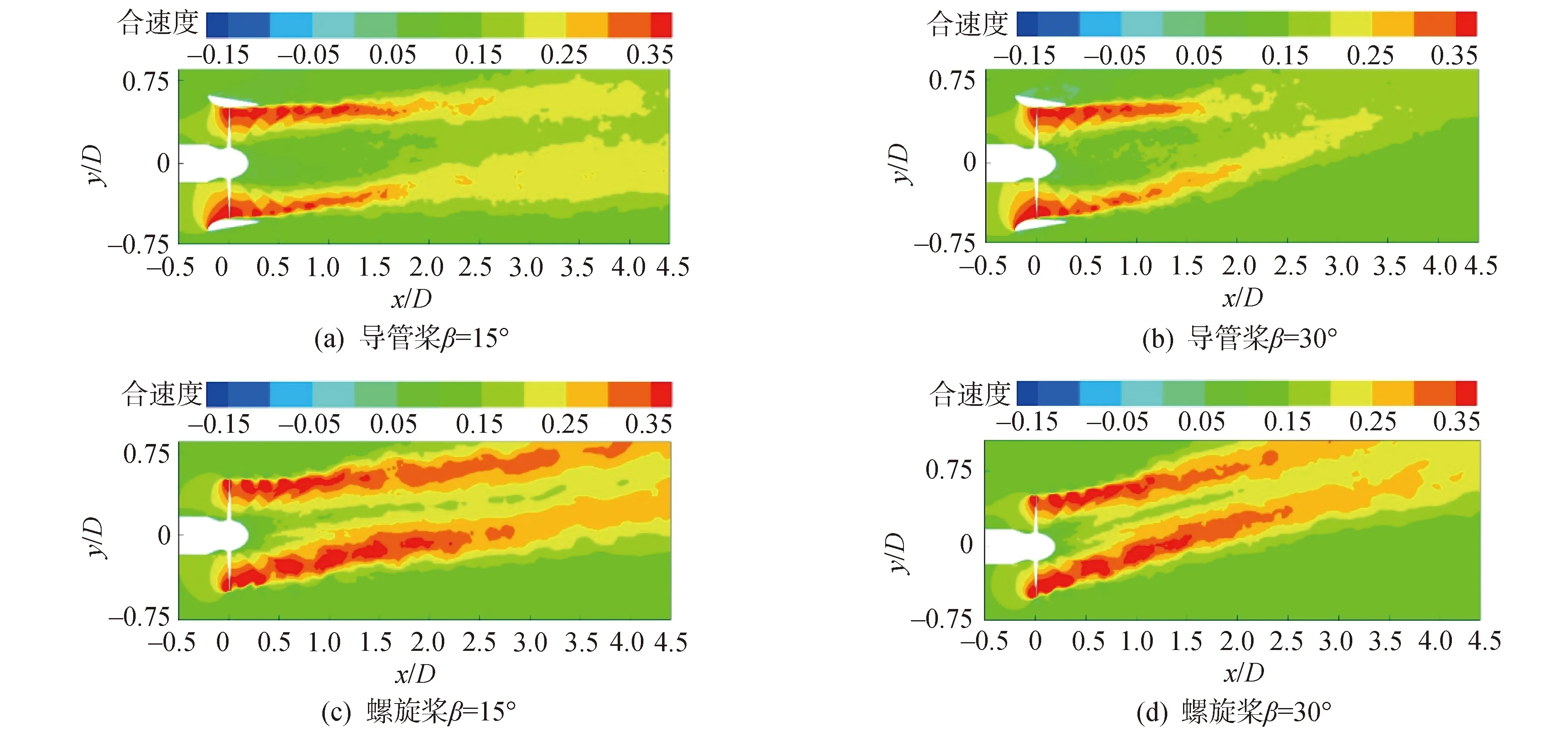
图2 小斜流角度(15°, 30°)导管桨螺旋桨相平均流速对比(Uref无量纲化)Fig.2 Comparison of average velocity of ducted propeller and propeller phase with small oblique flow angle (15°, 30°)，the streamwise velocity is normalized by Uref

图3为导管桨/螺旋桨旋转过程中叶片和代表性叶片截面上形成的相位平均的压力场变化，更好地了解斜流对尾流压力场的影响。由图3可见，导管桨的叶梢泄涡和螺旋桨的叶梢涡形成的涡环低压区清晰可见，且在2种小角度入流倾角条件下，导管桨的尾流压力环都表现出不均衡状态，可能是斜向流与水平壁面共同作用导致的结果。在相同推进系数J=0.4下，螺旋桨产生的涡环比导管桨的要大一些，与导管桨相比，螺旋桨桨毂区域有明显的低压线，且伴有明显的桨毂涡的特征。

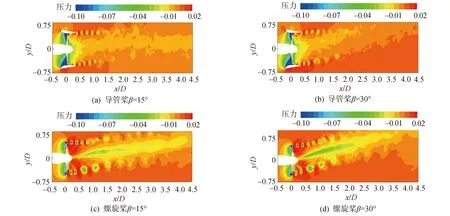
图3 小斜流角度(15°, 30°)导管桨螺旋桨相平均压力对比无量纲化)Fig.3 Comparison of average pressure of ducted propeller and propeller phase with J=0.4 and small oblique flow angle (15°, 30°)，the pressure is normalized by

图4显示了导管桨/螺旋桨不同倾斜角度下相位平均的涡量场变化，导管桨/螺旋桨周围的尾流涡结构是了解导管桨/螺旋桨受力过程的重要依据，导管桨和螺旋桨的涡量场受倾角的影响在图中清晰可见，在特定的进速系数条件下，随着倾斜角度的增加，导管桨中导管产生的尾涡干扰了叶片尾涡的发展，导管桨叶梢泄涡流场与桨毂涡流场发生相互掺混、相互影响，尾涡系统出现失稳或相互作用现象，使得流场涡结构更加复杂，致使导管桨受力发生变化。而螺旋桨由于不存在导管，叶梢涡与桨毂涡的相互作用更加剧烈，流场涡结构比导管桨复杂的多，且螺旋桨有明显的桨毂涡。

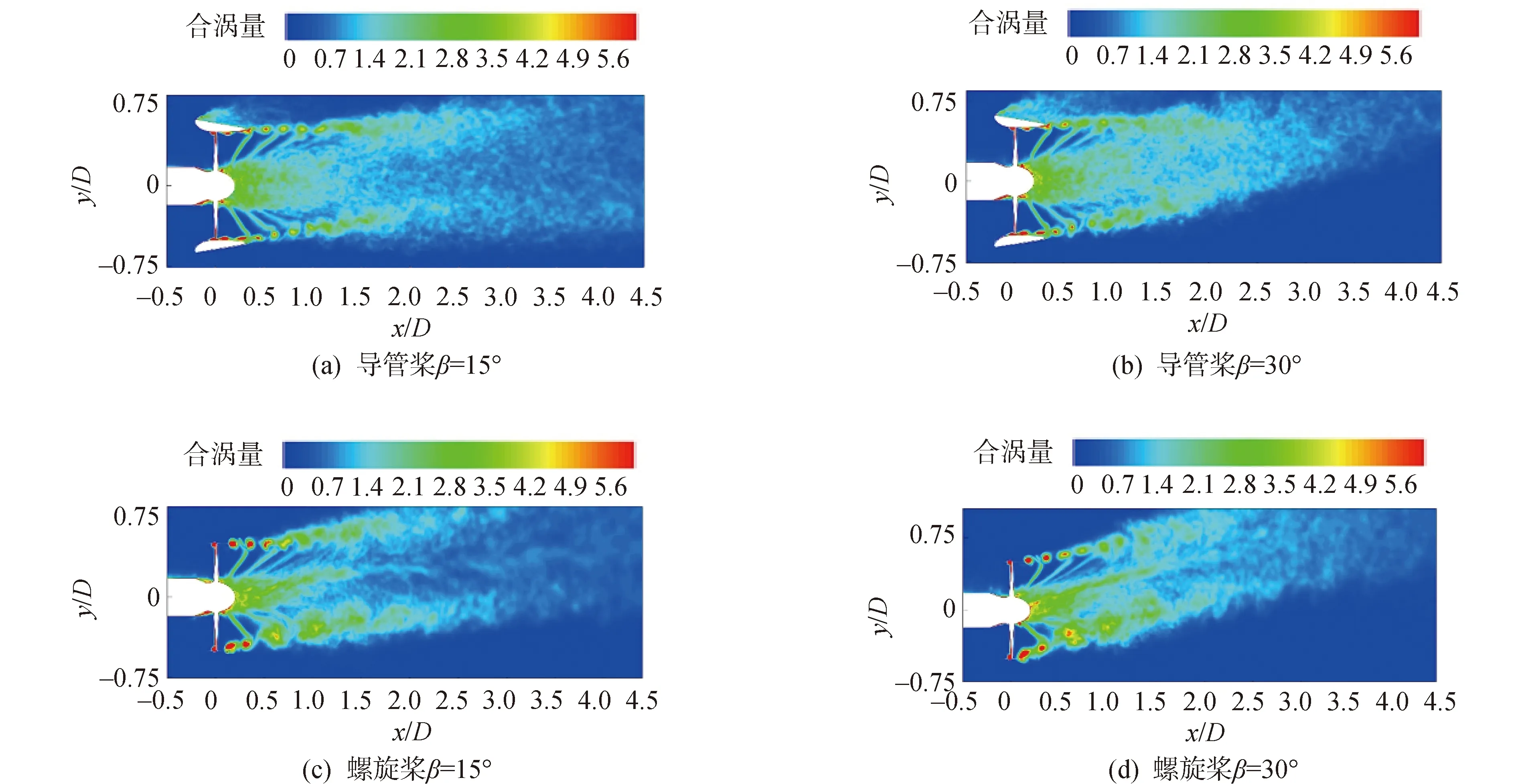
图4 小斜流角度(15°, 30°)导管桨螺旋桨相平均涡量对比(Uref/0.5D无量纲化)Fig.4 Comparison of mean vorticity of ducted propeller and propeller phase with small oblique flow angle (15°, 30°)，the vorticity magnitude is normalized by Uref/0.5D

图5显示了导管桨/螺旋桨在不同倾斜角度尾流场的相位平均动能分布。动能场反应的是流体运动的能量，通过调整入流倾角而使其发展有利于尾涡的相互作用，从而有利于尾涡的失稳和扩散。导管桨和螺旋桨尾流场的能量主要集中在叶梢泄涡和叶梢涡周围形成的环形区域。小倾角斜流导管桨的近壁面尾流动能分布依然表现出不均匀性，与压力场分布一致。此外，在一个特定的进速系数和较小倾角斜流条件下，导管桨和螺旋桨两者的流场动能会集中于涡核并得以保持和延长，并随着倾斜角度的增加，尾涡系统可能会出现失稳或相互作用现象。且在相同进速下，螺旋桨的流场动能都高于导管桨并且有较宽的高动能区域。

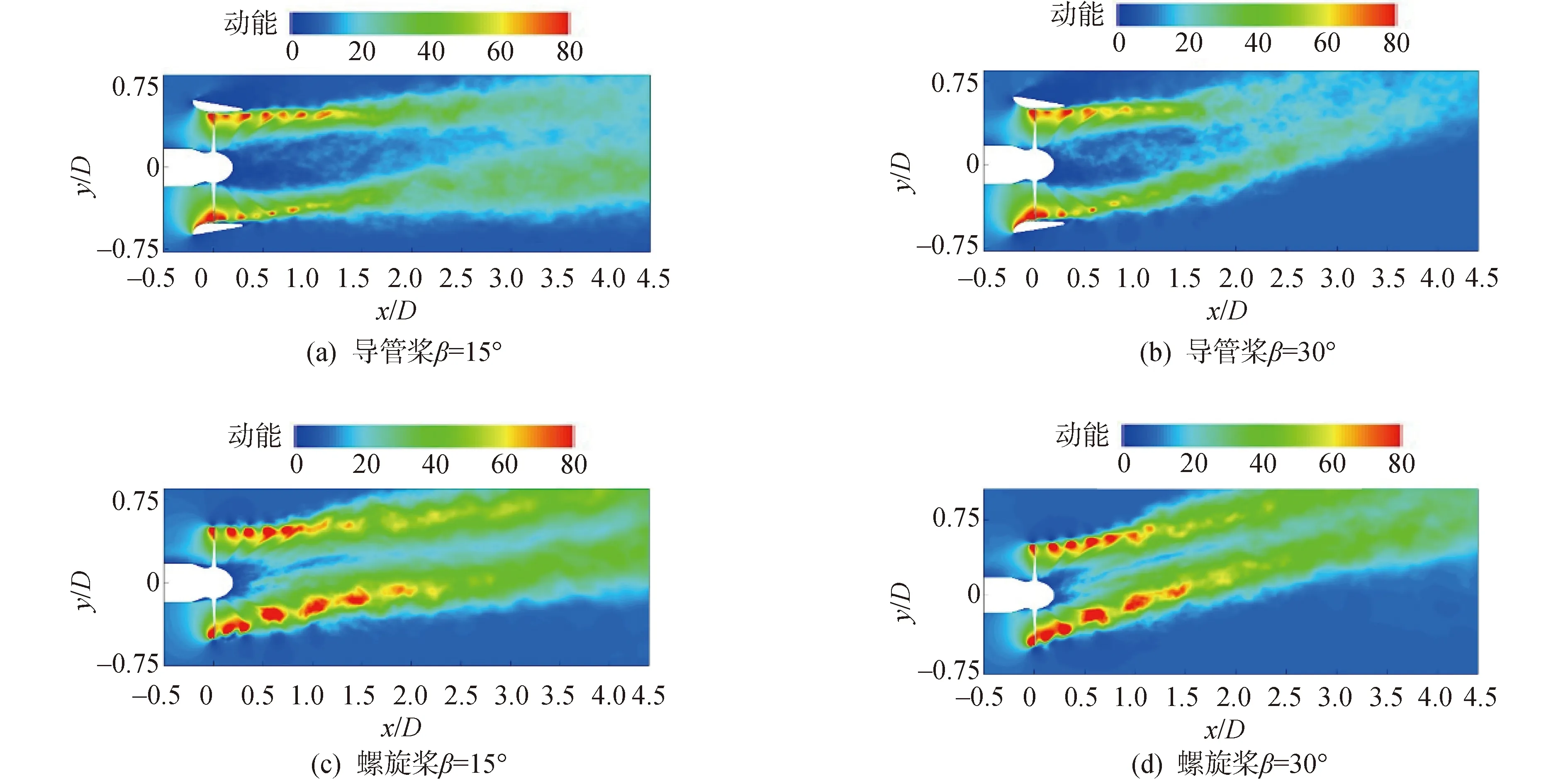
图5 小斜流角度(15°, 30°)导管桨螺旋桨相平均动能对比(Uref无量纲化)Fig.5 Comparison of average kinetic energy of ducted propeller and propeller with small oblique flow angle(15°, 30°)，the kinetic energy is normalized by Uref

图6显示了导管桨/螺旋桨在不同倾斜角度下尾流场的相位平均湍流动能分布。导管桨和螺旋桨的不规则湍流主要由叶梢形成，并随倾斜角度的增加导管桨和螺旋桨的平均湍流动能随之增加。导管桨由于导管的存在，部分叶梢涡的湍流能量转换为导管的推力，剩余能量以叶梢泄涡的形式流出，导管桨尾流湍流能量会减小很多，在相同的进度系数和入流倾角条件下，导管桨尾流湍流能量不如螺旋桨。同时导管桨由于导管尾涡的存在，使得此时湍流动能分布较为复杂。

图6 小斜流角度(15°, 30°)导管桨螺旋桨相平均涡流动能对比(Uref无量纲化)Fig.6 Comparison of average eddy kinetic energy of ducted propeller and propeller phase with small oblique flow angle(15°, 30°). The turbulent kinetic energy is normalized by Uref

关于尾流的瞬时信息，图7显示了导管桨/螺旋桨瞬时涡量场的三维等值面图，在典型进速系数J=0.4条件下，导管桨的叶梢泄涡较为明显，其发展趋势为随尾流逐渐消失于小尺度紊流中，且随着斜流倾角的增加，导管桨的叶梢泄涡更为迅速的与周围流场混合。螺旋桨的尾流涡场会更为复杂，且由于没有导管的存在，使得螺旋桨的叶梢涡的能量高于导管桨，螺旋桨的叶梢涡与周围静止流场会形成较大速度梯度，且迅速与周围流场混合，消散为小尺度紊流。