采用斜装金字塔构型CMGs的敏捷遥感卫星姿态控制*
2022-09-09栾天娇马浩哲
杨 楠 郁 丰 栾天娇 马浩哲
1.南京航空航天大学航天学院,南京 210016 2. 空间光电探测与感知工业和信息化部重点实验室,南京 210016 3. 中国运载火箭技术研究院,北京 100076
0 引言
敏捷遥感卫星通过姿态机动改变遥感相机对地指向来实现对目标的观测[1-2],因此快速姿态机动以及大角度姿态机动能力直接影响观测的灵活性和观测范围的大小,这对其姿态控制系统中执行机构的大力矩输出能力提出了更高的要求。遥感卫星随着航天技术的发展趋于微型化[3],金字塔构型CMG群能够输出大力矩,具有一冗余度且构型相对简单,很适合作为微型遥感卫星执行机构,为其提供强大的姿态机动能力[4]。由于市场上对遥感和对地观测的商业需求逐渐增大,许多国家对敏捷遥感卫星进行研制。大多数遥感卫星以侧摆机动为主要的姿态机动任务,如美国的WorldView系列卫星[5]、国内的“吉林一号”卫星[6]等。前者采用了CMGs作为执行机构,最大可实现±40°侧摆,并在当时能够提供多达10倍以上加速度的姿态控制[5],从而更加精确地瞄准和扫描目标,高效地获取更大范围、更高幅宽的遥感数据。
虽然CMG以其大力矩输出能力、无需消耗燃料的特点被广泛使用,但其固有的奇异问题限制了其应用。一旦陷入奇异,会显著降低遥感卫星获取数据的效率。国内外诸多学者对CMG群奇异问题进行了大量研究,从奇异原理以及构型出发,文献[7]研究了角动量空间和奇异面的可通过性,指出6个及以上CMG构成的系统不存在内部显奇异面,但会抬高成本且不利于卫星的微型化;文献[8]设计了一种构型锥角可动态调整的奇异躲避的路径规划方法,可提高特定方向的机动能力,但是安装结构较为复杂。文献[9]提出了可变构型的控制方法,将安装倾角视为可调变量进行控制,但其在实际应用中的可行性仍需进一步分析。文献[10]分析了CMG与飞轮组成混合执行机构的各类构型,但不利于卫星微型化且陷入奇异时飞轮无法提供较大的力矩。从操纵律出发,奇异鲁棒操纵律[11]、混合操纵律[12]等均引入力矩误差来逃离奇异;文献[13]基于力矩矢量调节的思想克服了一般奇异鲁棒操纵律的“框架锁死”现象。奇异回避操纵律常通过最优初始框架角[14]、全局搜索算法来实现,但同样无法保证回避奇异。因此目前仍然没有一种能够完美解决奇异问题的方法出现。
以往的研究都是基于三维空间中全方位的奇异问题考虑,而非结合实际应用中的需求进行探讨,故本文从敏捷遥感卫星只需要侧摆的姿态机动任务出发,以回避滚动轴方向的奇异问题为主作为研究目标,结合对金字塔构型的内部显奇异面相对原点空隙分布的分析,设计一种面向侧摆机动无显奇异的斜装金字塔构型。为保证提出新型构型的奇异回避能力,采用参考轨迹法对侧摆机动任务预先规划,将角动量轨迹的运动范围约束在滚动轴向附近,设计一种基于实时姿态的侧摆机动控制律,并结合带零运动伪逆操纵律完成侧摆机动。同时,考虑到轨道角速度影响和敏捷遥感卫星的更高需求,对俯仰方向的奇异问题进行分析。最后对某颗低轨卫星的遥感成像任务进行仿真验证。
1 动力学与运动学模型
1.1 坐标系定义
本体坐标系b:原点位于航天器质心,三个坐标轴分别指向卫星的特征轴方向。轨道坐标系o:原点位于航天器质心,x轴指向卫星速度方向,y轴指向轨道平面负法线方向、z轴在轨道平面内指向地心。惯性坐标系i:J2000 坐标系。
1.2 动力学模型
卫星的动力学方程[15]在其本体系下为
(1)

(2)
式中,Is为卫星本体的惯量矩阵,Hcmg为执行机构即CMG群的角动量。
1.3 运动学模型
采用四元数表示卫星姿态,卫星的姿态运动学方程[15]为

(3)

2 构型优化设计
传统金字塔构型CMG群构型如图1所示,其安装倾角β=54.7356°,安装矩阵A、B为
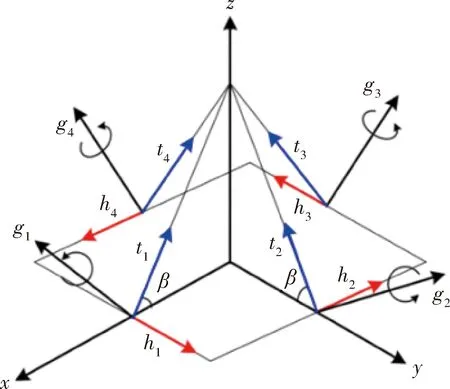
图1 金字塔构型安装方式

(4)
CMG群奇异可分为饱和奇异和内部奇异,其中饱和奇异即CMG群所能提供的最大角动量形成的动量包络,一旦陷入饱和奇异则需要对CMG群进行卸载,内部奇异又分为显奇异和隐奇异,其中隐奇异可以通过添加零运动逃离,不会引入力矩误差,显奇异无法通过零运动逃离,只能通过引入力矩误差的方式逃离。因此内部显奇异是奇异问题的主要矛盾。金字塔构型CMG群内部显奇异面的三视图如图2所示。由图2可知内部显奇异面关于原点中心对称,相对原点存在多处大小类似的空隙。

图2 内部显奇异面三视图
在三维角动量空间中,CMG群角动量轨迹与奇异面的相对位置以及是否遭遇奇异的关系如表1所示。由表1可知,当CMG群的角动量轨迹与奇异面没有交点时,一定不遭遇奇异。故研究CMG群角动量轨迹与内部显奇异面的相对位置关系是本文的重点。理论上卫星在侧摆机动过程中仅产生滚动轴方向的角动量变化,而CMG是基于角动量交换原理的执行机构,根据角动量守恒原理,过程中CMG群的角动量轨迹也仅在滚动轴方向改变。为了防止侧摆过程中角动量轨迹出现偏移,并保证滚动轴方向的可用角动量最大化,降低遭遇饱和奇异的可能,空隙应以以下2个标准进行选取:1)选取的空隙越大越好;2)空隙方向对应的角动量包络值越大越好。基于以上两点考虑,选取空隙方向为[0.6799 0.3633 0.6370]T。

表1 CMG群遭遇奇异条件
综上可知,针对遥感卫星对侧摆能力的要求,若将金字塔构型按照一定的角度斜装,使其内部显奇异面相对原点的空隙方向对准滚动轴方向,则侧摆过程中角动量轨迹一定不会碰到内部显奇异面,从而在理论上能够完全回避内部显奇异。因此需要将CMG群的安装矩阵按照一定角度旋转。在卫星本体系下,滚动轴方向即x轴方向为[1 0 0]T,空隙方向[xyz]=[0.6799 0.3633 0.6370]T,令
(5)
故使得空隙对准滚动轴方向的旋转矩阵为
(6)
由式(4)~(6)可得面向侧摆机动的无显奇异的斜装金字塔构型的安装矩阵。
3 姿态控制律及操纵律设计
3.1 姿态控制律设计
由于内部奇异面相对原点的空隙大小是有限的,一旦CMG群角动量轨迹偏离空隙方向,极有可能碰到内部显奇异面,导致斜装金字塔构型对奇异回避的可靠性降低。而遥感卫星进行大角度侧摆时,若不对其角速度、角加速度进行限制,初始时刻较大的姿态偏差可能会导致CMG群角动量轨迹偏离滚动轴向。因此基于参考轨迹法制定侧摆机动方案,能够有效将角动量轨迹的运动范围限制在机动轴方向,保证它不会与内部显奇异面相交。
基于参考轨迹法的遥感卫星侧摆机动方案设计如下:将卫星的机动过程分段为加速段、滚动段和减速段;将卫星角速度设计为
ω(t)=e(0)ω(t)
(7)

(8)
式中,e(0)为初始时刻本体系相对于目标系的欧拉轴矢量,即滚动轴的方向矢量,ω(t)为角速度幅值,t0为初始机动时刻,a为本体系相对于目标系的角加速度,表达式为
(9)
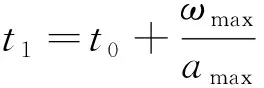
本体系相对于目标系的角速度始终沿滚动轴向,则本体系相对于目标系的欧拉角和姿态四元数为

(10)
q(t)=[esin(θ(t)/2) cos(θ(t)/2)]T
(11)
由式(7)~(11)完成轨道系下卫星侧摆机动方案的设计,结合该方案,采用PD控制律,根据时变期望姿态来调节误差并进行稳定性控制。由此可得基于实时姿态的侧摆机动控制律,设计如下:

(12)
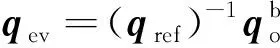
3.2 CMG群操纵律
采用传统的正装金字塔构型时,常采用广义奇异鲁棒操纵律,在系统陷入奇异时引入相对较大的力矩误差逃离奇异,但这种操纵律的缺点是在系统非奇异时,也会存在一定的力矩误差。对于本文提出的侧摆条件下无显奇异的斜装金字塔构型,结合上一节设计的侧摆机动方案,在机动过程中一定不会碰到显奇异,但不能排除遭遇隐奇异的可能,因此采用带零运动的伪逆操纵律。计算公式如下。
(13)

(14)
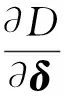
4 仿真验证
选取一条低轨圆轨道作为遥感卫星的工作轨道,轨道周期5678.98s,高度500km,偏心率0,轨道倾角45°。针对卫星滚动通道60°方向某目标区域进行成像的任务,设置绕滚动轴机动60°的姿态控制要求。分为2组进行闭环仿真,仿真参数[16]如表2所示。第1组执行机构采用正装金字塔构型的CMGs,使用广义奇异鲁棒操纵律;第2组执行机构采用斜装金字塔构型的CMGs,使用带零运动的伪逆操纵律。两组均按照基于参考轨迹法的侧摆机动方案进行控制。仿真结果如图3~7所示。

表2 仿真参数
图3为两组仿真轨道系下的姿态角速度曲线。仿真结果表明两种构型均在30s左右将卫星控制到期望姿态,顺利完成了60°的滚动轴姿态机动任务。采用正装金字塔构型时,卫星姿态角速度在逃离奇异过程中会产生抖动,采用斜装金字塔构型时与参考轨迹基本吻合。
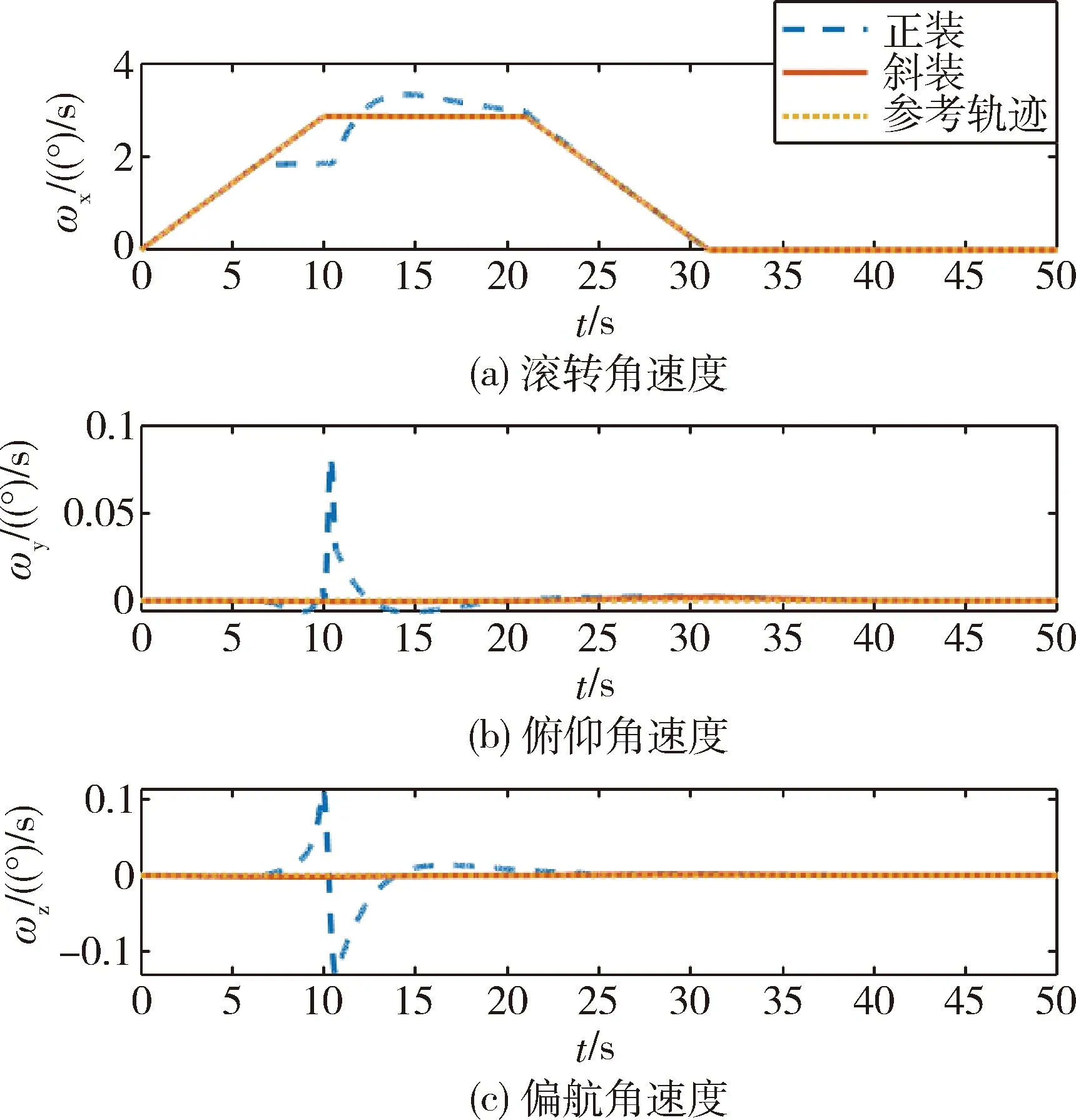
图3 轨道系下卫星角速度仿真曲线图
图4为两组仿真的奇异度量曲线,仿真结果表明采用正装金字塔构型时,系统在6.5s陷入内部显奇异面,10.2s完成逃离;采用斜装金字塔构型时,整个仿真过程中奇异度量值始终大于0,成功避开了内部显奇异面。图5和6分别为两组仿真的框架角位置曲线和框架角速度曲线,仿真结果表明采用正装金字塔构型时系统陷入内部显奇异,驱动框架以其最大角速度工作逃离;采用斜装金字塔构型时系统未遭遇奇异,框架角以及框架角速度均在相对较小的范围内变化。
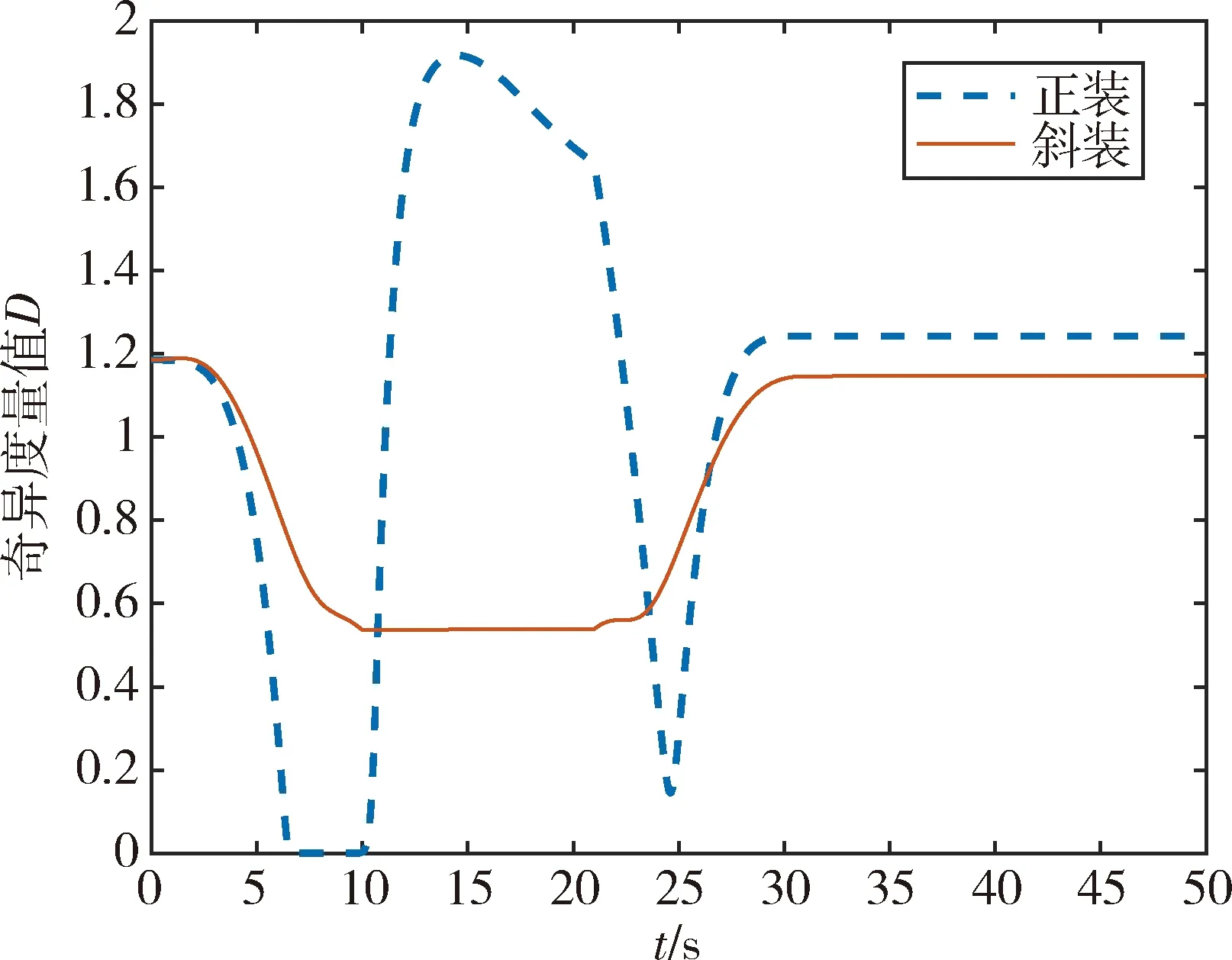
图4 奇异度量值仿真曲线图
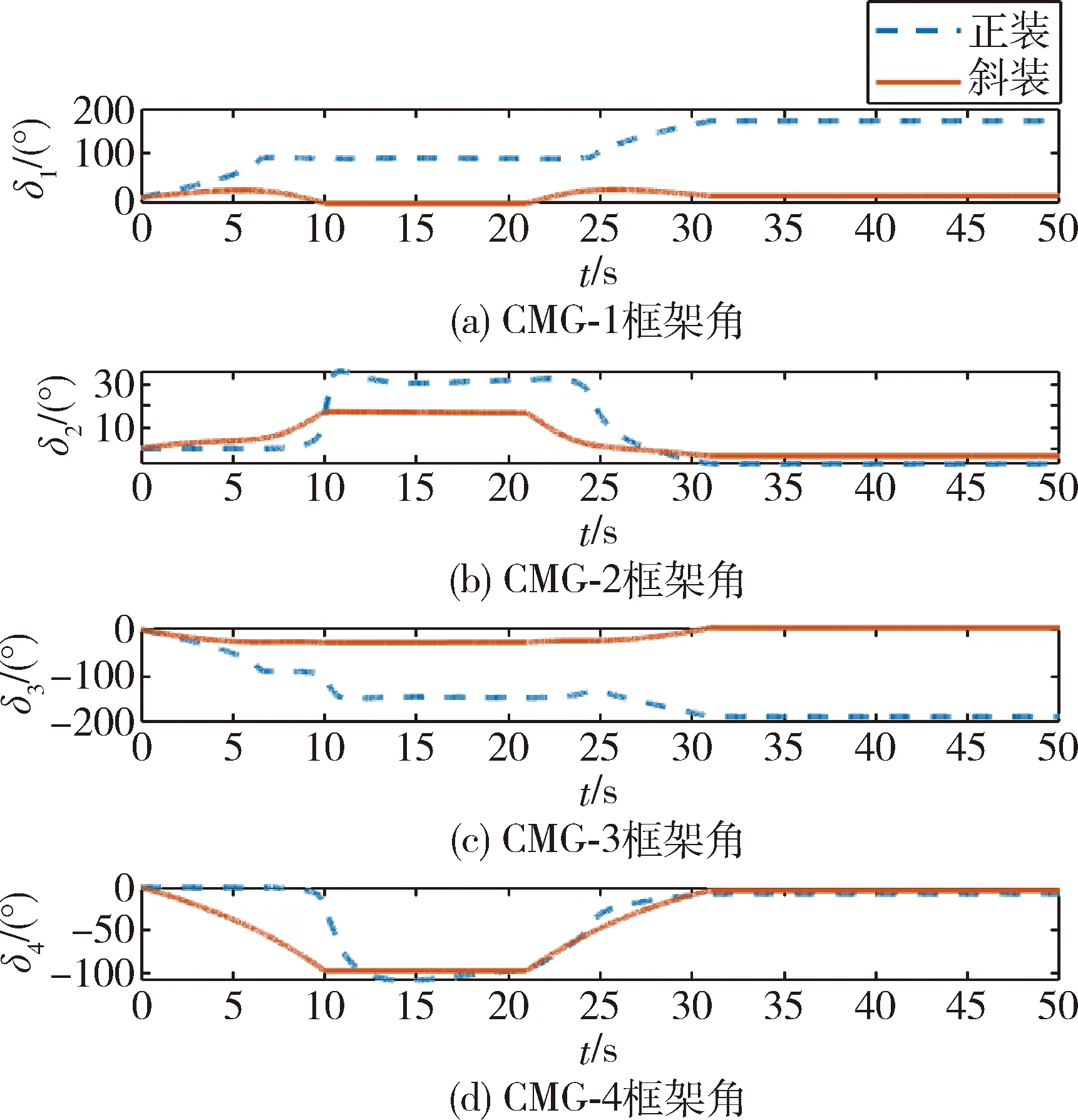
图5 框架角仿真曲线图

图6 框架角速度仿真曲线图
图7为两组仿真的侧摆角误差曲线,仿真结果表明采用正装金字塔构型时,由于系统陷入内部显奇异,在逃离过程中会引入力矩误差最大为59.71N·m,从而产生侧摆角误差最大为2.94°;采用斜装金字塔构型时,由于系统成功回避了内部显奇异,输出力矩能够高精度地跟踪指令力矩,此时几乎不产生侧摆角误差。

图7 侧摆角误差仿真曲线图
由于卫星俯仰方向也会存在干扰力矩,因此需要对该轴向的奇异问题进行分析。侧摆机动过程中俯仰轴方向产生的最大角动量为0.0162N·m,而斜装金字塔构型的角动量包络在俯仰轴上约为149N·m,内部显奇异面在俯仰轴上的最小值约为64N·m,均远大于0.0162N·m。因此斜装构型能够保证在侧摆机动过程中俯仰轴方向不会遭遇内部显奇异和饱和奇异。
另一方面,由于敏捷成像卫星对卫星姿态控制的要求日益提高,针对俯仰方向奇异问题的研究也具有现实意义。例如法国的Pleiades卫星,除了传统侧摆成像模式,也可以通过俯仰轴机动推扫,完成立体成像等新型成像模式。因此同样可以从优化构型出发,改变安装矩阵,使滚动轴和俯仰轴均指向内部显奇异面的空隙。由图8可知,在本文的旋转基础上沿滚动轴二次旋转,能够得到一种兼顾侧摆和推扫均无显奇异的构型方案。
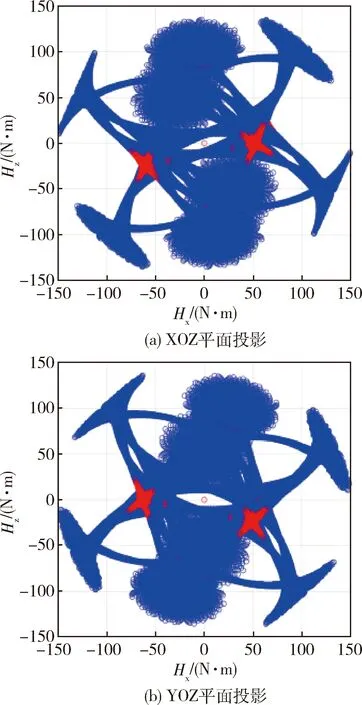
图8 斜装金字塔构型CMG群内部显奇异面投影
5 结论
面向敏捷遥感卫星侧摆机动,提出了无显奇异斜装金字塔构型,结合带零运动的伪逆操纵律,按基于参考轨迹法设计的侧摆机动方案进行姿态控制。仿真结果表明该构型方案能够成功回避内部显奇异,显著降低了以往因逃离显奇异引入的侧摆角误差,将奇异对卫星姿态的影响降到最低,满足了敏捷遥感卫星的任务需求。
