空间超长波天线绳系系统动力学建模与分析

高怀旭 张晓敏 徐 瑞

北京理工大学宇航学院，北京 100081

0 引 言

超长波(Extremely low frequency，ELF)通信又称超低频通信，指信号频率在30 Hz ～ 300 Hz的电磁波通信模式。超长波具有抗干扰能力强，衰减率低的优点，非常适合超长距离通信，在民用和军用领域都有着广泛的应用。然而，超长波通信的理论优势应用在实际中，仍然面临一些困难。根据波长与频率的反比关系，超低频的信号需要匹配极大尺寸的天线。传统的超长波天线安装在地面上，不方便机动和隐蔽，且容易受到地面上山川河流或者建筑物的阻碍影响。空间超长波天线则另辟蹊径，借助日趋成熟的卫星技术进入近地空间。天线在地外环境中展开不受任何空间上的约束，受地面干扰极小，而且天线还可随着卫星的轨道机动而机动，极大增加了其应用范围。截至目前，关于空间超长波天线系统的理论研究和空间实验很少。不过，该系统的理论模型与绳系卫星有很高的相似性。

绳系卫星系统(Tethered satellite system，TSS)主要是指由两颗卫星(一般根据功能区分为主星、子星)和一根系绳组成的二体航天器。自20世纪提出以来，因其在清除空间碎片[1]、轨道转移[2]、人工重力[3]、系绳编队[4]等方面具有重要的应用，受到研究人员的的持续关注[5]。在目前已经开展的绳系卫星实验中，系绳的材料以非导电材料为主，这种材料柔性大，易弯折；普通的金属材料系绳虽然能导电，但重量大，不易收纳和展开。这两类材料都不具备充当空间超长天线材料的可能。碳纳米管作为一种新型高分子材料，密度低，导电性能好，延展性强。千米级的碳纳米管绳，可以被收纳到容积为2L的盒子里，这就为空间超长天线系统的构建提供了材料上的支持。

搭载着超长天线的卫星进入轨道后，其最终目的是将千米级的天线展开，并保持对地稳定，如此才能完成信号的传输。因此对于空间天线展开的动力学建模尤为重要。参考绳系卫星的研究，对于展开过程的动力学建模主要有以下几种方法[6]：1)运用Lagrange方程建立的杆模型(哑铃模型)[7]；2)运用牛顿第二定律的珠链式模型；3)运用绝对坐标节点法的有限元模型。

赵国伟等[8]基于哑铃模型设计了绳系卫星轨道机动中的连续推理控制方法。William[9]则在刚性杆的基础上设计了绳系卫星对于目标捕获的控制方法。朱兵等[10]针对哑铃模型提出了一种新的离散控制绳系无超调释放的方法。杨育伟[11]等研究了系统参数对电动力绳系动力学的影响。胡仄虹等[12]基于珠链式模型建立了空间绳系机器人的动力学方程组，并给出了一种高效时域求解算法。Mankala等[13]采用有限元法建立了系绳释放和回收两个过程的动力学模型，并进行了离散化求解。Ellis等[14]基于有限元模型完成了电动力系绳建模工作。

珠链式模型和有限元模型为了提高精度必须增加相当数量的质点，但这会增加计算量和求解的复杂性。而在以往采用Lagrange法建立的杆模型中，经常忽略系绳的质量、弹性以及在系绳释放过程中整个系统质心的变化。刚性杆模型不能体现出系绳在释放过程中的弹性势能的变化以及其中的阻尼损耗。对于释放过程的稳定性，大部分的研究都着重于控制方法的设计，忽视了释放条件对于系统的影响。

针对上述研究中的不足，本文依托北理工2号卫星(BP-2)的工程项目，采用Lagrange法建立了有弹性、有阻尼、变质量的动力学方程来描述超长波天线绳系系统的释放过程，并根据释放条件对于系统的影响情况，设计了最优释放初值。

1 绳系系统建模

1.1 系统组成

超长波天线绳系系统由两颗卫星和一根千米级的碳纳米管绳组成，两颗卫星根据功能区分为主星、子星。卫星发射前，主星和子星通过爆炸螺栓紧固连接在一起，碳纳米管绳盘绕在收纳盒中。

北理工2号卫星计划运行在轨道高度370km、轨道倾角97°的太阳同步轨道上。发射入轨后，卫星在空间飞行试验中解锁爆炸螺栓，由弹簧将主星和子星推离，初始相对速度约1m/s。系绳为纯碳纳米管材料，总长度1080m，直径约1mm，线密度为0.8g/m。

1.2 坐标系定义

为描述绳系系统在空间的运动状态，本节将介绍下列3组坐标系：

1)地心惯性坐标系：以地心O1为原点，X1轴指向春分点，Z1轴与地球自转轴方向一致，Y1轴由右手法则确定；

2)轨道坐标系：以绳系系统的质心O为原点，Z2轴指向地心，X2轴指向系统飞行的方向，Y2轴由右手法则确定；

3)本体坐标系：以绳系系统的质心O为原点，由主星指向子星的方向为Z轴。本体坐标系可由轨道坐标系经过2次旋转得到，2次旋转的角度记为θ和φ，称为绳系系统的面内角和面外角。释放绳长l、面内角θ和面外角φ，描述了空间绳系系统的基础运动状态。

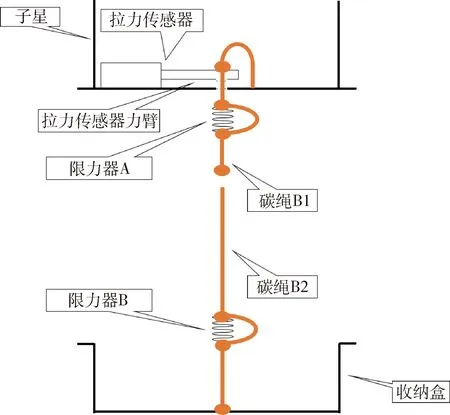
图1 北理工2号绳系卫星的连接方式

图2(a) 惯性系与轨道系

图2(b) 轨道系与本体系

1.3 释放阶段动力学方程建立

绳系系统释放阶段的动力学服从理想约束条件，因此采用分析力学的方法推导动力学方程。这种方法需要先计算系统的动能和势能。为使建立的模型可计算可分析，现做出如下几个假设：

1)考虑到绳系系统从开始释放到相对稳定的时间远少于离轨时间，因此认为在释放期间，整个系统运行在轨道高度不变的圆轨道上，忽略其他因素对于轨道的摄动影响；释放过程中关闭电子收发装置，无洛伦兹力的产生；

2)主星和子星在建模中视为质点，不考虑其姿态对于系绳的影响；

3)系绳在释放过程中始终呈直线，不考虑系绳的柔性。由于在实际的绳系卫星实验中，系绳的长度常常达到千米级甚至十几千米，因此在计算中需考虑系绳的质量和弹性，同时也考虑系绳释放过程中对于主星质量的影响、对于系统质心的影响。

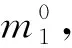
各部分质量表达式为

(1)

考虑系绳质量变化和系统质心变化的等效质量m*和m#表达式为

(2)

下面直接给出系统动能、重力势能和弹性势能的表达式[15]

(3)

取拉格朗日函数L=T-V1-V2，建立含有耗散函数的第二类拉格朗日方程

(4)

求解拉格朗日方程中需用到的等效质量对时间和绳长的导数如下

(5)

三个广义坐标分别为q1=θ,q2=φ,q3=l。在自由释放过程中，无主动力的控制和外界摄动力的作用，广义力Qqi=0。

为提高方程解算精度，引入无量纲化处理

(6)

定义如下质量系数

(7)

最终得到的无量纲化的动力学方程为

(8)

2 绳系释放过程仿真

本节将对第1节中所建立的绳系释放动力学模型进行仿真计算，仿真环境为Windows 10，Matlab和ode45 Runge-Kutta积分器。仿真中所用的物理参数来源于北理工2号绳系卫星。根据北理工2号卫星的预设工况，本小节设置释放初始面内角θ0=5°，初始面外角φ0=1°，其余参数设置如表1所示。

表1 北理工2号绳系卫星参数

图3和4展示了绳系系统的三个广义坐标随时间的变化情况。从中可以分析出：系绳释放长度在首次达到标称长度后，迅速下降至一个波谷，然后再次上升至标称长度，如此反复几次。最终在系绳阻尼的作用下趋于稳定，整个过程持续时间约为0.7个轨道周期。面内角在释放过程中会随着时间进行一定幅度的振荡变化，且并不收敛。面外角在整个释放过程中也随时间进行周期性振荡，但其振荡幅度始终很小(-0.6°～0.6°)。因此，可将三维空间内的绳系卫星释放过程，简化至二维平面内。

图3 无量纲绳长随时间变化图

结合3个广义坐标的变化情况，可以得出绳系系统释放时的运动规律。在释放的初始阶段，子星相对主星的运动可以看成是遵循C-W方程的相对运动。当系绳释放至标称长度时，其产生的张力促使子星迅速向主星所在方向回摆，主星和子星之间的距离缩短，系绳变为松弛状态，整个系统也进入新的运动状态。当两颗立方星之间的距离再次达到标称长度时，系绳再次张紧，子星再次回摆，如此循环若干次最终由于系绳上的弹性势能不断被其阻尼耗散，系绳释放长度趋于稳定，两颗立方星之间的距离也不再变化。但由于面内角无法收敛，在无其它外力的扰动和控制下，子星将相对于主星做周期性的圆弧形摆动，摆动幅度为-15°～15°。

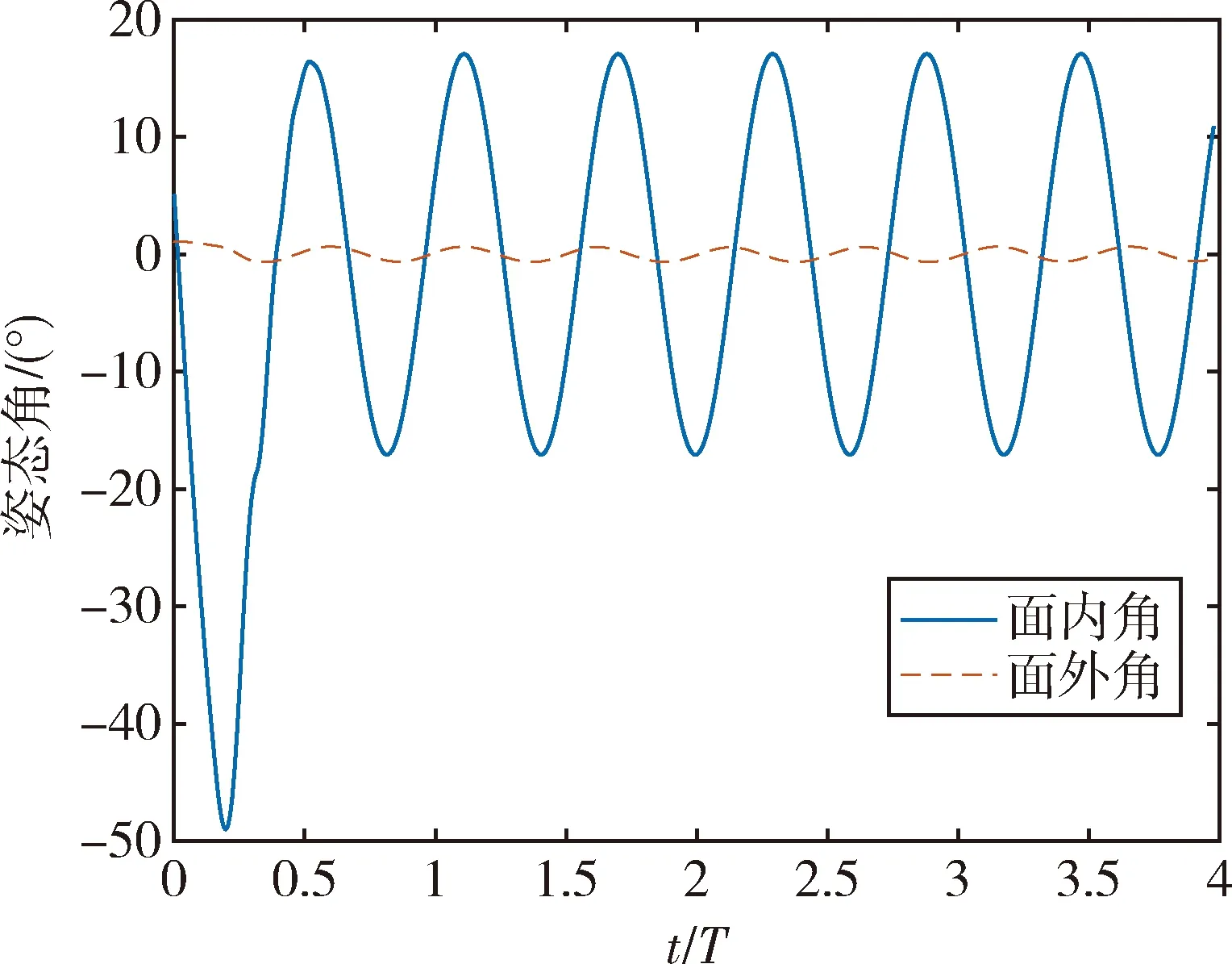
图4 面内角和面外角随时间变化图

3 释放动力学特性分析

3.1 绳系释放初值对于系统运动的影响

在绳系系统开始释放时，子星的相对运动方向(即绳系系统面内角初值)和速度大小，会影响到整个系统的运动状态和最终达到稳态的时间。本小节对此进行仿真计算，选取一组初始面内角θ0=[5°,10°,20°,40°]和速度v0=[0.5,1,2,2.5]m/s。

图5展示了在初始释放速度为1 m/s的情况下，不同的面内角初值对系统运动状态的影响。随着面内角初值的增大，释放完毕后系统面内角的振荡幅随之减小。当面内角初值增加至40°时，最终的振荡幅值大幅度降低(-5°～5°)。由此得出，面内角初值即系绳释放的初始方向，对系统的稳定性有很大影响。另一方面，面外角的振荡幅度同样会随着面内角初值的增加而增加，但相比于面内角仍然很小。

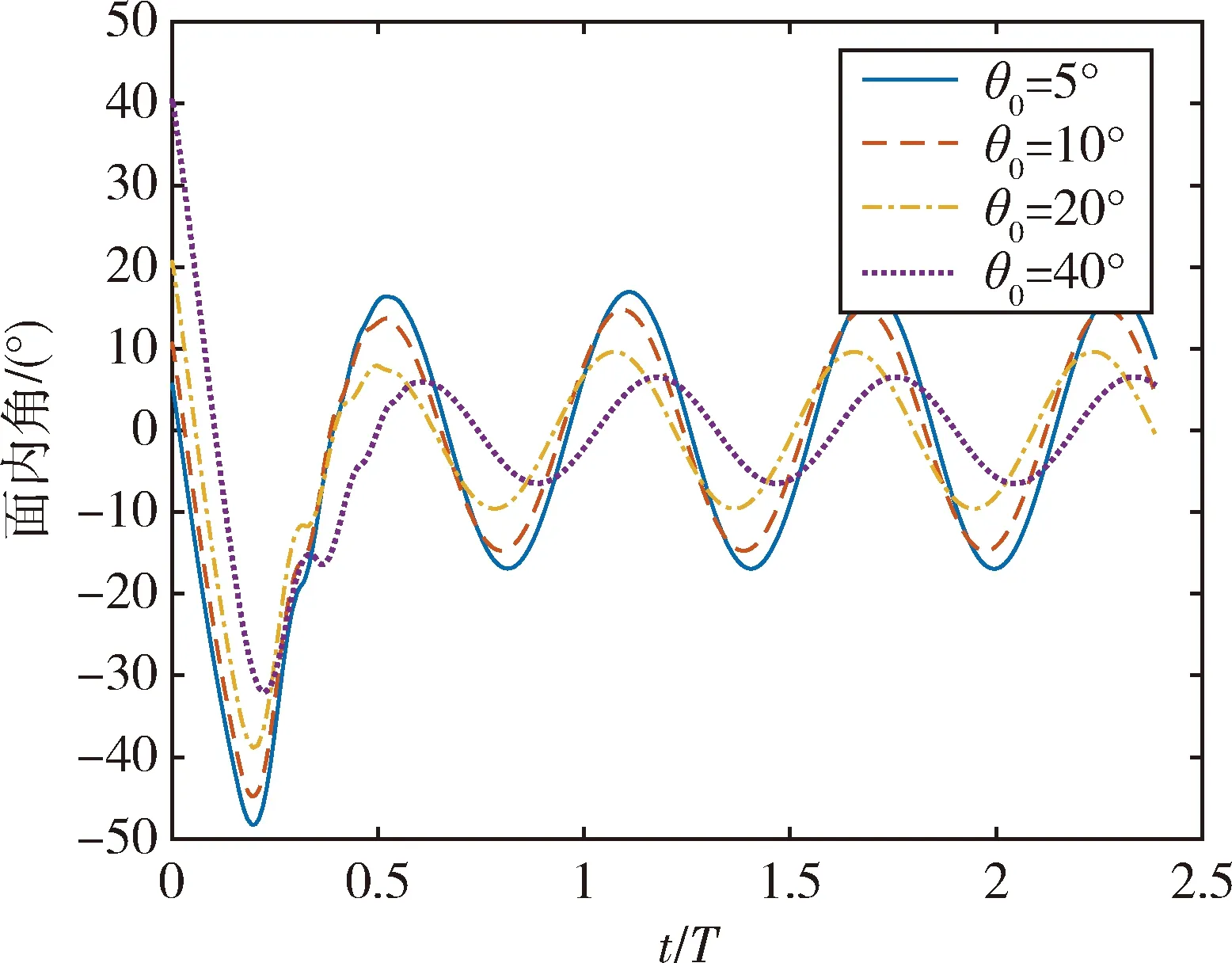
图5 不同面内角初值下的面内角变化曲线

图6和图7展示了在初始面内角为5°的情况下，释放初速度对系统运动状态的影响。当初速度为2.5m/s时，绳系系统的运动状态相比于1 m/s时，都产生了较大的变化。面内角在-50°～50°的范围内大幅度振荡；预设工况下振荡幅度很小的面外角振幅也达到了-8°～8°，系统有随时翻转、失稳的可能，抗干扰能力很弱。由此可见，应将2.5m/s设为释放初速度的安全上限。

图6 不同释放初速度下的面内角变化曲线

图7 不同释放初速度下的面外角变化曲线

3.2 系绳最优释放初值分析

已有文献表明[17]当系绳摆角接近50°，系绳会松弛。若绳的摆幅过大，如90°，此时，主星和子星之间的重力梯度力会消失，在外界的轻微扰动下很容易导致整个绳系卫星系统发生翻滚，使其空间任务失败。

根据3.1小节中的研究，已经初步得到面内角和面外角的摆幅变化规律。本小节将会在一定区间内采用遍历法，寻找北理工2号绳系卫星的最优释放初值。

给定面内角初值区间[1°,40°]、释放初速度区间[0.5,1.5]m/s。将绳系系统释放稳定后面内角和面外角的摆动幅度(极值)分别记为θs和φs，通过遍历法寻找两者之和的最小值。

遍历计算的结果如图11所示，经比较、检验，当θ0=35°、v0=1.15m/s时，绳系系统稳定后的面内角、面外角振荡幅度最小，振荡幅值之和在3°以下，相比于预设工况释放条件下的运动情况， 最优释放条件使整个系统的摆幅降低了80%，大大提高了稳定性，也为后续的主动力控制减轻了负担。

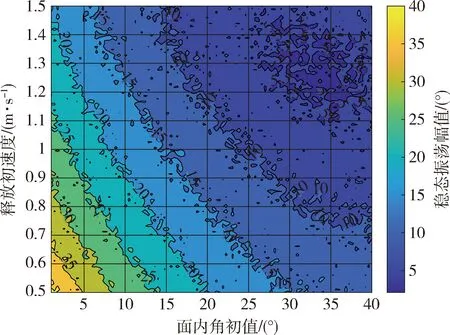
图8 释放初值与振荡幅值的等值区域图

4 结论

以空间超长波天线绳系系统为研究对象，依托北理工2号卫星的实际工程参数，使用Lagrange方法，充分考虑系绳的质量、弹性和阻尼耗散，建立了变质量、变质心的绳系系统释放过程的动力学模型。分析了绳系释放从开始到相对稳定的全运动过程，探究了系绳释放初速度和面内角初值对于系统运动和稳定性的影响，指出在一定范围内随着面内角初值的增加，系统最终的振荡幅度会减小。计算得到系统的最优释放条件(θ0=35°、v0=1.15m/s)，为北理工2号卫星绳系系统的工程方案设计提供了理论依据。