基于T型传递函数的二进制樽海鞘算法求解0-1背包问题

王原 李晓苗

（河北地质大学信息工程学院 河北省石家庄市 050031）

1 引言

背包问题(Knapsack problem,KP)是计算机科学中的一个重要的NP 完全问题，同时也是一个经典的组合优化问题，在投资决策，能量最小化和资源分配等方面有着重要的应用背景。0-1 背包问题（0-1 Knapsack Problem,0-1KP）是最基本的背包问题。其一般描述为：从n 个具有价值系数与重量系数的物品（或项）中，选择若干个装入一个具有载重限制的背包，如何选择才能使装入物品的重量系数之和在不超过背包载重的前提下价值系数之和达到最大？

目前，对于0-1KP 的求解方法，主要分为两类，确定性算法和非确定性算法。确定性算法如分支定界法、动态规划法等，虽然可以求得精确解，但其时间复杂度都是伪多项式时间，随着0-1KP 规模不断增大，其求解速率也不断急剧下降，因此，确定性算法并不适合求解大规模的实例。非确定型算法如演化算法，则避免了确定性算法的局限性，不需计算目标函数的导数也不需要目标函数具有连续性，已成为求解0-1KP 的最重要的方法。

樽海鞘算法(Salp Swarm Algorithm，SSA)是由Mirjalili等人提出的众多元启发式算法领域中的算法之一。该算法的灵感来自于樽海鞘群在海洋中群体觅食的行为并用于求解连续优化问题。在海洋中，樽海鞘群成一条樽海鞘链来进行整个群落的移动与觅食。随着种群的不断迭代，种群个体逐渐接近所搜寻的食物位置。随着SSA 的提出，近年来出现了许多将其应用于求解各类问题的研究。例如，Rizk-Allah 等人基于反三角变化提出了一种新颖的二进制樽海鞘算法；Faris 等人提出了一种带有交叉算子的二进制樽海鞘算法用于求解特征选择问题等。

本文在传统樽海鞘算法的基础上，借助T 型传递函数，对算法进行离散化，提出一种求解0-1KP 的二进制樽海鞘算法。在樽海鞘算法的框架下，使其能够对离散域上的0-1KP进行求解。并通过对0-1KP 实例的仿真计算，与6 个演化算法进行比较，验证了所提出算法求解0-1KP 的有效性及鲁棒性。

本文的大致结构如下：

首先，给出了0-1KP 的定义与数学模型，并介绍了传统的樽海鞘优化算法；然后，对所提出的二进制樽海鞘算法进行了介绍，并给出了利用BSSA 求解0-1KP 的具体方法；最后，与其他求解0-1KP 的算法进行比较并分析结果，同时，对本文进行了总结。

2 相关背景

2.1 0-1KP的定义与模型

0-1KP 是一个经典的组合优化问题，对其可以进行如下的定义：

给定一个具有固定载重C 的背包和n 个物品的集合N={1,2,…,n}，每个物品i 具有其两个正值属性：载重w(>0)和利润p(>0)(i=1,2,…,n)。对于每个物品，有两种选择情况：装进背包则x=1；不装进背包则x=0。

其具体数学模型如下：

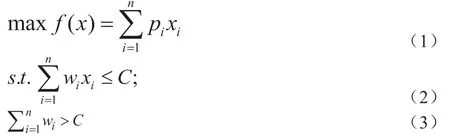
其中：x∊{0,1}，i=1,2,…,n，n 为物品数量；p为物体i的利润；C 为背包载重，w为物体i 的重量。

2.2 樽海鞘算法

SSA 的主要思想来自于深海中一种被称为樽海鞘的海洋生物，这种生物是一类小型远海胶质脊索动物。其在海洋中的移动与觅食行为，常常是以一种链式的集群方式进行的。在SSA 中，种群个体被分为两种角色，一种被称为领导者，负责领导整个种群个体向着食物位置进行移动，另一种被称为追随者，在种群中跟随领导者的引导进行行动。

SSA 的演化过程可以描述为：首先确定食物来源，在确定食物来源后，由领导者根据食物来源对自己的位置进行更新调整，同时追随者根据领导者的位置对自己的位置进行更新调整。以致在一次次迭代更新的过程中，整个种群愈发接近食物的位置。

基于以上描述，给出所涉及到的数学公式：

（1）对于领导者个体，在SSA 中一般选择种群第一个个体作为领导者，其位置的更新公式如下：

其中，x代表领导者个体位置向量的分量，F代表代表食物在第j 维的位置向量的分量，c是一个变量，其值的大小随着算法的迭代过程逐渐减小，具体计算公式如公式5 所示，c,c是两个取值在[0,1]中的随机数。ub和lb是第i 维分量的上下限。

对于参数c的计算公式如下：

其中，l 为算法当前迭代次数，L 为最大迭代次数。

（2）另外，对于种群中追随者的位置，更新公式为：

其中，i>1，x代表第i 个追随者个体在第j 维的位置向量的分量。

由以上计算公式以及过程描述，可得出SSA 的算法伪代码如下：

3 二进制樽海鞘算法

3.1 T型传递函数

由于，樽海鞘算法是被设计来求解连续域上的优化问题，0-1KP 是离散的组合优化问题，为了使SSA 能够用于求解0-1KP，所以将传递函数引入到SSA 进行离散化。目前，已有的演化算法都是基于实数运算求解连续域上的问题，因此不能直接求解离散优化问题。为此相关研究人员提出一种映射的方法，通过传递函数将个体的实向量编码映射为一个0-1向量编码，以适合直接用于求解二元优化问题。目前，主流的传递函数共有S 型和V 型两种。具体形式如表1所示。

表1：S 型传递函数和V 型传递函数

随着近年来的研究不断加深，张等人提出一种新型的传递函数，称为T 函数，具体形式如公式（7）所示：

在文献中张等人详细的讨论了T 型传递函数相较于其他传递函数的优势，如计算量小，时间复杂度低，计算复杂度低等。并进行了仿真实验进行了测试比较用来验证。

因此，本文采用新型的T 型传递函数对传统SSA 进行离散化，具体过程为：

设Y=[Y,Y,…,Y]表示BSSA 中第i 个个体，其中，Y∈[–A,A]，j 是问题维数，BSSA 利用T 函数将Y转化为一个n维0-1向量，X=[x,x,..x]，X为一个可行解或潜在解，接着根据传统SSA 的流程（如算法1 所示）继续进行BSSA的演化过程。

3.2 利用二进制樽海鞘算法求解0-1KP

3.2.1 个体编码及不可行解的修复优化

在BSSA 中，个体编码为Y=[Y,Y,…,Y]∈[–A,A]，利用传递函数转换后为X=[x,x,..x]∈[0,1],x=1，表示物品装入背包，反之，则不装入，然后利用4.2 所采用的修复优化将其转换为可行解。综上，BSSA 的个体编码为一个经过传递函数转换后的n 维0-1 向量。

由于0-1KP 是约束优化问题，利用BSSA 求解0-1KP 时会不可避免地产生不可行解，这会导致不能直接使用目标函数值评判个体适应度的好坏。因此我们要找到合适的方法处理不可行解。目前处理不可行解的方法一般有：罚函数法、修复法和修复与优化法。本文采用了文献提出的贪心修复优化方法（GROA）来处理不可行解。

3.2.2 求解过程及算法流程图

利用BSSA 求解0-1KP 的具体步骤如下：将物品集中的n 个物品的序号按照价值密度比（p/w）由大到小存储，随机初始化种群并利用传递函数将实数向量转化为0-1 向量，再利用GROA 对种群中所有个体进行修复优化并排序。然后重复如下过程直至满足终止条件：用公式（5）更新参数c，随机产生c和c，用公式（4）更新领导者位置，用公式（6）更新追随者位置，利用传递函数将个体转化为0-1 向量，进行修复优化并排序。最后，输出最优解F。

BSSA 算法流程图如图1所示。

图1：BSSA 算法流程图

4 仿真计算与结果比较

4.1 仿真环境与实例

本文所有仿真计算在处理器为AMD Ryzen 7 4800H with Radeon Graphics 2.90 GHz 机带RAM 为16.0 GB (15.9 GB 可用)的Leigon R7000P2020H 的设备上进行。操作系统为微软的Windows10。编程语言为C 语言。利用Visual C++ 6.0进行编译。所采用0-1KP 实例的维数为1000，2000 的0-1KP实例，依据相关程度分为：

（1）不相关实例；

（2）弱相关实例；

（3）强 相关实例；

（4）反向强相关实例（即Ukp，Wkp，Skp，Ikp）共16 个实例。

4.2 仿真结果比较

为了验证SSA-T 的有效性，在独立运行20 次迭代与维数相同次数的情况下进行求解，与GA(遗传算法)，BPSO（二进制粒子群算法），HBDE（差分演化算法），BinABC（人工蜂群算法），BWOA（鲸鱼优化算法），GTOA（基于群论的优化算法）6 个演化算法进行比较，具体结果如表2，表3所示。其中Best 列代表最优值，Avg 列代表平均值，Std 列代表标准差。

表2：BSSA,GA,BPSO,HBDE 实验结果比较

表3：BSSA,BinABC,BWOA,GTOA 实验结果比较

由上两表可知，BSSA 在求解16 个实例的结果中，对于最优值而言有15 个实例取得了OPT 值，在一共7 个算法中，与BWOA 并列第一；对于均值而言，BSSA 有13 个实例的均值取得了最优，位列7个算法中的第一，对于Std而言，BSSA 求解的15 个实例的Std 均处于较小的数值，证明其求解稳定性明显优于其余的6 个算法。

综上，BSSA 对于求解0-1KP 具有一定的算法优越性与鲁棒性，与其他6 个算法相比，不仅在求得最优值方面具有优良的性能，与此同时，还能够保证求解的稳定性，因此，对于求解0-1KP 而言，BSSA 具有一定的优越性与竞争性。

5 结语

本文主要探讨了在采用T 型传递函数进行离散化的条件下，BSSA 对于求解0-1KP 问题的性能，在未来还可对T 型传递函数的拓展进行测试，并与S，V 型经典传递函数进行比较得出对于BSSA 求解0-1KP 而言最优的传递函数，同时也可将BSSA 用于其他二元优化问题。