基于改进证据理论和多神经网络融合的故障诊断方法

2022-09-09邓丽君

电子技术与软件工程 2022年12期

邓丽君

（湖南高速铁路职业技术学院铁道电信学院湖南省衡阳市 421001）

在液压系统故障诊断中，单源故障诊断信号具有模糊性、不确定性，难以得到系统发生故障时全面的故障状态信息。因此，需要对多传感器信息进行综合分析和处理，才能实现全面而准确的故障诊断。D-S(Dempster-Shafer)证据理论在处理不确定性问题方面具有非常大的优势，目前在故障诊断和目标识别等诸多领域得到了广泛的应用。然而，D-S证据理论在处理高冲突证据时，得到的结果常常有悖常理。本文从各个证据本身重要性不一致出发，遵从少数服从多数的观点，提出了基于证据权重的证据合成新方法。用算法获得各证据间的距离值作为证据本身的权重系数，再利用新的证据合成公式将修正后的证据体组合而得到结果。

BP算法的人工神经网络模型可以看作是故障诊断中的模式识别，且BP神经网络具有很强的自学习、自适应和容错能力。本文结合D-S证据理论和BP神经网络两者的优势，提出了基于改进证据理论和多神经网络融合的故障诊断方法。最后，将该方法应用于液压系统柱塞泵的故障诊断中，将多源故障参数提取特征参数后构造相应的子神经网络分类模块，利用本文所提出的证据合成方法和神经网络结合实现对故障的准确诊断，结果显示了所提出方法的合理性。

1 基于证据权重的证据合成新方法

1.1 D-S证据理论

D-S证据理论又称为Dempster-Shafer理论，它是于20世纪60年代由Dempster最早提出的，其学生Shafer在他的基础上于1976年对该理论进行了改进。它由一系列互不相容的基本命题组成，称为辨识框架Θ，记为{x,x,...,x}。Θ中的子集是由某个问题可能出现的所有答案组成。

定义1 设Θ为一辨识框架，如果集函数m：2→[0,1]符合下列条件：

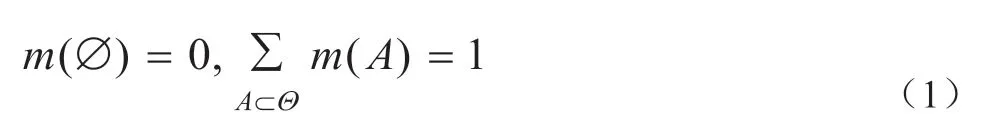
图1：信度函数曲线图

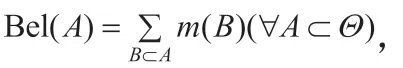
定义2 设m,m,...,m是同一辨识框架Θ上的基本概率赋值，合成后的基本概率函数m：2→[0,1]如下：

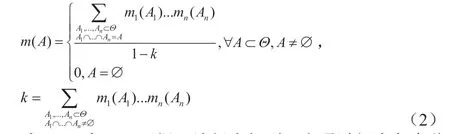
式（2）为D-S证据理论组合规则，它通过组合各个独立证据，从而获得更完备的证据信息。式中，k是冲突因子，证据之间的冲突程度大小可以由K值来反应。

1.2 基于证据权重的证据合成新方法

为了解决高度冲突证据的融合问题，国内外学者提出了许多改进算法，归纳起来主要是如下两类：第一类方法主要是基于对D-S组合规则本身进行的修正，以此来解决冲突证据的再分配问题，代表学者有：Yager、孙全和李弼程。第二类方法主要是基于对证据源本身进行的修正。该类方法的首先提出者是Haenni，其他学者有叶清和蒋雯等。

在实际诊断系统中，由于人为或者环境因素等的影响，会出现个别或者少数冲突证据的出现，从而影响了诊断结果的准确性。本文从不同证据本身重要性不一致出发，遵从少数服从多数的观点，利用算法获得证据间的距离，得到代表证据重要程度的权重系数对证据进行预处理，再利用D-S组合规则进行融合。

在信息融合系统中，设辨识框架Θ={A,A,...,A}，证据集E={E,E,...,E}，各证据源对应的基本概率函数为m,m,...,m，在证据合成公式中加入证据权重系数，计算步骤如下：

（1）考虑到证据本身的相关性，定义一个能衡量证据体之间相似度的欧式距离函数：

计算得出函数值越小，说明两个证据之间相似度高，冲突小，反之，则两证据体冲突大。

（6）将经过修正后的证据使用式（2）的证据理论组合规则进行融合，从而获取可靠的结果。

改进的D-S证据合成方法，继承了D-S组合规则的优点，从证据源本身着手出发，赋予各证据一个表征重要程度的权重系数，算法易于理解，步骤简单，合成结果的可靠性和准备性更高。

2 基于改进证据理论的多神经网络融合故障分类模型

BP神经网络是按误差逆传播算法训练的多层前馈网络，其人工神经网络模型可以看作是故障诊断中的模式识别，且BP神经网络具有很强的自学习、自适应和容错能力，但是如果输入的样本数据太大，输入输出关系复杂，就会导致BP网络训练时间长且慢，甚至网络不收敛。为了解决这个问题，从人脑各区域分工处理信息着手，将每个传感器采集到的信息分别建立一个子神经网络模型进行特征参数空间到故障空间的映射，简化神经网络结构。并将这些子网络的初步诊断结果作为一个证据体，利用提出的改进证据理论合成方法进行修正后再次融合，得到诊断结果，因为最终诊断结果为各子神经网络共同作用下所得，所以准确度更高，各子网络的分别诊断，提高了故障分类速度和精度。

本文提出的故障诊断方法，将改进D-S证据理论方法与BP神经网络的优势相结合，其故障诊断模型如图2所示，诊断分为两层：局部诊断层和决策诊断层。

图2：基于改进证据理论和多神经网络融合的故障诊断模型

2.1 基于子BP神经网络的局部诊断层

首先，对从故障系统采集的各传感器故障信息进行预处理，构成各传感器的特征子空间；其次，根据特征子空间，构建用于诊断的子BP神经网络分类模块，并初始化相应的参数，例如每个网络的输入层、隐含层和输出层的节点数，训练目标等；然后，每个网络通过学习样本来学习训练；最后，对每个训练好的子神经网络，利用相应的测试样本集进行测试，得到各子BP神经网络的性能参数。

2.2 基于改进D-S证据理论的融合决策诊断层

各子神经网络分类模型进行局部诊断后，其输出作为证据体E，用新的D-S证据理论合成方法修正后，进行再一次融合后得到诊断结果。算法流程如下：

（1）根据故障系统出现的故障状况可能发生的故障来确定故障集，即辨识框架Θ。设Θ={A,A,...,A}，各子神经网络训练的故障模式与辨识框架的一致。

（2）确定证据体。各子神经网络局部诊断后的结果构造证据体。

（3）获得各故障模式的基本可信度分配。用如下公式对各子神经网络的局部诊断结果进行归一化处理，得到各故障模式的基本可信度分配值：

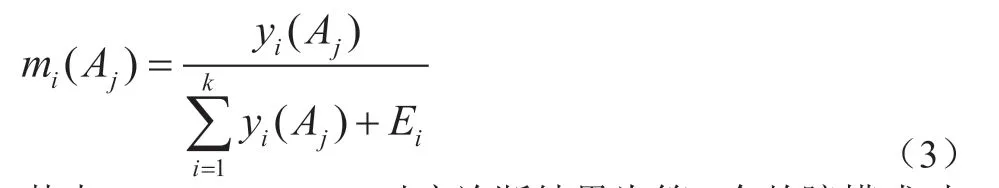
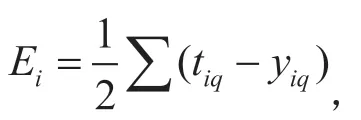
（4）新算法组合各证据。各个故障模式的最终可信度分配和不确定度m(Θ)通过用新的D-S证据理论合成方法对预处理后的局部诊断结果进行计算和融合而获得。

（5）决策诊断。对步骤（4）得到的各个故障模式的最终可信度分配和不确定度m(Θ)，最终诊断结果A通过以下3个判别规则得出：

规则1

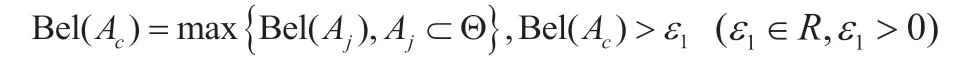
规则2

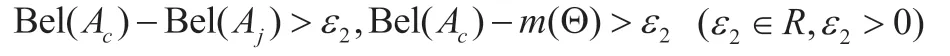
规则3

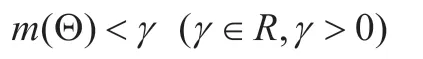
需要注意，ε、ε和γ的值是根据诊断系统的实际情况预先设定好的阈值，最终所得的诊断结果必须同时满足以上3个规则，才能是最终判决结果。

3 诊断实例

为了验证上述诊断方法的有效性，本文对液压系统柱塞泵的典型故障用MATLAB程序进行了试验仿真。从众多典型故障中选择4种常见的故障构建了辨识框架Θ={A,A,A,A,A}，5种故障模式分别是脱靴故障、缸体与配流盘磨损、轴承表面损伤、柱塞与缸体间磨损以及正常工作状态。多传感器进行信号采取时，主要选取如下3个部位的故障参数：液压油油温、泵出口压力脉动信号和泵壳振动信号，特征子空间由从检测点采集的参数中提取的峰值、均值、脉冲指标、裕度指标和崤度指标5个特征参数组成，构造3个局部诊断子神经网络N,N,N，其输出为证据体E、E、E。选取20组数据作为故障样本，对每个3层BP子神经诊断网络进行训练，训练次数为100次，训练目标为0.01。经过反复训练后，最终神经网络确定为5-8-5、5-8-5、5-10-5。经过网络训练后，网络收敛速度非常快，误差精度符合预先设计的要求。然后选取10组测试样本对各网络进行测试，将各子神经诊断网络的输出作为证据体，利用公式5算出每个故障模式的基本概率分配，利用本文提出的证据合成方法对证据进行修正后进行再一次融合，得到最终诊断结果。由于篇幅有限，这里仅给出了在A故障模式下3组数据分别通过3个子神经诊断网络单独作用下的基本可信度分配和诊断结果，如表1-3所示，利用本文的证据合成方法融合后的结果如表4所示。

表1：子神经网络N1的局部诊断结果

表2：子神经网络N2的局部诊断结果

表3：子神经网络N3的局部诊断结果

表4：改进的证据理论对局部诊断结果的融合诊断结果

在这个故障诊断系统中，我们取ε, ε=0.3，γ=0.1，对表中各诊断结果通过3个判决规则分析可知：表1中，对于第1组数据，Bel(A)=0.4713，Bel(A)=0.2897，

Bel(A)=0.1898，(0.4713-0.2897<ε, 0.4713-0.1898<ε)，第3组数据中，Bel(A)=0.5278，Bel(A)=0.2622，(0.5278-0.2622<ε)，它们均不满足判决规则2的要求，诊断结果不正确；表3中，对于第2组数据，Bel(A)>Bel(A)，诊断结果有误，可以判断此证据为冲突证据，在证据融合过程中的影响应较低，权重较小。在表4中，各传感器诊断结果一致，满足3个判别规则的要求，但是故障模式的可信度较低，如果有多个故障同时发生时，也可能会出现表1和表2中的情况，导致系统的故障状态无法正确判断。而表5中利用改进的证据理论合成方法对各个子网络的局部诊断结果进行修正并再一次融合后得到了正确的诊断结果，故障模式的可信度高，不确定度接近0。可知，对单源故障诊断信号进行诊断，因难以得到系统发生故障时全面的故障状态信息，诊断结果可信度低，不确定性高，无法准确判别故障状态。而对多传感器信息采集的各故障信号进行综合分析和处理，诊断的可信度和精度大大提高，能实现全面而准确的故障诊断。同时，本文提出的证据合成新方法，解决了证据冲突问题，降低决策的不确定性，大大提高了诊断的精度，实现了对液压系统故障的准确诊断。