结合去趋势的AR模型变形数据预测

张京奎 王星星 陈永昌

（卫星导航系统与装备技术国家重点实验室 河北省石家庄市 050081）

1 引言

由于工程设计并不能完全准确的估计工作条件及参数，而施工质量也难以做到完美无缺，因此，变形监测作为保证安全的有效措施，贯穿工程施工建设期，甚至在运营期长期进行。变形预测作为变形数据分析的主要内容，主要是通过对获取数据的规律预测未发生的变形，以对未来是否发生危险进行初步判断，并作为制定相应措施的参考依据，达到降低损失和保障安全的目的。随着科技与全球定位系统的发展，变形监测手段从传统的方式发展到利用空间卫星技术的方式进行，空间方式主要是采用全球定位系统GNSS(Global Navigation Satellite System)进行监测，上世纪八十年代，国外开始使用技术建立地壳形变监测网，为地球动力学、地震与火山喷发等研究服务。从九十年代起，我国先后建立多个全国性的监测网和区域性监测网，并进行了重复观测和连续观测，利用这些资料建立了中国大陆及周围地区的地壳运动速度场，给出了中国大陆地壳水平运动的基本特征，由于GNSS具有全天候、全球性、高精度，同时人工干预少等特点，目前在室外建筑物、桥梁等的监测方面经常被采用，室内由于接受不到卫星信号，它的使用受限，故监测隧道等通常采用地面常规测量技术全站仪配合水准仪的方式（传统测绘）、特殊和专用的测量手段进行。变形预测方法的研究已经取得较为丰硕的成果。其中，许国辉等采用AR模型对大厦沉降变形数据进行建模预测，并改进了检验方法，得到了较好结果；陆付民结合卡尔曼滤波建立改进模型，并对链子崖危岩体变形数据进行建模拟合，证明了改进模型拟合效果更好；高宁等将建筑变形波动数据分为趋势项和随机项，以优化参数的GM(1,1)模型预测趋势项，而以AR模型预测随机项，实例验证效果较好；李克昭等、孙国凯等对GM(1,1)模型与马尔科夫模型相结合进行变形预测进行了研究且实例验证了模型可行性，并基于工程实例，对不同模型下隧道围岩位移的预测预报数据进行对比分析，结果表明，GM-MC预测模型在对围岩位移的预测中优于GM(1,1)模型，与实测值有较高的吻合度，能满足工程实际需求；甘祥前等采用GM(1,1)模型预测趋势项而以整体最小二乘求参的AR模型预测随机项，并以三峡库区某高边坡实测数据验证了模型；容静等结合卡尔曼滤波建立GM(1,1)-AR模型并行边坡变形预测；杨帆等将自记忆原理与GM(1,1)模型相结合，建立自记忆灰色模型，并应用于高层建筑沉降预测中。然而，以GM(1,1)模型实质是以指数函数进行预测，预测结果单调，而AR模型适用于趋向于平稳的预测。为了避免趋势项未必单调的影响，本文将原始数据序列进行变换生成围绕零附近上下波动的新序列，而新序列满足AR模型建模条件，以AR模型建模预测，然后对预测结果进行还原，得到累计变形预测值。经实例验证，短期预测结果较好。

2 预测模型

2.1 原始数据序列变换

设原始数据序列为X=(x(1),x(2), …,x(n))，构建二维平面点序列(i,x(i))(i=1,2, …,n)，取序列中相邻三点数据，计算中间点至两端点连线的垂距，设为h，则可得到垂距序列，序列任一元素h计算公式为：

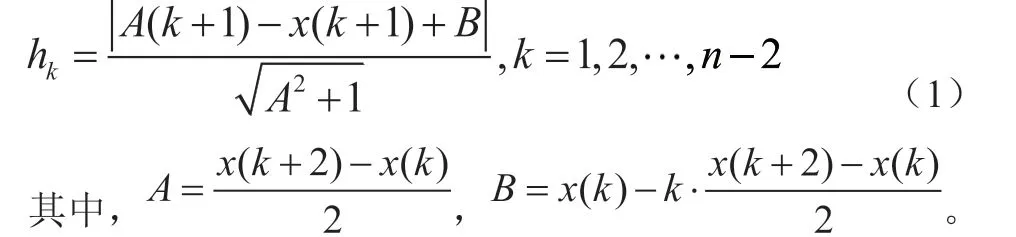
其计算示意图如图1所示。由公式（1）可计算得到垂距大小，但由于数据存在波动，为了呈现数据的波动，对垂距计算值序列定义正负，以表示原始序列所连折线的凹凸，定义正负后所得新序列定义为Y=(y(1),y(2), …,y(n-2))。则：

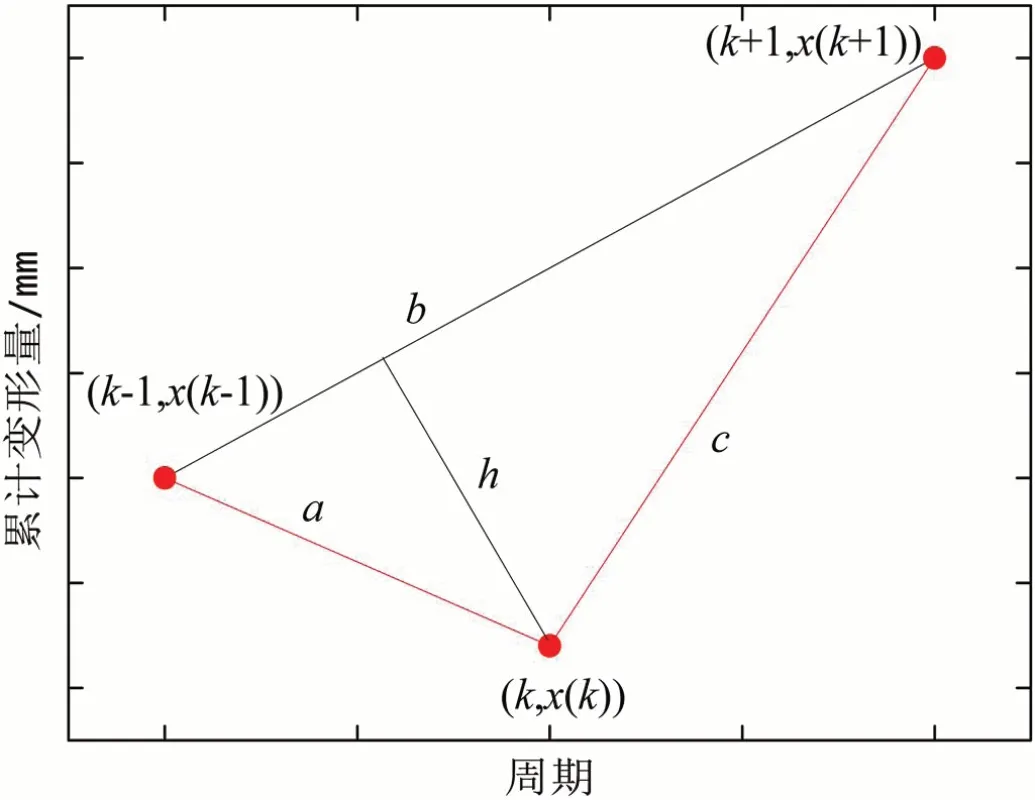
图1：数据变换及还原示意图

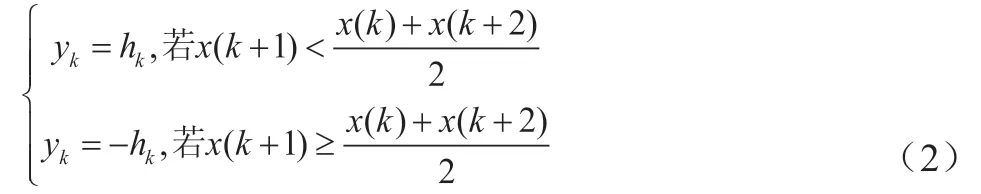
2.2 AR模型建模

自回归模型（Autoregressive Model，简称 AR 模型）是最常见的平稳时间序列模型之一，在变形监测数据分析过程中经常被采用，一般用于描述平稳随机过程。该模型是用序列过去或滞后值表示当前值。若一个时间序列可利用其滞后数值线性回归，则为自回归过程，之所以称为自回归，也是由于自变量与因变量是相同的，是因变量以前时期的数值。其一般表达式为：

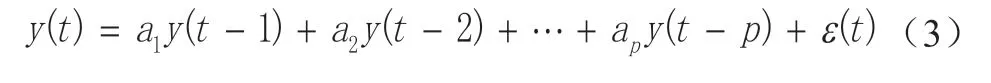
式中，y(t)为时间序列，p为模型阶数，a为自回归参数，表明改变过去一个数值时对y(t)所产生的影响，是根据样本观测值估计的参数，ε(t)为噪声。

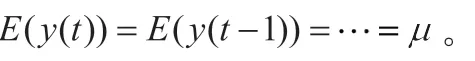
在应用中，自回归时间序列的阶数是未知的，需要根据实际情况来确定。其确定方法可以采用两种方法：一种是利用偏自相关函数(PACF)；另一种是利用信息准则函数。

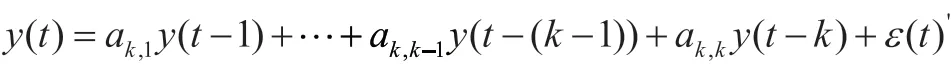
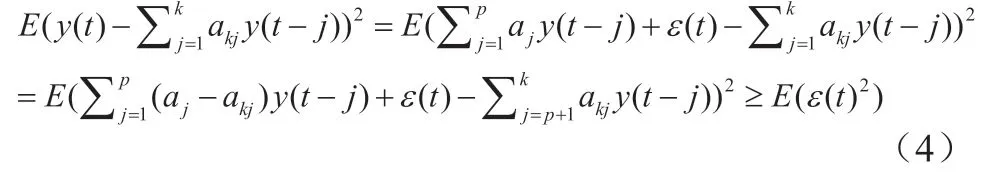
在假设ε(t)与y(t-j)不相关的情况下，等号成立，当且仅当

这表明，AR(p)的偏自相关系数在p步之后截尾。因此，对于p阶自回归模型的间隔为p的样本偏自相关系数不应为零，且对所有j>p， 应该接近于零，则可以利用这一性质来确定自回归模型的阶数。

有时候选择偏自相关函数确定模型阶数可能并不成功，也相对复杂。则可以考虑采用信息准则函数方法。自回归模型的阶数应该使得信息准则的数值达到最小。而对于信息准则，多采用赤池信息准则(AIC)和苏瓦兹贝叶斯准则(SBC)。其可分别表示为：

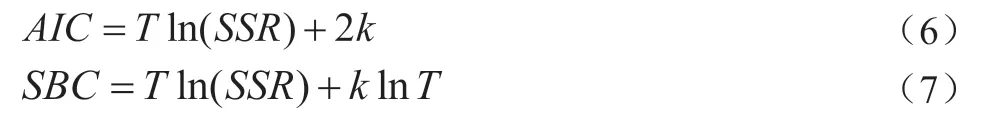
其中，SSR表示残差平方和；k=p+q+1表示待估计参数的总个数，若不含常数项，那么，k=p+q；T表示样本容量。可以通过添加滞后项使得AIC(或SBC)达到极小值，即AIC(或SBC)越小表示模型越好，则阶数选取越好。

对于自回归模型的参数估计主要有三种方法分别是：矩估计、最小二乘估计和最大似然估计，本文采用最小二乘法进行估计，下面主要介绍最小二乘方法参数估计的模型。

对于样本序列{x}，当j>p+1时，记白噪声ε的估计为：

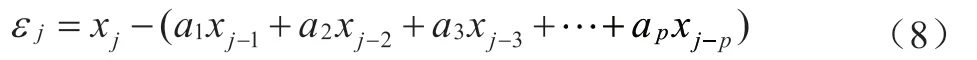
通常ε为残差。我们的优化目标是当j=p+1,……N时残差的平方和达到最小值，具体公式如下，

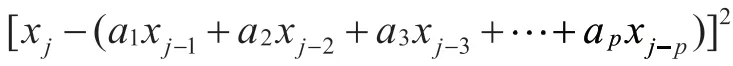
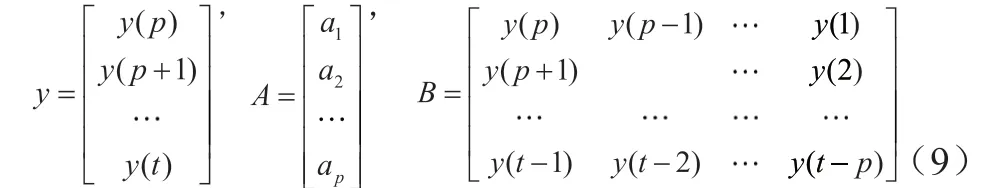
得到线性方程组y=BA+ε，根据最小二乘原理，可求解

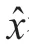
在假设ε(t)与y(t-j)不相关的情况下，等号成立，则可得预测模型为：

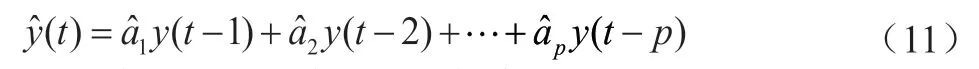
由公式（3）和公式（4）所得序列Y=(y(1),y(2), …,y(n-2))，对其进行AR模型建模，并进行预测。

2.3 预测数据还原

设由公式(11)所得预测值为y(k)，其对应点分别为(k-1,x(k-1))、(k,x(k))、(k+1,x(k+1))，则对应垂距即为y(k)绝对值。如图1所示，根据几何关系可得到公式：

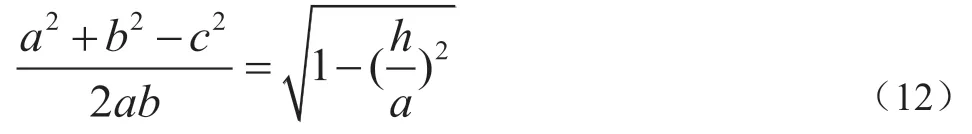
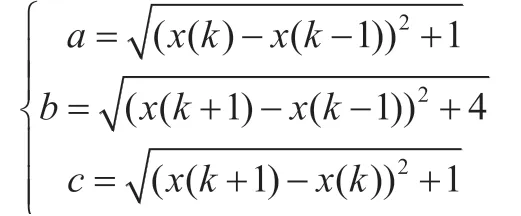
其中，x(k+1)为未知待求量，根据公式（6），采用数值计算的方法，程序求解，可求得两个解。根据y(k)的正负以及公式（2），可求得最终唯一值，即为原始序列X的预测值，在对AR 模型识别时，根据其样本偏自相关系数的截尾步数，可初步得到 AR 模型的阶数 p。然而，此时建立的 AR(p) 未必是最优的。一个好的模型通常要求残差序列方差较小，同时模型页相对简单，即要求阶数较低。因此我们需要一些准则来比较不同阶数的模型之间的优劣，从而确定最合适的阶数，本文采用最优预报准测（Final Prediction Error），简称FPE准测进行阶数的确定，其判断依据为最终预报误差最小，有前文所述AR(p)为拟合模型，γ, γ, …,γ是序列的各阶样本自协方差函数，其最终预报误差公式如下：

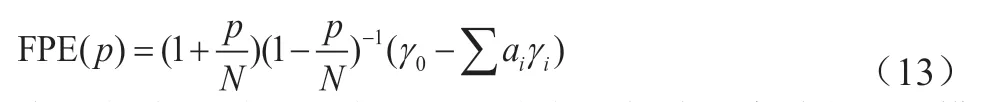
在具体应用时，通常是分别建立从低阶到高阶的AR模型，并计算出相应的 FPE的值，由此确定使 FPE 达到最小的p值。

3 实例分析

实例1 选择菠萝山隧道变形监测数据进行验证。菠萝山隧道是一座连拱隧道，位于洱海东岸，隧道全长为265米，最大埋深约为45米，属于剥蚀构造低中山地貌，出露地层地表为由黏性土、角砾和碎石组成的第四系坡残积，厚度为5～27m，下伏奥陶系下统向阳组一段石英砂岩夹泥岩，隧道围岩为V级，稳定性较差，以前17期实测数据为建模数据，预测后5期数据，并与原文献方法及实测数据比较分析。建模数据序列如表1 所示。

表1：实测建模数据序列

通过相邻三点计算垂距构造新数据序列，则原始时间序列经过计算后获得的新序列有所缩短，新序列是由15期数据构成，是位于区间(-0.45,0.45)的围绕零值变化波动的序列，可以认为是平稳随机序列并采用AR模型建模。原始序列与生成序列折线图如图2所示。

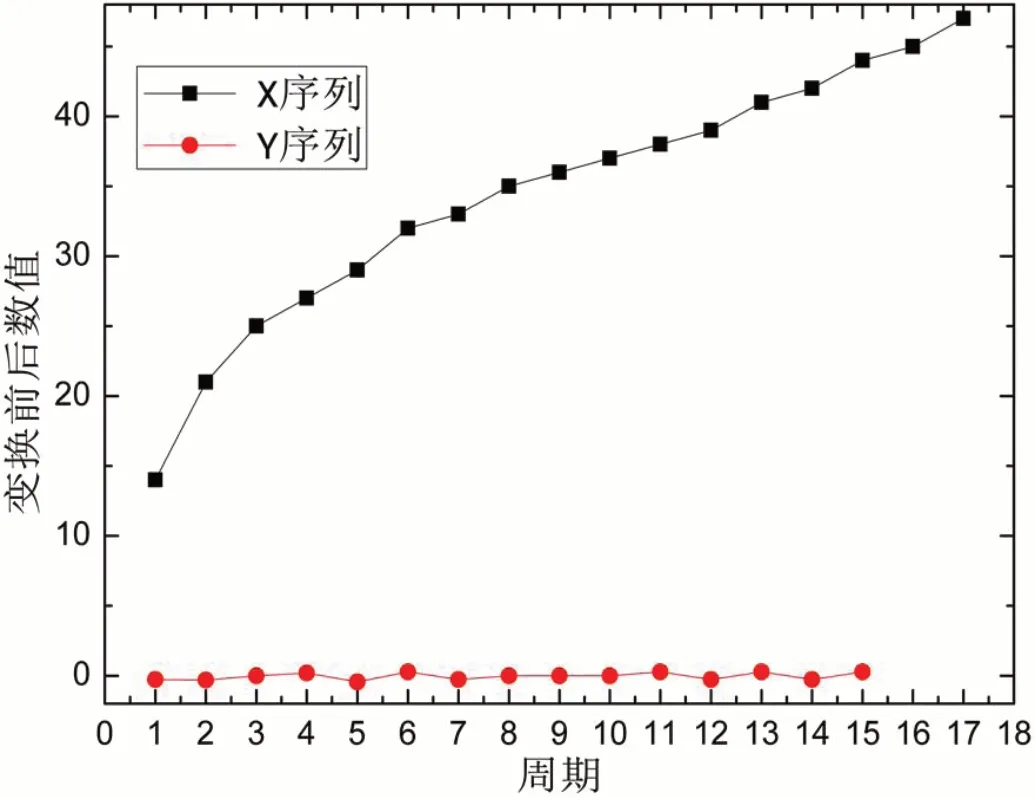
图2：变换前后数据序列曲线

采用AR模型建模预测并将预测数据还原，之后将还原后数据加入至建模数据序列，再次进行预测，从而达到多期预测的目的。其后5期的预测数据与实测值及原文献方法的预测值进行对比，结果如表2所示。

表2：实测值及预测值比较

分析表2可知，第18期、第19期以及第20期预测数据的预测精度与原文献方法预测精度相近，预测残差较小，而第21期与第22期预测数据较原文献方法预测精度差，预测残差均大于1mm，较前3期预测值精度明显降低。其原因在于AR模型在进行自回归时，后期数据出现不按前期规律变化的突变情况，预测误差较大，而其预测误差通过公式计算传递至累计变形量，可能出现放大效果，从AR模型预测结果还原为累计变形值的计算公式可以看出，第21期预测值的精度影响了第22期预测结果。

实例2 选取郑州某时代广场工程楼实测累计沉降数据，其是依据监测要求，布设水准网和监测点，采用徕卡DNA03电子水准仪按照二等水准测量方法进行观测获取的数据。选取其39期观测数据，以前34期数据建立模型，预测后5期。其建模数据如表3所示。

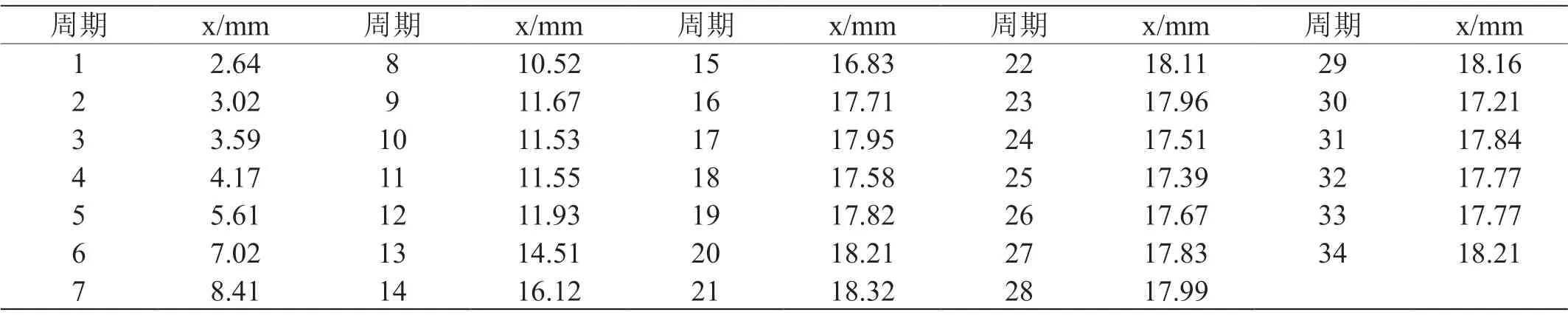
表3：实测建模数据序列

通过相邻三点计算垂距构造新数据序列，则原始时间序列变化后有所缩短，所得新序列是由32期数据构成，是位于区间(-0.79,0.58)的围绕零值变化波动的序列，可以认为是平稳随机序列并采用AR模型建模。原始序列与生成序列折线图如图3所示。

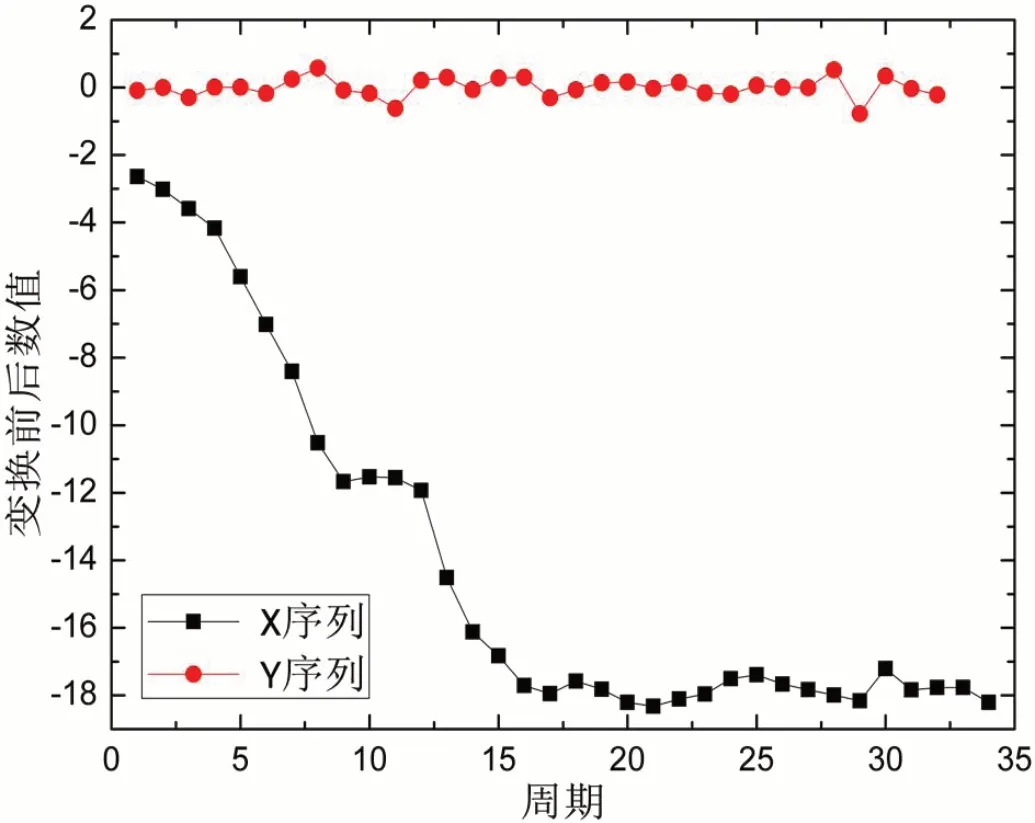
图3：变换前后数据序列曲线

采用AR模型建模预测并将预测数据还原，之后将还原后数据加入至建模数据序列，再次进行预测，从而达到多期预测的目的。其后5期的预测数据与实测值进行对比，结果如表4所示。

表4：实测值与预测值比较

分析表4可发现，其35期至39期数据预测结果较好，残差值均在0~1mm之间，相对误差只有第38期预测值大于5%，而其余预测值均小于5%。而原文献灰色自记忆模型预测结果残差在2mm内。因此认为本文方法在短期预测效果，能够达到与原文献模型预测相同的精度要求。

4 结论

变形监测数据时常呈现波动形式，给变形数据分析及预测带来困难。本文采用相邻三期数据在二维平面坐标系中计算垂距的方法构造新数据序列，对所生成的新数据序列采用AR模型进行建模预测，然后还原为累计变形预测值，并采用AR模型对新序列进行预测并还原为累计变形预测值。该方法直接提取波动随机项进行预测，而对于趋势项并无要求。经过实测数据验证，在短期变形数据预测中，预测结果较好。但该方法依然存在自回归难以应对突变及数据还原误差传递问题，有待进一步研究解决。