基于心智模型发展的进阶教学
——以“向心力”概念教学为例
2022-09-08苏州大学物理科学与技术学院215006王蕾周丽萍
苏州大学物理科学与技术学院(215006)王蕾 周丽萍
物理概念是对物理现象的本质属性和共同特征的抽象概括,学生基于先前认知水平,通过观察分析物理过程、抽取本质影响因素,进行定性定量的推理和检验,最终形成符合事实的“概念模型”。教师在教学准备时多偏重学科知识的层次架构,在教学过程中多关注学生形成概念模型的正确性,而未全面兼顾学生内化概念时头脑中自我理解的转变,忽视整体教学需要的思维引导和衔接。也正是因为学生和教师之间缺乏“共感”,教师对学生建立模型过程的内在表征和动态认知不甚清楚,若教师无法及时回应学生的反馈,学生也就无法建立起清晰完整的物理模型。
建构主义强调,学习是以原有经验为基础,对新旧经验进行反复的意义建构,自主将新知识融合到自身认知结构中。学生在不同阶段表现出的心智模型各有差异,因此运用学习进阶理论规划整体教学活动时,教师要以学生的心智模型发展规律为依据,关注学生的动态建模过程,顺势给予思维指引,确保每一层次的进阶深化都有助于学生完善自身的科学模型。将学习进阶的阶点设计与学生心智模型表征状态相结合,既围绕核心概念逐级进行深化,又贴合学生的主观理解,使物理课程成为组织化的有机整体。本文将基于学生的心智模型发展规律,对“向心力”的概念教学进行进阶设计,以提升学生的科学思维能力。
一、理论简介
(一)心智模型
心智模型最先由肯尼斯·克雷格(Kenneth Craik)提出,是指个体对真实世界构建的“小型模型”[1]。美国在2012 年颁布《K-12 科学教育的框架:实践,跨学科概念与核心概念》中,强调了心智模型在学科概念中的作用,并将其写入课程文件[2]。心智模型是个体经验与外在情境的交互,是对事物形成内在认识的结果,它在一定程度上展现了个体解释事物的思维细节。学生通过观察和感知建立的初始模型可能是基于经验建立的缺陷模型,不可避免会出现非科学化的特征,关于核心概念的知识掌握处于碎片化状态。心智模型是学生主观建立起来的,个体面对客观复杂的物理情境时,需要抽取反映事物或现象的本质因素和参数,修正原先存在缺陷的模型,并不断调用进阶后的心智模型解释、验证和预测新情境,最终将心智模型转变为稳固化的科学模型。学生建模的过程体现了学生思维加工的方式,对物理概念、规律、现象、公式等的理解都需要心智模型参与,学生外显的心智模型是教师动态调整教学策略的依据。
(二)学习进阶
美国国家理事会(NRC)认为,学习进阶是“在学生探究某一知识领域时,对学生产生的连贯且逐级深化的思考认识的描述”[3]。郭玉英团队围绕此开展了系列研究,认为需要提供“阶”来支撑学生对核心概念的理解,设计教学路径要为学生架设认知点,根据学生原有知识经验和思维水平确定进阶起点,根据教学目标和核心素养预设进阶目标,以学生认知发展关键点为依托划分进阶层级,确定概念理解衔接的“阶点”[4]。物理知识复杂度的提高对学生知识整合能力提出了更高的要求,将学习进阶理论应用到概念教学设计和实践中,有助于学生对概念建立结构化理解,促进学生心智模型的层级发展,进一步实现教学路径与学习轨迹结合。教师在学习进阶理论框架下,根据学生的心智模型发展规律判断进阶“锚点”,规划进阶教学的范式,让学生主动科学化心智模型,建构自己对概念的理解。
二、关于“向心力”概念的学习进阶分析
进阶教学首先要判断学生的预备知识和能力水平,“向心力”一节是牛顿第二定律在曲线运动中的应用,体现匀速圆周运动的动力学特征,对学生的理解能力和分析综合能力要求较高。在学习向心力之前,学生头脑中已经存在有关匀速圆周运动的情境实例,并能根据物体的运动状态进行受力分析,能够应用牛顿第二定律建立映射关系,同时学生已经了解匀速圆周运动中各特征参量的物理意义。但各个知识点在学生头脑中处于分离状态,学生对匀速圆周运动的认识仍处于初级阶段。
教师围绕“运动与相互作用观”的核心理念展开教学活动,通过创设情境、提出问题引导学生建构完整的概念单元。在知识层面,学生达到能理解向心力概念和影响向心力大小因素的水平,可以归纳总结物体做圆周运动的性质和条件,能运用公式对圆周运动的动力学问题进行分析求解;在能力和方法层面,学生通过收集证据、推理论证、建立模型等过程,提高分析问题和解决问题的能力。笔者根据预设的进阶目标,设计如图1 所示的“向心力”教学进阶框架[5]。

图1 “向心力”教学进阶框架
三、基于学生心智模型发展的“向心力”进阶教学设计
为了引导学生将不完善的心智模型整合成体系化的科学模型,教师在教学活动中要以学生思维进阶的关键点为依托,通过具体物理情境使学生心智模型充分外显,积极促进学生抽象逻辑思维能力的发展,将科学方法内化为学生自身的思维方式。本文将从以下几个方面设计“向心力”一节的教学活动。
(一)准备起点知识,创设问题情境
【教师演示】教师在开口水瓶中倒入适量水,用绳子拴住水瓶,制作如图2 所示的简易水流星装置。实验开始前告知学生注意观察水瓶到达最高点时的现象,教师演示水流星在竖直平面内以一定速度做圆周运动。学生发现开口水瓶运动到最高点时,水不会像正常倒置时一样流下。而后教师提出引导性问题:在最高点,开口水瓶处于倒置状态,水却未流出,水所受的向下的力去哪里了?
评析:通过问题导向引发学生探究情境背后物理本质的兴趣,鼓励学生带着问题主动参与教学过程;通过创设情境让学生在头脑中建立匀速圆周运动的初始模型,推动学生继续探究物理现象的本质。

图2 水流星装置示意图
(二)建立感知模型,引导知识延伸
【学生活动】学生观察小球在紧绷细线的牵引下,在玻璃平面上绕图钉做匀速圆周运动的特点,而后用剪刀将细线剪断,观察小球的运动方向(如图3)。

图3 断线小球运动示意图
【问题提升】(1)若忽略小球运动时所受的阻力,分析小球所受的合力以及合力的方向。(2)剪断细线后小球的运动方向如何?(3)小球的线速度大小和方向是什么样的?(4)物体运动状态改变的原因是什么?(5)合力和线速度方向成什么夹角?(6)该合力对物体做功吗?
评析:教师为学生构建可理解的情境框架,通过有层次的问题为学生提供思维进阶的着力点,学生首先能够利用前概念自主对物体进行受力分析,发现小球在细线拉力的作用下做匀速圆周运动,拉力方向指向圆心。剪断细线后,学生发现小球将沿着该点运动的方向飞出去,即线速度方向沿着圆周运动的切线方向。向心力方向始终与速度方向保持垂直,只改变线速度方向,不改变其大小,进一步延伸到向心力不会对物体做功的深度理解。在分析过程中,学生在判断物体的运动状态是否发生变化时,会出现“线速度大小不变,即物体运动状态不变”的迷思概念,教师可以让学生画出圆周轨迹上不同点的速度方向,纠正错误的心智模型。
(三)外显认知冲突,修正心智模型
【学生活动】学生分析下列圆周运动实例,判断向心力的来源,并描述实例中圆周运动的运动特征(如表1)。

表1 向心力来源实例分析
评析:学生画出物体轨道示意图和受力示意图展示自身的心智模型,并与其他同学交流,暴露出不完善的心智模型。学生在最初建立向心力概念时,容易产生“向心力是物体受到的一种力”的错误认识。学生通过自主辨析上述物体的受力情况,认识到向心力是由某种力提供的,而非一种实际受到的力,并能判断出圆周运动的轨道平面、圆心位置和半径等。教师总结向心力是按力的作用效果命名的,并强调它既可以是某几个力的合力,也可以是某个力的分力,反映出“供”与“需”的辩证关系。
(四)建立表征模型,定性定量并行
【学生活动】学生握住拴有沙袋(沙袋质量为m)且长为L的绳子,使其在水平面内以角速度ω做匀速圆周运动,感受绳子拉力F1的大小。而后分别只改变绳子长度为2L,沙袋质量为2m,角速度为2ω时,让学生体会几种不同情况下手握绳子的拉力。结合上述实验活动,学生能体会向心力的大小和物体的质量m、角速度ω、圆周运动半径r之间的关系,感受物体质量m越大、角速度ω越大、圆周运动半径r越大,所需拉力越大,即向心力越大。
【教师引导】教师首先带领学生复习旧知——牛顿第二定律的内容,然后再次强调做匀速圆周运动的物体的运动状态在时刻发生变化,物体始终受到一个指向圆心的力。向心力只改变速度方向而不改变速度大小。学生知道力是物体产生加速度的原因,进而明确物体所受指向圆心的合外力产生的是物体的向心加速度,满足F=ma。最后教师引导学生理论推导向心力公式F=ma=mω2r=。
评析:对向心力公式进行理论推导,既要求学生在知识层面理解向心力公式推导是牛顿第二定律应用的延伸,又考查学生的理论推导能力和逻辑思维能力。基于学生对“影响向心力大小的因素”有一定主观感受,从定性和定量两个角度围绕向心力加工概念,多方面完善学生关于向心力的心智模型,促使学生头脑中的认知点发生联系,提高学生推理概括的抽象思维能力。
(五)检验修正模型,深入内化概念
理论推导出向心力公式后,教师引导学生利用向心力演示器(如图4)探究向心力表达式,匀速摇动手柄使两个钢球做匀速圆周运动,钢球运动所需的向心力由挡板对钢球的压力提供,钢球对挡板的反作用力使筒柱压缩,压缩弹簧露出红白相间的等分标线,根据露出的等分标线可以粗略确定两个球所受的向心力之比。依次通过更换钢球改变m、通过更改皮带的塔轮半径改变ω、通过更改钢球槽位改变r,并保持其他物理量不变,学生分组合作,分别探究各因素对向心力大小的影响[6]。
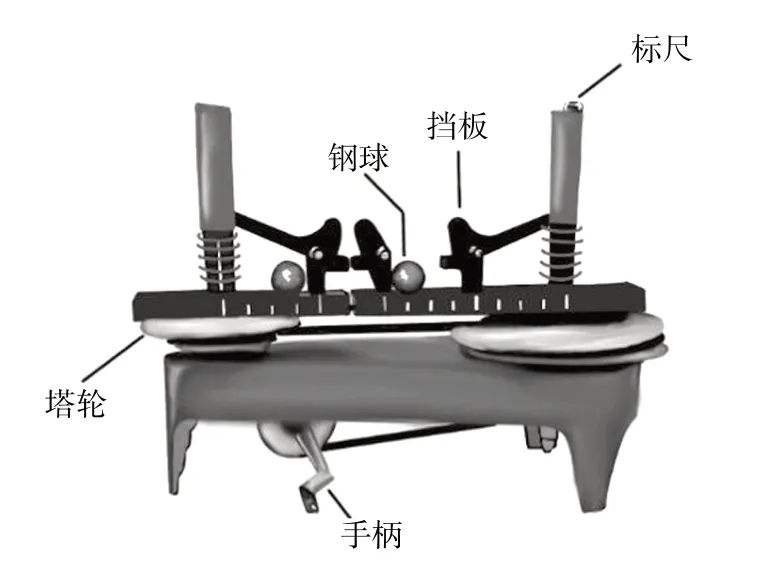
图4 向心力演示器
评析:学生参与实验探究活动,通过观察、测量、记录数据等实验操作,为先前的结论推导提供事实支撑;学生调用心智模型进行验证,主动接纳经过实践检验的概念,同时采用控制变量法自主实验。
(六)整合相关特性,构建概念体系
教师要求学生对学过的匀速圆周运动的相关特点进行归纳,学生总结出:①匀速圆周运动中线速度大小不变,方向时刻改变;②匀速圆周运动中角速度、周期、频率都保持不变;③匀速圆周运动中向心加速度和向心力大小都不变,方向时刻改变。而后教师通过反向设问“质点做匀速圆周运动的条件是什么?”,考查学生是否理解:当质点在受到大小不变、方向始终垂直速度方向且指向圆心的合外力时,物体会做匀速圆周运动,只存在向心加速度。
评析:学生经历感知体验、质疑验证、推理分析等思维过程后,对向心力的概念具有相对完整的认知。教师以匀速圆周运动作为认知结构的固化点,由学生填补匀速圆周运动的各物理量特点、性质以及物体做匀速圆周运动的条件,综合线速度、角速度、周期、频率、向心加速度、向心力等因素构建匀速圆周运动的框架体系,将零碎分离的知识状态联结为有序分层的整体,将原先模糊有缺陷的心智模型转变为科学化的模型。
(七)应用科学模型,全面提升能力
【趣味活动】(1)提供一个高脚杯和塑料小球,如何在手不碰触小球的前提下,将小球移到高脚杯中?(2)如何在只能握住塑料管的前提下,用1 克的乒乓球提起10克的砝码?(如图5)
【问题解答】针对上述问题情境,列出向心力满足的公式。
评析:学生需要对真实的物理情境抽象建模,才能列出研究对象满足的向心力公式。通过趣味活动,学生会利用自己对向心力的理解来解释物理现象和解决实际问题,并运用科学的思维能力进行推理分析,进而深入探求本质,不断迁移反思,形成正确的物理观念。
四、结论
“向心力”的进阶教学安排,以进阶学习理论为指导,分层递进引导学生自主内化科学方法,以现象和实验为依据,帮助学生将知识和经验联系起来,逐步建立科学的概念体系。在此过程中,教师时刻关注学生在内化概念时可能出现的理解误区,通过调动学生主动参与,鼓励学生亲自参与科学探究,修正不完善的心智模型。主观感知和实验探究相结合,定性分析和定量分析相结合,使学生在构建概念的过程中提升逻辑推导、自我反思的能力。在整合应用环节,使学生归纳头脑中的相关知识,整合形成全面的概念体系,面对新的情境能够准确调用模型解释、解决问题,从而提高学生的迁移应用能力。
教师在进行概念教学时,要基于学生本身的进阶起点,包括能力和认知两层面。学生在进阶提升的过程中,教师要重视学生的亲身体验和自主探究。学生在接纳新知识的过程中,需要反复应用、调整心智模型,同时还要得到教师对其错误认知的指导与纠正,只有这样,学生才能逐渐习得科学的思维方法,并将这些方法应用到未来的学习实践中去,提升物理学科核心素养。
