一种长大下坡路段高速铁路再生制动能量的分析方法
2022-09-07章叶心邓云川刘志刚张雨婷陈涛黄可
章叶心,邓云川,刘志刚,张雨婷,陈涛,黄可
(1.西南交通大学电气工程学院,四川 成都 610031;2.中铁二院工程集团有限责任公司电化院,四川 成都 610031)
随着西部大开发的实施,我国大量规划建设渝利铁路、成兰铁路、川藏铁路等复杂山区铁路。其中川藏铁路所经地区地形高差极大,因此设置长大坡度的线路是难以避免的[1]。目前我国动车组制动方式均优先采用再生制动,动车组通过长大下坡路段时所需再生制动力大且制动时间长,会向电力系统返送大量的再生制动能量[2],所以研究高速动车组在长大下坡路段的再生制动过程是很有必要的。
国内外很多学者通过对牵引供电系统和高速动车组进行建模仿真[3-8]来研究高速铁路中返送的再生制动能量的影响。对于牵引供电系统建模,文献[3]建立了单相π型等值电路模型,但模型没有详细考虑牵引网复杂的拓扑结构;文献[4]基于多传输导体理论,利用牵引网各元器件的节点导纳矩阵构建了精确的链式网络模型,但该多端口模型具有矩阵计算复杂、仿真速度低等限制;文献[5]以电力系统平行多导体传输理论为基础给出简化的牵引网多导线模型,对牵引网多端口模型进行了降阶处理。
对于高速动车组牵引传动系统建模,文献[6]建立了电流源及恒功率源等效模型,与动车组的实际情况差别较大,未反映再生制动的工作机理;文献[7]利用仿真软件对动车组的建模中仅搭建了整流器部分,未考虑逆变器-电机调速系统,无法模拟动车组在不同速度下的负载转矩和阻力情况;文献[8]仿真了整个动车组牵引传动系统,能反映各种运行条件下的情况,但未考虑牵引网系统对动车组运行过程中吸收或返送能量大小的影响。
这些研究成果,对牵引供电系统和动车组牵引传动系统的数学模型以及再生制动能量的产生机理做了较全面的阐述。但由于动车组在实际运行过程中,电能流动回路包括复杂牵引网、车顶高压电缆、车载变流器、车体、接地线、钢轨等多个部件,若忽略过多部件会影响电路拓扑结构,从而影响仿真结果的准确度。因此,目前对于高速动车组再生制动能量的研究存在两个方面的不足:1)已有的再生制动模型通常只针对局部电路进行研究,未将复杂牵引网结构、动车组接地部件与动车组牵引传动系统的整流器、逆变器及电机作为整体研究,且未能建立互耦合的仿真模型;2)已有的牵引网-动车组一体化等值电路模型较少考虑长大下坡路段的坡道参数影响,且并未给出制动功率与转子转速的函数对应关系。
鉴于此,本文以我国典型高速列车CRH3型动车组为例,建立了精细的牵引网-动车组耦合电路模型(考虑了复杂牵引网、动车组牵引传动系统及动车组接地系统等部件),并详细考虑了坡道参数的影响。通过拟合制动功率与转子转速的函数关系,对模型目标指令参数进行求解,实现坡道参数与仿真模型的结合。在此基础上,针对不同线路条件下的动车组制动工况进行仿真,分析再生制动能量对牵引网-动车组系统电气特性的影响,并对其电压安全进行评估,以期为线路前期设计提供参考。最后,结合成渝线棉丰-李家湾牵引变电所的实测数据,验证了仿真分析方法的正确性及实用性,并通过比对已有文献可知,本文提供的仿真结果与实际情况更为接近。
1 再生制动原理
再生制动是指高速动车组在减速运行过程中,牵引电动机转变为发电机,同时产生为高速动车组减速运行提供电制动力的制动力矩,并将多余的电能反馈回牵引网的过程[9]。
高速动车组在制动工况下,能量流动过程与牵引工况相反,处于发电状态的牵引电机所产生的电能经逆变器整流为直流电,再经脉冲整流器逆变为交流电后反馈回牵引网,实现再生能量的回馈,如图1所示。

图1 高速动车组牵引传动系统能量流动示意图(1-受电弓,2-变压器,3-整流器,4-逆变器,5-电机)Fig.1 Schematic of energy flow in traction drive system of highspeed EMUs(1-pantograph,2-transformer,3-converter,4-inverter,5-motor)
2 牵引网-动车组系统仿真模型的搭建
2.1 牵引供电系统模型
自耦变压器(auto-transformer,AT)供电方式的复线全并联牵引供电系统结构见图2,其中,牵引变电站主变压器的接线方式采用V/x接线,变比为220:27.5;T为接触网,R为钢轨线,F为馈线,P为保护线。

图2 AT供电方式复线全并联牵引供电系统结构Fig.2 Electrical structure of full parallel traction power supply system under AT power supply mode
图2中,牵引网采用基于链式多导体传输理论的降阶建模方法[6]。构建的链式网络模型由串联子网和并联支路组成,各串联子网中的平行多根传输导体间两两互容、互感,可用π型电路等效,如图3所示。

图3 牵引子网π型等效电路模型Fig.3 The π-type equivalent circuit of traction subnet model
图3中,m为牵引网平行传输导体的数目,设子网中各导体电压、电流分别为U(x),I(x);阻抗、导纳矩阵分别为Z(x),Y(x),可知牵引子网的稳态方程为
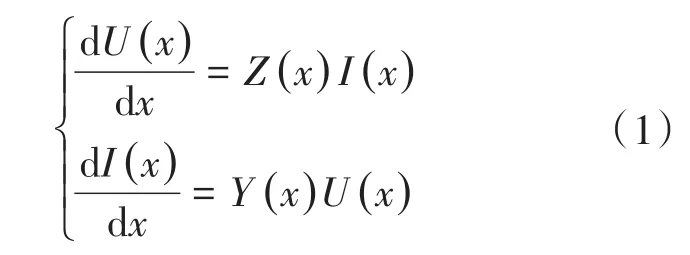
2.2 CRH3型动车组模型
CRH3型动车组的电气结构[10]如图4所示,2号、7号车设有受电弓、车载变压器及工作接地装置,4号、5号车体设有保护接地。在车载变压器的二次侧设有4台变流装置,每台变流装置均包含2台两电平四象限脉冲整流器、1台主逆变器以及4台牵引电机。

图4 CRH3型动车组电气结构示意图Fig.4 Electrical structure of CRH3-type EMUs
图4中,脉冲整流器采用瞬态直接电流控制策略,控制原理如下[11]:
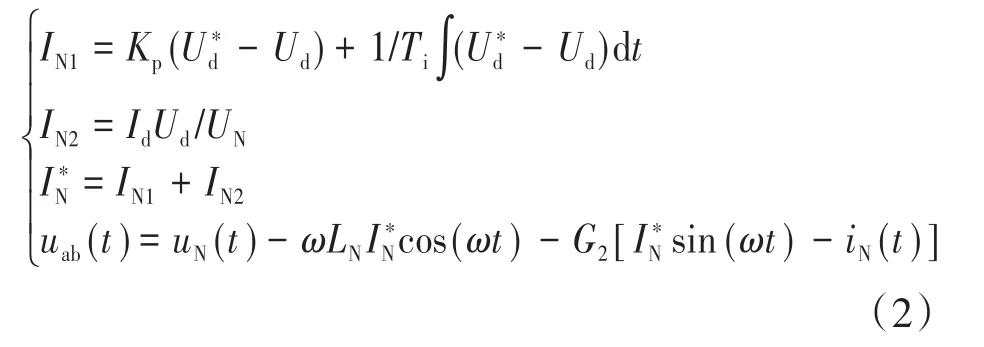
式中:Kp,Ti为PI参数;Ud为中间直流环节电压;Ud*为中间直流侧给定电压,按CRH3车型将其约束在2 700~3 600 V之间;Id为中间直流环节电流;UN为网侧电压有效值1 550 V;IN*为网侧电流给定值;uN(t)为网侧电压瞬时值;ω为网侧电压角频率;LN为网侧等效电感;G2为比例放大系数;iN(t)为网侧电流瞬时值。
牵引逆变器-异步电机系统采用SVPWM调制的电压型矢量控制策略[11],其调速控制原理如图5所示。
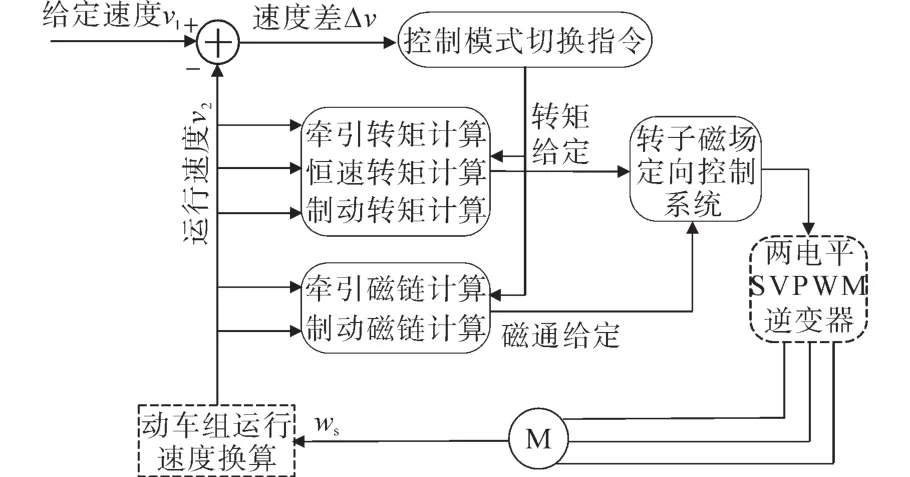
图5 调速控制系统原理框图Fig.5 Schematic diagram of speed control system
根据三相异步电机的工作原理,可知转差率s与转子转速n、同步转速n1关系如下:

若控制电机使n>n1,则电机输出的转矩为负,牵引电机转为发电机状态,此时动车组向牵引网返回电能。因此,动车组模型可通过牵引电机调速系统实现制动工况。
2.3 牵引网-动车组系统模型
将牵引供电系统模块与CRH3型动车组模块按实际的电气耦合关系连接,建立如图6所示的牵引网-动车组系统模型,其中,动车组模块接入距牵引变电所15 km的左供电臂上行线中。

图6 牵引网-动车组系统模型示意图Fig.6 Schematic of vehicle-grid system model
在牵引网链式网络模型中,结合多导体传输线理论以及各导线的几何尺寸、空间位置,利用Carson公式[4]以及静电场镜像法列写出阻抗矩阵和电位系数矩阵,对矩阵进行变换,从而确定导体的感性及容性耦合参数[5]。
对于CRH3型动车组模型,车顶高压电缆的线芯可等效为经验值的阻抗,且线芯与屏蔽层间存在容性耦合,可按π型电路等效;车体与接地装置等效为经验值的电阻;脉冲整流器、逆变器以及牵引电机封装为变流器模块,接在车载变压器的二次侧。根据文献[4-8,11],给出牵引网-动车组耦合模型电气参数,见表1。

表1 车-网耦合模型电气参数Tab.1 Electrical parameters of vehicle-grid model
3 结合坡道参数的分析方法
本节主要讨论结合坡道参数与牵引网-动车组系统等值电路模型的方法,理论分析和仿真思路如图7所示。

图7 结合坡道参数的再生制动能量分析方法流程图Fig.7 Schematic for the analysis method of regenerative braking energy regarding slope parameters
3.1 动车组经长大下坡道运行限速分析
由列车运行控制系统工作原理可知,长大下坡道区段动车组运行速度和坡度、监控制动距离、列车追踪间隔时间以及闭塞分区长度有关。若列车追踪时间超出限值,则需要对动车组进行限速[12]。
闭塞分区长度计算公式[13]为

式中:Lbrake为列车监控制动距离(单位 m);Lprotect为列车安全防护距离,取110 m;Ladd为系统应变附加时间tadd内通过的距离,tadd取13 s;Lblock为闭塞分区长度(单位m)。
列车追踪间隔时间计算公式[13]为

式中:Itrace为列车追踪间隔时间(单位 s);LEMU为动车组长度,取200.67 m;vblock为列车区间运行速度(单位km/h);3.6为单位换算系数。
下面以CRH3型动车组为例,根据列控系统的减速度曲线[14],得到初速度为200 km/h的监控制动距离,代入式(4)、式(5),可计算得相应坡度下的Lblock和Itrace。根据我国高速铁路的实际情况[15],Lblock取 2 000 m,Itrace限值取 3 min,通过图 7所示的试凑法求出相应坡度下的限速值,计算结果见表2。

表2 Lblock=2 000 m,Itrace<3 min的不同坡度限速检算表Tab.2 Speed limitation for different slopes when Lblock=2 000 m and Itrace<3 min
3.2 动车组经长大下坡道运行受力分析
假设动车组在长大下坡路段的运行方向为正方向,视其为单质点,可知动车组受基本阻力、坡道附加力和制动力的作用。
其中,CRH3型动车组单位基本阻力[14]为

式中:v为动车组运行速度(单位km/h);w0为单位基本阻力(单位N/kN)。
坡道单位附加力的计算公式[14]为

式中:i为动车组所处坡道坡度的千分数(‰);wi为坡道单位附加阻力(单位N/kN)。
CRH3型动车组最大常用电制动力特性曲线函数如下[14]:

式中:Be为一个编组所提供的制动力(单位kN)。
设动车组处于坡度为i‰的路段且以速度v恒速下坡,动车组受力分析如图8所示。

图8 动车组受力分析图Fig.8 Force analysis of EMUs
由图8可知,动车组以恒速v下坡时满足:

式中:M为动车组质量,取为5 000 kN;Bi(v)为动车组恒速运行所需的制动力(单位kN)。
根据表2中不同坡度下的限速值,将其代入式(8)、式(9),分析当动车组只施加再生制动力时能否以恒定限速通过长大下坡路段,计算结果如表3所示。

表3 Itrace<3 min的恒速运行所需制动力Tab.3 Braking force required for constant speed when Itrace<3 min
由表3可知,坡度为-32‰以下时,动车组以恒定限速运行所需的制动力均小于最大电制动力,因此只需施加再生制动力即可。
3.3 制动功率与转子转速的拟合
基于3.2节的分析结果,可计算动车组轮周处所需制动功率:

式中:F为所需制动力(单位kN);v为动车组运行速度(单位km/h);P为所需制动功率(单位kW);3.6为单位换算系数。
假设每台异步电动机消耗或产生的电能均一致,故单台异步电动机转子转速为

式中:Ω1为单台电机转子角速度(单位rad/s);Te为单台电机输出转矩(单位N·m)。
单台电机输出转矩由下式计算[16]:

式中:m1,p,f,U1分别为定子绕组的相数、极对数、频率、相电压;x1σ,x'2σ分别为定子绕组的电阻和漏抗;r1,r'2为转子绕组的电阻和漏抗归算值;s为转差率;C为校正系数。
结合式(3)、式(12)可知,电机的输出转矩与转子转速呈正相关,按梯度设置电机转子的初转速值,通过仿真可得制动工况下各转子转速对应的输出转矩大小。由于再生制动时电机输出转矩为负值,为便于分析取其绝对值。利用Matlab拟合出|Te|与Ω1的函数关系曲线,如图9所示。

图9 |Te|与Ω1函数关系拟合结果Fig.9 Fitting results of the relation between|Te|and Ω1
|Te|与Ω1的三次多项式拟合函数为
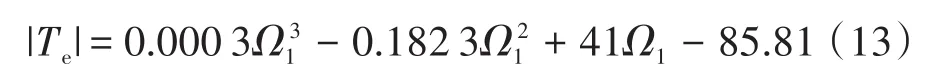
由式(10)可知,Ω1与P的近似函数关系为

综上,将3.1,3.2节检算的限速值与所需制动力代入式(10)、式(14),可计算得不同坡度下对应的转子转速计算结果,如表4所示。根据发生制动前电机正常运行时的功率值,结合式(11)可计算出各异步电机相应的负载转矩,可先暂设负载转矩为500 N·m。

表4 不同坡度下对应的转子转速计算结果Tab.4 Results of rotor speedunder different slopes
3.4 再生制动工况下仿真结果分析
对全长20 km的工程案例进行仿真分析,首先以坡度为-32‰路段为例,通过设置模型的目标速度指令进行仿真模拟,如图10a所示:0~1 s,电机启动并牵引加速至137.94 rad/s;1~3 s,电机转子维持在137.94 rad/s,为制动提供准备条件;3 s时进入制动工况,目标速度指令下调为0 rad/s;电机负载保持为500 N·m。跟随转子转速的动态变化,可仿真得电机输出转矩Te如图10b,中间直流环节电压Ud及整流器输入电压UN如图10c,动车组所在供电臂接触网压UT如图10d。

图10 -32‰坡度下牵引网-动车组模型仿真结果Fig.10 Simulation results of vehicle-grid model under a slope of-32‰
图10b中,当动车组进入制动工况时,可产生与原转矩方向相反的制动力矩,此时电机切换为发电机状态,符合再生制动原理。
图10c中,制动工况下,Ud受回馈电能影响发生波动,其峰值Udmax=3 130 V,在2 700 V至3 600 V的范围内,满足要求;由于脉冲整流器闭环控制采用PI调节,Ud存在一定超调,该超调量亦满足2 700 V至3 600 V的约束条件。对于CRH3型车,整流器电压额定值为1 550 V,考虑工作承载能力的冗余,通常留有1.5的裕度,故在保证机车安全的情况下UN峰值不得超过3 288 V,UNmax=2 950 V满足要求。
图10d中,受电机启动冲击与制动回馈的影响,接触网压UT抬升明显,由于在下坡时动车组出现从静止状态启动的情况较为少见,故本文仅考虑制动回馈造成的影响。制动工况下,接触网压峰值UTmax=41.60 kV,在牵引网安全供电电压峰值42.42 kV(有效值30 kV)的范围内,但超出供电电压瞬时最大峰值41.01 kV(有效值29 kV)的限值,为保证供电网络的安全性,需进一步对经过下坡度为-32‰路段的CRH3型动车组的工作时长进行讨论。
综合图10的仿真结果可知,当动车组经过下坡度为-32‰路段时,机车本身性能可满足要求,但其制动回馈电能会对供电网络的安全造成威胁。同理,对下坡度为-31‰~-28‰路段进行仿真,结果如表5所示。

表5 不同坡度下对应的Ud及UT峰值结果Tab.5 Peak results of Udand UTunder different slopes
以坡度为-32‰路段为例,此时动车组限速165 km/h,考虑到同一供电臂下接触网压处于瞬时最大值(峰值41.01 kV)的时长不得超过5 min,可检算出CRH3型动车组在一个供电臂范围内持续通过的下坡长度不得超过13.75 km。若某一供电臂存在13.75 km以上、坡度为-32‰下坡线路,需投入回收装置以保证供电网络的安全。
同理,对下坡度为-31‰,-30‰,-29‰路段进行检算,可得在动车组一个供电臂范围内可持续通过的最大坡长分别为14.33 km,14.92 km,15.58 km。
对于下坡度低于-28‰的路段,高速动车组在正常限速过程中返送的再生制动能量基本不会对牵引网供电安全造成影响。
4 基于实测数据的模型验证
实测数据取自成渝线中与李家湾变电所相连的棉丰电网,李家湾牵引变电所供电范围如图11所示。

图11 李家湾牵引所供电范围Fig.11 Lijiawan traction power supply range
各牵引变电所、分区所以及车站的位置均以成都东牵引所的位置为基准点,其中K3表示距离成都东牵引所3 km,以此类推。实测数据包括2018年3月7日李家湾牵引变电所全天有功功率测试值(测试时间间隔为5 min)以及成渝线上全天车次运行信息。为验证模型再生制动工况下仿真结果的正确性,取实测数据中采集到负有功功率值的时间段进行分析。
4.1 车次运行信息分析
2018年3月7 日16:00—16:10,车次运行位置关系见图12,李家湾牵引变电站有功功率在16:00,16:05,16:10 的实测值分别为 5.027 MW,-3.352 MW,16.758 MW。
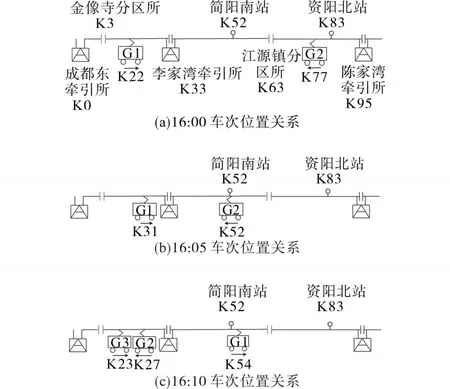
图12 16:00—16:10车次运行位置关系Fig.12 Position of EMUs from 16:00 to 16:10
16:00时G1动车组处于恒速运行工况,此时G1功率为5.027 MW;16:05时G1处于制动工况,产生的再生制动能量一部分供给同一供电臂下恒速运行的G2,剩余部分返回至李家湾牵引所,此时G1产生的再生制动功率值为-8.379 MW;16:10时G1,G2,G3均处于恒速运行工况,此时G1的有功功率为5.586 MW。
综上,考虑G1按4动4拖编组,可知G1单个变流器模块在16:00,16:05,16:10的有功功率分别为1.257 MW,-2.075 MW,1.397 MW。
4.2 仿真值与实测数据对比结果
根据4.1节中给出的有功功率推算值,结合式(11)、式(14),可计算出G1动车组模型单台电机转子转速以及负载转矩,如表6所示。

表6 G1动车组单台电机转子转速及负载转矩计算结果Tab.6 Results of calculation of rotor speed and load torque of single motor in G1 EMUs
根据表6的计算结果,在调速系统模型中设置速度目标以及负载转矩目标命令:0~2 s,电机启动并牵引加速至168.49 rad/s;2~4 s,电机转子维持在168.49 rad/s,为制动提供准备条件;4 s时进入制动工况,目标速度指令下调为0 rad/s;5~6.5 s,牵引加速,命令目标速度为187.26 rad/s;电机负载转矩保持为1 865.10 N·m。
如图13所示,动车组单个变流器模块在第一次恒速运行、再生制动运行以及第二次恒速运行消耗的有功功率分别为1.25 MW,-2.01 MW,1.40 MW,与4.1节中实测数据推算结果基本一致,可证明仿真建模及拟合函数的正确性。

图13 基二实测数据的单个变流器模块有功功率仿真结果Fig.13 The active power simulation results of a single power unit based on the measured data
4.3 与实测数据及已有文献的波形对比
图14a为李家湾牵引变电所全天24小时的功率因数实测波形(共288个测试点数),图14b为本文建立的牵引网-动车组耦合模型的功率因数仿真波形,图14c为文献[7]给出的动车组模型功率因数仿真波形。其中,文献[7]建立的模型仅考虑了复杂牵引网结构及动车组整流器,逆变器-电机系统被等效为电流源,并忽略了车顶高压电缆、车体、接地线等部件。

图14 与实测数据及已有文献的波形对比Fig.14 The waveforms compared with the measured data and literature
通过对比图14a、图14b、图14c可知,本文采用的建模方法所得的仿真结果更符合实际情况,模型的准确性更高。
5 结论
针对高速铁路中长大下坡路段动车组的再生制动能量问题,已有研究方法通常忽略牵引网、车顶高压电缆、车载变流器、车体、接地线、钢轨回路中一个或多个部件,与实际情况有一定出入,导致电路拓扑结构发生改变,从而影响模型仿真结果的准确性。鉴于此,本文考虑复杂牵引网、动车组牵引传动系统及动车组接地系统等多个部件,建立了详细的牵引网-动车组耦合模型。通过拟合制动功率与转子转速的函数关系,对模型目标指令参数进行求解,实现坡道参数与仿真模型的结合。在此基础上,结合实际数据计算分析了不同线路条件下动车组产生的再生制动能量对牵引网-动车组系统供电安全的影响,得到结论如下:
1)通过对比成渝线棉丰-李家湾的实测数据可知,本文提出的方案能精确仿真出不同线路条件下动车组产生的再生制动功率对动车组中间直流环节电压及牵引网压的抬升影响,仿真精度可达到0.01 kV,且系统功率因数的仿真结果较已有文献更为符合实际;
2)通过校核牵引网-动车组系统的供电安全性,可知对于下坡度为-32‰,-31‰,-30‰,-29‰路段,CRH3型动车组在一个供电臂范围内可持续通过的最大坡长分别为13.75 km,14.33 km,14.92 km,15.58 km;
3)对于下坡度低于-28‰的路段,CRH3型动车组在正常限速过程中返送的再生制动能量基本不会对牵引网供电安全造成影响。
综上,本文提出的方案较已有的建模方法更符合实际,且仿真结果可精确至0.01 kV。同时,本文提供的建模方法及研究结果可为复杂山区的铁路建设提供设计参考。对于其他型号动车组,可根据各车型的编组方式对变流器模块及动车组接地模型进行相应改动,其理论计算方法及仿真调控方法同理可推。
