曲梁斜拱人行桥抗震性能分析

梁并豪，贺俊峰，祝少才，邓胜杰

（1、中新广州知识城财政投资建设项目管理中心 广州 510700；2、广州大学土木工程学院 广州 510006）

0 引言

随着桥梁工程建设的快速发展，城市人行桥除了基本的功能性需求外，越来越注重桥梁美学，曲梁斜拱人行桥由于其结构线形的流畅性［1］，其在人行桥中的应用日渐增多。但曲梁斜拱人行桥的曲线空间组合构造也使结构动力特性变得更加复杂，这就对桥梁安全方面提出了许多要求，其中抗震性能是一个不可忽略的重要指标［2］。

地下结构的抗震设计分析方法常用反应谱法及相关规范建议的简化分析方法即反应位移法和反应加速度法，赵密等人［3］以深圳市某线路工程地铁站抗震分析为例，通过计算分析比较上述3种方法。分析发现反应谱法精度较高，故本文采用反应谱法进行抗震验算。

参照对单拱面预应力混凝土系杆拱桥的抗震性能分析［4］，本文以某市内曲梁斜拱人行桥为背景，在对曲梁斜拱桥结构进行E1、E2 水准地震作用下的多振型反应谱分析，在考虑纵横向地震耦合作用基础上，对上部结构各关键截面和桩基截面进行抗震验算。以此为同类桥梁的抗震分析提供参考。

1 桥梁概况

某市内曲梁斜拱人行桥主桥布置为139 m的钢拱桥，桥宽为变宽度4～6 m，拱肋理论拱轴线方程Y=−23.2X2/292，计算跨径58.0 m，矢高23.2 m，计算矢跨比为1/2.5，拱肋整体外倾20°。

钢主梁断面为单箱单室断面，拱肋截面为正五边形。桥梁采用可更换性吊杆索具，全桥共设置13根吊索。吊索沿主拱肋及主跨均为对称布置。桥型布置如图1所示，侧视图如图2所示。

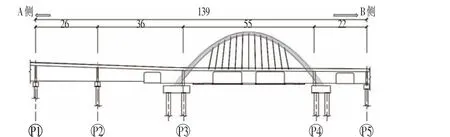
图1 桥型布置Fig.1 Bridge Layout Plan （m）

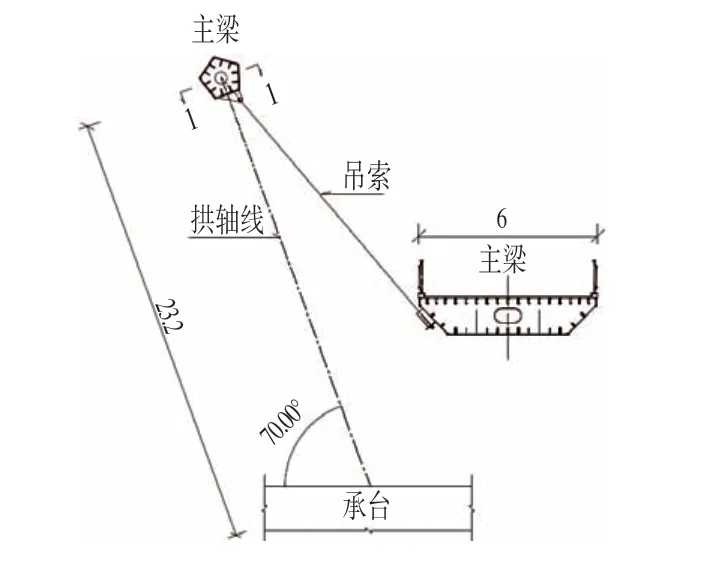
图2 桥梁侧视图Fig.2 Bridge Side View （m）

2 地震动输入

参照《城市桥梁抗震设计规范：CJJ 166—2011》［5］和《公路桥梁抗震设计规范：JTG/T 2231−01—2020》［6］，本桥主桥设计地震作用采用场地50 年超越概率10%地震动，罕遇地震作用采用场地50 年超越概率2%地震动。

根据提供的地震动参数，本桥场地地震动峰值加速度为0.1g，反应谱特征周期为0.45 s。50 年10%（设计地震作用E1）和50 年2%（罕遇地震作用E2）超越概率的加速度反应谱（阻尼比5%）计算公式见式⑴。竖向地震作用均取相应水平地震动的0.65倍。

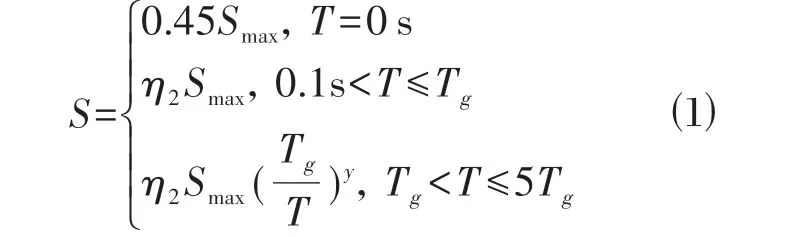
上述各参数的取值如表1所示。

表1 工程场地地表水平向设计地震动加速度反应谱（2%阻尼比）参数值Tab.1 Parameter Value of the Horizontal Design of Ground Motion Acceleration Response Spectrum（2%Damping Ratio）on the Surface of the Engineering Site

在E1、E2地震作用下的加速度反应谱如图3所示。

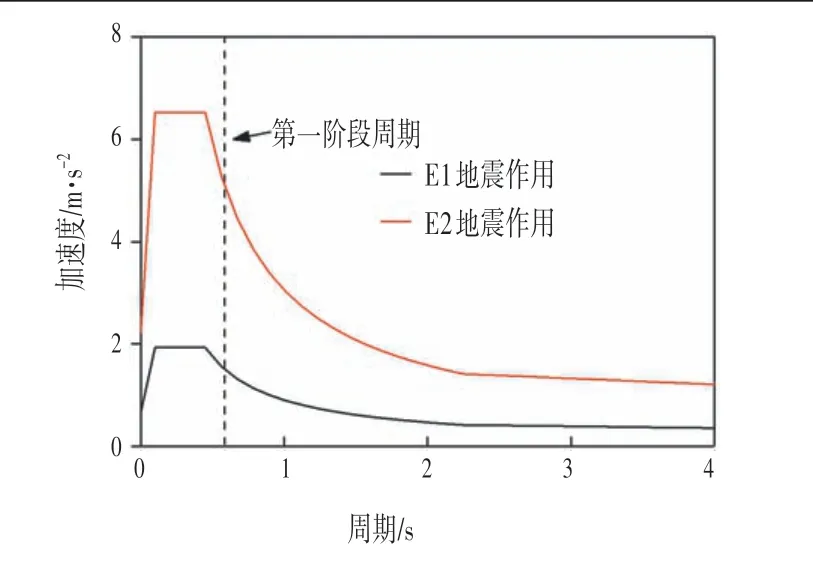
图3 加速度反应谱Fig.3 Acceleration Response Spectrum

3 有限元分析模型与动力特性

3.1 有限元分析模型

文章采用Midas Civil 对桥梁进行建模分析，主梁与拱肋采用梁单元模拟，吊杆采用桁架单元模拟，所有桥墩采用墩梁固结刚性连接，临时墩与主梁之间采用弹性支座连接，承台与桩基采用主从节点刚性连接［7］。桥梁整体有限元模型如图4所示。

图4 桥梁有限元模型Fig.4 Finite Element Model of Bridge

3.2 结构动力特性分析

根据所建立的有限元分析模型，对本桥进行结构动力特性分析，得到桥梁的前10 阶自振频率和振型（见表2），并给出了前2阶振型图（见图5）和横桥向及竖向桥梁各阶振型的质量参数系数分布图（见图6），可发现图6中高阶振型的贡献比较显著。

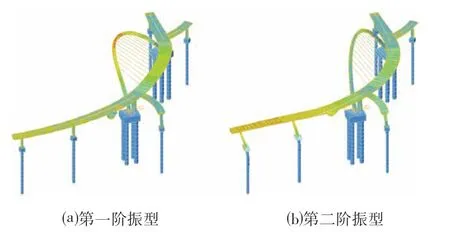
图5 桥梁振型Fig.5 Vibration Mode of Bridge Girder

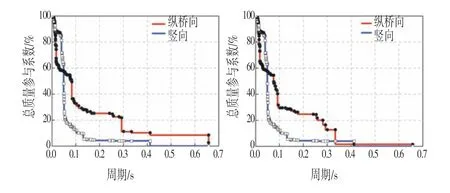
图6 各阶振型质量参数系数分布Fig.6 Distribution of Mass Parameter Coefficients of All Modes

表2 桥梁前10阶自振频率和振型Tab.2 First 10 Natural Vibration Frequencies and Modes of the Bridge

4 主桥反应谱分析结果与验算

在主桥动力特性分析所采用的有限元模型中，按照两阶段设防，分别输入E1 和E2 两种概率水准地震作用下的结构响应，对结构进行反应谱分析。为了考虑大桥不同方向振动的耦合效应，地震输入分别采用纵桥向和横桥向［8］。在验算时，综合考虑纵向地震输入和横向地震输入结构地震反应。因为在地震作用下没有非线性构件，所以采用反应谱分析方法可反映结构的地震反应。下面给出地震作用下反应谱分析计算结果及其性能校核结果。

4.1 拱肋

人行桥的拱肋和主梁等构件采用钢结构，根据《公路钢结构桥梁设计规范：JTG D64—2015》［9］，计算拱肋和主梁各关键截面的面积和抗弯抵抗矩，计算在多重内力作用下钢材的最大应力，将之与钢材的允许强度进行比较，判断钢材是否进入塑性状态，如式⑵：

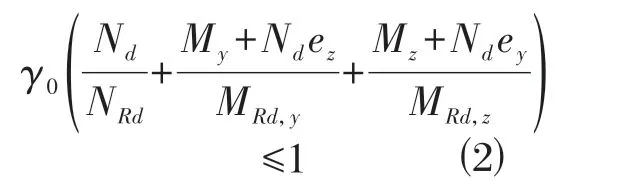
得出截面的抗弯能力与所受弯矩最不利值进行比较验算，主要结果如表3～表4 所示。根据表格数据可知，拱肋在E1、E2 地震作用下，各关键截面的弯矩最不利值均小于抗弯能力，所有截面均处于弹性工作状态，抗弯能力验算通过。

表3 E1地震作用下上部结构各关键截面抗震验算结果Tab.3 Seismic Checking Results of Each Key Section of the Superstructure under E1 Earthquake （kN·m）

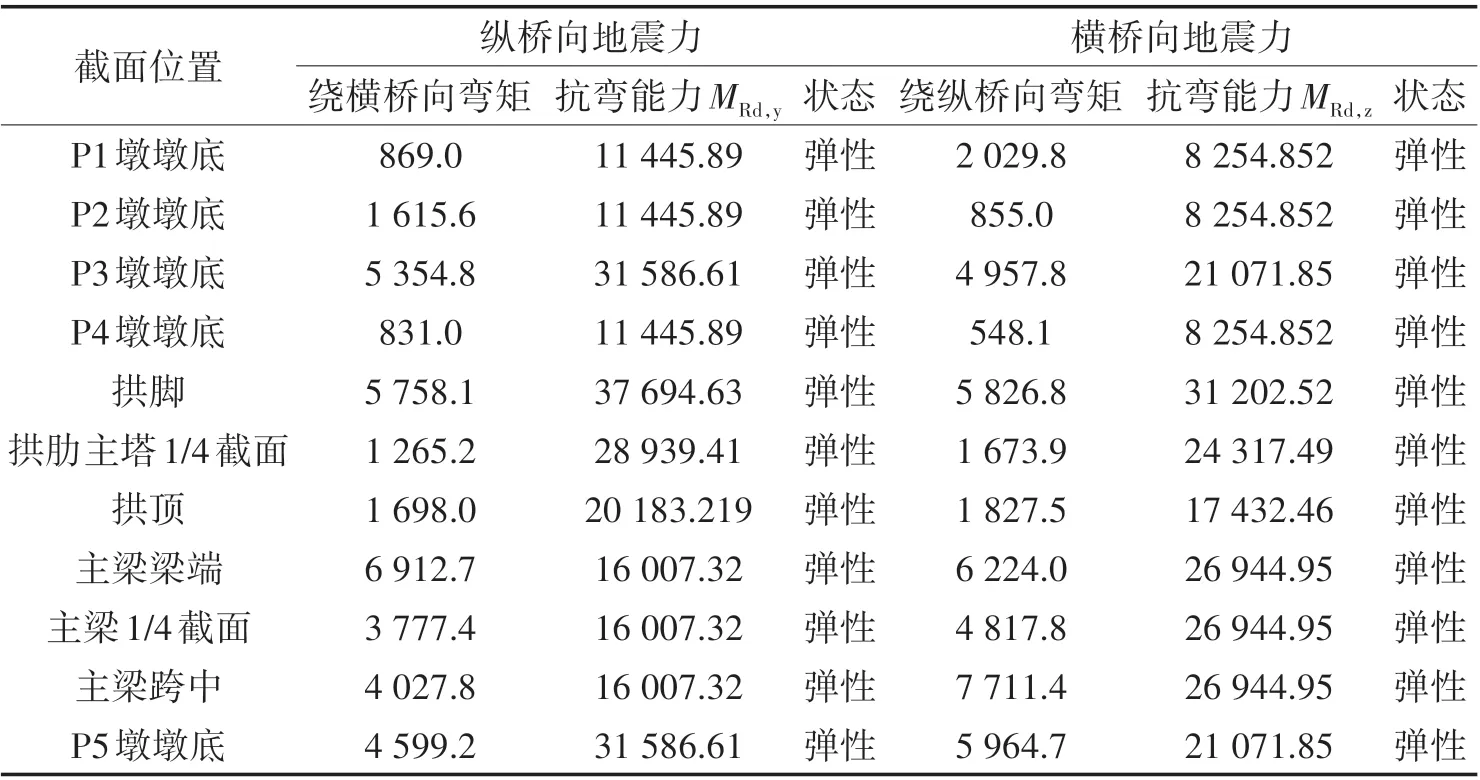
表4 E2地震作用下上部结构各关键截面抗震验算结果Tab.4 Seismic Checking Results of Each Key Section of the Superstructure under E2 Earthquake （kN·m）

4.2 桩基础

墩柱和桩基关键截面为钢筋混凝土截面，在模型分析中常将其划分为纤维单元模型［10］，具体验算方法及过程如下：将墩柱和桩基截面划分为纤维单元，在划分纤维单元时，混凝土和钢筋单元分别划分，钢筋和混凝土单元分别采用实际的钢筋和混凝土应力−应变关系。利用实际的钢筋和混凝土应力−应变关系，采用截面数值积分法进行弯矩−曲率分析（考虑响应轴力），得到图7 所示弯矩−曲率曲线，其中1.2 m 桩基对应图1 中的P2、P5，1.8 m 桩基对应图1中的P3、P4。

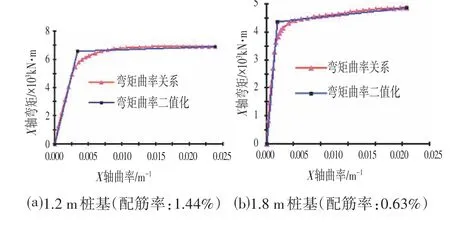
图7 桩基截面弯矩-曲率曲线示意图Fig.7 Schematic Diagram of Bending Moment-curva⁃ture Curve of Pile Foundation Section

在设计地震作用下，墩柱和桩基截面要求其在地震作用下的截面弯矩应小于截面初始屈服弯矩（考虑轴力）My。由于My为截面最外层钢筋首次屈服时对应的初始屈服弯矩，当地震反应弯矩小于初始屈服弯矩时，整个截面保持在弹性，结构基本无损伤，满足设计地震水平下的性能目标。

罕遇地震作用下，墩柱和桩基截面要求其在地震作用下的截面弯矩应小于截面等效抗弯屈服弯矩Meq（考虑轴力）。从理想弹塑性双线性模型看，当地震反应小于等效抗弯屈服弯矩Meq，结构整体反应还在弹性范围。

然而，区别于常规结构形式的桥梁，曲梁斜拱人行桥的空间复杂性要求My和Meq考虑多向地震输入耦合情况的影响。因此，为了考虑基于多向地震输入考虑不同输入方向对桥梁效应的影响，本文结合文献［4］中的有关规定，在采用反应谱法时考虑横纵方向耦合效应，提出的最不利效应弯矩效应的计算方法如式⑶所示：

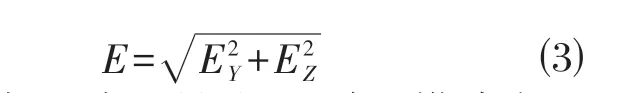
主要结果如表5～表6 所示。可知，拱肋在E1、E2地震作用下，各关键截面的弯矩最不利值均小于抗弯能力，能力需求比满足要求，所有截面均处于弹性工作状态，抗弯能力验算通过。但通过能力需求比可以看出，部分桩基地震反应较大。

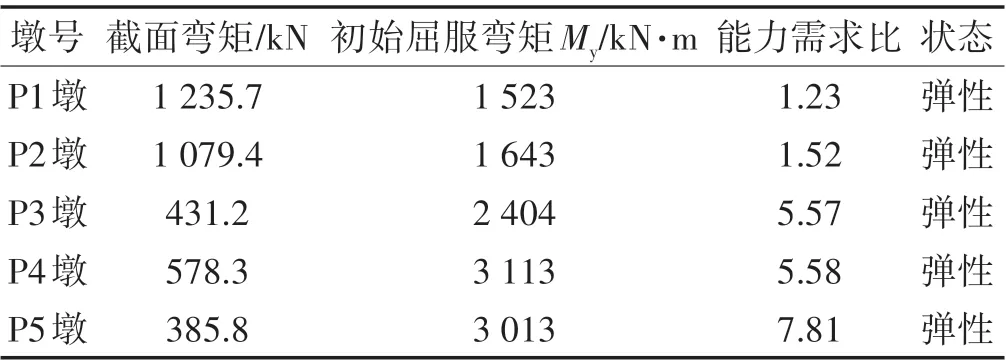
表5 E1地震作用下桩基截面抗震验算结果Tab.5 Seismic Checking Result of Pile Foundation Section under E1 Earthquake

表6 E2地震作用下桩基截面抗震验算结果Tab.6 Seismic Checking Result of Pile Foundation Section under E2 Earthquake

5 结论

采用Midas Civil 有限元软件建立某曲梁斜拱人行桥的动力分析模型，并对结构进行E1、E2 水准地震作用下的反应谱分析，对上部结构各关键截面和桩基截面进行抗震验算，可得出如下结论：

通过对结构进行E1、E2 水准地震作用下的反应谱分析，对上部结构各关键截面和桩基截面进行抗震验算，结果表明E1、E2 水准地震作用下，人行桥所有拱肋、主梁、墩柱截面及桩基础均能满足预期性能目标要求。

在E1、E2 水准地震作用下，人行桥所有拱肋、主梁、墩柱截面及桩基础最不利单桩截面地震弯矩小于其对应的初始屈服弯矩，截面保持为弹性工作状态，满足预期性能目标要求，且根据抗震分析结果，人行桥主体结构地震反应较小，而桩基地震反应较大，因此在同类桥梁的抗震分析中应更加注重桩基性能。