人行桥竖向人致振动响应参数及其敏感性分析

2021-04-07陈丹丹孟丽岩

黑龙江科技大学学报 2021年2期

王涛，陈丹丹，孟丽岩，郑欢

(黑龙江科技大学建筑工程学院，哈尔滨 150022)

0 引言

近十多年来，人致桥梁振动分析一直是学者们关注的热点问题。在设计新结构尤其是人行天桥时，考虑到人致振动的舒适性和安全性，人致振动变得越来越重要。当代人行天桥设计的挑战在于满足对长、轻、细结构的建筑需求。基于现行标准，很多新建人行天桥在使用时容易产生过大振动，可能会令行人感到不舒适。最典型的例子是1999年巴黎索尔费里诺桥[1]和2000年伦敦千禧桥[2]均在启用时因行人活动导致的过度振动而关闭。近年来，国内外众多学者在人致振动领域已经进行了许多研究。Caprani等[3]考虑了竖向振动的人-结构相互作用系统模型，给出了不同行人荷载模型作用下模态分析和有限元分析公式，对比分析不同行人荷载模型对简支梁结构动力特性的影响。汪志昊等[4]通过试验研究了静立、静坐和下蹲3种姿态下人行桥竖向基频和阻尼比的变化情况。陈得意[5]推导出人致桥梁振动响应解析解，并在此基础上进行了不同参数对人行桥人致振动舒适度影响的探究。操礼林等[6]比较分析了不同人体质量、人体刚度及人体阻尼比对人行桥瞬时频率、瞬时阻尼比和人行桥振动响应的影响。目前，基于有限元分析理论从行人参数及人行桥参数两个方面对人致振动响应分析的研究成果相对较少。

笔者基于有限元理论给出了人行桥人致振动有限元分析方法，采用Matlab编程求解人-桥竖向相互作用动力控制方程，分析了人致桥梁振动动力响应，结合算例进行了不同行人参数以及人行桥参数对人行桥人致振动响应规律的探究，并在不同参数分析的基础上进行了参数敏感性分析。

1 人行荷载模型

1.1 移动力模型

在进行人致振动分析时，通过将行人简化成一个移动力(Moving force，MF)，图1为行人的移动力简化模型和桥梁的有限元模型。

在此模型中，行人移动力的大小可以用傅里叶级数模型[7-9]来表示，即

(1)

式中：Fpv(t)——竖向步行荷载激励荷载，N；

W——人的体重，N；

n1——模型中主谐波考虑的阶数；

n2——模型中次谐波考虑的阶数；

αvi——竖向第i阶主谐波动载因子；

αvsi——竖向第i阶次谐波动载因子；

fp——人的步频，Hz；

φvi——竖向第i阶主谐波相位角，rad；

φvsi——竖向第i阶次谐波相位角，rad。

图1 行人的移动力模型

由于中国居民身体特征参数与外国居民存在一定差别，文中所采用的主次谐波傅里叶级数模型参数选取陈隽[10]所建议的参数取值。

1.2 移动弹簧质量阻尼模型

图2为人体的弹簧质量阻尼(Spring-mass-damper，SMD)简化模型和桥梁的有限元模型，在此模型中，人体被建模为具有刚度kp、阻尼cp、质量mp的单自由度系统。

图2 行人的SMD模型

2 人致振动有限元分析

采用有限元表示桥梁结构，建立人体-结构系统的移动力模型和移动弹簧-质量-阻尼器模型。在桥梁的有限元描述中，将桥梁离散成ne个单元，位移场采用具有三次Hermitian插值形函数的二维刚架单元近似，每个节点有3个自由度。假设行人在整个过桥的过程中始终与桥梁表面紧密接触。

动力平衡方程的有限元基本公式为

(2)

式中：M——结构的质量矩阵；

C——结构的阻尼矩阵；

K——结构的刚度矩阵；

d——节点的位移向量；

P——节点的荷载向量。

移动力分析如图3所示，动力平衡方程的自由度仅为桥梁的自由度，节点的荷载向量P为

P=NT(x)Fpv(t)，

(3)

式中，N(x)——形函数行向量。

图3 行人的MF模型和梁的FE模型

移动力以恒速v移动，随着时间迁移作用在桥梁的不同单元上，第j个单元形函数行向量由下式给出，即

(4)

式中：z——行人的位置与行人所在梁单元起点的位移；

le——梁单元长度；

x——行人距梁左端的位移；

xj——梁单元第j个节点距梁左端的位移；

γ——沿梁单元无量纲的距离，γ∈[0,1]。

形函数对x的一阶导数和二阶导数为

(5)

形函数共有2(ne+1)列，表达式为

N(x)={01×6…Nj(x) … 01×6}。

(6)

移动弹簧-质量-阻尼模型分析如图4所示。

图4 行人的SMD模型和梁的有限元模型

行人移动弹簧-质量-阻尼模型的运动方程由下式给出，即

(7)

式中：y——行人相对平衡位置的竖向动位移；

w——桥梁的竖向动位移；

式中：Vi为城市扩展速度；ΔUij为j时段第i个研究单元城市扩展面积，Δtj为j时段的时间跨度(一般以年为单位)。

SMD和桥梁之间的相互作用力由下式给出，即

(8)

桥梁的位移函数w(x,t)用形函数向量来表示，即

w(x,t)=N(x)d(t)。

(9)

式(9)中位移函数对空间微分，即

(10)

式(9)中位移函数对时间微分，即

(11)

(12)

将式(12)代入式(7)可以得到

(13)

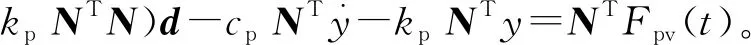
(14)

类似地，行人SMD的运动方程可以表示为

(15)

联立式(14)、(15)，人-桥相互作用运动方程为

(16)

当SMD不在桥上时，形函数向量全部为0，上述方程就变成桥梁的自由振动。

3 人致振动响应参数及其敏感性

根据上述人行桥有限元分析方法理论，将人桥耦合系统分为行人、桥梁两个子系统，然后分别建立动力平衡方程，并由行人、桥梁两者之间的位移及力的协调关系把行人和桥梁耦合在一起。在Matlab中建立桥梁的FE模型，根据行人、桥梁两者之间的位移和力的协调关系，采用状态空间法求解出行人和桥梁的动力响应，分析行人不同质量、步频及人行桥不同单位长度质量、刚度、阻尼比等参数下的人行桥人致振动响应变化规律，并分析参数敏感性。人-桥相互作用整体分析流程如图5所示。

算例分析：人行桥跨度为50 m，截面尺寸为b×h=2.000 m×0.535 m，人行桥单位长度质量M为500 kg/m，抗弯刚度B为5.1 GN·m2，阻尼比ζ为0.005。人体质量mp取中国男性质量均值66.2 kg[11]，行人步频fp为2.0 Hz，根据Silva[12]非线性表达式取人体刚度kp为12.37 kN/m，人体阻尼cp为758.63 N·s/m。

图5 人-桥相互作用分析流程

3.1 人行桥人致振动响应参数分析

从行人及人行桥两个方面分别探究对人致振动响应的影响，选取不同的行人参数和不同的人行桥参数人行桥进行人致振动响应分析。人行桥人致振动舒适度评估指标主要包括峰值加速度、均方根加速度和振动剂量，均方根加速度的定义为

(17)

式中：a——均方根加速度，m/s2；

T——振动持续时间，s；

aw(t)——加速度时程。

文中主要采用振动持续时间为1 s的均方根加速度，即1 s均方根加速度a1。

分别采用MF和SMD两种行人荷载模型，求解行人不同质量、步频及人行桥单位长度质量、刚度、阻尼比下的人行桥跨中1 s的均方根加速度响应a1。两种模型下人行桥跨中a1随各参数变化分别如图6、7所示。

图6 MF模型作用下a1随各参数变化

图7 SMD模型作用下a1随各参数变化

由图6可知，人行桥跨中a1随mp的增大而增大。当mp为50 kg时，人行桥跨中a1最大值为0.663 m/s2；当mp为80 kg时，人行桥跨中a1最大值为1.060 m/s2。人行桥跨中a1随fp的增大先增大后减小。当fp为1.4 Hz时，人行桥跨中a1最大值为0.019 m/s2；当fp为2.0 Hz时，人行桥跨中a1最大值为0.877 m/s2；当fp为2.6 Hz时，人行桥跨中a1最大值为0.050 m/s2。这主要是因为随着fp的逐渐增大，fp与人行桥基频渐渐接近，人行桥跨中a1随之增大；fp持续增大，fp逐渐远离人行桥基频，人行桥跨中a1随之减小。人行桥跨中a1随M的增大先增大后减小。当M为200 kg/m时，人行桥跨中a1最大值为0.035 m/s2；当M为500 kg/m时，人行桥跨中a1最大值为0.877 m/s2；当M为800 kg/m时，人行桥跨中a1最大值为0.047 m/s2。这主要是因为人行桥M的增大导致人行桥基频改变，随着M增加，桥梁基频逐渐增大，当桥梁频率与fp一致时发生共振，跨中a1达到最大值；M持续增大，fp渐渐远离桥梁基频，跨中a1逐渐减小。人行桥跨中a1随B的增大先增大后减小。当B为3.6 GN·m2时，人行桥跨中a1最大值为0.047 m/s2；当B为5.1 GN·2时，人行桥跨中a1最大值为0.877 m/s2；当B为6.6 GN·m2时，人行桥跨中a1最大值为0.046 m/s2。这主要是因为B的增大会使人行桥固有频率随之变化，随着B增加，桥梁固有频率逐渐增大，当桥梁固有频率与fp一致时发生共振，跨中a1达到最大值；B持续增大，fp渐渐远离桥梁固有频率，跨中a1逐渐减小。人行桥跨中a1随的增大先增大后减小。当ζ为0.005时，人行桥跨中a1最大值为0.877 m/s2；当ζ为0.011时，人行桥跨中a1最大值为0.360 m/s2。

由图7可知，SMD模型作用下，人行桥跨中a1随各参数变化趋势与MF模型作用下一致。

MF模型和SMD模型作用下人行桥跨中1 s均方根加速度响应随各参数变化对比如图8所示。

由图8可知，当mp为80 kg时，两种模型作用下人行桥跨中a1最大值a1 max相差0.285 m/s2；当fp为2 Hz时，两种模型作用下人行桥跨中a1 max相差0.161 m/s2；当M为500 kg/m时，两种模型作用下人行桥跨中a1 max相差0.161 m/s2；当B为5.1 GN·m2时，两种模型作用下人行桥跨中a1 max相差0.161 m/s2；当ζ为0.005时，两种模型作用下人行桥跨中a1 max相差0.161 m/s2。

图8 不同模型下a1最大值对比

综上所述，MF和SMD两种行人荷载模型下人行桥跨中a1相差较大，MF模型未能考虑人-桥相互作用，放大了人行桥响应。

3.2 人行桥人致振动响应参数敏感性分析

在上述不同行人参数及人行桥参数分析基础上，进行人行桥人致振动参数敏感性分析。参数敏感性分析是为了选出对人行桥响应影响最大的参数，以便更好地评估人行桥振动响应。一般通过计算敏感度系数来进行敏感性分析：

(18)

式中：SAF——敏感度系数；

ΔA/A——各评价指标变动时的比率；

ΔP/P——各不确定参数发生变动时的比率。

由前文参数分析可知，随着人体质量的增大，人行桥跨中a1响应随之增大，随着人行桥阻尼比的增大，人行桥跨中a1响应随之减小，随着行人质量、人行桥单位长度质量及人行桥刚度的增大，人行桥跨中a1响应随之呈现先增大后减小的趋势。表1对比了两种不同行人荷载模型作用下a1响应对各参数的敏感度系数。

表1 MF和SMD模型敏感度系数对比

由表1可知，对于MF模型而言，人行桥跨中a1响应对行人质量的敏感度系数为1.00，人行桥跨中a1响应对人行桥阻尼比的敏感度系数为-1.40，人行桥跨中a1响应相比行人步频等其他参数对行人质量和人行桥阻尼比更加敏感；对于SMD模型而言，人行桥跨中a1响应对人行桥刚度的敏感度系数为0.67，人行桥跨中a1响应对人行桥阻尼比的敏感度系数为-1.38，人行桥跨中a1响应对人行桥阻尼比和刚度更为敏感。综上所述，无论是MF模型还是SMD模型，人行桥响应均对人行桥阻尼比参数最为敏感。为满足人致工程振动舒适度要求，通过增加阻尼比的方式进行人行桥减振控制效果更为理想。