基于荷载—结构法的明挖隧道结构有限元模拟方法
2022-09-07彭聪
彭 聪
(广州市市政工程设计研究总院有限公司 广州 510060)
0 引言
对于隧道地下结构设计计算,一般有经验设计法、实用设计法、作用与反作用模型(荷载—结构法)、连续介质法4 种方法[1]。对于明挖隧道结构而言,在工程设计中与一般地面结构受力方式较为相近,多采用荷载—结构模型进行计算[2]。随着科学技术的发展,有限元数值计算软件开始进入到结构设计领域,目前ADINA、ABAQUS、SAP、ANSYS、MIDAS 等系列软件在隧道结构设计中已得到普遍应用[1],工程设计人员利用有限元软件完成了大量的隧道结构验算和研究工作[3−6],但这些计算软件的发展和应用仍脱离不了对基础理论的依赖,国内罗衍俭等学者[7−11]均在隧道结构数值模拟的基础工作中做出了大量贡献。而在工程设计领域鲜有人从理论角度出发对结构进行剖析,往往通过有限元数值结果结合以往工程经验来完成结构设计验算。为满足工程设计人员需要,本文从隧道荷载−结构模型基础理论出发,通过拆解分析,提出基于Midas Civil 的隧道结构数值模拟计算方法,并提出在特定工况下应将弹性地基梁法作为有限元计算的补充。
1 隧道结构受力分析
对于隧道结构,所受外荷载一般有自重、侧土压力、水压、顶板覆土压力、隧道内活载、隧道内恒载,其荷载−结构模型受力简图如图1 所示,隧道底板边界按弹性地基梁考虑,计q1为侧土压力,q2为底板水压,q3为顶部覆土压力(含顶板自重),q4为隧道内荷载(含底板自重)。
由于隧道底板边界为仅受压边界(非线性边界),这意味着问题的求解不再是简单的线性问题,不难理解,若在某个特定工况下,仅受压边界局部区域不参与结构受力,此时结构存在内力重分布的现象,其求解往往需要进行多次迭代计算,这即说明仅受压边界仅在全部边界都参与结构受力时,结构才能满足线性计算理论,本文所有的分析均建立在仅受压边界全部参与结构受力的基础上。
对于图1的荷载,由于结构荷载对称,结构在仅受q1荷载作用下自由变形,仅受压边界不参与受力,因此可将结构拆分为图示工况①和工况②的叠加,如图2所示。
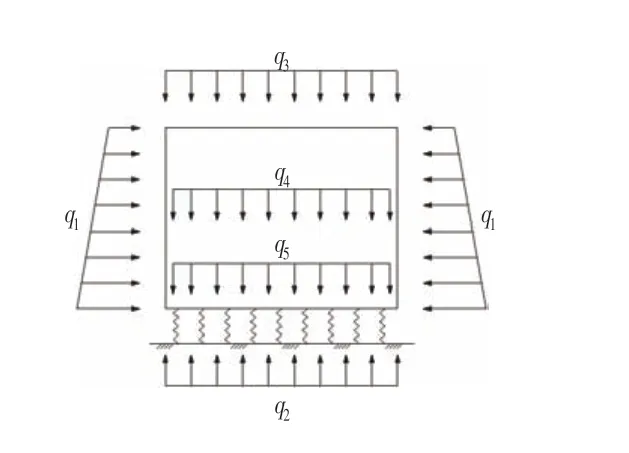
图1 隧道结构荷载-结构模型Fig.1 Tunnel Structural Load-Structure Model
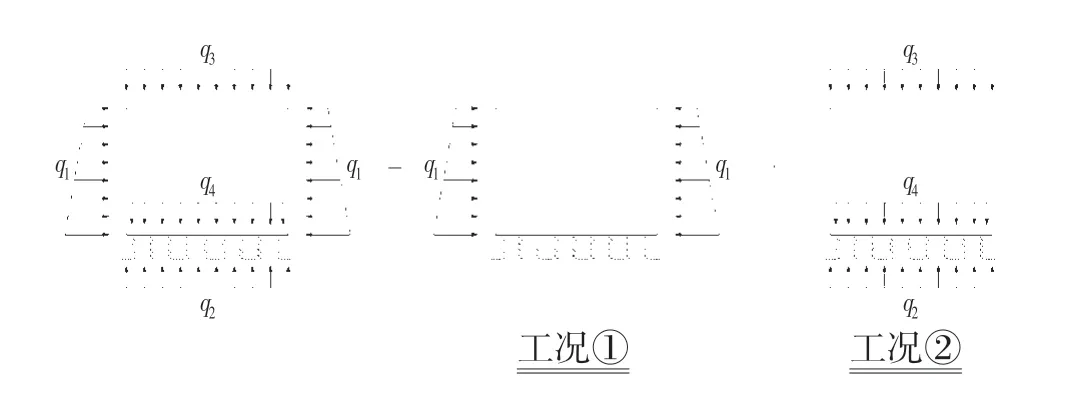
图2 荷载拆解分析Fig.2 Load Dismantling Analysis
工况①可利用结构力学知识快速进行求解,本文不再赘述。而对于工况②,一般有q2≤q3+q4,弹簧参与结构受力,考虑一般情形,隧道底板紧贴于地基,不存在脱空,此时隧道结构满足线性计算条件,但对于工况②带来的结构响应,仍然需要分情况加以讨论。
1.1 工况②−1:q2−q4≤q3(q4≤q2)
该工况一般对应于埋深较深或处于高水位工况的隧道结构。此时,隧道结构的受力简图如图3所示,根据结构荷载对称,亦可简化成图3 中工况①的结构荷载形式,并将侧墙自重简化成竖向集中力作用于顶板角点处。仅考虑一般情形,隧道底板与地面始终保持紧密接触,仅受压边界全程参与结构受力,因此原结构可简化成图3 中工况②的受力形式,显然,求解q(x)十分困难,其与结构自身刚度、外部荷载大小、边界条件均有关系,这里,为简化问题,考虑到隧道底板仅受压边界的整体连续性和刚度的一致性,取q(x)=F/l+q3−(q2−q4)(l为结构宽度,下同),至此可以通过平衡方程快速求解结构内力,本文不再赘述。
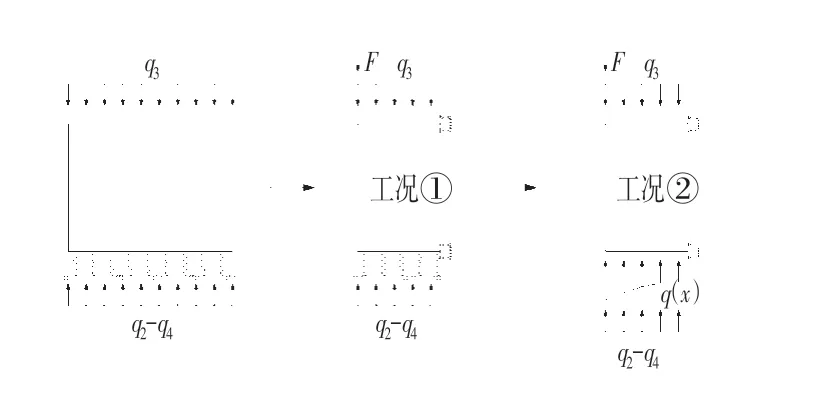
图3 工况②-1简化图示Fig.3 Simplified Diagram of Working Condition ②-1
1.2 工况②−2:q4−q2≤q3(q2≤q4)
该工况一般对应于埋深较浅或处于低水位工况的隧道结构。此时,隧道结构的受力简图如图4⒜所示,根据结构荷载对称,简化成图4⒝的结构荷载形式,并将侧墙自重简化成竖向集中力作用于顶板角点处。仅考虑一般情形,隧道底板与地面始终保持紧密接触,仅受压边界全程参与结构受力,此时仍然可以将图4⒝所示荷载拆解成图4⒝中工况①和工况②的叠加形式,对于图中工况①,仍可按2.1节中的方法进行分析,且不难得出,其受力与2.1节中的工况②−1一致。然而,在图4⒝中工况②的作用下,结构将仅发生刚体位移,结构并无内力产生,但在隧道实际运行中,由于侧墙的存在,其与土层之间的摩擦力将限制隧道结构产生刚体位移,且侧墙对底板也具备相当的约束,此时,隧道底板必然产生结构内力,且对于某种特殊情况:q4−q2>F/l+q3,结构底板将出现底边缘受拉的情况,若再采用图4⒝中的工况②模型进行计算对结构验算将不满足保守原则。因此,不论是上述拆分的理论模型还是基于此的荷载−结构有限元模型均变得不可靠。

图4 工况②-2简化图示Fig.4 Work Condition ②-2 Simplified Diagram
为解决上述问题,将隧道底板独立出来,简化成两端固结的弹性地基梁模型(见图5),以弹性地基梁来计算隧道底板受力。
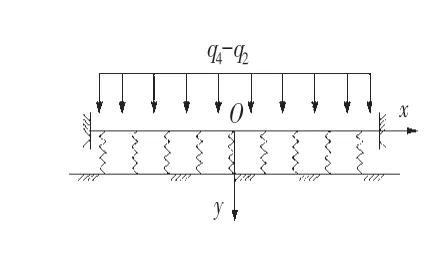
图5 底板地基梁模型Fig.5 Base Plate Foundation Beam Model

根据初始参量法,通过以上边界条件即可求得地基梁各个位置的内力,本文不再赘述。
2 基于Midas Civil分析隧道结构
通过上一小节对隧道结构荷载的拆解分析可知,隧道结构的受力与荷载形式、边界条件有着密不可分的关系,利用有限元计算软件建立荷载−结构模型模拟隧道结构受力时,若采用仅受压边界作为边界条件,此时将引出两个问题:①由于仅受压边界无法抵抗结构向上运动的趋势,因此地下水荷载不能作为单独的计算工况,否则模型将产生刚体位移导致计算结果不收敛;②在利用有限元计算隧道结构时,常采用节点仅受压弹簧(即在单元节点处设置点弹簧),由于节点弹簧并非连续边界,弹簧刚度在基床系数取定的情况下跟单元长度、计算节段宽度存在一定比例关系,这即意味着弹簧刚度的取值具备较大的弹性(原则上单元长度越小越精确)。
2.1 针对问题①
⑴方法一:Midas Civil程序的“施工阶段”功能可实现荷载的逐级累加,应用此功能即可消除单独地下水荷载作用下模型计算出现刚体位移而出现的结果不收敛问题,Midas Civil在提供逐级累加功能时,还可以将施工阶段累加的荷载通过“施工阶段”功能单独提取出来,至此即可对单独提取的工况进行组合。
⑵方法二:定义两种中间工况:G1=q2+q3+q4(全部竖向荷载之和)、G2=q3+q4(全部重力方向荷载),在荷载组合中定义组合G=G1−G2,此时G即为单独地下水荷载作用下结构的响应工况,至此即可对不同工况进行组合完成结构验算
2.2 针对问题②
Midas Civil程序“面弹性支承”中的分布弹性支承仅受压杆系边界,通过定义杆系梁宽度和基床系数即可用来模拟连续弹性边界,这即消除了节点仅受压弹簧刚度取值弹性大的问题,但这种边界缺点在于不能用于施工阶段分析。
结合以上分析和Midas Civil 计算软件的特点,提出两种基于Midas Civil的有限元建模方式:
⑴建立施工阶段模型,并在施工阶段中激活全部荷载,将荷载在施工阶段中单独剥离,计算完成后,对各提取出来的工况进行组合完成结构验算。
⑵ 采用分布弹性支承仅受压杆系边界,按问题①定义中间工况的方式进行结构验算。
3 算例分析
3.1 工程概况
广州某过江隧道南岸岸上段主线起点里程K0+080,终点K0+725,全长645 m(其中敞开段372 m,暗埋段273 m),双向四~八车道,设有A~F 共6 条匝道,匝道总长1 899.238 m(其中敞开段467 m,暗埋段1 432.238 m),单向一~二车道。隧道整体布置如图6所示。
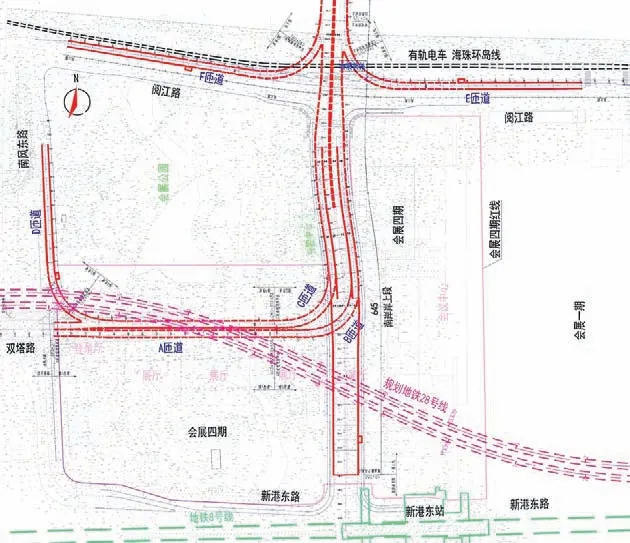
图6 过江隧道南岸岸上段平面布置Fig.6 Plan of the South Shore Section of the Exhibition West Crossing
以A 匝道标准节段作为本文算例,隧道结构构造如图7所示,隧道主体结构采用C40混凝土,弹性模量为3.25×107kN/m2,计算模型取隧道纵向宽度1 m,基床系数取15 000 kN/m3。分高低两种工况计算,隧道两侧均为杂填土,隧道水土压力采用水土合算,结构外荷载如表1所示,结构自重程序自动计算。
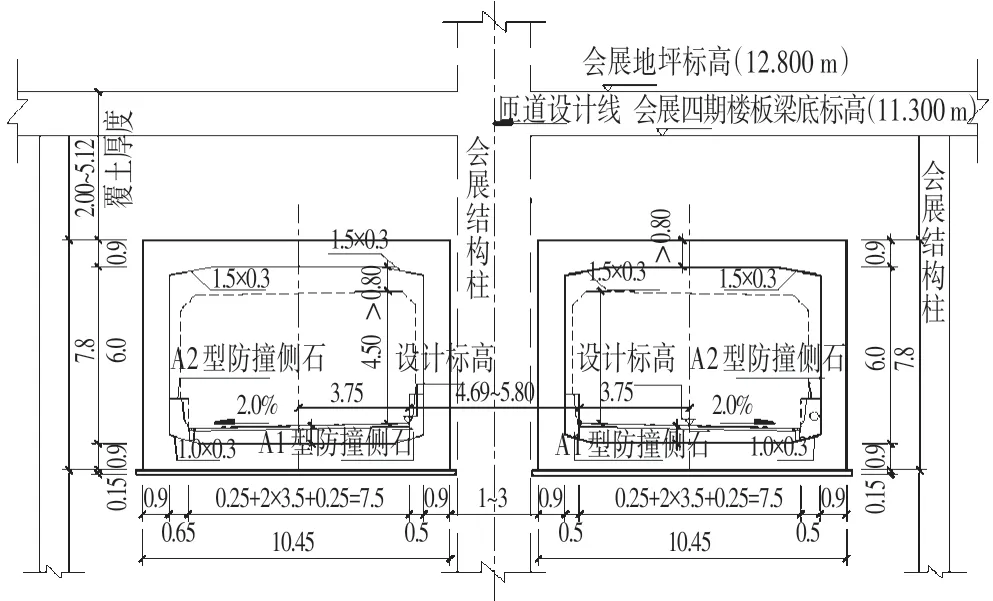
图7 A匝道隧道标准节段构造Fig.7 A Ramp Tunnel Standard Section Construction(m)
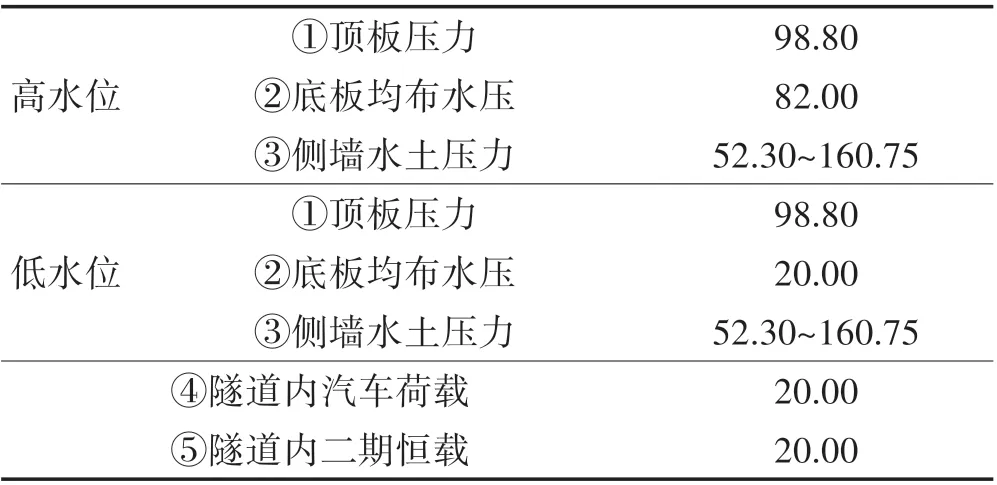
表1 隧道荷载一览Tab.1 List of Tunnel Loads (kN/m2)
3.2 计算结果分析
选取A~E 五处关键位置进行计算分析,如图8 所示。有限元模型单元类型均为梁单元,模型共计72个节点,72 个单元,底板单元长度0.25 m,采用节点仅受压弹簧模拟时,刚度为0.25(单元长度)×1(计算宽度)×15 000(基床系数)=3 750 kN/m,有限元计算模型如图9 所示,计算结果如图10 所示,图10 中工况1:高水位①+②+④+⑤+自重;工况2:低水位①+②+④+⑤+自重;工况三:③,直柱图上部为各方法与理论值的误差(|有限元值−理论值|/理论值×100)。在计算低水位工况时,利用弹性地基梁法分别求得隧道底板跨中和两端弯矩为65.5 kN·m和520.1 kN·m。
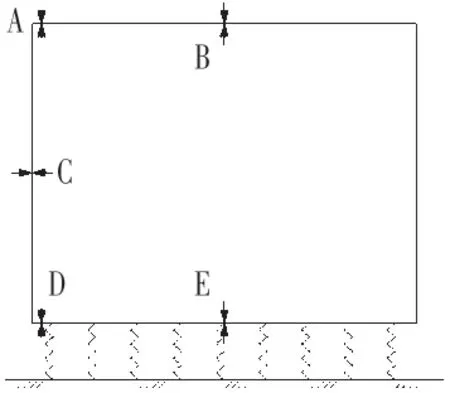
图8 关键截面图示Fig.8 Illustration of Key Sections

图9 有限元模型Fig.9 Finite Element Model
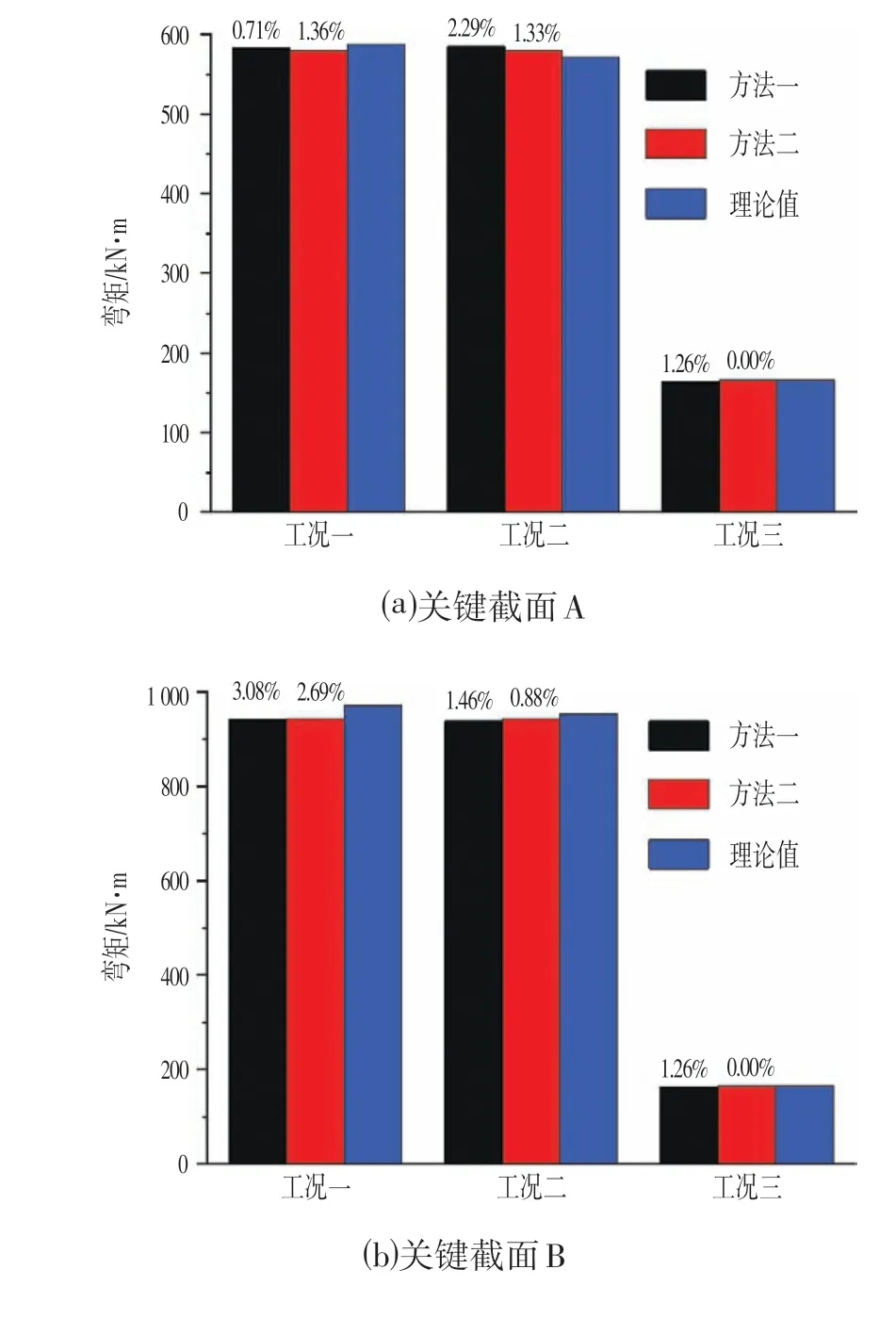

图10 关键截面弯矩对比直柱图Fig.10 Key Section Bending Moment Comparison Histogram
4 结论
本文通过将隧道结构外荷载进行拆解,对隧道结构受力情况进行了理论分析,并在此基础上提出两种基于Midas Civil的有限元建模方法,得到如下结论:
⑴通过理论分析可知,有限元模型和理论模型无法准确计算特定工况下真实的结构响应,此时可将底板按弹性地基梁进行受力分析。
⑵通过算例分析,两种有限元建模方法均具备较高的精度,特别是有限元建模方法二由于弹性边界连续精度更高,其中方法一建模过程繁复,中间过程较为费时,但建模思路清晰,易于工程人员接受,方法二建模简单,无需设置施工阶段,但对基础理论要求较高。
⑶对于隧道底板底边缘受压的情况,采用上述两种计算方法均能满足设计要求,但对于隧道底板底边缘受拉的情况,在结构验算时,有必要考虑采用弹性地基梁计算得到的结构响应。
