轮对空心轴双级六连杆传动系统刚度分析研究

杨勇军，高 文，樊 平，张 健，魏春阳

（中车戚墅堰机车有限公司 产品设计部，江苏 常州 213011）

随着经济和技术的发展，列车运行速度越来越高。作为发挥列车牵引动力的铁路机车动力转向架，其驱动系统技术也在不断发展，以适应新的运用要求。对于最高运行速度160～200 km/h 的准高速机车转向架，为减轻簧下质量以达到降低轮轨动作用力的目的，大多采用了轮对空心轴式架悬驱动系统技术，例如DF9、DF11等内燃机车，SS8、SS9等电力机车，以及近几年研发的准高速交流传动机车等。虽然这些机车上的驱动装置具体结构有较大的差异，但轮对空心轴传动机构的结构形式和原理是相同的。

在轮对空心轴式驱动装置技术研究方面，业内技术人员主要开展了驱动装置结构特点及强度、集成应用技术、牵引扭转黏滑振动、驱动装置动力学性能和整车动力学性能等方面的研究［1-4］。针对六连杆传动系统自身刚度特性方面，封全保［5］对传动系统刚度试验方案进行了构思并作了试验研究；钟文生［6］从六连杆运动关系出发讨论了橡胶关节径向刚度特性对横向运动的影响。而轮对空心轴传动系统结构布置尺寸与传动系统各向刚度之间内在规律的研究未见公开报道。为实现精益研发，有必要开展相关研究，一方面为新型轮对空心轴传动系统的研发提供便捷手段，同时也为既有产品的结构优化研究提供理论支撑。

文中将轮对空心轴传动机构作为研究对象，通过经典力学方法对轮对相对于电机的位移和受力情况进行分析，以期摸索出计算轮对空心轴传动机构各向刚度的通用方法。

1 轮对空心轴传动机构原理

1.1 传动机构原理

以DF11机车为例，轮对空心轴架悬式驱动装置由悬挂于转向架上的牵引电动机、牵引齿轮副及齿轮箱、轮对及传动系统组成。传动系统的使用要求：在确保传递牵引电动机牵引扭矩这一功能的前提下，要具有灵活的变位能力，以避免机车动力学性能的恶化。为此，传动系统采用了2 级结构类似的六连杆装置，且每根连杆的两端均装有橡胶关节。牵引扭矩传递路径如图1 所示，电机输出的扭矩经齿轮副传递到从动齿轮辐板后，通过齿轮级六连杆装置传递到空心轴、车轮级六连杆装置，最后传递到车轮上，从而实现轮对与钢轨间黏着牵引力的发挥。

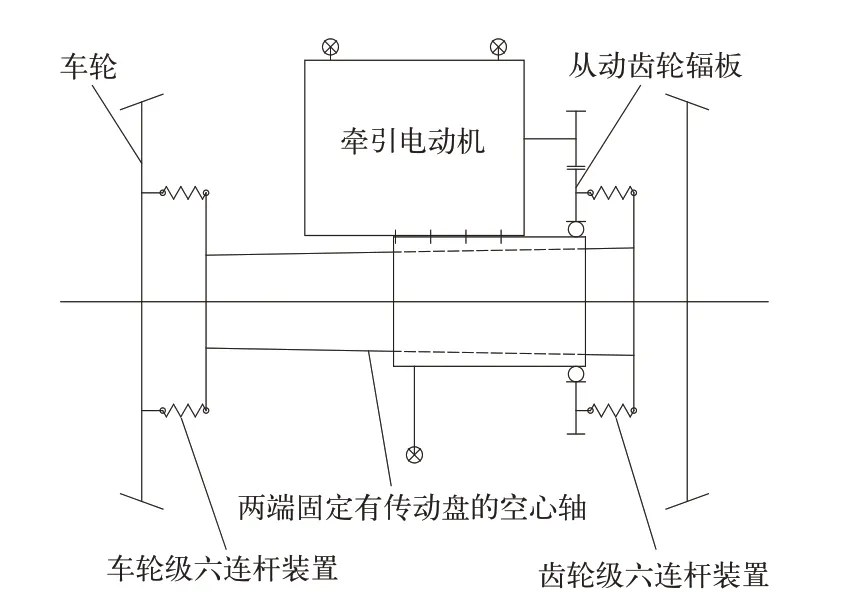
图1 轮对空心轴传动机构原理

对于此类型的驱动系统，从动齿轮除了可相对其轴线作回转运动外，因受结构限制，在垂向、纵向和轴向这3 个方向上可看作与电机同步运动。因此，轮对相对于从动齿轮3 个方向的运动关系也就代表了轮对相对于电机的运动关系。故下文将轮对与从动齿轮之间承担连接作用的空心轴及2级六连杆装置作为分析对象进行受力分析，研究传动系统的各向刚度特性，研究结果可用于评估由于轮对与电机之间相对位移而产生的作用力的大小。

1.2 六连杆布置特征

为保证传递扭矩时各连杆受力均匀，六连杆装置的结构布置必须确保传递任一方向扭矩时，受拉与受压的连杆各3 副互隔、且分别呈120°均布。以下称这一特征为“六连杆均布”。“六连杆均布”的一个特例如图2 所示，即受拉与受压的连杆互隔且各连杆呈60°均布。

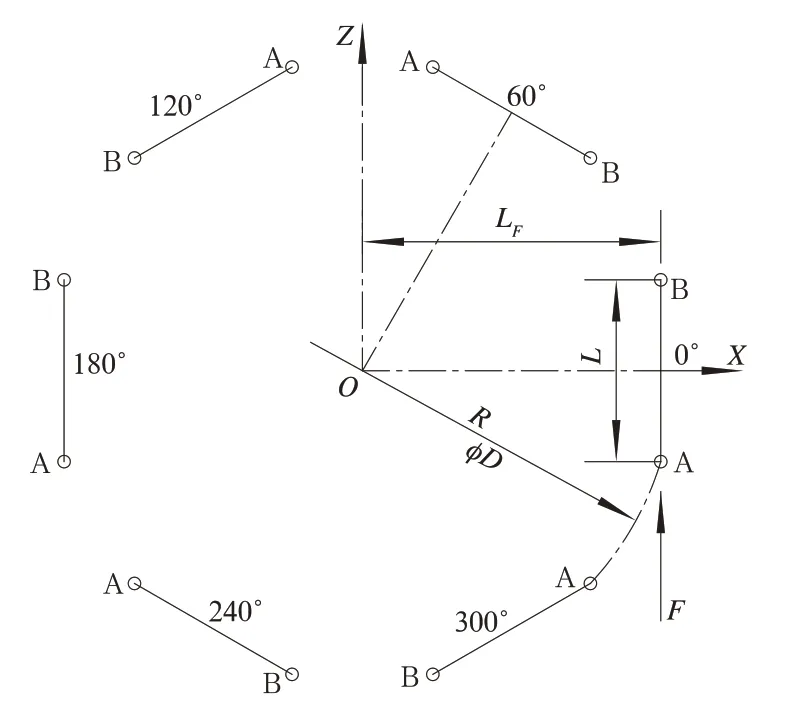
图2 六连杆布置特征

2 连杆各向刚度分析

为方便叙述，文中所指连杆，均包含连杆及其两端的橡胶关节。鉴于连杆是组成空心轴传动机构的基本要素，在分析六连杆装置各向刚度前，先对单一连杆的各向刚度特性进行分析。根据传动机构的运动特点，为简化分析过程，假定同一连杆两端橡胶关节的芯轴始终保持平行；连杆体视为刚体；连杆两端的橡胶关节各向刚度视为恒定值。

2.1 连杆长度方向拉压刚度（纵向刚度）

连杆沿长度方向的拉压刚度，由两端橡胶关节的径向刚度串联构成，为式（1）：

式中：kr-link为连杆长度方向拉压刚度，即连杆纵向刚度；kr为橡胶关节的径向刚度。

2.2 连杆芯轴方向平动刚度（横向刚度）

连杆横向刚度分析如图3 所示，假设连杆A 端芯轴固定，在XOY平面内平行于芯轴方向（Y向）的力F作用下，B 端芯轴横移至B’，且B’相对于B在X向允许位移。现分析B 端芯轴相对于A 端芯轴的横向平动刚度。经分析，可得到式（2）～式（5）：

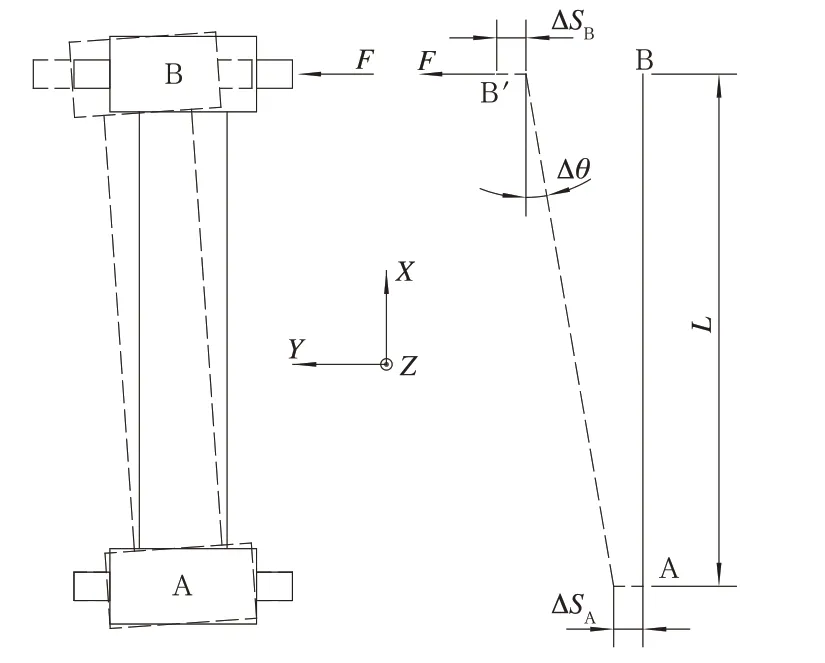
图3 连杆横向刚度分析

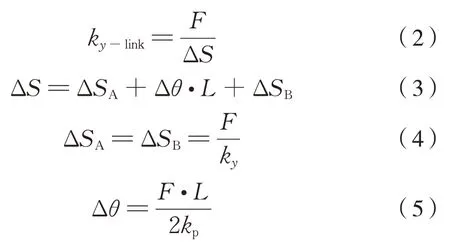
则有式（6）：

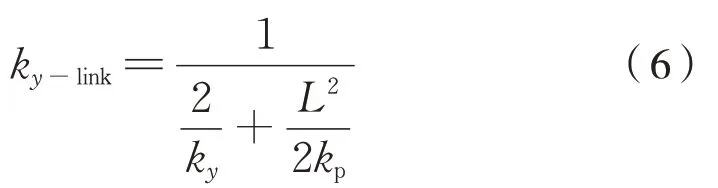
式中：ky-link为连杆一端芯轴相对于另一端在芯轴方向的平动刚度（一根连杆的横向刚度）；L为连杆基准长度；ky、kp分别为橡胶关节的轴向刚度和偏转角刚度。

2.3 连杆平动抗扭刚度

连杆平动抗扭刚度分析如图4 所示，连杆A 端芯轴固定，在ZOX平面内沿芯轴宽度方向（图中Z向）力F作用下，B 端芯轴受结构约束保持平行于A 端芯轴，两芯轴由于相对于连杆体扭转而形成在芯轴宽度方向（即Z向）的相对位移量ΔSt。现分析力F与位移量ΔSt之间的比例关系。

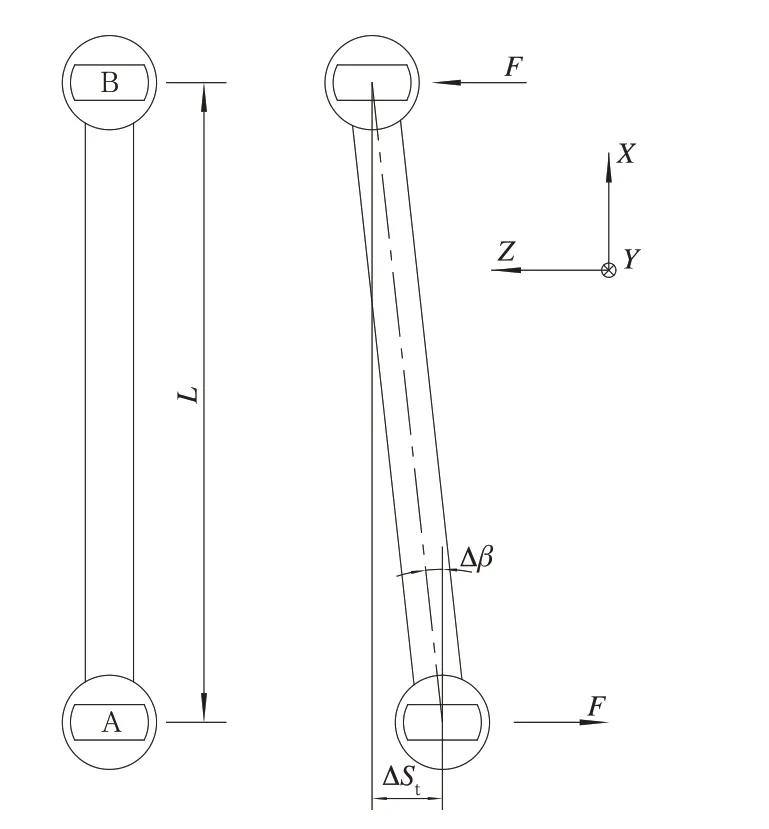
图4 连杆平动抗扭刚度分析

设橡胶关节扭转刚度为kt，则长度为L的连杆、在力F作用下，有式（7）：

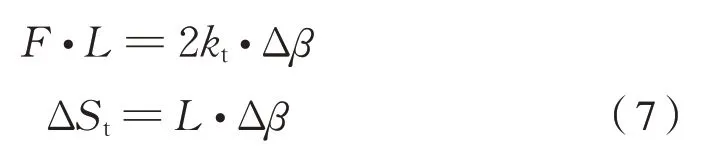
式（7）联解可得两橡胶关节扭转刚度产生的连杆平动抗扭刚度计算为式（8）：

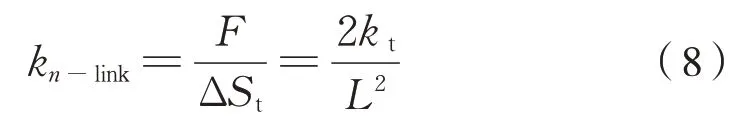
即式（9）：

式中：kn-link为连杆一端芯轴相对于另一端在芯轴宽度方向的平动刚度；kt为橡胶关节的扭转角刚度。

2.4 θ 角体位连杆的两端相对垂向平动刚度

假设一副呈任意θ角体位（以铅垂方向为基准）的连杆，如图5（a）所示，其芯轴A 固定，在垂向力F作用下，芯轴B 因受结构约束，其安装面保持与芯轴A 平行，且只能在垂向产生位移。现分析垂向力F与两芯轴之间垂向位移的比例关系。

作受力分析如图5（b）所示，可得计算式（10）：

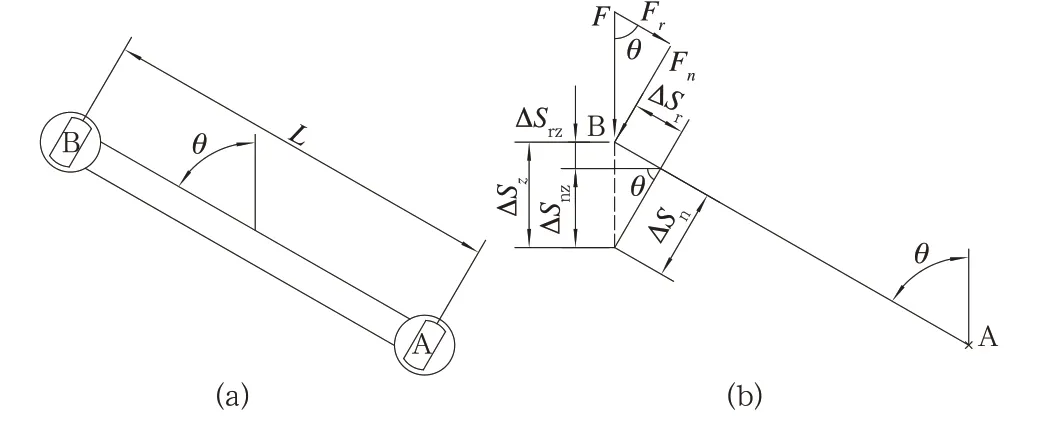
图5 任意θ 角处连杆垂向平动受力分析

则θ角 体 位 连 杆 的 垂 向 平 动 刚 度kz，θ-link计 算公式为式（11）：

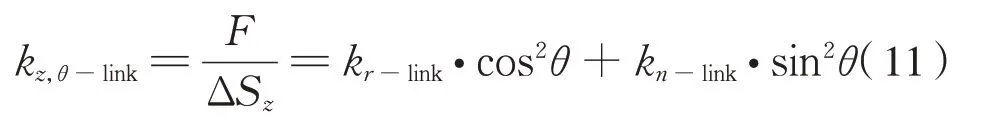
对于橡胶关节径向刚度为kr、扭转刚度为kt的连杆，将式（1）和式（9）代入上式，得到θ角体位连杆的垂向平动刚度计算公式为式（12）：

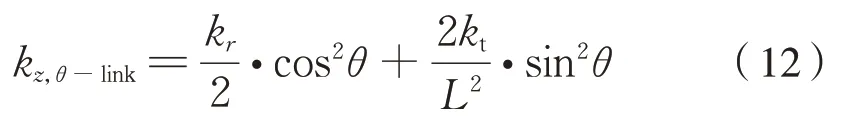
式中：kz，θ-link为θ角 体位 连 杆的 垂向 平动 刚 度；L为连杆基准长度；kr、kt分别为连杆橡胶关节的径向刚度和扭转刚度。

3 传动机构各向刚度分析与计算公式推导

传动机构指由车轮级和齿轮级具有“六连杆均布”特征的六连杆装置及空心轴组成。

3.1 横向刚度

考察六连杆装置的横向（即车轴方向）力传递过程可知，6 副连杆呈并联作用，因此六连杆装置的横向合成刚度计算公式为式（13）：

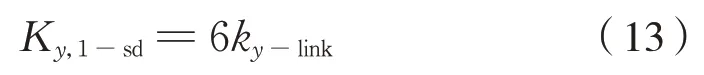
式中：Ky，1-sd为六连杆装置的横向合成刚度；ky-link为一根连杆的横向刚度。

传动机构的横向刚度，由2 级六连杆装置串联构成，故传动机构横向刚度计算为式（14）：

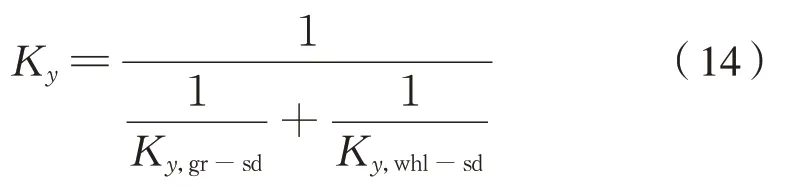
式中：Ky，gr-sd、Ky，whl-sd和Ky分 别为齿 轮级六 连 杆装置的横向合成刚度、车轮级六连杆装置的横向合成刚度和传动机构总的横向合成刚度。

3.2 牵引扭转刚度

根据图2，以齿轮级六连杆装置为例进行扭矩传递过程中的受力分析。设连杆基准长度为L、两端关节中心布置在半径为R的圆周上，在传递扭矩6Mlink时，每根连杆传递的拉力或压力均为F。则力F对圆心O 点的力臂长度LF及力矩Mlink为式（15）、式（16）：

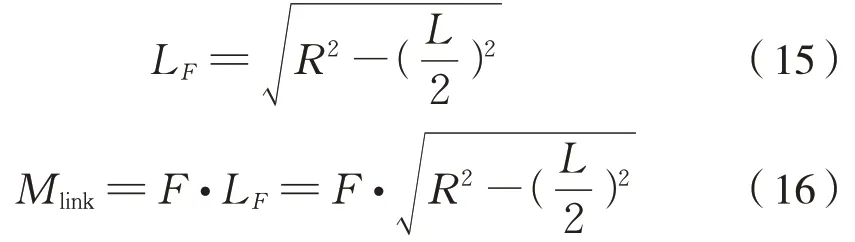
设六连杆装置传递的总力矩为M1-sd、从动齿轮相对于空心轴（传动盘）绕圆心O 点回转角位移为Δβ1-sd，则M1-sd、Δβ1-sd及从动齿轮位于半径LF处的切向位移Δr的计算式为式（17）、（18）、（19）：

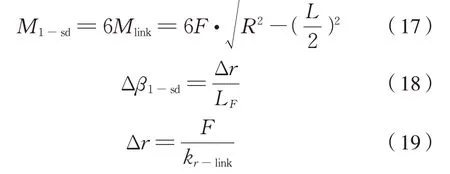
则六连杆装置牵引扭转刚度Kt，1-sd为式（20）：

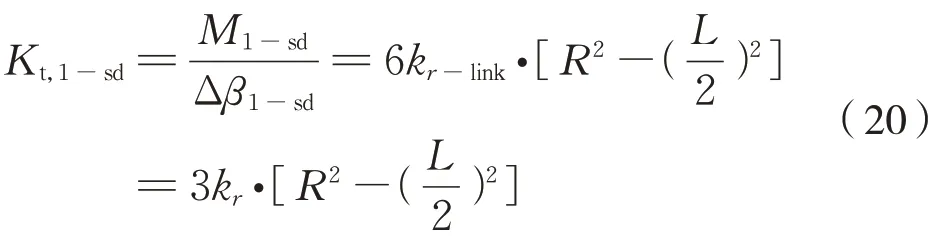
这就得到1 级六连杆装置的合成牵引扭转刚度为式（21）：

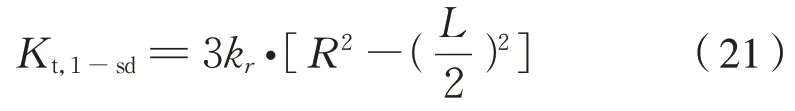
式 中：Kt，1-sd为 六 连 杆 装 置 的 牵 引 扭 转 刚 度；kr为橡胶关节径向刚度；L、R分别为连杆基准长度和传动销定位圆半径。

因此传动机构的合成牵引扭转刚度由2 级六连杆装置串联构成为式（22）：

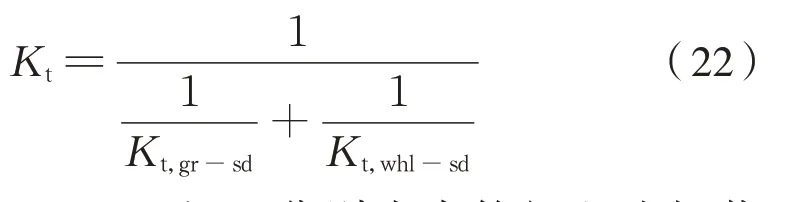
式 中：Kt，gr-sd、Kt，whl-sd和Kt分 别 为 齿 轮 级 六 连 杆 装置的扭转刚度、车轮级六连杆装置的扭转刚度和传动机构扭转刚度。

3.3 垂向刚度

从动齿轮相对于车轮的垂向位移可看成是2级六连杆装置的垂向平动位移与空心轴侧滚位移相叠加而成。以下分别分析这2 种情况。

（1）考虑六连杆装置垂向平动

前文已分析了处于任意θ角的连杆受力情况，得到了连杆两端芯轴相对垂向平动时的刚度计算公式（12）。对于图2 所示六连杆装置，其垂向合成平动刚度只需将处于不同θ角的6 副连杆的垂向平动刚度进行叠加即可，即六连杆装置的垂向平动刚度为式（23）：

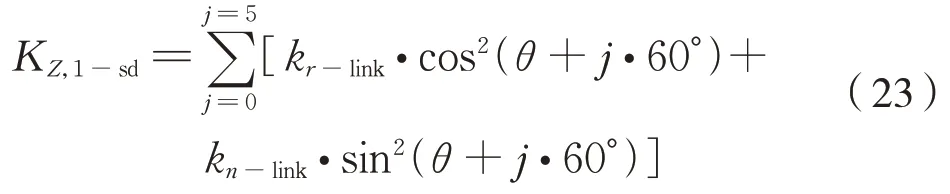
简化得式（24）：

将式（1）和式（9）代入式（24），就得到六连杆装置在仅考虑纯垂向平动时的刚度为式（25）：

式中：KZ，1-sd为六连杆装置仅考虑垂向平动的刚度；kr、kt、L分别为橡胶关节的径向刚度、扭转刚度和连杆基准长度。

可以证明，式（25）适用于所有具有“六连杆均布”特征的六连杆装置。

（2）考虑空心轴侧滚（从动齿轮与车轮保持相对平行）

空心轴侧滚示意图如图6 所示，由于空心轴相对于从动齿轮产生侧滚角位移α，6 根连杆的B 端关节相对于A 端关节有大小不一的横向位移。空心轴侧滚刚度分析如图7 所示，假设某连杆A 端芯轴连接在从动齿轮上，B 端芯轴固结在传动盘（与空心轴固定）上，那么B 点相对于传动盘中心的位置可用极坐标（R，θ’）表示。则B 端芯轴相对于A端芯轴横移量ΔSy为式（26）：

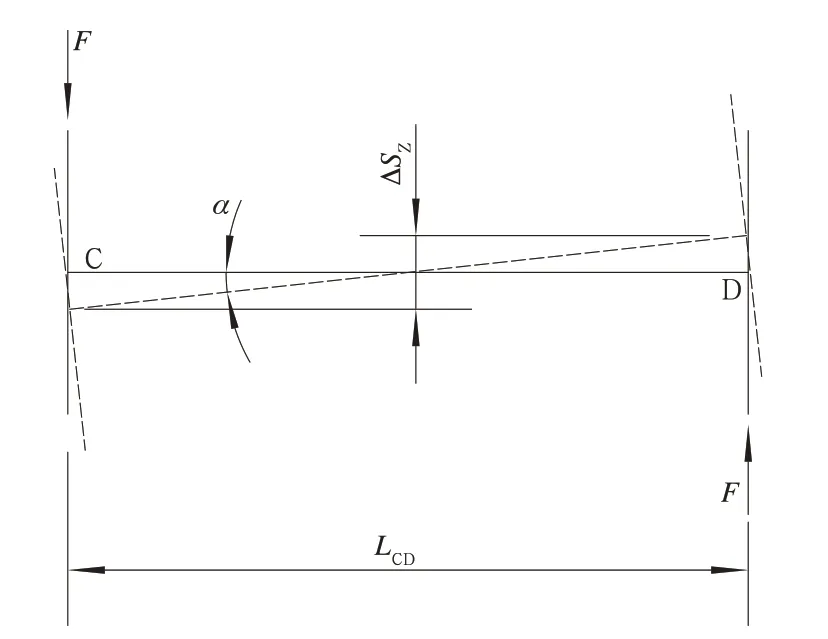
图6 空心轴侧滚示意图

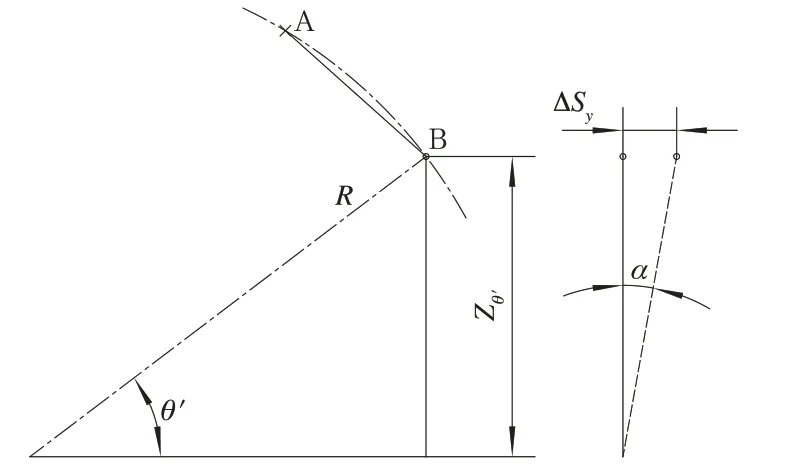
图7 侧滚刚度分析

式中：Zθ′=R⋅sinθ′ 。

对于横向刚度为ky-link的连杆，两端相对横移ΔSy时的复原力Fy，θ′为式（27）：

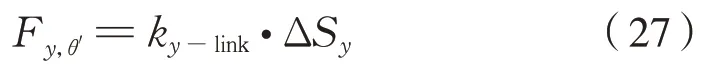
由此产生的侧滚复原力矩Mθ′、进而得到该连杆的侧滚刚度kθ′，roll计算公式为式（28）～式（29）：

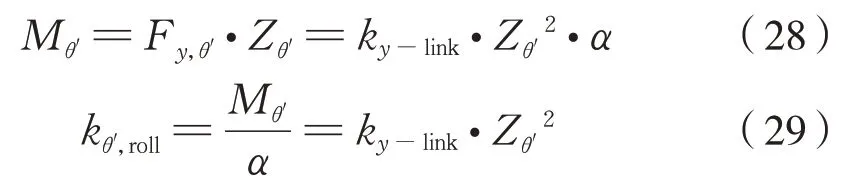
代入Zθ′得到式（30）：

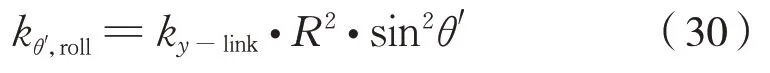
则六连杆装置的合成侧滚刚度Kroll，1-sd为式（31）：

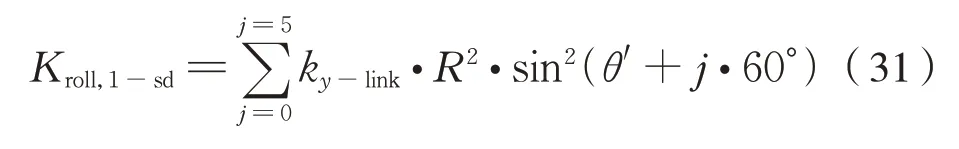
经简化得到式（32）：

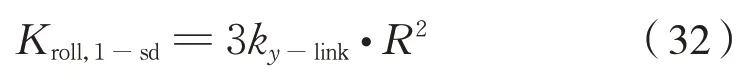
式 中：Kroll，1-sd为 单 级 六 连 杆 装 置 侧 滚 刚 度；ky-link、R分别为连杆横向刚度和传动销定位圆半径。

可以证明，式（32）适用于所有具有“六连杆均布”特征的六连杆装置。

空心轴侧滚刚度由齿轮侧和车轮侧2 级六连杆装置侧滚刚度并联得到，即为式（33）：

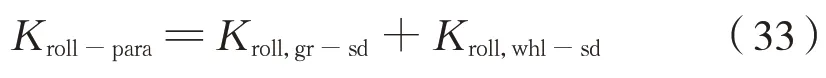
式 中：Kroll-para为 空 心 轴 侧 滚 刚 度；Kroll，gr-sd、Kroll，whl-sd分别为齿轮侧和车轮侧六连杆装置的侧滚刚度。

由图6 可知，对于横向跨距LCD的2 级六连杆装置，侧滚α时两侧高度差ΔSz为式（34）：

考虑整套传动机构力矩平衡，有式（35）：

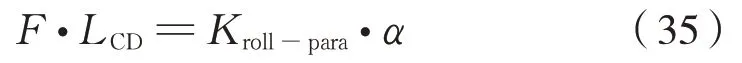
因而可得到传动机构在考虑空心轴侧滚时的垂 向 刚 度Kz，roll为：

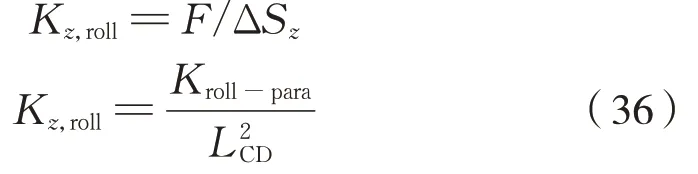
（3）合成垂向刚度

将车轮侧、齿轮侧六连杆装置垂向平动刚度和考虑空心轴侧滚的传动机构垂向刚度串联计算，可得到传动机构合成垂向刚度Kz，即有式（37）：

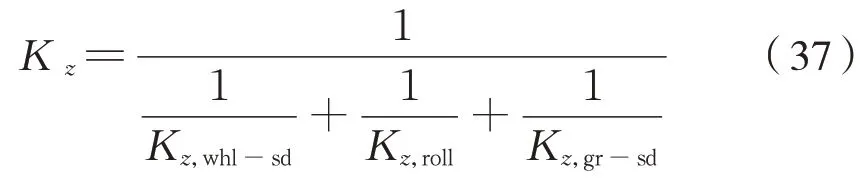
式 中：Kz，whl-sd、Kz，gr-sd分 别 为 车 轮 级 和 齿 轮 级 六 连杆装置垂向平动刚度，值按式（25）计算。

从前述分析过程以及推导得到的相关公式可以看出，传动机构合成垂向刚度与机车行进过程中轮对旋转的瞬时角度无关，即径向同性。

3.4 纵向刚度

由于2 级六连杆均布，传动机构纵向刚度与垂向刚度相同，即为同一径向刚度。

3.5 侧滚刚度

前文对空心轴侧滚运动作了分析，推导出了单级六连杆装置侧滚刚度计算公式，即式（32）。而传动机构总的侧滚刚度，考察的是从动齿轮相对于车轮发生侧滚的情况，即将2 级六连杆装置侧滚刚度作串联计算，得式（38）：

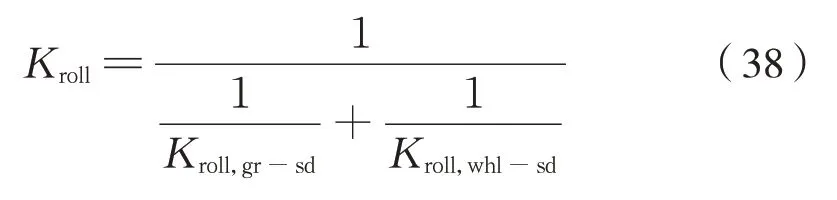
4 计算实例

以某宽轨准高速机车转向架轮对空心轴传动系统为例，利用前文推导出的计算公式对传动机构各向刚度进行了计算。已知条件见表1，各刚度计算结果见表2。

表1 实例主要参数

5 仿真验证

为验证推导出的传动机构各向刚度计算公式的准确性，利用SIMPACK 动力学分析软件对第4节给出的传动系统建立了详细仿真模型；并基于常见工况对各向刚度进行了动力学仿真分析。仿真结果及与利用刚度公式计算结果的对比情况见表2。可以看出，2 种方法得到的结果最大偏差仅7.8%，吻合良好，表明刚度计算公式是准确的。

表2 2 种方法得到的传动机构各向刚度结果比较

关于仿真分析，需要补充说明的是：（1）仿真得到的横向刚度随相对横向位移量的增大而增大，但增大幅度不超过2%；表中列出的仿真刚度值是偏离静态平衡位置较小位移下的仿真值。（2）从文中实例来看，虽然径向刚度和侧滚刚度仿真结果与刚度公式计算结果相差约8%，但两者的数值均很小，对动力学性能的影响可以忽略。

6 结 论

利用经典力学方法推导出了轮对空心轴六连杆传动机构各向刚度的计算公式。运用这些公式，可大大简化传动系统的力学模型，提高驱动装置方案对比研究和优化的工作效率。

为验证刚度公式的准确性，用SIMPACK 软件建立了传动系统的仿真模型，经过一系列典型工况的仿真分析，证实了在常见位移范围内空心轴传动机构各向刚度可视作常值，表明利用经典力学方法推导出统一的刚度公式来计算所需刚度这一做法是可行的。仿真得到的刚度与利用公式计算出的刚度吻合较好，表明刚度公式的准确性满足工程应用需要。