机车抗蛇行减振器参数对临界速度的影响分析*

张喜清，蔡松岩，李幸人，史青录，张宏伟

（1 太原科技大学 机械工程学院，太原 030024；2 中车大同电力机车有限公司 技术中心，山西 大同 037038）

由于各国轨距不同，其中俄罗斯及周边国家采用轨距1 520 mm 的宽轨铁路，与我国的1 435 mm 标准轨距铁路有所不同，在设计方面将会面临诸多问题［1］。抗蛇行减振器是高速轨道车辆转向架二系悬挂的重要组成部分，可以显著提高临界速度，对转向架的横向稳定性影响非常明显［2］。因此，研究抗蛇行减振器参数对宽轨电力机车动力学性能的影响非常必要。丁雪萍等［3］利用SIMPACK 分析抗蛇行减振器阻尼和一系悬挂参数的变化对宽轨机车动力学性能的影响。周素霞等［4］利用SIMPACK 分析了抗蛇行减振器故障对车辆各项动力学性能的影响，得出了抗蛇行减振器最佳阻尼特性。王攀攀等［5］考虑多种设计参数，构造悬挂参数多目标6σ稳健优化基本模型，获得悬挂参数多目标稳健优化结果。文献［6-8］研究了抗蛇行减振器阻尼与刚度等参数对列车横向稳定性的影响。文献［9］研究了串联节点刚度对隔振系统传递率的影响。文献［10-12］运用解析设计方法和SIMPACK 等轨道车辆动力学分析软件研究了列车的横向动力学性能和曲线通过性，从而进行抗蛇行减振器阻尼特性参数的设计。文献［13］利用转向架回转阻力矩测试试验台分析了轨道车辆的曲线通过性。

国内对于宽轨电力机车的临界速度的研究相对较少，且大多是针对其单个参数对车辆临界速度的影响，而没有考虑到二系横向刚度和抗蛇行减振器参数的匹配问题。文中以宽轨电力机车为研究对象，将抗蛇行减振器精细概念模型等效为Maxwell 模型，建立了带二系悬挂的刚性转向架动力学模型。利用蛇行运动线性稳定性理论，推导了该转向架模型的临界速度计算方程，研究了不同二系横向刚度下，抗蛇行减振器串联刚度和结构阻尼对临界速度的影响，为宽轨电力机车抗蛇行减振器参数的设计提供了理论支撑。

1 抗蛇行减振器Maxwell 等效模型

抗蛇行减振器是机车二系悬挂的重要组成部分，可以显著提高临界速度。抗蛇行减振器通常为液压减振器，液压减振器在动力学计算中一般采用一个阻尼元件来描述，但在工程实际中液压减振器的安装座、橡胶节点、油液均存在一定刚度，使得减振器在轴向运动时具有弹性，表现出一定的刚度效应，导致阻尼力和活塞速度出现相位差，此时减振器阻尼表现出动态特性。抗蛇行减振器的精细概念模型如图1 所示，抗蛇行减振器水平纵向地安装于车体与转向架构架之间，由阻尼元件、刚度元件和间隙元件串联组成。其中间隙元件为减振器安装间隙lgap；刚度元件分别为安装座刚度kseat、橡胶节点刚度krubber、油液刚度koil；阻尼元件为减振器内部结构阻尼c。

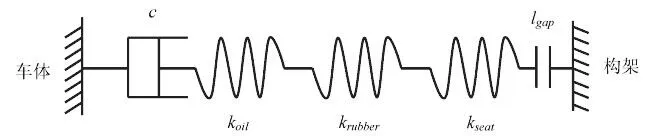
图1 抗蛇行减振器精细概念模型

一般情况下安装间隙小于1 mm，可忽略其安装间隙，并将油液刚度、橡胶节点串联刚度和安装座刚度等效为总的抗蛇行减振器串联刚度k，为式（1）：

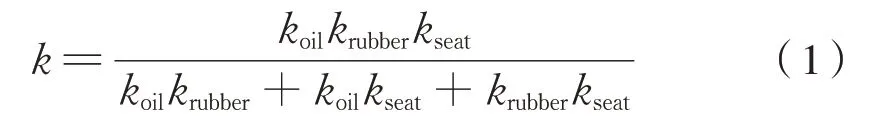
则上述的抗蛇行减振器精细概念模型可以等效为一个串联刚度k和结构阻尼c串联的Maxwell模型，如图2 所示。

图2 抗蛇行减振器Maxwell 模型

由图2 中的模型可知，抗蛇行减振器端部受到位移正弦激励x，其振幅A，频率ω，x=Asin（ωt），活塞质量m，可列出该模型的振动方程为式（2）：

由于m很小，可以忽略惯性力，则式（1）改为式（3）：

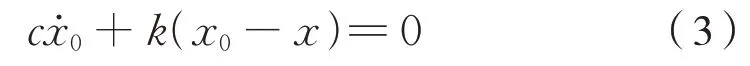
根据微分方程求解得式（4）：

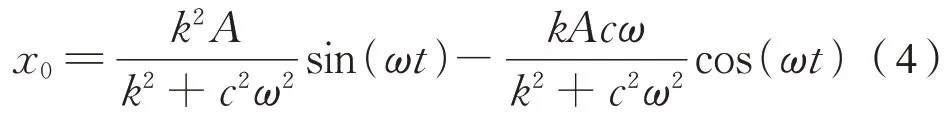
则减振器的阻尼力可以表示为式（5）、式（6）：

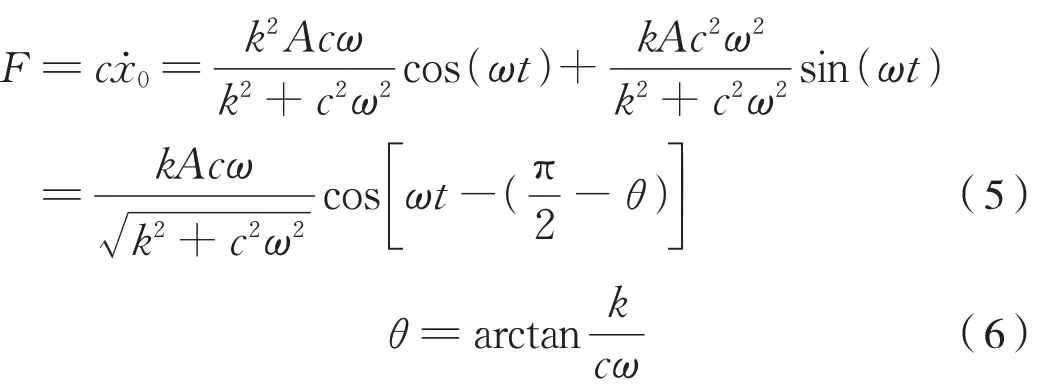
将x=Asin（ωt）带入式（4），得式（7）：

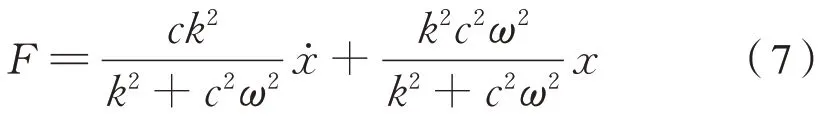
则等效刚度和等效阻尼系数为式（8）：

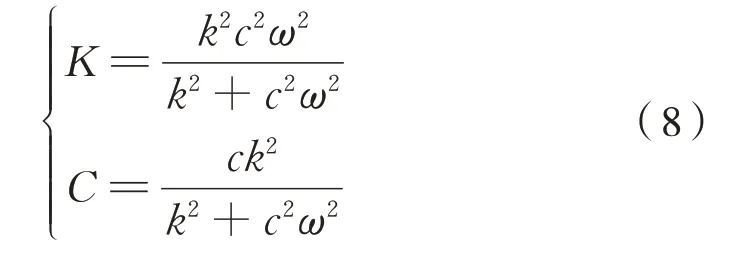
由式（7）可知，Maxwell 模型的抗蛇行减振器阻尼力是随激振角频率动态变化的，可得该模型在不同激励频率下的示功图，如图3 所示。

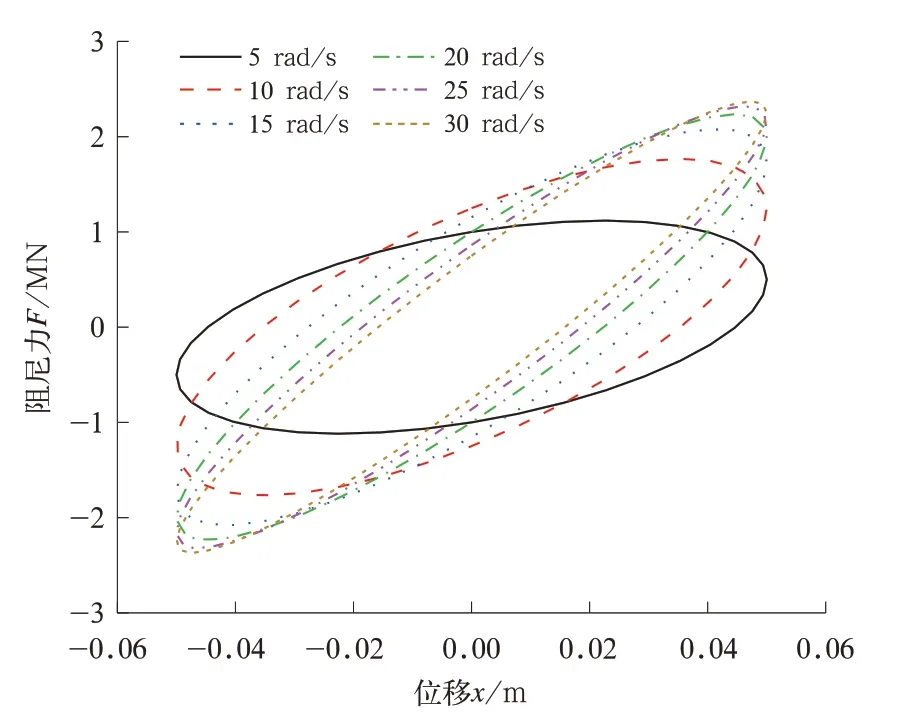
图3 激振角频率对示功图的影响

从图3 可以看出，由于Maxwell 模型阻尼力和速度之间有相位角，其示功图为一个存在一定倾斜角的椭圆，即减振器的滞回曲线，椭圆的面积表示阻尼力做的功。在一定的结构阻尼和串联刚度下，激励角频率越大，椭圆的倾斜角度越大，阻尼力峰值越大，即随激振角频率呈动态阻尼特性。

为进一步具体分析激振角频率对等效刚度和等效阻尼的影响，取抗蛇行减振器结构阻尼作为定值5 MNs/m，将串联刚度分为6 组，通过式（7）计算得到不同串联刚度下，等效刚度和等效阻尼随激励角频率变化的频响特性曲线，如图4 所示；然后将串联刚度定为20 MN/m，将结构阻尼分为6组，计算出不同结构阻尼下，等效刚度和等效阻尼随激励角频率变化的频响特性曲线，如图5 所示。

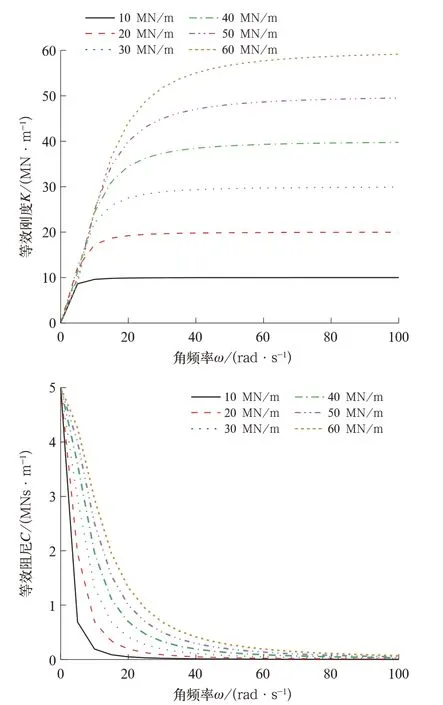
图4 不同串联刚度的频率响应特性

由图4 和 图5 可 知，在 低频激 励 下，Maxwell 模型表现出小等效刚度大等效阻尼的特性，不同串联刚度下的等效刚度都非常小，等效阻尼接近于结构阻尼，此时Maxwell 模型近似表现为纯阻尼模型，此特性有利于在曲线工况下的通过性能；随着激振角频率增大，等效刚度先增大，然后趋于稳定值，结构阻尼减小直至趋于0；在高激振角频率区间，模型表现出大等效刚度小等效阻尼的特性，等效刚度近似等于串联刚度，模型表现为纯刚度无阻尼模型，此时应采用高频卸荷的方法保护减振器结构元件。在一定研究参数范围内，角频率激励一定时，等效刚度随串联刚度和结构阻尼的增大而增大；等效阻尼随串联刚度的增大而增大，且在激励角频率低于10 rad/s 时随结构阻尼的增大而增大，在激励角频率高于10 rad/s 时随结构阻尼的增大而减小。

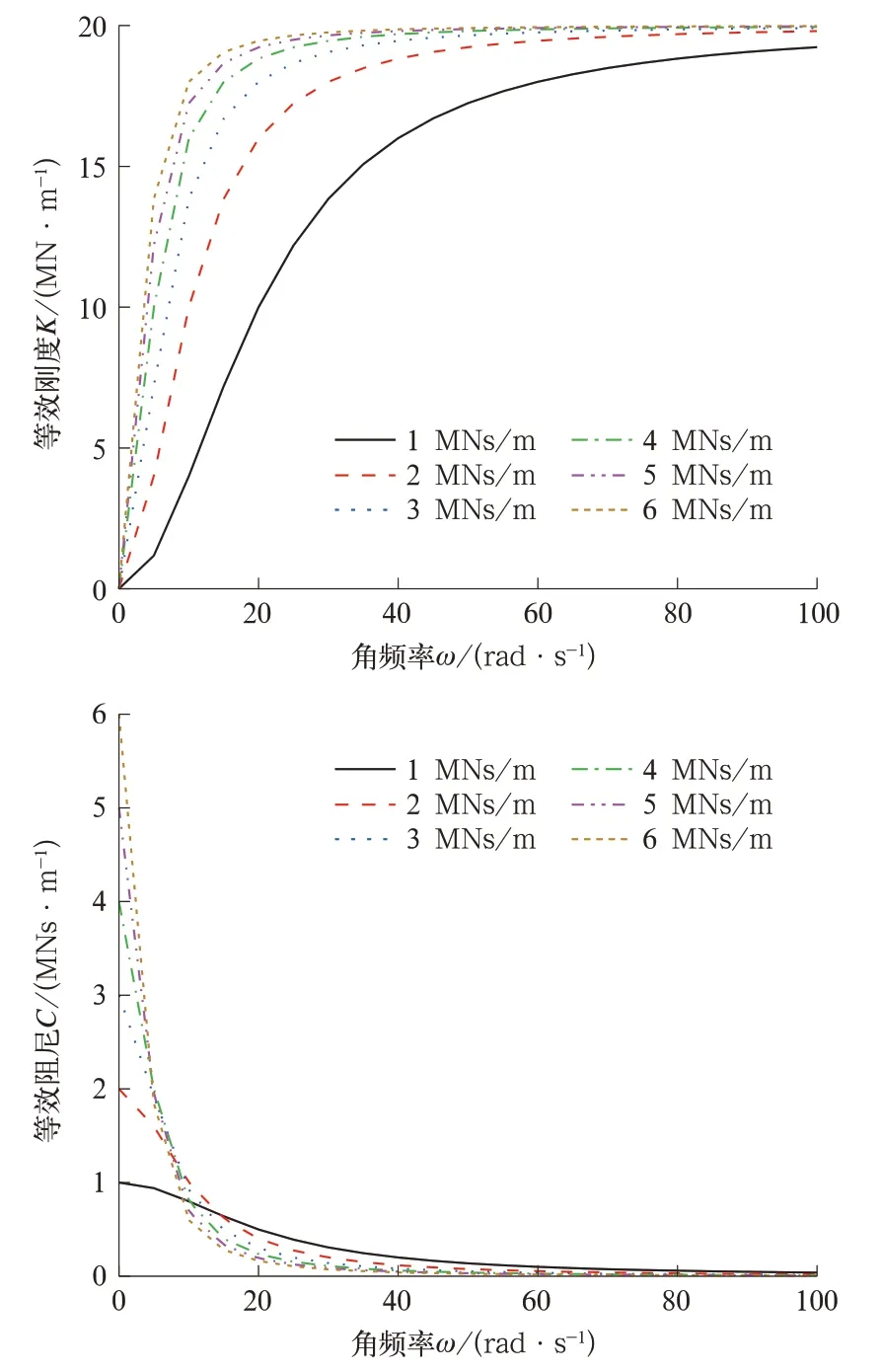
图5 不同结构阻尼的频率响应特性

2 三轴刚性转向架临界速度分析模型

实际的轨道车辆转向架系统非常复杂，转向架一系定位有多种方式，为取得更高的临界速度，一系定位刚度通常较大，一系定位刚度越大则越接近刚性转向架，为了对转向架临界速度进行理论分析，突出研究重点，将某型宽轨电力机车三轴转向架简化为刚性转向架，重点研究二系横向刚度和抗蛇行减振器参数的匹配对转向架临界速度的影响。

2.1 数学模型

临界速度问题属于横向动力学范畴，与垂向自由度相关度较低，且文中只研究转向架横向稳定性，不考虑车体自由度，车体只作为参考系沿轨道以恒定速度直线行驶。综上考虑，以转向架构架的质心O为坐标原点，以垂直于车辆行驶方向向右及沿车辆行驶方向顺时针的方向为横摆运动和摇头运动的正方向，研究带二系悬挂的三轴刚性转向架，横向减振器和抗蛇行减振器一端连接构架，另一端连接车体，考虑构架的横移和摇头。轮轨力的处理采用Hertz 接触理论和Kalker 线性蠕滑理论，不考虑自旋蠕滑，踏面为经典锥形踏面，车辆沿轨道直线匀速行驶。三轴刚性转向架蛇行运动模型如图6 所示。

图6 中，M为刚性转向架质量；b为滚动圆横向跨距之半；b1为抗蛇行减震器安装点横向距离之半；l1为前轴至中间轴的轴距；l2为后轴至中间轴的轴距；k为抗蛇行减振器Maxwell 模型的减振器串联刚度；c为抗蛇行减振器Maxwell 模型的结构阻尼；ky为二 系 横 向 刚度；cy为 二 系横 向阻 尼；φ为 构架摇头角。

图6 三轴刚性转向架蛇行运动模型

2.2 转向架运动微分方程

根据上述二自由度三轴刚性转向架分析模型，忽略轮轨耦合作用及减振器质量，建立其运动微分方程为式（9）：

式中：f11为纵向蠕滑系数；f22为横向蠕滑系数；K为抗蛇行减振器等效刚度；C为抗蛇行减振器等效阻尼；λ为踏面锥度；r为车轮名义滚动圆半径；J为刚性转向架摇头转动惯量；y为构架横移。

将式（7）代入式（8）进行降阶，可得到其Jacobi矩阵A式（10）：

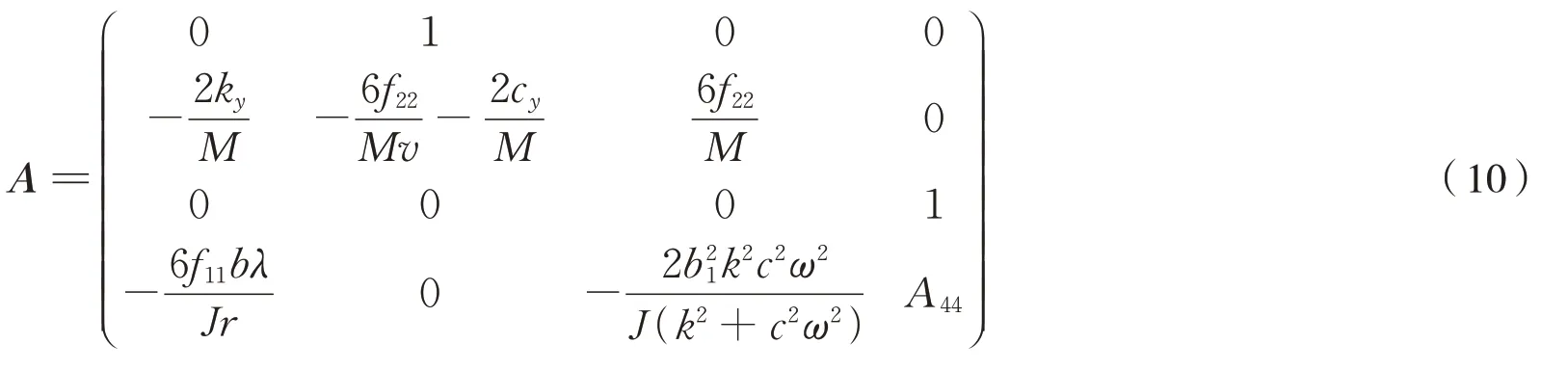
式中：

其对应的特征方程为式（11）：

设a0、a1、a2、a3、a4为式（12）：

特征方程可以写为式（13）：

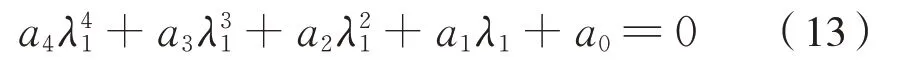
令特征方程的根为式（14）：

据稳定性理论，当到达临界速度时，式（13）有一对纯虚根，且其余根具有负实部，即λ1=iω，代入式（13）并求解可得式（15）：

ω1为构架在临界速度下的蛇行角频率，由于三轴刚性转向架的蛇行角频率可有如下近似式（16）：

即ω1=ω。 可得转向架临界速度方程为式（17）：

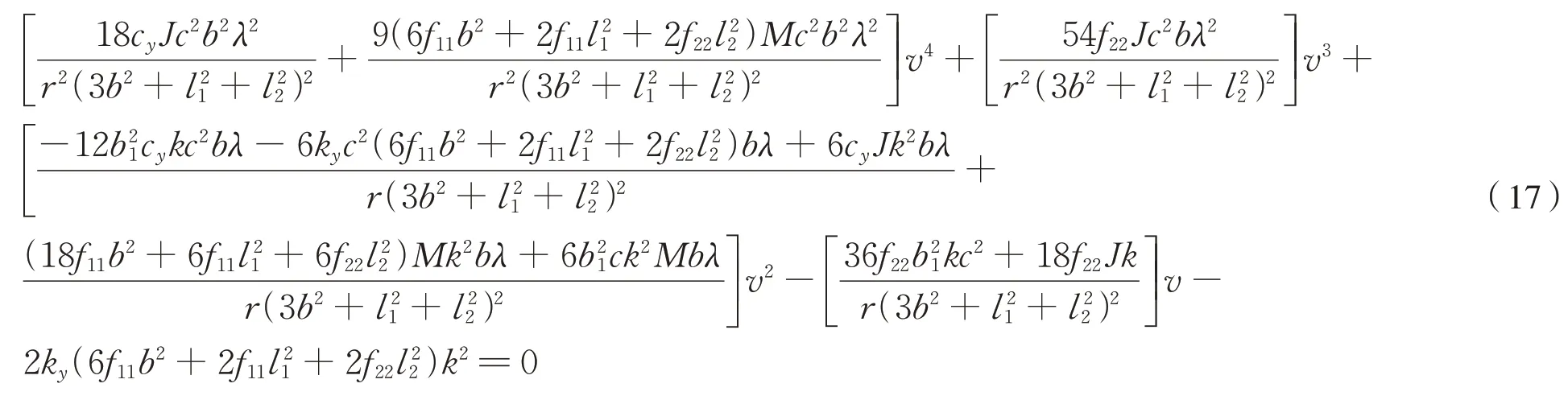
3 参数对临界速度影响分析

根据上述建立的临界速度方程，以某型出口白俄罗斯的宽轨电力机车为研究对象，其设计速度为120 km/h，原始参数见表1，对其进行临界速度计算分析。

3.1 二系横向刚度和结构阻尼对临界速度的影响

选抗蛇行减振器串联刚度为10、50、100 MN/m这3 组情况，利用式（17）的临界速度方程，计算分析不同二系横向刚度下，抗蛇行减振器的结构阻尼对临界速度的影响，如图7 所示。

由图7 可知，在一定的参数变化范围内，在相同串联刚度和结构阻尼下，二系横向刚度越大，车辆的线性临界速度越高，且随着结构阻尼的增大越容易趋向于稳定值，即在较小的结构阻尼下临界速度便不再随结构阻尼的增大而有明显提高，可见二系横向刚度较小时，与其匹配的结构阻尼应较大，二系横向刚度较大时，与其匹配的结构阻尼应较小。

图7 抗蛇行减振器的结构阻尼对临界速度的影响

在3 组串联刚度下，临界速度都随着结构阻尼的增大而增大，然后逐渐趋于稳定值，并有其对应的结构阻尼饱和值。虽然变化趋势基本一致，但在变化的速率和幅度上略有不同。串联刚度为10 MN/m 时，临界速度在2～4 MNs/m 的结构阻尼下便趋于稳定值；串联刚度为50 MN/m 时，随着结构阻尼的逐渐增大，临界速度先缓慢提高，然后提高速度明显加快，最后在8～10 MNs/m 的结构阻尼下趋于稳定值，增长趋势呈S 型；串联刚度为100 MN/m 时，随结构阻尼的增大，在18～20 MNs/m的结构阻尼下趋于稳定值，临界速度的增长趋势也呈S 型。可见，串联刚度越大，其临界速度稳定值对应的阻尼饱和值越大。另外，在2～4 MNs/m的结构阻尼下，串联刚度为10 MN/m 时的临界速度最大，串联刚度为50 MN/m 时的临界速度次之，串联刚度为100 MN/m 时的临界速度最小；在结构阻尼大于8 MNs/m 时，串联刚度为100 MN/m 时的临界速度最大，串联刚度为50 MN/m 时的临界速度次之，串联刚度为10 MN/m 时的临界速度最小。

3.2 二系横向刚度和串联刚度对临界速度的影响

设抗蛇行减振器结构阻尼为4、8、10 MNs/m，利用式（17）的临界速度方程，计算分析不同二系横向刚度下，抗蛇行减振器的串联刚度对临界速度的影响，如图8 所示。

由图8 可知，串联刚度和结构阻尼一定的情况下，二系横向刚度越大，车辆的线性临界速度越大，且线性临界速度峰值对应的串联刚度越大，因此，二系横向刚度较小时，与其匹配的串联刚度应较小，二系横向刚度较大时，与其匹配的串联刚度应较大。

图8 抗蛇行减振器的串联刚度对临界速度的影响

在3 组结构阻尼下，线性临界速度均随着串联刚度的增大而先提高后降低，存在临界速度峰值及其所对应串联刚度最优值，虽然变化趋势基本一致，但在变化的快慢和大小上略有不同。结构阻尼为4 MNs/m 时，临界速度在串联刚度达到20～40 MN/m 时便达到临界速度峰值；结构阻尼为8 MNs/m 时，临界速度在串联刚度达到60～80 MN/m 时才达到临界速度峰值；结构阻尼为10 MNs/m 时，临界速度在串联刚度达到90 MN/m以上时才达到临界速度峰值，可以看出，结构阻尼越大，达到临界速度峰值时的串联刚度最优值越大，则与之匹配的串联刚度应越大，结构阻尼越小，与之匹配的串联刚度应越小。

综合3.1 节与3.2 节中抗蛇行减振器参数对临界速度的影响规律，对于该型宽轨电力机车，其二系横向刚度为420 MN/m，为获得较高的安全裕度，抗蛇行减振器串联刚度的取值应在50 MN/m和80 MN/m 之间，结构阻尼取值应大于8 MNs/m，为兼顾机车运行平稳性，建议取抗蛇行减振器串联刚度为50 MN/m，结构阻尼为8 MNs/m，此时临界速度高于150 km/h，满足120 km/h 的运行需求。

4 结 论

文中针对宽轨电力机车，利用抗蛇行减振器的等效Maxwell 模型，建立了带二系悬挂的三轴刚性转向架二自由度蛇行运动模型，推导出其线性临界速度方程。在此基础上，研究了不同二系横向刚度下抗蛇行减振器串联刚度和结构阻尼对临界速度的影响，所得结论如下：

（1）在抗蛇行减振器串联刚度确定的情况下，车辆的线性临界速度随着结构阻尼值的增大而提高，且存在临界速度峰值和其对应的结构阻尼饱和值。车辆的二系横向刚度越大，其对应的结构阻尼饱和值越小；二系横向刚度越小，其对应的结构阻尼饱和值越大。

（2）在抗蛇行减振器结构阻尼确定的情况下，车辆的线性临界速度随着串联刚度的增大先提高后降低，存在临界速度峰值和其对应的串联刚度最优值。二系横向刚度越大，其对应的串联刚度最优值越大；二系横向刚度越小，其对应的串联刚度最优值越小。串联刚度较大时，应匹配较大的结构阻尼；串联刚度较小时，应匹配较小的结构阻尼。

（3）在文中研究的参数范围内，为达到更高的临界速度，不同的二系横向刚度应匹配不同的串联刚度和结构阻尼，二系横向刚度较大时，与其匹配的串联刚度应较大、结构阻尼应较小，二系横向刚度较小时，与其匹配的串联刚度应较小、结构阻尼应较大。

（4）针对文中的宽轨电力机车，建议取抗蛇行减振器串联刚度50 MN/m，结构阻尼8 MNs/m，此时临界速度高于150 km/h，满足120 km/h 的运行需求。