城轨车辆永磁同步电机转子位置角度校正研究
2022-09-07赵立洋李鹤群王智鹏高宏洋
赵立洋,李鹤群,王智鹏,高宏洋
(中车大连电力牵引研发中心有限公司,辽宁 大连 116052)
永磁同步电机体积小,质量轻,效率高,近年来在城市轨道交通领域应用日益广泛。永磁同步电机控制的基础是获取准确的转子位置角度。然而在实际控制中,由于采集的转子位置带有误差,因此降低了控制系统的输出精度,严重时会影响电机运行的稳定性[1]。需要对转子位置角度误差进行分析和补偿校正,避免在控制过程中使用带有误差的位置角度进行控制而引入的系统噪声,提升控制系统输出精度,抑制电机转矩波动,提升车辆运行的平稳性。
1 原理设计
1.1 转子位置角度误差及影响分析
永磁同步电机一般采用矢量控制方式。矢量控制通过坐标变换将电机三相交流电流转换为旋转坐标系下的直流电流,只需控制电流的转矩电流分量iq和弱磁电流分量id,就能够达到类似于控制直流电机的效果,具有动态响应速度高、转矩脉动小的优点,能够迅速调整牵引电机的转矩输出状态[2]。
矢量控制对永磁同步电机转子位置角度依赖很强,在其坐标变换的过程中需要使用电机的转子位置角度。如果转子位置角度不准确,则会对电机控制效果造成影响。
由于在永磁电机矢量控制中,d轴电流id和q轴电流iq是通过park 变换把静止坐标系下的iα和iβ变换为旋转坐标系下的id和iq,在此过程中需要使用电机转子的位置角度,即旋转坐标系d轴和静止坐标系α轴的夹角θ[3]。
park 变换公式为式(1):
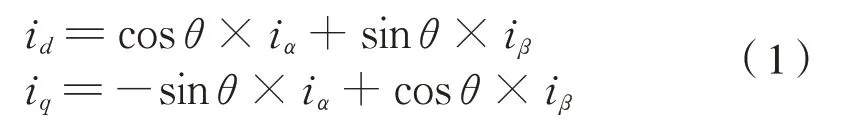
城轨永磁同步电机一般采用旋转变压器采集转子位置角度信息,旋转变压器在电机运行时反馈高频交流信号,经过特定解码芯片解码后,高频交流信号被转换成数字信号送入控制器。解码后的数字信号的范围是0~4 095,对应转子位置从0°~360°变化[4]。
在实际工程项目中,控制器采集到的转子位置角度一般会带有一定误差,这种误差来自于旋转变压器制造过程中的工艺水平、转子安装时的安装精度以及旋转变压器反馈信号波形受到车辆电气系统干扰产生的畸变等[5]。
永磁同步电机旋转变压器的反馈经解码后由控制器读取的波形如图2 所示。从直观上看,采集到的转子位置角度是在0~4 095 之间呈周期性变化的锯齿波。对此波形进行分析,可以得到所采集的波形与理想的波形间的误差分布,如图3 所示。可见,转子位置角度的采集误差仅凭波形无法直观看出。

图2 旋转变压器采集的波形
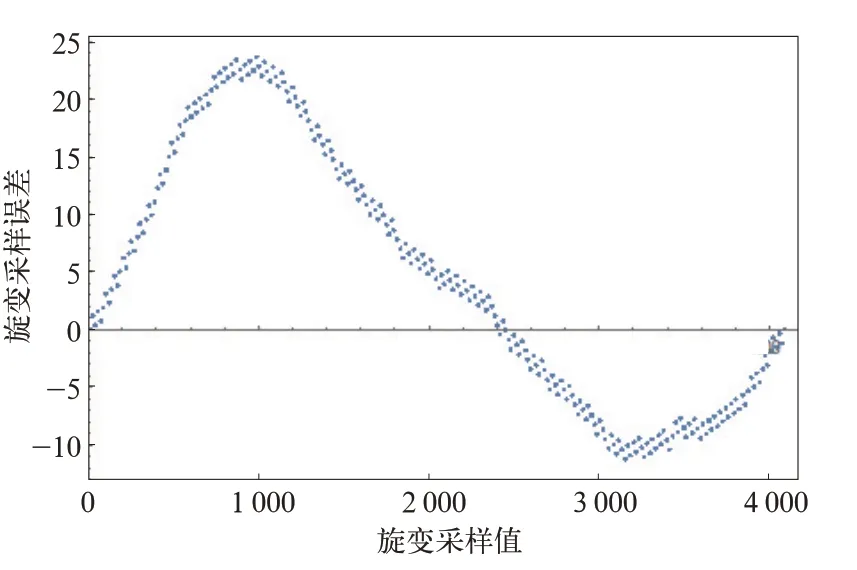
图3 误差分布曲线
转子位置角度误差会引起矢量变换时所使用的角度θ不准确,从而使park 变换的结果也出现波动。由于转子位置是周期变化的,这种误差也是周期性出现的[6]。
式(1)中,当θ角度叠加误差Δθ时,式(1)变化为式(2):
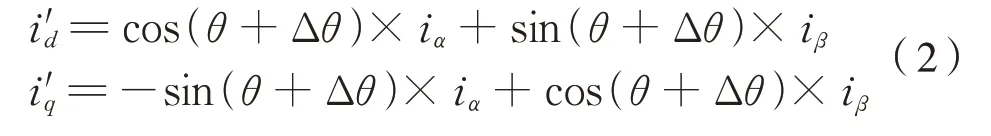
对引入误差Δθ后的park 变换表达式展开可得式(3):
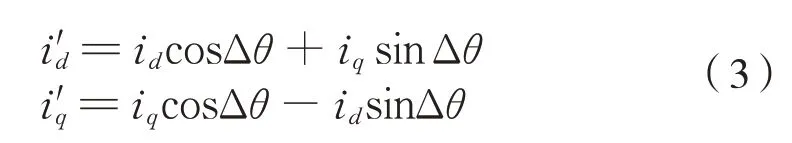
由式(3)可知,引入误差之后的d轴、q轴电流不仅与误差角度Δθ的余弦函数相关,还增加了与另一轴电流的耦合项。可见,一旦转子位置角度的采集引入误差,无论这种误差是线性变化或非线性变化,在进行坐标变换时,都会导致反馈电流id和iq叠加额外的扰动量,影响矢量控制的精度[7]。
某条件下转子位置角度无误差时的id和iq波形如图4 所示,叠加的误差呈正弦变化时,id和iq波形如图5 所示,叠加的误差呈恒定值变化时,id和iq波形如图6 所示。可以看出,当转子位置角度叠加一定误差后,d轴、q轴电流存在波动或偏执。在其他形式角度误差下,id和iq也会出现类似的波动或偏执,不再一一列举。

图4 理想id、iq

图5 叠加正弦误差的id、iq

图6 叠加直流偏执误差的id、iq
这种波动或偏执并非来源于负载电流的真实波动,如果控制系统根据带有这种波动的id和iq的反馈量进行调节,会导致逆变器的输出也会叠加此类波动,并最终传导至电机上,使电机的电流和转矩也出现波动,造成电机运行不稳定。因此,需要对这种误差进行抑制补偿[8]。
1.2 转子采集误差补偿
对转子位置角度误差的补偿,需要既考虑补偿的准确性又要考虑补偿方法在工程应用上的可实现性。一般是根据转子位置角度采集的误差分布曲线,对采集结果进行曲线拟合并反向补偿,以此抵消采集结果中叠加的误差,使补偿后的位置角度变化趋近于理想的直线[9]。
对于理想的旋转变压器,在一个周期内的所有采样点均落在同一条直线上。当旋转变压器自身存在如图3 所示的位置误差时,采样结果会分布在理想直线的两侧。由于位置角度变化的周期性,因此可以在采样结果的0(对应0°)和4 095(对应360°)2 个点或取最接近这2 个点的值(实际采样值在每个角度周期不一定刚好落在这2 个点上,取最接近的点即可)为起止参照点,并以此构建理想直线。
1.2.1 离线位置角度补偿
对转子位置角度可进行离线补偿。根据所采集的旋转变压器的结果,得到如图3 所示的误差曲线,采用数据处理软件对误差曲线进行分析,把所采集的误差数据导入软件中,使用软件中的数学工具进行分析拟合,得到误差曲线的表达式。
针对图3 中的误差分布曲线进行离线拟合的曲线结果为式(4):
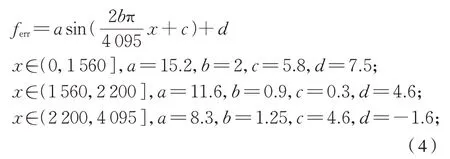
式中:x为转子位置角度采样点;a、b、c、d分别为拟合曲线系数。
把误差曲线的表达式作为补偿项对采集到的转子位置角度进行补偿,就可以得到消除误差后较为准确的电机位置角度数值。拟合曲线与误差分布的对应关系如图7 所示。可见拟合的曲线与误差分布曲线较为贴近。
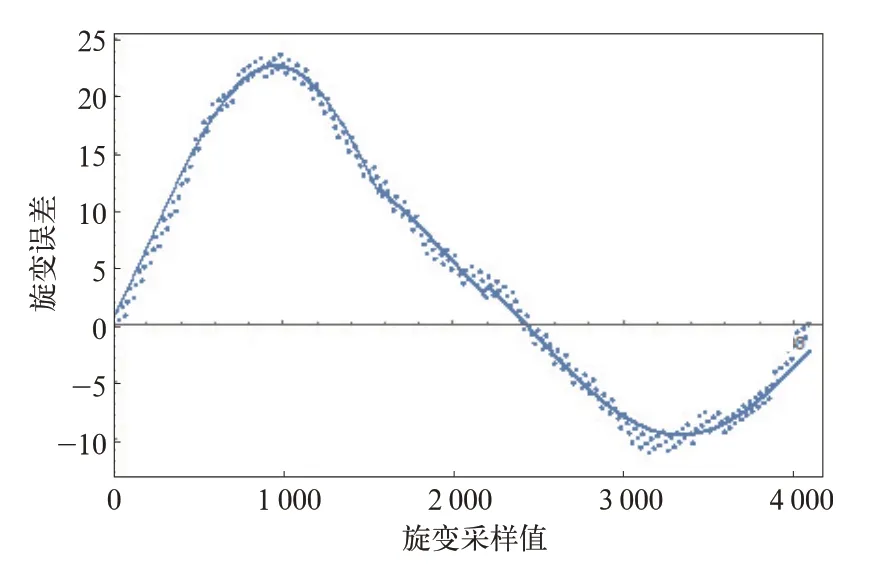
图7 拟合后的转子误差补偿曲线(实线)
1.2.2 实时位置角度补偿
采用离线补偿拟合的方式,虽然能够针对转子位置角度的误差分布得到较为贴近的误差曲线表达式,但是在实际的工程项目中,由于电机数量较多,且每台电机的误差特性分布也不完全相同,如果对每台电机单独测量校正,工作量很大,难以满足工程应用要求。因此须考虑对旋转变压器的误差进行自动辨识校正。
自动辨识校正方式须同时满足准确性和易实现性。转子位置角度误差曲线是非线性且不规则曲线,由于电机控制器内部硬件资源和运算能力的限制,无法采用类似于离线拟合所使用的复杂数学函数在软件中对其进行在线实时拟合,因此直接对转子位置角度误差进行拟合较为困难。
为保证拟合精度和软件运算速度,这里采用中点均值补偿法。中点均值补偿把采集到的离散转子位置角度分为若干个误差运算的区间,每个区间为一小段直线,由此转子位置角度曲线被划分成由多条直线段组成的线段组合,对每一个区间单独计算误差补偿量。
中点均值补偿法首先需要构建理想的转子位置采集曲线。由前文所述,理想曲线采用每个0°~360°周期内首尾2 个点构建,其结果是一条直线。
在运算的过程中,首先采集记录一个0°~360°周期内位置角度采集点的数据和采集时间。从第1 个采集点开始,依次把每2 个相邻的采集点作为1 个计算区间。理想位置角度曲线和实际采集位置角度的关系如图8 所示。
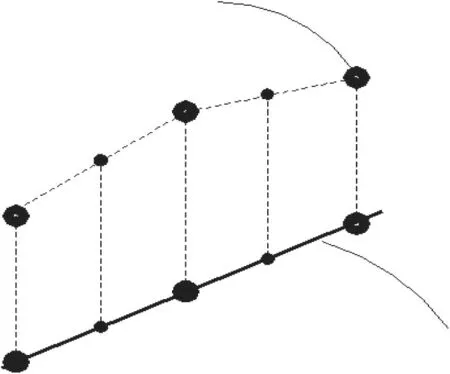
图8 理想位置曲线和实际采集位置角度的关系
在任意2 个采样值之间,取其中点值作为这一区间内所采集位置角度的平均值为式(5):
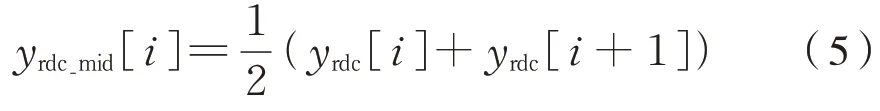
同时计算对应的理想位置曲线的中点值为式(6):
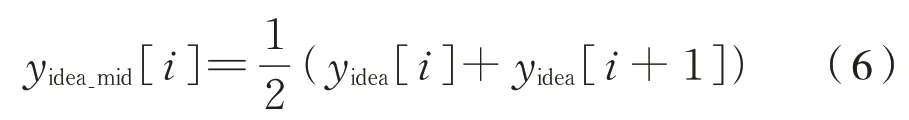
计算yrdc_mid[i]和yidea_mid[i]这2 个点的差值,从而获得这一区间近似的误差为式(7):

从而得到式(8):
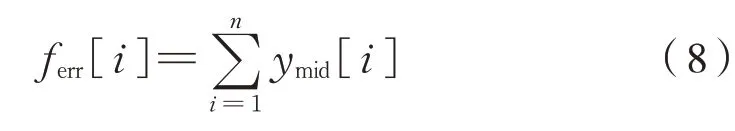
这个差值数组可以作为当所采集的转子位置角度值处在yrdc[i]和yrdc[i+1]之间的误差平均值。当采样值处于此区间内,都可以使用采集的转子位置数值减去此差值,从而得到趋近于理想值的转子位置角度值。
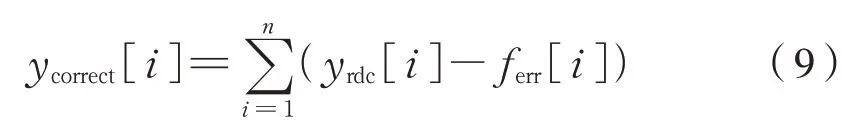
在应用时,受到控制器采样频率限制,可以在电机处于低速运行时完成中点均值计算。因为电机低速运行时频率较低,因此采样点较多,能够划分出的线段区间也较多。每2 次采样值之间的增量较小,因此所计算的中点均值的分布特性可以认为比较接近所采集的位置角度采样值的分布特性。而且在电机低速运行时只需计算1 次,把计算结果放入控制器内部的寄存器中,后续采样时就可以按照转子位置角度采样数值自动判断其所在的区间并自行补偿计算,运算简单,不会降低软件执行效率。
对此方法的仿真的结果如图9 所示。在仿真时构建了带有正弦变化的转子位置角度采集曲线(为便于观测,仿真时设定所叠加的误差要比实际转子位置采集误差大4 倍左右),可以看出,该方法对转子位置角度的误差跟踪较为准确。
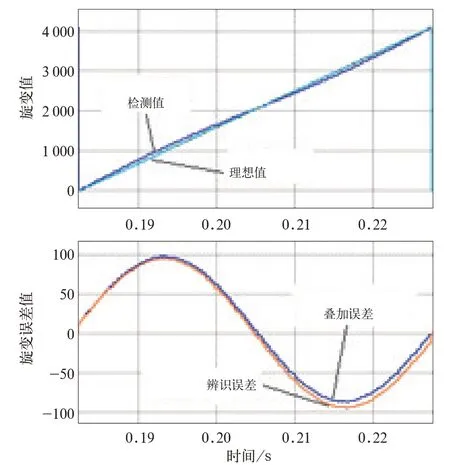
图9 中点值误差计算仿真结果
2 试 验
依托某有轨电车项目,搭建试验平台如图10 所示,对此方法进行验证。牵引电机额定功率130 kW,额定频率120 Hz,额定电压450 V,额定电流183 A,额定转矩690 N⋅m,极对数为4,Ld=0.82 mH,Lq=1.67 mH。牵引逆变器额定电压750 V,额定功率150 kW,最大电流360 A。

图10 电机控制试验台
电机在3 000 转和3 500 转下,未进行转子位置角度补偿校正时的电流波形分别如图11、图12 所示,可见电机电流存在较大的波动。
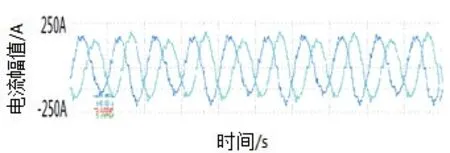
图11 3 000 转下,补偿前给定满转矩时U、V 相电流波形
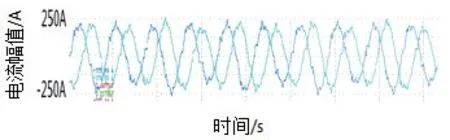
图12 3 500 转下,补偿前给定满转矩时U、V 相电流波形
电机在3 000 转和3 500 转下,采用中点均值补偿法对转子位置进行补偿校正的电流波形分别如图13、图14 所示,在消除了转子位置采集过程中所叠加的误差后,电机电流再无波动,电机运行稳定。
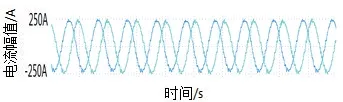
图13 3 000 转下,补偿后给定满转矩时U、V 相电流波形
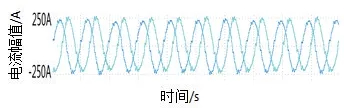
图14 3 500 转下,补偿后给定满转矩时U、V 相电流波形
3 结 论
仿真和试验表明,文中采用的基于中点均值分段校正的转子位置误差补偿方法,可以有效地对采集到的转子位置角度误差进行校正,校正后转子位置角度误差减小,有效地减小了在电机控制过程中转子位置角度误差引起的电流波动,提升了电机运行的稳定性,实现方式简单,无需大量复杂运算,符合轨道车辆应用要求,适用范围广泛。
