基于谱函数二阶导数的波达方向估计

潘秋甫 孙 曼 余小玲

(四川大学电气工程学院 四川 成都 610065)

0 引 言

DOA(信号波达方向估计)是信号处理领域的重要研究方向[1-2]，尤其是在短波测向[3]、军事对抗、雷达探测、声呐和移动通信等方面都有着广泛的应用[4]。随着电子战对作战隐蔽性及作战精密度要求逐渐增强，雷达等主动测向技术因主动发射电磁波进行测向，容易被捕捉信源方向，大大降低了作战安全性，因此高精度高分辨率的被动测向技术成为军事测向的发展趋势[5]。

基于多重信号分类的高分辨空间谱测向算法克服了传统比幅比相式测向机制[6]的缺点，可对同信道中多个信号进行超分辨测向，实现波束合成[7]和同频干扰检测，以其卓越的测向性能得到了广泛的关注和研究。文献[8-10]通过降低MUSIC算法的计算复杂度来达到较好的工程实用价值。然而，这类算法对计算量降低效果有限，且是以降低计算精度为前提的。文献[11-13]提出将现代信号处理方法作用于空间谱估计，使得信号处理技术在空间谱估计中有了新的发展。文献[14-15]采用特殊阵列模型结构，一定程度提高了低快拍数条件下算法的估计性能。文献[16-17]通过改善信号和噪声的正交性，来提高算法在低信噪比、小快拍数等复杂环境下的分辨率。然而，当信源角度接近时DOA估计精度将会受到影响。

本文针对低信噪比、小快拍数或信源角度相近等复杂环境下DOA估计性能严重下降这一问题，利用MUSIC空间谱函数的二阶导数能在原始波达方向周围产生负峰值的特性，通过对二阶导数空间谱进行负峰值搜索实现DOA估计。相比常规DOA估计算法，本文方法在不严重增加运算量和计算复杂度的基础上，大幅度地提高了复杂环境中DOA估计的测向精度，有较强的工程实用价值。

1 信号模型

假设N个窄带远场信号源si(t)以角度θi(i=1,2,…,N)入射至空间某均匀线型阵列上，其中阵列天线由M个线性分布阵元组成，假设阵列中各阵元是各向同性的且不存在通道不一致、互耦等因素的影响。假设噪声为零均值、方差为δ2的高斯白噪声，阵元间噪声彼此独立，且与信号不相关。以最左侧阵元为参考阵元，则其阵列接收信号写成向量表达式为：

X(t)=A(θ)S(t)+N(t)

(1)

式中：X(t)为阵列接收的快拍数据的向量表达式；A(θ)为对应的M×N维阵列流形矩阵；N(t)为噪声向量。其中:

X(t)=[x1(t),x2(t),…,xM-1(t),xM(t)]T

(2)

A(θ)=[a(θ1),a(θ2),…,a(θM)]

(3)

(4)

S(t)=[s1(t),s2(t),…,sM(t)]T

(5)

N(t)=[n1(t),n2(t),…,nM(t)]T

(6)

R=E[X(t)XH(t)]

(7)

式中：E为期望值；R为信号协方差矩阵。

2 MUSIC算法简介

对协反差矩阵进行特征分解可得：

(8)

式中：US为大特征值对应的特征向量所组成的信号子空间；Σ为由特征值组成的对角矩阵；UN为小特征值对应的特征向量所组成的噪声子空间。在理想情况下，数据空间中的信号子空间与噪声子空间相互正交，即信号子空间中的导向向量也与噪声子空间正交，则式(9)成立。

aH(θ)UN=0

(9)

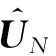
(10)

所以，MUSIC算法的谱估计公式为：

(11)

3 改进算法研究

文献[18]定义当存在某θc满足θc=1/2(θ1+θ2)且P(θc)=1/2[P(θ1)+P(θ2)]时，两信号能刚好被分辨出来，此时称Δ=|θ1-θ2|为MUSIC算法的分辨率。分辨率与采样快拍数L和阵元数目M均有联系。Kaveh等[19]定向分析出这几个变量与角分辨率的关系：

(12)

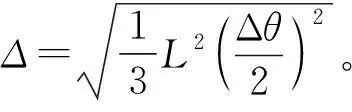
假设某均匀线阵阵元数为9，2个窄带远场信号s1(t)、s2(t)(信源之间相互独立)入射至该阵列，两信源的入射角度分别为θ1=0°、θ2=5°，两信源的信噪比分别为SNR1=4 dB、SNR2=4 dB，空间噪声为高斯白噪声。图1为使用传统子空间算法进行DOA估计所得空间谱P(θ)。

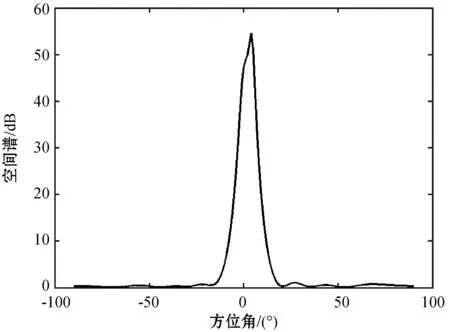
图1 MUSIC算法空间谱

可以看出，当信源角度接近时，并不会在0°和5°附近分别出现波峰，随着信源角度间隔减小，两谱峰将逐渐靠拢，慢慢融合为一，只会在θ=5°附近出现一个峰值，且谱峰不再明显，我们将不能通过谱峰搜索来确定信号的DOA信息，测向精度降低。

观察谱峰发现，谱峰附近左侧为增函数，即一阶导数大于零；右侧为减函数，即一阶导数小于零。仅依靠函数斜率的正负性的变化里确定极大值点是不够的，因为在极小值点的附近也会出现一些局部的波动，导致斜率的正负性变动，故函数的极值点一般是通过一阶导数和二阶导数来确定。对于一元可微函数f(x)，其驻点为x0，且f″(x0)<0，则f(x)在x0处取得极大值。仔细观察图1，可以发现在0°和5°之间会出现一段下凹的曲线，考虑对频谱求二阶导数，通过搜索二阶导函数的最小值点来确定波达角。

为提高计算精度，可以考虑保留更多的项数，选择保留二阶项，则连续函数二阶导数可近似简化为：

(13)

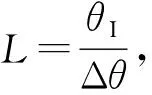
(14)

一维离散点P(θ)代入式(13)，当1≤i≤L-2时，近似求二阶导数值，可得：

(15)

基于谱函数二阶导数的DOA估计方法步骤如下：

3) 根据式(11)得到MUSIC算法估计的谱函数P(θ)。

4) 根据式(15)得到谱函数的近似二阶导数函数P″(θ)。

5) 对P″(θ)进行负向谱峰搜索，得到极小值点对应的角度即为波达角方向。

4 仿真结果分析

为验证本文算法的性能，分别将算法与经典DOA估计算法进行比较。为验证算法的有效性和估计性能，分别进行了三组仿真对比实验。

实验一验证本文算法的估计性能，考虑均匀线阵的阵元数为9，阵元间距为半波长。为实验方便起见，两入射信源s1(t)、s2(t)相互独立，两信号源的信噪比分别为SNR1=0 dB、SNR2=0 dB，阵列采样快拍数为200。图2和图3是两信源入射角θ1=0°、θ2=20°时，分别使用传统MUSIC算法和基于谱函数二阶导数DOA估计所得空间谱。图4和图5是两信源入射角θ1=0°、θ2=5°时，分别使用传统MUSIC算法和基于谱函数二阶导数DOA估计所得空间谱。

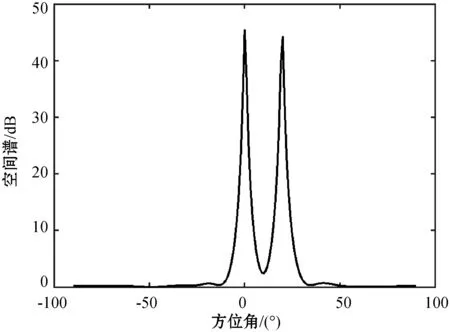
图2 θ1=0°、θ2=20°时MUSIC空间谱

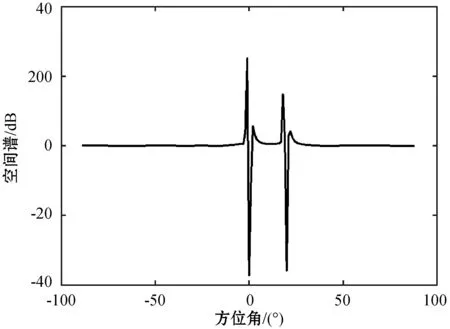
图3 θ1=0°、θ2=20°时二阶导数空间谱

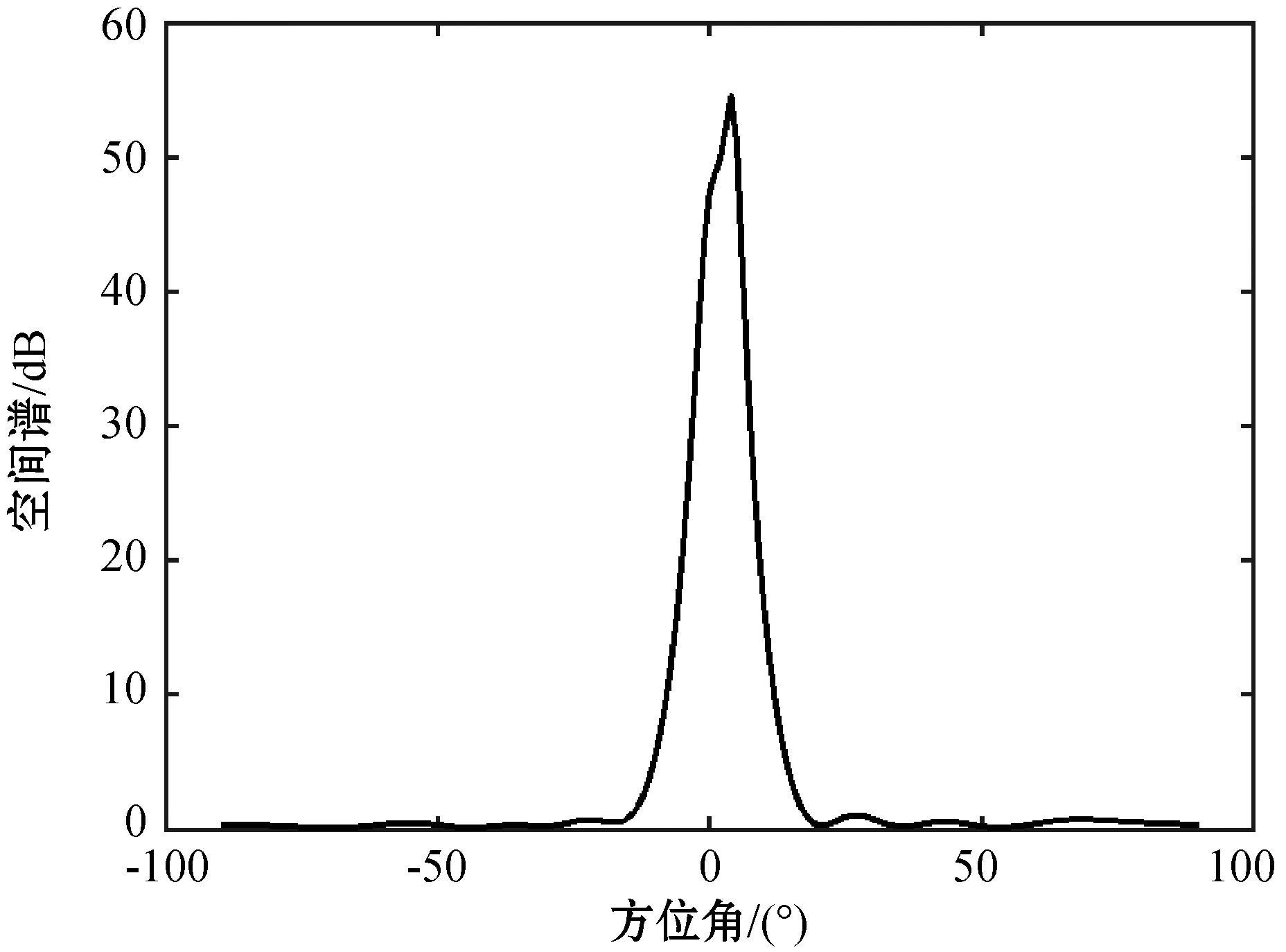
图4 θ1=0°、θ2=5°时MUSIC空间谱

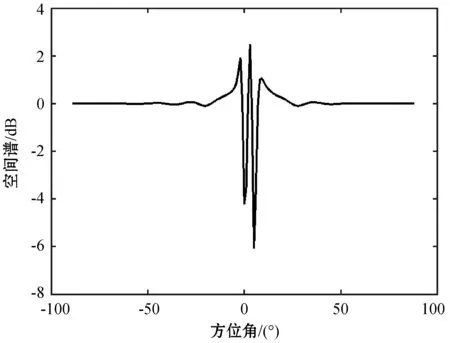
图5 θ1=0°、θ2=5°时二阶导数空间谱

当信源角度间隔较大时，如图2和图3所示，两种算法所得空间谱均会出现尖锐的谱峰，可以精确估计信源的DOA信息。两者的不同之处就是：传统MUSIC算法使用的是正向谱峰搜索，而基于谱函数二阶导数的DOA估计是利用大值点附近谱函数的二阶导数能在原始波达方向周围产生负峰值的特性进行负向谱峰搜索。

当信源角度间隔较小时，如图4所示，传统MUSIC算法并不能得到两个尖锐的谱峰，只能在4°附近搜索到一个谱峰，DOA估计性能下降。如图5所示，即使在信源角度间隔较小时，基于谱函数二阶导数的DOA估计算法仍能够迅速捕捉谱曲线中下凹部分，利用求二阶导数形成负向谱峰，进行精确的DOA估计。由此可见：基于谱函数二阶导数的DOA估计算法有良好的估计性能。

实验二验证本文算法对信噪比的敏感程度。考虑均匀线阵的阵元数为9，阵元间距为半波长，两入射信源s1(t)、s2(t)相互独立，两信源入射角分为θ1=0°、θ2=5°，为避免快拍数对实验结果的影响，取快拍数为500，信源的信噪比取-2 dB～15 dB，步进为0.5 dB。Monte Carlo实验次数为1 000。

如图6所示，随着信噪比的逐渐提高，两种算法的均方根误差均将逐渐减小。本文算法的精确度显然高于传统MUSIC算法，即使在信噪比较低的情况下，如SNR=-2 dB，本文算法估计的均方根误差为0.95，而此时经典MUSIC算法的均方根误差接近为2；当信噪比达到9.5 dB及以上时，本文算法的均方根误差为0。

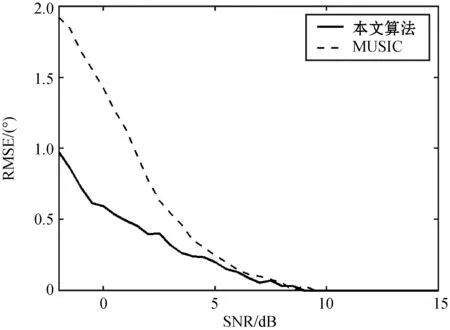
图6 算法对信噪比的敏感程度

实验三验证本文算法对快拍数的敏感程度。考虑均匀线阵的阵元数为9，阵元间距为半波长，两入射信源s1(t)、s2(t)相互独立，两信源入射角分为θ1=0°、θ2=5°，为避免信噪比对实验结果的影响，取信噪比为8 dB，信源的快拍数取20至800，步进为20。Monte Carlo实验次数为1 000。

如图7所示，随着快拍数的逐渐提高，两种算法的均方根误差均将逐渐减小。本文算法的精确度显然高于传统MUSIC算法，即使在快拍数较低的情况下，如快拍数为50时，算法估计的均方根误差为0.55，而此时经典MUSIC算法的均方根误差接近为1.3，是本文算法的两倍以上；当快拍数达到650及以上时，本文算法的均方根误差近似为0。

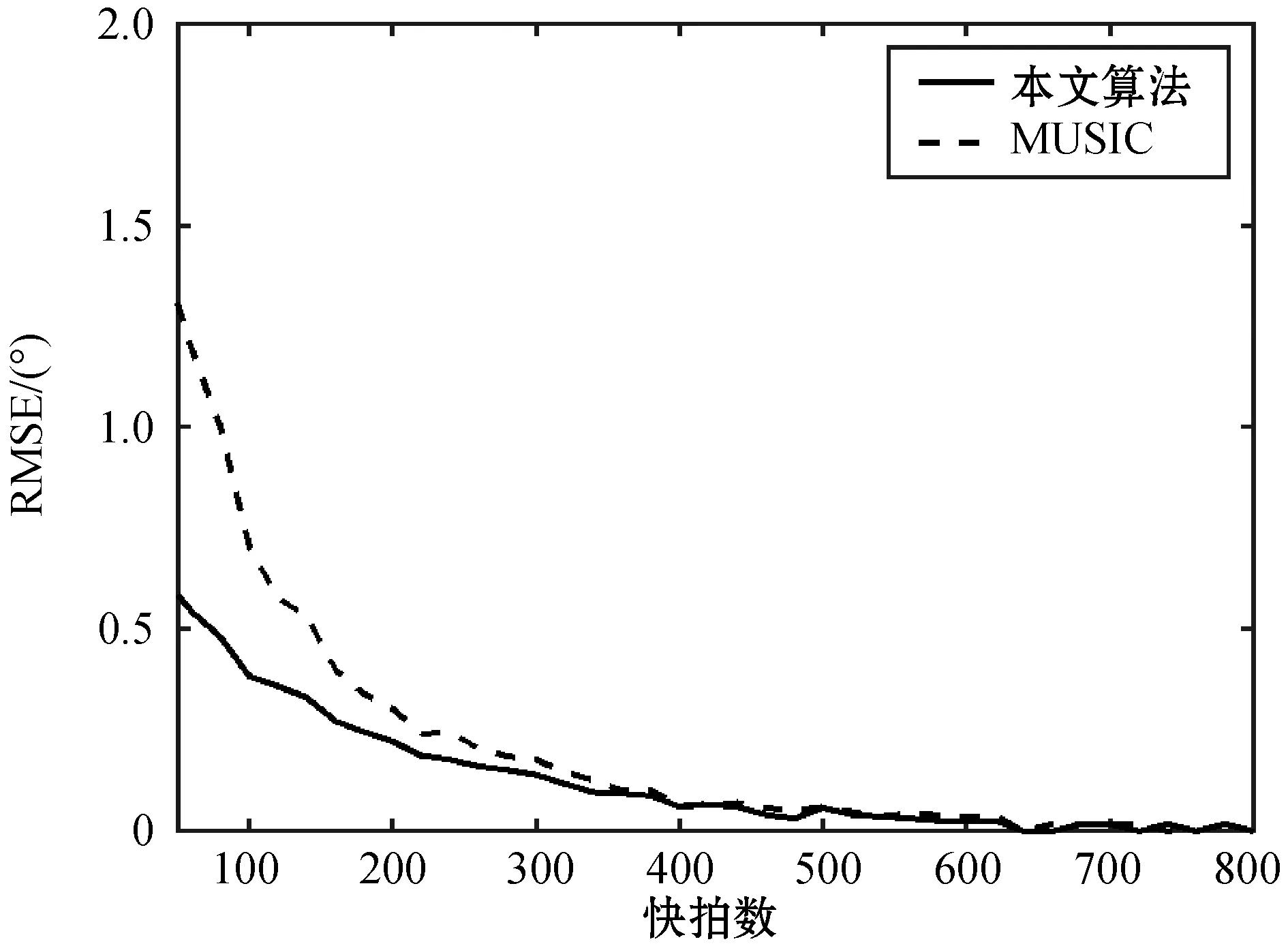
图7 算法对快拍数的敏感程度

5 结 语

经典算法受阵列元数、快拍数及信噪比门限的限制，在复杂环境下DOA估计分辨率将严重下降。本文利用MUSIC空间谱函数的二阶导数能在原始波达方向周围产生负峰值的特性，研究了基于谱函数二阶导数的波达方向估计方法，通过对二阶导数空间谱进行负峰值搜索实现DOA估计。仿真实验表明，相比常规DOA估计算法，本文方法在不严重增加运算量和计算复杂度的基础上，大幅度地提高了复杂环境中的DOA估计的测向精度，有较强的工程实用价值。