吸气-振荡射流激励器振荡特性

孙启翔，王万波，黄勇

中国空气动力研究与发展中心 低速空气动力研究所，绵阳 621000

振荡射流激励器没有任何运动部件，相比于其他主动流动控制(AFC)装置具有结构简单、鲁棒性强等优点，且射流振荡频率可以在10 Hz～20 kHz之间变化，因此其已应用到分离控制、腔体噪声抑制、燃烧控制等问题上。

振荡射流激励器可分为无反馈通道、单反馈通道和双反馈通道3种类型。无反馈通道激励器由两股入射流相互作用使射流发生振荡。有反馈通道激励器由射流入口、振荡室、反馈通道和射流出口组成，射流流入振荡室后科恩达效应会使其附着于振荡室的一侧壁面上，同时部分流体会流经反馈通道，并在出口处撞击射流，使其偏向另一侧，从而使射流振荡。

尽管振荡射流激励器在抑制翼型、机翼、垂尾和机翼-短舱组合体上的气流分离方面效果显著，但由于AFC系统需要从发动机引气，这会影响发动机性能。而飞机着陆时，发动机处于慢车状态，可供给AFC系统的空气量将大大减少，因此任何能减少其从发动机中引气的方法都值得进一步研究。已有的方法有：从高压气源和外环境同时引气以降低高压气源的负担；提高AFC系统的效率以减少用气量。

对于前者，Arwatz等将引射器与单反馈通道振荡器结合，设计出吸气-振荡射流激励器，其用少量高速气流引射外环境低速气流，两者流量之比可达1∶2，这大幅减少了引自高压气源的气体流量。在此基础上，Wilson等进行了基于吸气-振荡射流的卵状模型减阻研究。Kim等运用大涡模拟方法研究了某型吸气-振荡射流激励器的特性。Dolgopyat和Seifert将基于吸气-振荡射流的虚拟操纵系统应用到了IAI AR2翼型上。

对于后者，目前开展的研究主要集中在激励器入流参数、尺寸、出流特性和布置方式对流动控制效果的影响方面。Woszidlo和Wygnanski研究了吹气的动量系数和体积流量系数对増升效果的影响。Koklu等分别研究了激励器的出口尺寸和宽高比对分离控制效果的影响。Bauer等和Koklu分别研究了射流扫掠角和振荡频率的作用效果。还有学者研究了激励器在翼面上的弦向布置位置、展向布置方式、间距和角度对翼面气动特性的影响。

针对激励器本身的研究较少，多集中于定性描述其内流结构和分析几何参数对振荡频率的影响趋势方面。而对于高效的AFC系统，振荡特性优良的激励器必不可少。研究表明，越大，控制效果越好；振荡射流的控制效果优于定常吹气的原因是其沿流向产生了大小和涡强不断变化的非定常旋涡，促进了附面层内外掺混；射流扫掠角越大，达到相同控制效果所需的激励器数量就越少；尽管控制效果对射流振荡频率不敏感，但存在最优控制频率。因此，在入流条件一定时，应尽量减少激励器内部流动损失、避免射流在0°偏角处停滞过长时间、增大其扫掠角、并能够有效控制其振荡频率。

由于激励器几何形状复杂，难以对不同外形的激励器进行试验研究，而大多数CFD模拟是针对某一特定形状激励器的，所以目前尚无文献系统地给出激励器外形设计方法和减少内部流动损失、停滞时间以及增大射流扫掠角的方法。尽管现已有多种振荡频率模型，但在入流条件和几何参数影响频率的机理方面却鲜有研究。

本文以能够大幅减少引入高压气源气体流量的吸气-振荡射流激励器为研究对象，重点研究其单反馈通道振荡器的振荡特性，通过对不同几何外形的激励器进行数值模拟，总结出其外形设计方法和减小内部流动损失、停滞时间和增大射流扫掠角的优化方法，最终根据射流振荡机理建立该型激励器的振荡频率模型，说明了入流流速与几何外形影响振荡频率的原因。

1 模型与研究方法

1.1 基本模型与简化方法

如图1和图2所示，吸气-振荡射流激励器由引射器和单反馈通道振荡器两部分组成，振荡器的几何参数有：射流入口高度、反馈通道宽度、反馈通道整流段长度、反馈通道长度、圆角、喉道高度、扩张角、扩张段长度和出口高度，定义喉道以内为反馈段，=+为反馈段长度。

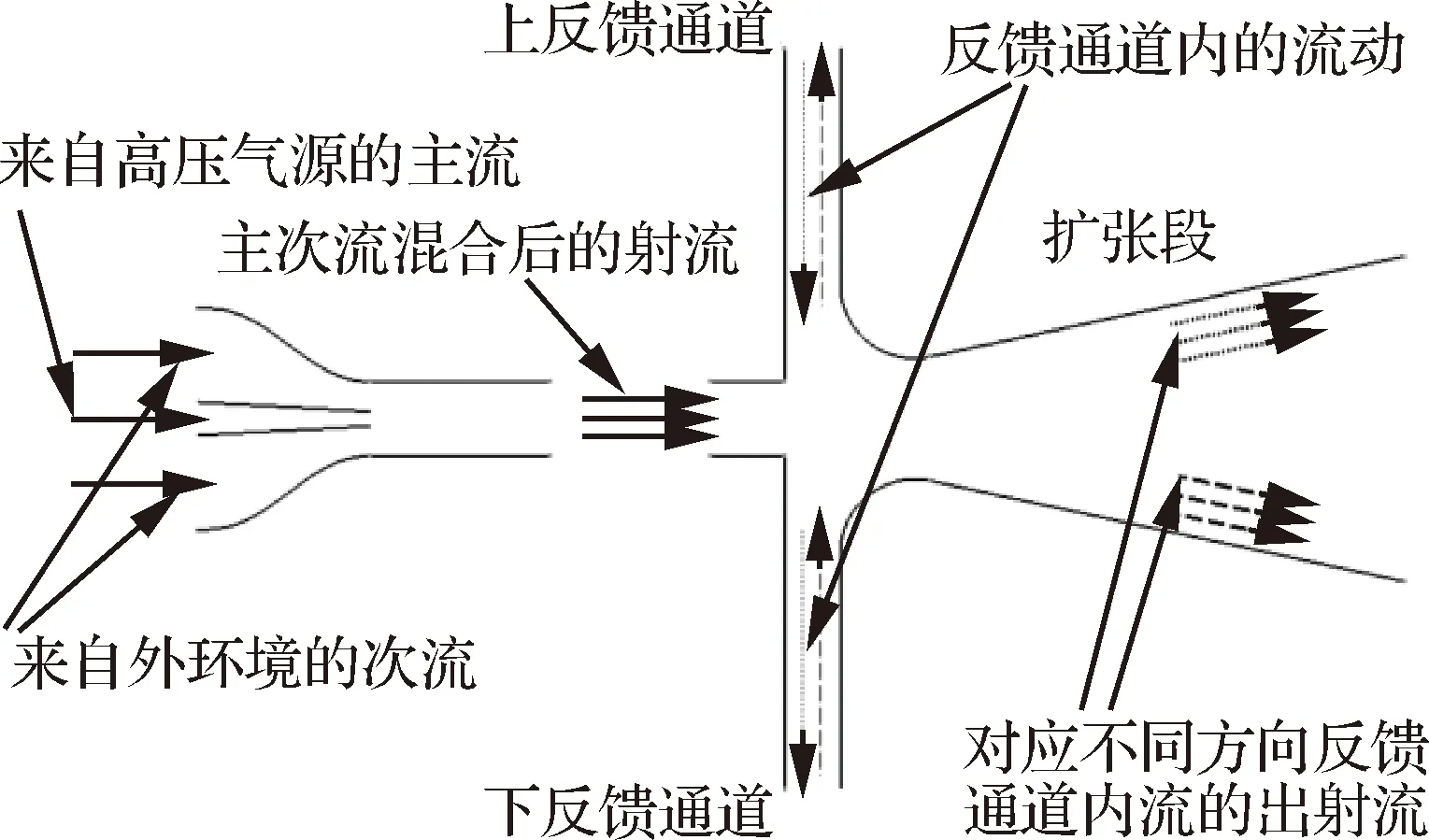
图1 吸气-振荡射流激励器示意图Fig.1 Schematic diagram of suction and oscillatory blowing actuator

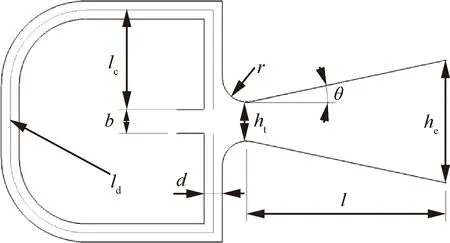
图2 振荡器主要几何参数Fig.2 Main geometric parameters of oscillator

由于在文献[30-31]中，经二维简化后激励器的数值模拟结果与试验数据吻合较好，因此本文将激励器内外流场简化为二维流场，基本模型R1是由文献[10]中的小尺寸激励器修改而成的二维模型。由于文献[10]中未研究对激励器振荡特性的影响，故本节将根据文献[10]中假设建立反馈段射流偏转轨迹模型以计算。如图3所示，文献[10]中忽略射流的扩散，假设其在入口处的速度为水平方向，使其偏转的向加速度在=0～之间为常值，其他地方为0 m/s，由上述假设可知，流体质点应在=0～之间做平抛运动，之后做匀速直线运动。由于当射流偏转至壁面时，应使得其刚好与扩张段壁面相切，则的计算式为

=(2+)tan+

(1)

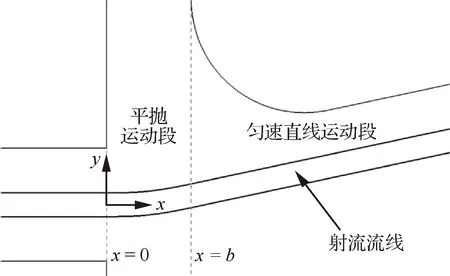
图3 射流轨迹示意图Fig.3 Schematic diagram of jet trajectory

图4给出了R1模型引射器的几何尺寸。本文控制值不变以保证入流雷诺数不变，并将振荡器长度尺寸化为关于的无量纲参数，则R1模型振荡器的几何尺寸可表示为=0.75、=4.5、=16、=1.0、=12°、=10，和可由其他几何参数推出。

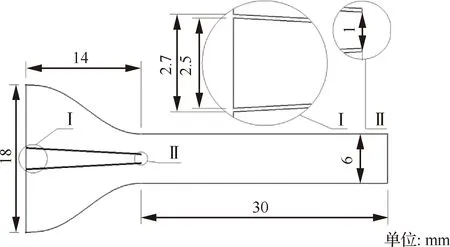
图4 R1模型引射器几何尺寸Fig.4 Geometric dimension of R1 model ejector

1.2 计算方法与边界条件

本文通过求解二维可压缩雷诺平均Navier-Stokes方程对流场进行非定常数值模拟，离散化方法为有限体积法，空间离散格式采用二阶精度迎风格式，时间推进方法采用LU-SGS(Lower-Upper Symmetric Gauss Seidel)隐式时间推进算法，采用SST(Shear Stress Transport)湍流模型进行计算。

本文所有计算网格均为多块结构网格，并在流场变化较剧烈的地方进行加密，物面法向第1层网格的无量纲高度=1，网格数约为10万，计算域采用边长为30的正方形计算域。激励器内部网格如图5所示，本文采用的坐标系如图3 所示，边界条件、监测点和监测线的设置如图6所示，其中监测点1和监测点2关于轴对称。

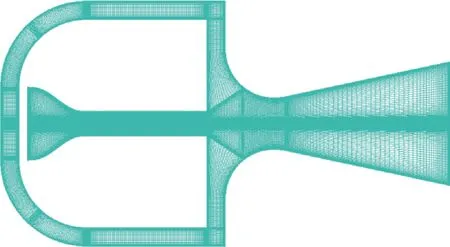
图5 R1模型内部网格Fig.5 Internal grids of R1 model

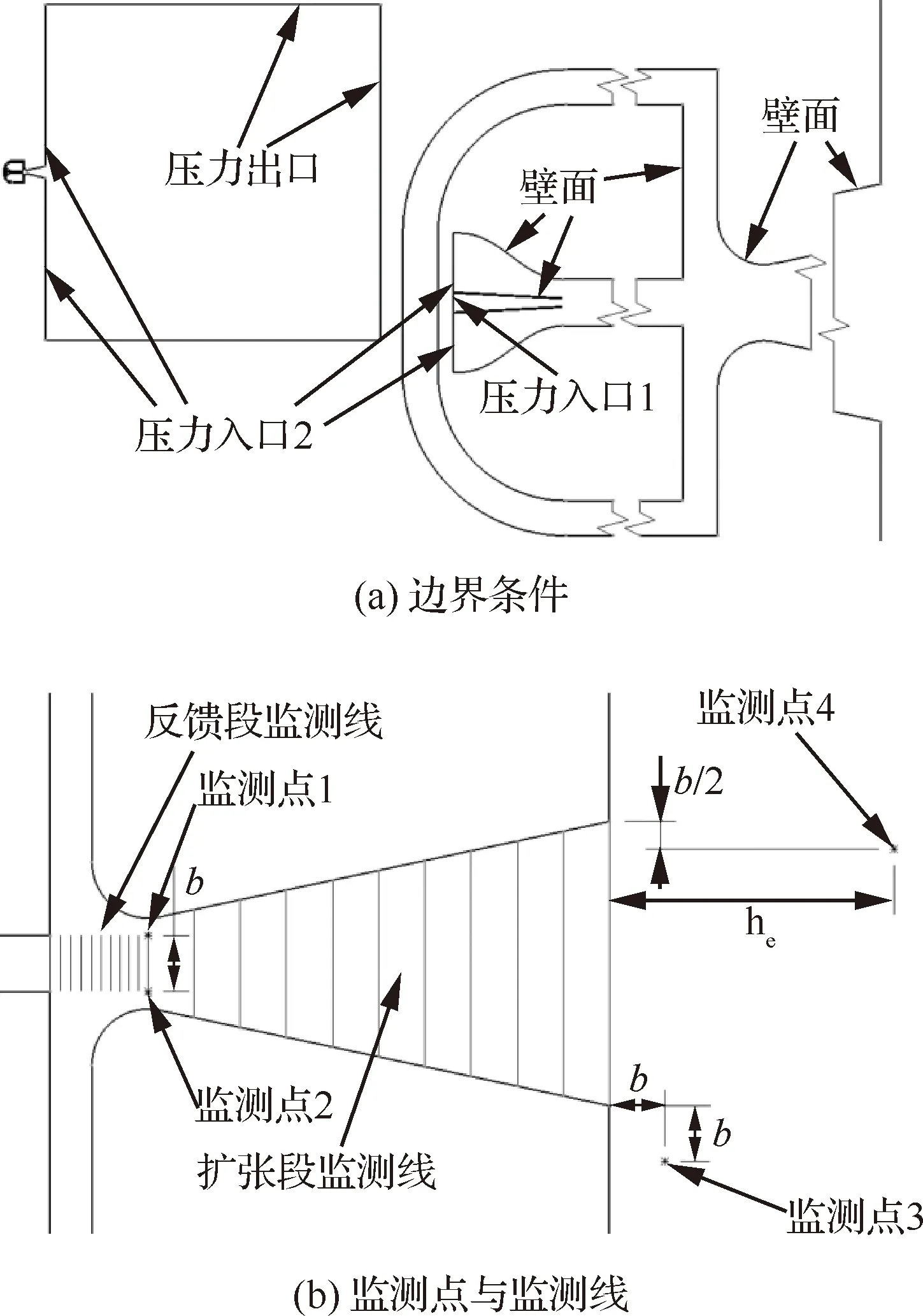
图6 边界条件与监视器设置Fig.6 Boundary conditions and monitor settings

远场和引射器次流入口处的大气参数取为海平面标准大气的值；在研究激励器几何特性时，引射器主流入口处的总压与远场静压之比取为1.5，此时射流入口处马赫数=0.4；非定常计算时间步长取1×10s；分析时仅提取流动时间在0.1 s以后的计算结果。

1.3 研究方法验证

为验证本文所采用的研究方法的合理性，现将文献[30]中的振荡射流激励器简化为二维模型，采用1.2节述方法对该验证模型进行数值模拟并与风洞试验结果对比。

对验证模型划分网格时，应保证其与R1模型网格有相同的值和计算域大小，在发生两股流体掺混和产生分离涡的区域，应保证两模型网格的节点分布状况相近。验证模型的几何外形与内部网格如图7所示。文献[32]通过风洞试验给出了射流出口流速与射流振荡频率的关系，以及=15 m/s，相位=0°,60°,120°,180°时的流场结构。为了验证网格密度对射流起振的影响，本文划分了粗、中等、较密、密4种网格，网格数分别为1万、2.5万、6万和12万，并给出验证模型监测点处流速随时间的变化(此时=15 m/s)。如图8(a)所示，较密和密网格的计算结果很接近，这说明此时计算结果与网格数无关，故本文将采用较密网格进行计算。和流场结构的试验结果与本文计算结果的对比如图8(b)、图8(c)所示，由图可知两者一致性较好，从而可以验证本文所采用的研究方法是合适的。

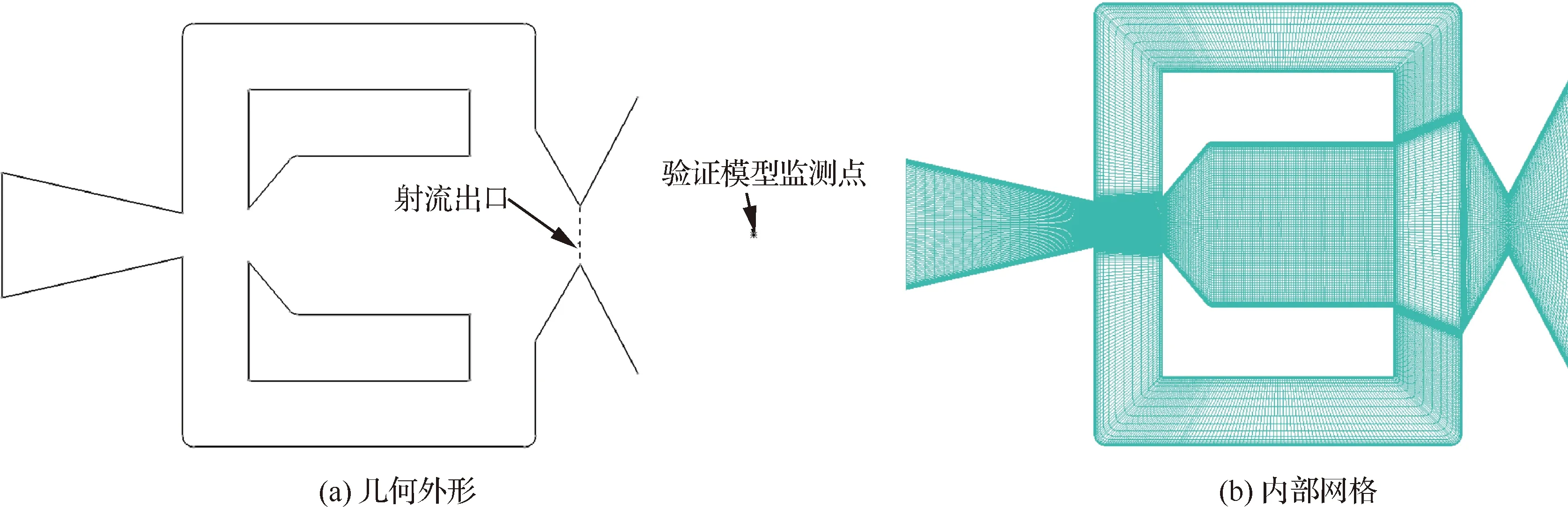
图7 验证模型的几何外形与内部网格Fig.7 Geometry and internal grids of validation model

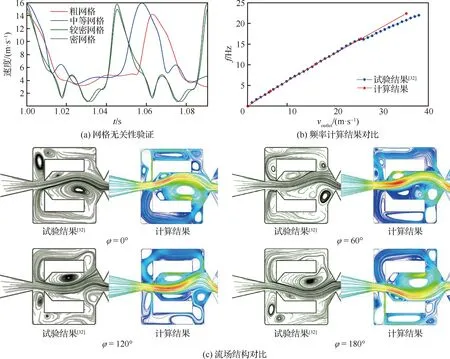
图8 研究方法验证Fig.8 Validation of research methods

2 几何参数对起振特性的影响

定义射流从轴位置起，首先上偏至上极限高度，再反向偏转至下极限高度，最终回到原位置的过程为一次振荡。则在一段时间内，若射流每完成一次振荡所需要的时间以及每一次振荡的极限高度值均不随流动时间而变化，则称射流稳定振荡。而在一个振荡周期内，若射流两次分别紧贴于扩张段上下壁面，则称射流完全偏转。只有当射流既稳定振荡，又完全偏转，才可以认为其起振成功。本节研究了能使射流起振成功的反馈段几何参数(、、)设计方法。

2.1 反馈通道宽度和圆角的影响

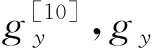
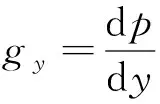
(2)

式中：为压力。

令射流内气体的平均密度为，则使射流偏转的向加速度j的表达式为

(3)

j指向的反向。本节以R1模型为基础，保持和不变并分别改变和，生成D组和R组激励器模型以研究两几何参数对反馈段分布的影响，本节所采用的激励器模型如表1所示。

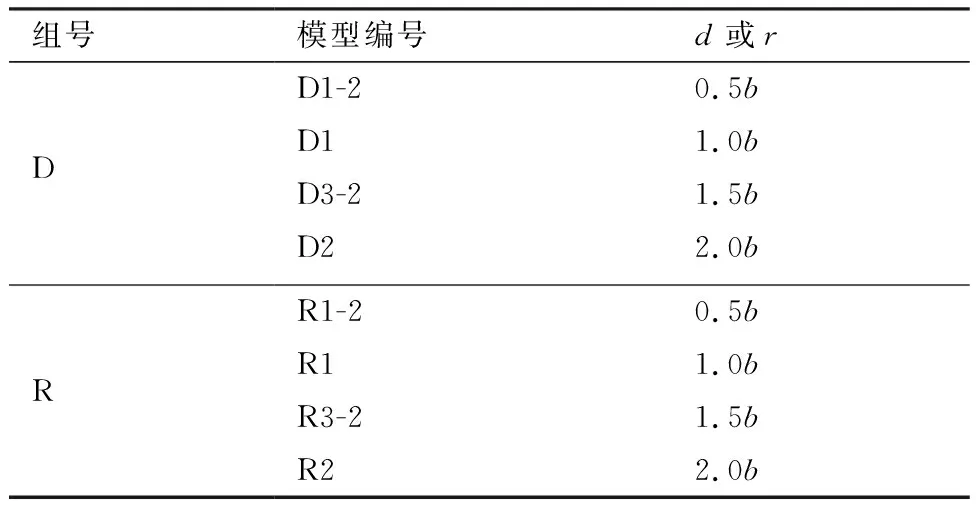
表1 D组和R组激励器模型Table 1 Group D and Group R actuator models

首先由监测点1和监测点2处速度随时间的变化(如图9和图10所示)确定射流偏转至极限高度时的时刻，再根据此时反馈段监测线上的速度型拟合出每一条监测线上的射流中心点(速度最大处)，将其连接为曲线即得此时反馈段内的射流中心线，最后对射流中心处的压力分布进行线性拟合以求出每一点的值，连成曲线即得压力梯度分布。

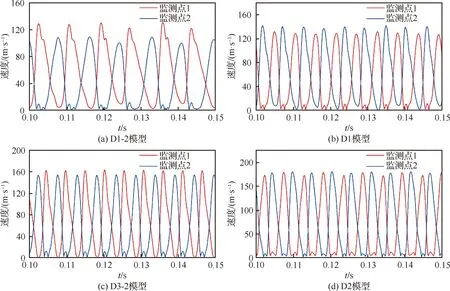
图9 D组模型监测点1和监测点2处速度随时间的变化Fig.9 Time variation of velocity at monitoring points 1 and 2 of Group D models

由图9和图10可知，在0.10～0.15 s内，能使射流振荡一次所需的时间和射流偏转极限高度值(由于射流的速度型并非匀布，因此当其偏移高度不同时，监测点处的速度也不同)为常数的激励器模型只有D3-2、R3-2和R2，即射流在此三者中稳定振荡。但由图9(c)所示，射流在D3-2模型中偏转到的上下极限高度不同(达到峰值时两监测点处速度不同)，而扩张段关于轴对称，故其一定未完全偏转。图11显示，射流在R3-2和R2模型中偏转到的上极限高度均接近壁面，因此可以认为射流在此二者中起振成功。

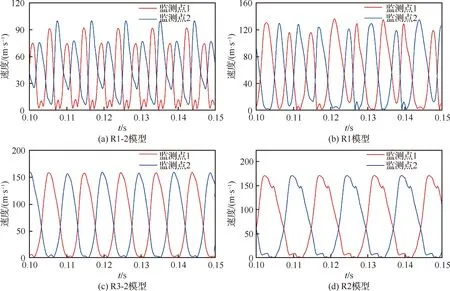
图10 R组模型监测点1和监测点2处速度随时间的变化Fig.10 Time variation of velocity at monitoring points 1 and 2 of Group R models

图11 T/4时R3-2和R2模型振荡器内的流场Fig.11 Flow field inside oscillator of R3-2 and R2 models at T/4

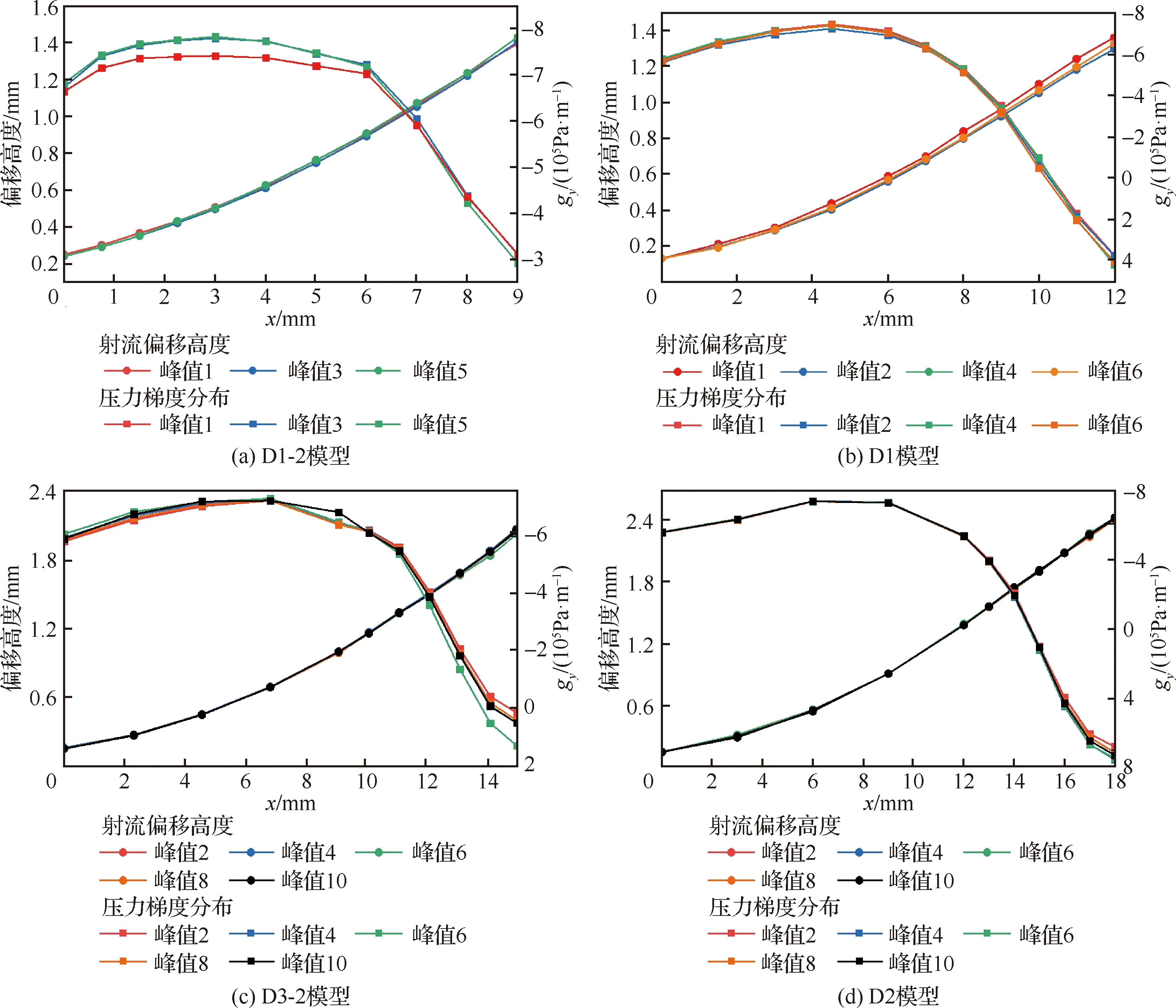
图12 D组模型反馈段射流中心线及gy分布Fig.12 Jet centerlines and gy distributions in feedback section of Group D models

接下来给出各模型反馈段中的射流中心线和其上的分布。为了方便研究，本文仅提取射流偏转至上极限高度(由监测点1所测)时的流场数据，为了验证数据的重合性，对每个模型的计算结果取多个峰值处的值，对于未使射流稳定振荡的模型，其由监测点1在不同时刻所测得的峰值速度各不相同，因此仅提取部分峰值速度较大时刻的流场数据。

取样峰值编号、射流中心线及其上分布的计算结果如图12和图13所示。由图可知，不同模型中射流中心处-的最大、最小值和分布趋势几乎不受和变化的影响。其最大值均在7×10Pa·m左右；而最小值则在(-8～3)×10Pa·m之间做无序波动；其分布的变化趋势相同，一开始-很大，变化较平缓，经过转折区域之后则近乎线性地急剧衰减。

接下来研究和对-分布中转折区域位置的影响，令′=/，分别对两组按以下方式进行归一化：

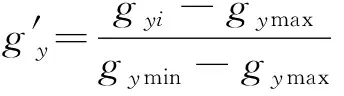
(4)

式中：为要进行归一化的值；max和min分别为每组中的最大、最小值。

由于式(3)表明j由决定，为了方便研究反馈段射流偏转轨迹，此处按以下表达式对归一化结果进行最小二乘拟合：

(5)

式中：av和为拟合参数。

计算结果如图14所示，由图可知不同模型的′分布重合性良好，这表明转折区域的位置不受和变化的影响。用式(5)可以较好地拟合′分布的平缓段和急剧衰减段，两拟合曲线的值分别为0.640和0.614，结果十分接近，因此可以认为转折区域近似位于0.6，与和无关。

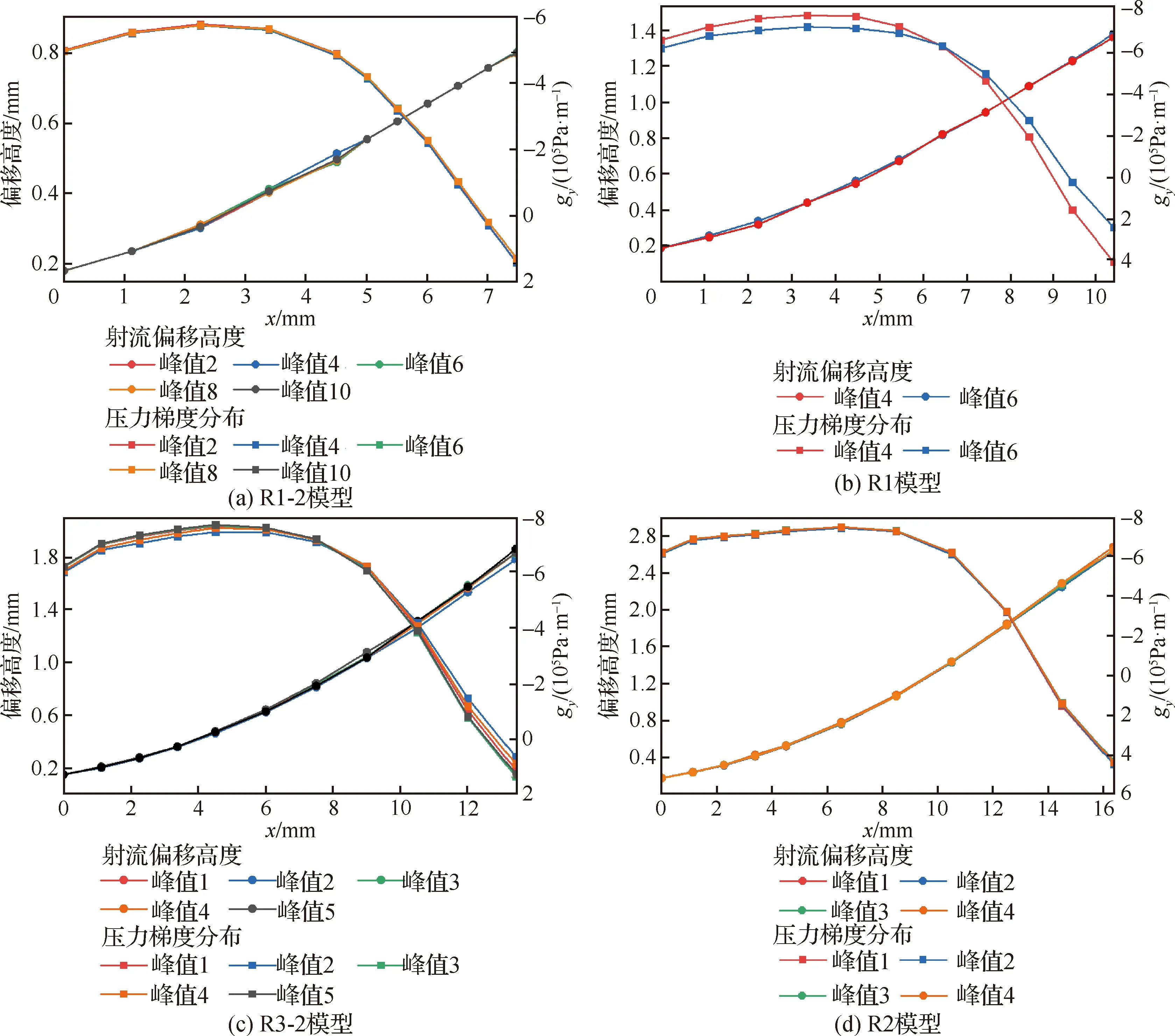
图13 R组模型反馈段射流中心线及gy分布Fig.13 Jet centerlines and gy distributions in feedback section of Group R models

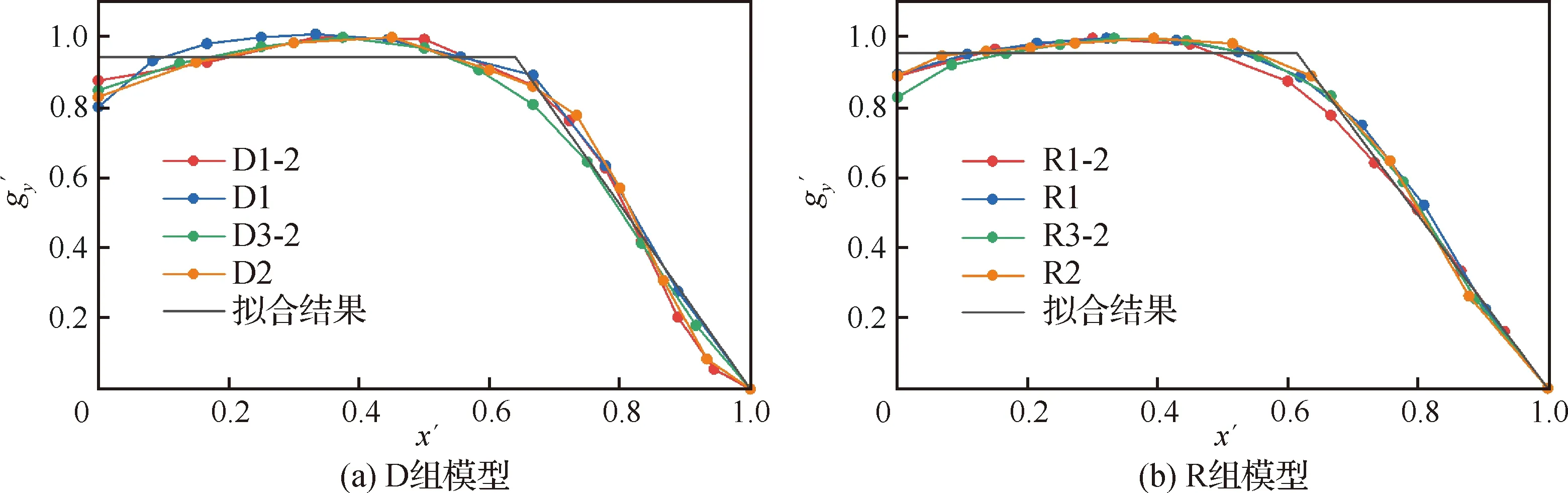
图14 gy的归一化与拟合结果Fig.14 Normalization and fitting results of gy

由于各模型-的最小值变化范围较大，故接下来将研究转折点之后的急剧衰减段对射流偏移高度的影响。由式(3)可知，j与-分布形式相同，现将图14所示的拟合曲线转化为加速度随的变化曲线，令直线段的加速度值为，流体质点通过反馈段所需的时间为，并对转化后的曲线进行左右矩形近似，结果如图15所示。

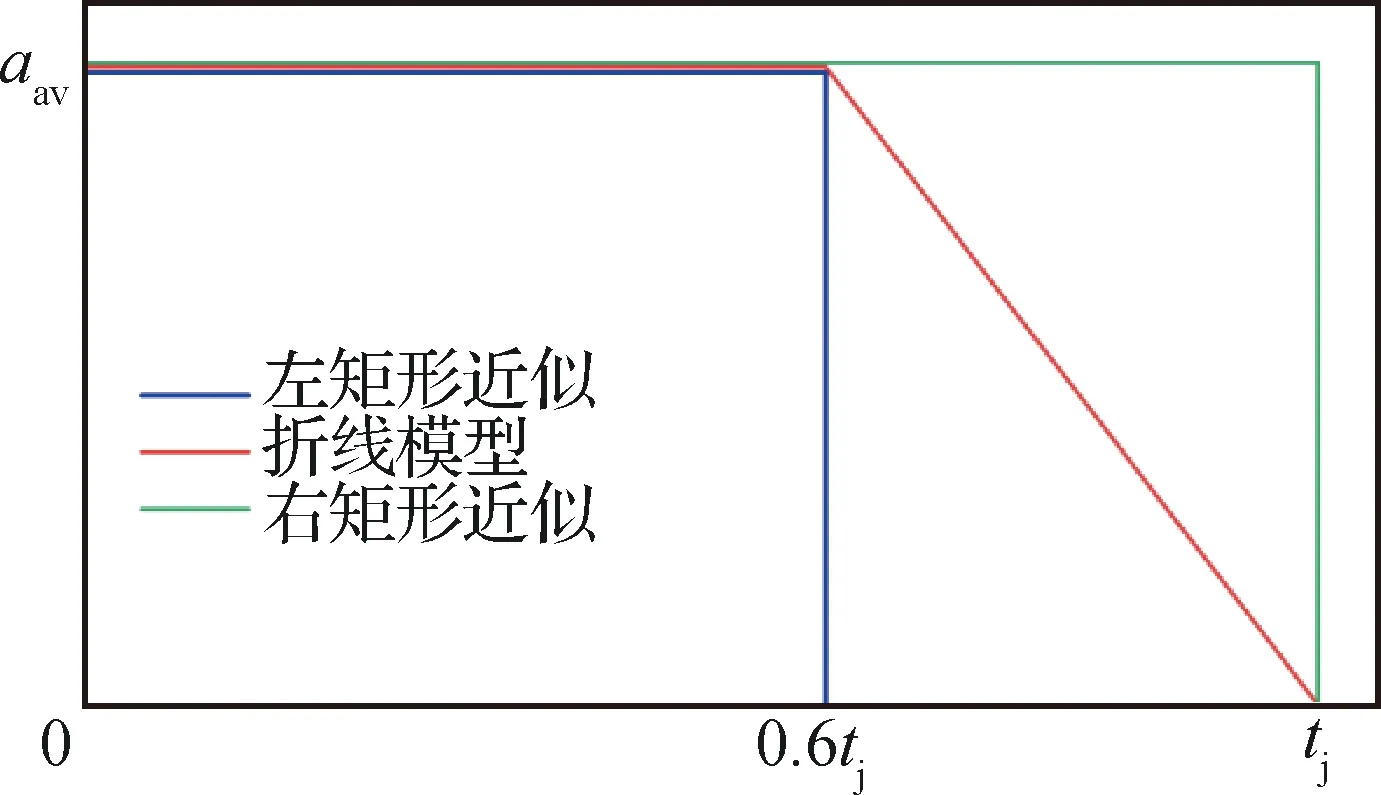
图15 加速度随时间的变化及其近似结果示意图Fig.15 Schematic diagram of time variation of acceleration and its approximate results

假设流体质点在反馈段入口处的速度方向为水平方向，则可以求得进行左右矩形近似后，流体质点的偏移高度增量之比为0.84，两者相差较小，故可以认为分布曲线中转折点之后的部分对射流偏移高度影响不大。综上所述，和只决定了的作用距离，因此当射流未完全偏转时，可以通过增加来延长的作用距离。由于实际上在=0～上均有分布，这与文献[10]中假设的仅在=0～上分布有出入，因此接下来将重新建立反馈段射流偏转轨迹模型。

2.2 反馈段射流偏转轨迹模型建立

为了使射流能够更易贴附于扩张段上下壁面，反馈段几何外形应使得射流在经过喉道后刚好与扩张段壁面相切，故本节将讨论反馈段射流偏转轨迹的函数形式。为了方便研究，采用图15中的右矩形近似，即用二次曲线拟合反馈段射流偏转轨迹。

拟合结果如图16所示。由图可知，射流轨迹在反馈段入口处的偏移和转角均不为0，这说明其起偏位置应在引射器内。由于射流刚起偏时的偏移高度和转角应为0，而又已知，因此只需根据图12和图13中的数据拟合出射流的等效起偏位置,即可由以上3个约束条件唯一确定一条二次曲线。等效起偏位置即是二次拟合曲线的顶点所对应的位置。

图16 二次曲线拟合结果Fig.16 Second curve fitting results

现对射流的等效起偏位置进行拟合，拟合函数为

=(-)+

(6)

式中：为拟合参数；和即为等效起偏位置和该处的射流偏移高度。

各参数的拟合结果如表2所示，由表可知接近于0，基本符合约束条件。随的变化如图17所示，其基本在4～7之间，本文取=。则与的关系为

=(+)tan+

(7)

后文中激励器模型的反馈段均按式(7)设计。

表2 各参数拟合结果Table 2 Fitting results of each parameter

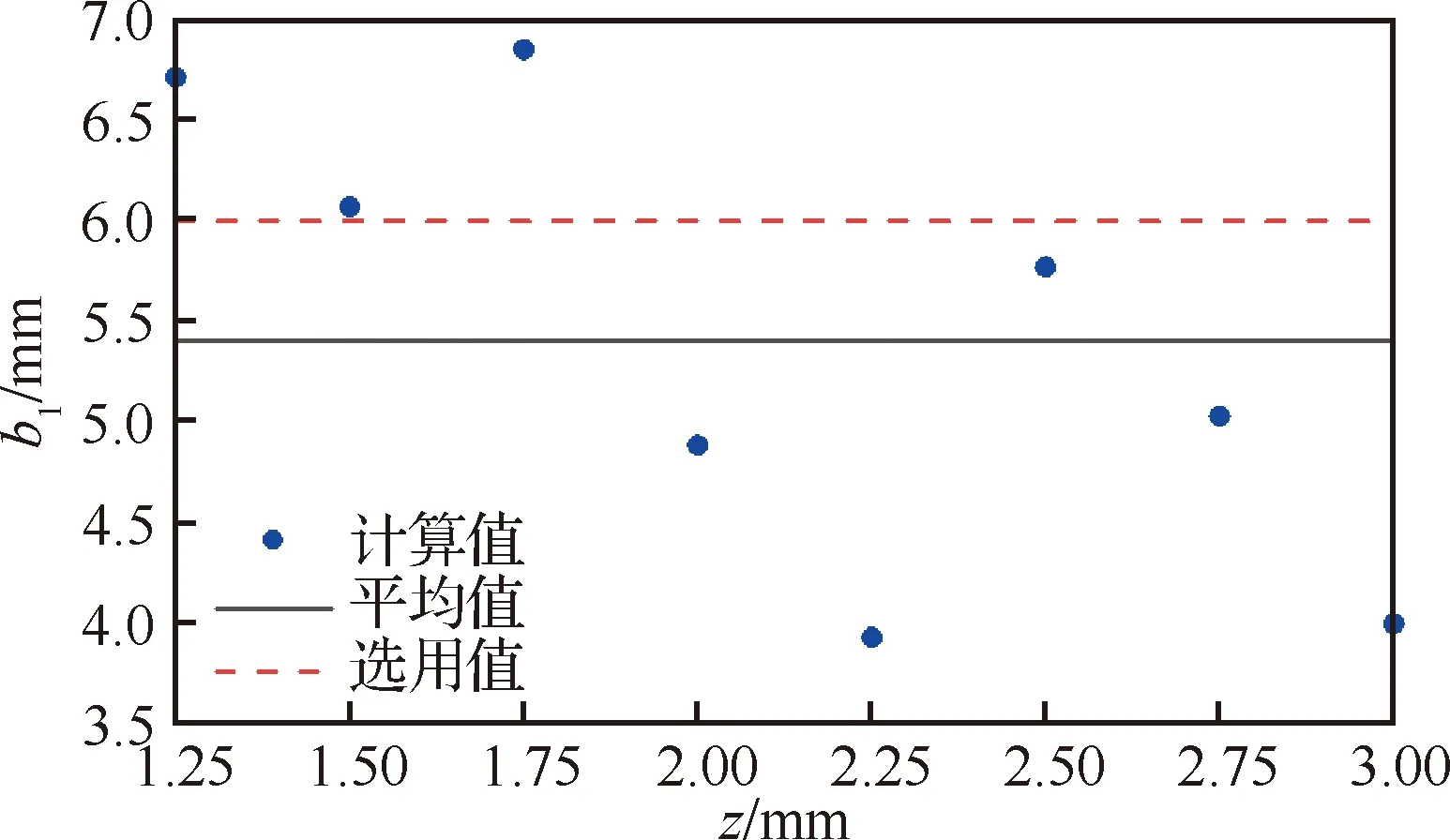
图17 b1随z的变化Fig.17 Variation of b1 with z

2.3 喉道高度的影响

本节首先对2.2节中建立的模型进行检验，取=2.4以保证射流能够在模型中完全偏转。改变与的比例，生成的Z组激励器模型如表3所示。计算结果如图18所示。

表3 Z组激励器模型Table 3 Group Z actuator models

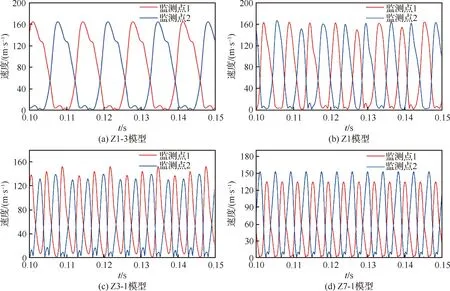
图18 Z组模型监测点1和监测点2处的速度随时间的变化Fig.18 Time variation of velocity at monitoring points 1 and 2 of Group Z models

由图19可知除Z1-3外，其余激励器都未起振成功，现分析其原因。忽略射流在喉道处的扩散，定义喉道剩余高度(喉道处未被射流挤占的高度)=-。如图19所示，后3个未稳定振荡的激励器的均小于，这会阻碍用于使射流换向的流体流入反馈管。定义相对喉道剩余高度=/。由图20可知，能令射流稳定振荡的激励器模型的均在1.15～1.50之间，故可以取其取值范围为[1.2,1.5]，则的计算式为

=+

(8)

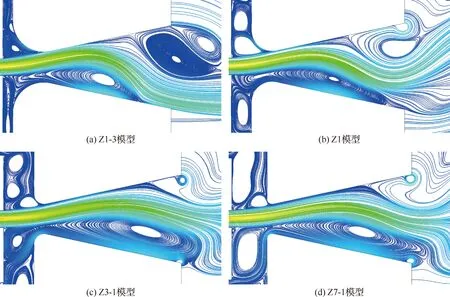
图19 T/4时Z组模型振荡器内的流场Fig.19 Flow field inside oscillator of Group Z models at T/4

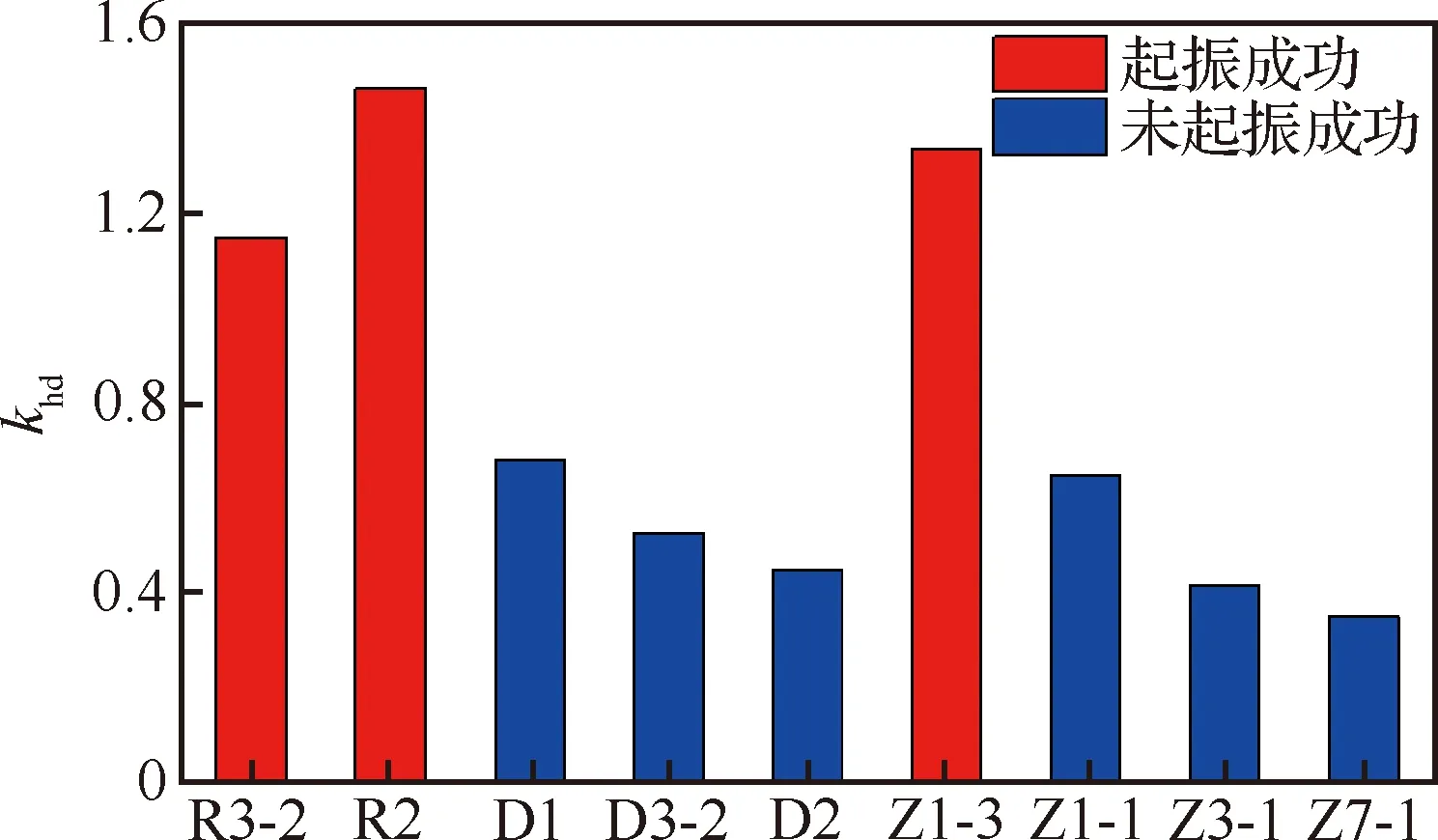
图20 各激励器模型的khdFig.20 khd of each actuator models

为了验证该结论，现将Z1和D3-2模型的增加至1.2，修正为H组模型HZ1和HD3-2(由于会随着的增大而增大，则使射流完全偏转的也会增大，故不再修正更大的模型)。如图21所示，射流在H组模型中均稳定振荡。图22表明射流已完全偏转，但扩大喉道使其不再满足射流偏转轨迹模型，射流与壁面接触的位置后移至扩张段，实际应用中应避免这种情况发生。

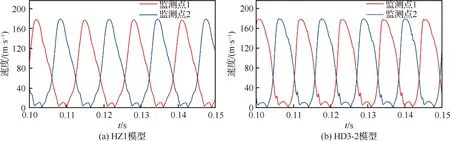
图21 H组模型监测点1和监测点2处的速度随时间的变化Fig.21 Time variation of velocity at monitoring points 1 and 2 of Group H models

综上所述，设计反馈段应首先由按式(8)求得能使射流稳定振荡的，再确定能使其完全偏转的，最后由式(7)求得符合射流偏转轨迹的。

图22 T/4时H组模型振荡器内的流场Fig.22 Flow field inside oscillator of Group H models at T/4

3 出流特性优化

本节研究了当入流条件一定时，影响激励器内部流动损失、0°偏角处停滞时间和射流扫掠角的因素，并给出减小速度损失和停滞时间、增大扫掠角的方法。

3.1 减小速度损失

本节首先以Z1-3模型为对象分析激励器内速度损失的来源，并给出其量级。射流振荡过程如图23所示，反馈通道内的流体在喉道处发生分离，产生分离涡(图23(a))；随着流体不断地从上反馈通道流入分离涡，其会不断变大，并挤压射流使之偏转(图23(b))；而一旦射流偏转至下壁面并封住下反馈通道口，流体就无法再流向上反馈通道口(图23(c))；射流会不断地从分离涡中带走质量，同时也会有流体从后方补入，在形成的回流中，其中一部分会流经反馈通道，并在下反馈通道处撞击射流、发生分离，从而完成一次振荡(图23(d))。在此过程中，射流与分离涡之间的流体质点不断地进行动量交换，发生剧烈的碰撞和摩擦，造成很大的能量损失，此即是激励器内射流速度损失的主要原因。

图23 射流振荡过程Fig.23 Jet oscillation process

反馈段和扩张段处射流中心速度的变化如图24所示(对应图23(c))，图中的拐折是因为气流撞击到了壁面，由图可知振荡器内的速度损失很大。由于其主要来自于射流与分离涡之间的动量交换，因此要尽量消除扩张段内无益于射流偏转的旋涡。风洞试验表明，当激励器的吸气位置越靠近吹气位置时，其对分离的控制效果越好，故本节将通过截短扩张段来减小速度损失。

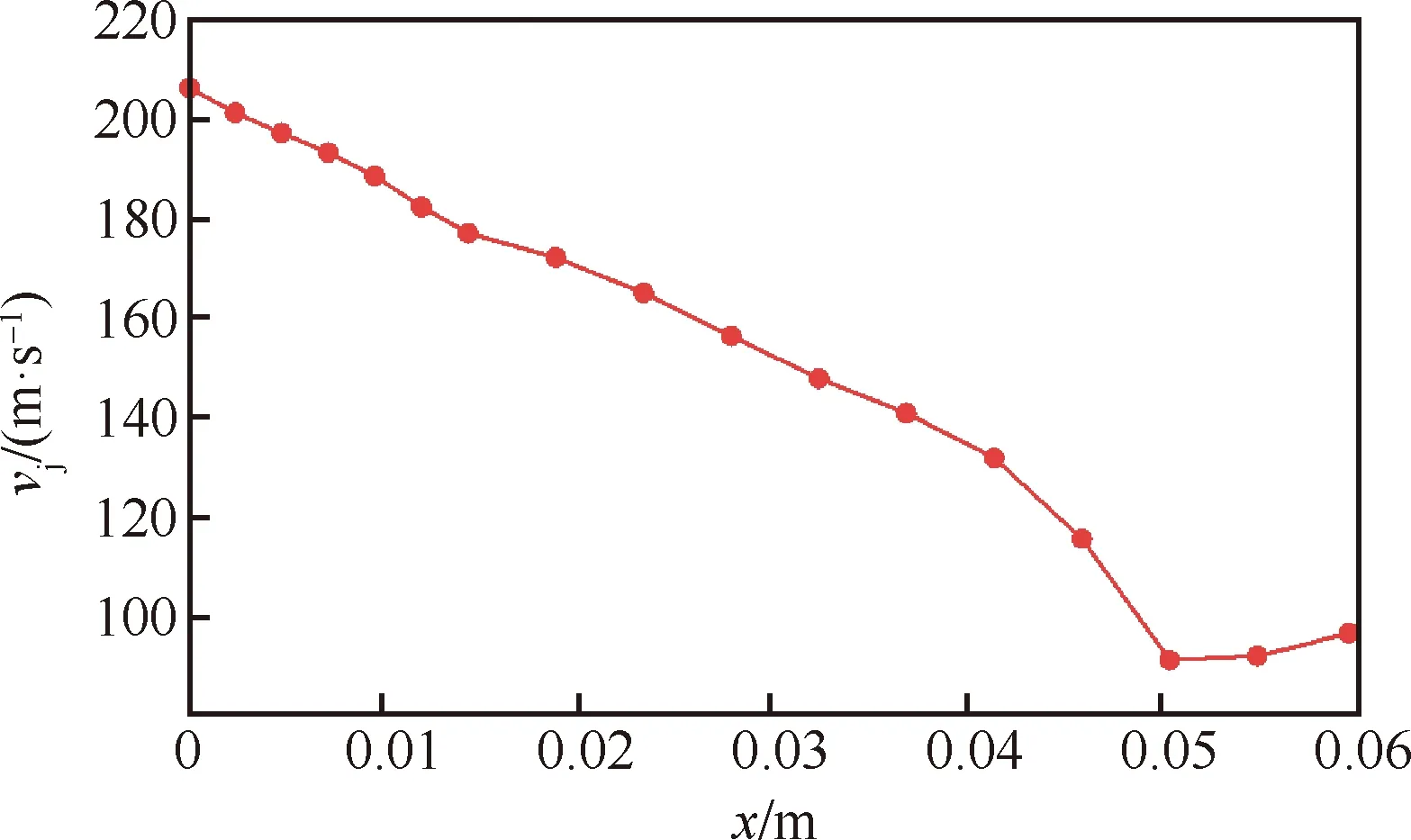
图24 Z1-3模型反馈段和扩张段内vj随x的变化Fig.24 Variation of vj with x in feedback and expansion sections of Z1-3 model

为了不影响激励器的起振特性，本节在当射流偏转至壁面时，扩张段内射流撞击另一侧壁面的位置将扩张段截短，如图25所示。现将Z1-3和HZ1模型截短，生成L组模型LZ1-3和LHZ1，其分别为5.60和6.16。

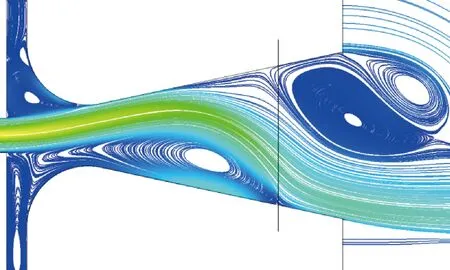
图25 扩张段截短位置Fig.25 Truncation position of expansion section

监测上述4个模型(下称LZ组)在/2时振荡器出口处的射流中心速度，由表4可知，截短扩张段可以减小速度损失。

表4 扩张段截短前后vje的变化

3.2 减少停滞时间

现以Z1-3模型为对象来说明射流的停滞现象，如图26所示。射流首先在分离涡的作用下偏向一侧，如果涡强较大，其会被吸附在大偏角处，从而发生停滞。当分离涡脱落后其会自动回偏并保持在0°偏角位置，从而再次发生停滞，直至下一个分离涡形成并挤压射流偏向另一侧。

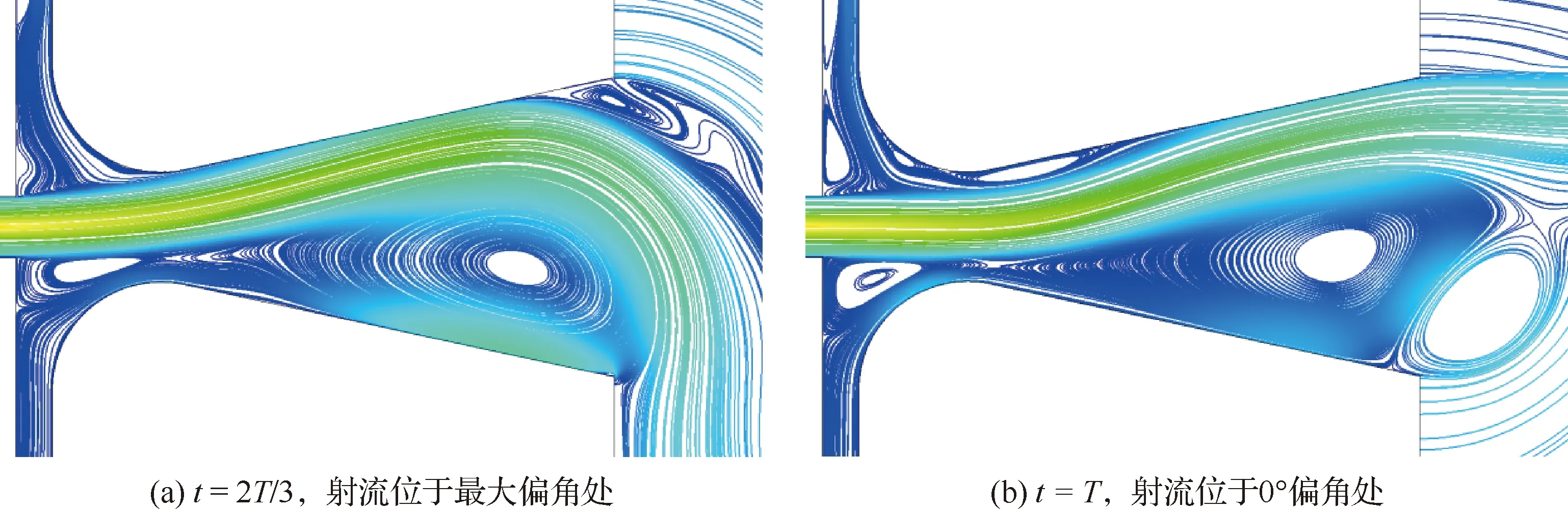
图26 Z1-3模型中射流从最大偏角处回偏至0°的过程Fig.26 Process of jet returning from maximum deflection angle to 0° in Z1-3 model

为了研究射流的停滞现象，现分别由监测点3和监测点4监测LZ组模型中射流在最大偏角和0°偏角处的停滞时间和，并以匀速系数=/来度量射流在不同偏角处扫掠速度的均匀性。如果射流在这两处停滞时间较长，监测点处的流速首先会发生突增，而后做小幅振荡(这是由流场的非定常性所致)，最终大幅回落；如果停滞时间较短，则监测点处的流速会在发生突增后迅速回落。由于监测点只能监测到射流贴附于扩张段上壁面时的停滞时间，因此实际值应为监测值的2倍。为了方便研究，定义监测点处的流速从开始突增到完成回落所用时间的2倍为停滞时间。

定义一个周期内的无量纲时间=/，则计算结果如图27和表5所示。由表可知，在一个周期内，LZ1-3模型中的射流有75.8%的时间都停滞在0°偏角处，而射流在LHZ1模型中的接近1，这表明其扫掠速度均匀性良好。产生该现象的原因是LHZ1和HZ1模型的较大，故较高，射流回偏至0°偏角处后能够及时被新的分离涡挤压至一侧。因此只要提高，加快分离涡的形成速度，就能够减少。

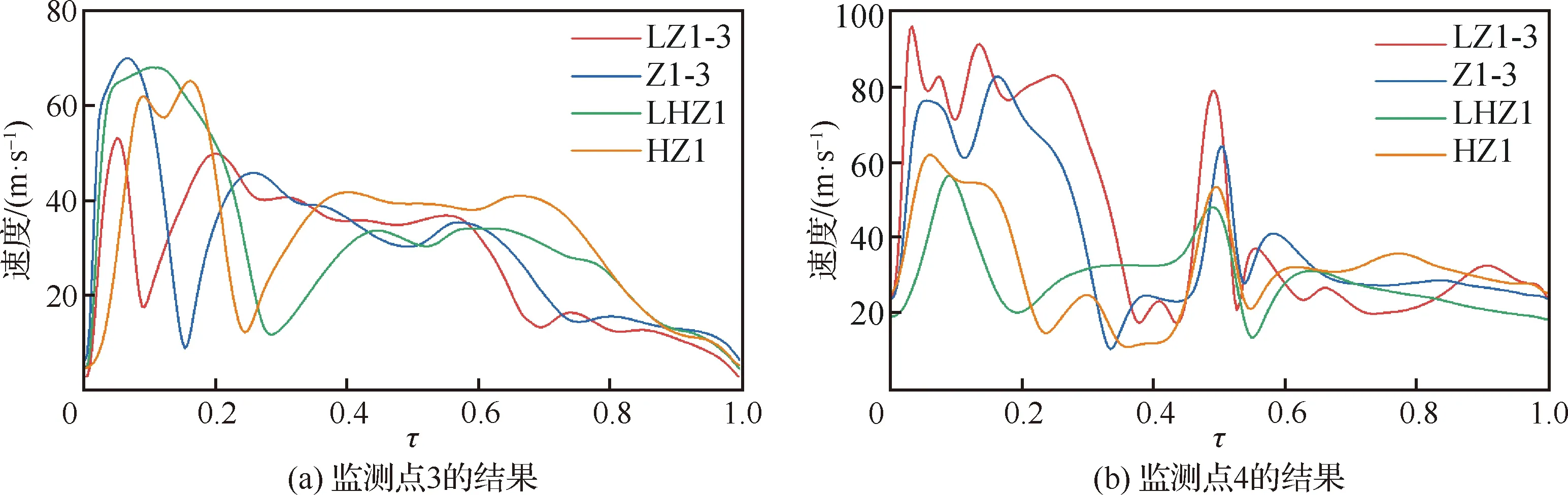
图27 LZ组模型监测点3和监测点4处速度随τ的变化Fig.27 Variation of velocity with τ at monitoring points 3 and 4 of Group LZ models

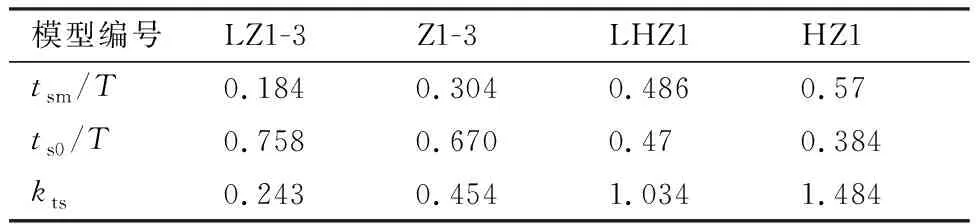
表5 LZ组模型的停滞时间和ktsTable 5 Stagnation time and kts of Group LZ models

3.3 增大射流扫掠角

本节讨论当流速给定时，振荡器几何参数对射流扫掠角的影响。如果旋涡能够提供射流偏转所需的向心加速度，则射流就会贴着旋涡偏转，现建立模型定性分析影响的几何因素。假设射流的质量都集中在其中心线上，则该线上质量微元做定轴转动所需的向心加速度为

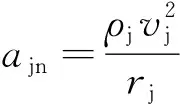
(9)

式中：为射流中心线在该点的曲率半径。

由于旋涡在射流中心处产生的向心加速度难以计算，现以旋涡边界处的向心加速度表示其对射流的吸引能力，的表达式为

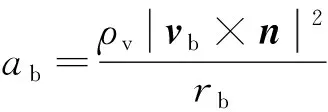
(10)

式中：为旋涡内流体密度；为旋涡边界处的速度矢量，方向与边界相切；为涡核到该点的距离；为的指向。当越大，与越接近时则射流越易于偏转。

由式(9)和式(10)可知，分离涡对射流有大小和形状两方面影响，对于大小，旋涡尺寸越大，与、与(为旋涡边界处的速度大小)就越接近，因此也越接近，射流会更易偏转。对于形状，现将Z1-3模型的由12°改为6°；保持HD3-2模型的、、和扩张段面积不变，按式(7)计算并缩短，生成A组模型AZ1-3和AHD3-2，射流在两者中达到最大偏角时的流场如图28所示。尽管两模型内旋涡大小不同，但由图可知旋涡越细长，出口处旋涡边界的曲率半径就越小，则所需的就越小，就越大，但此时的却较大，且|×|较小，能提供的较小，则射流难以偏转。

现以扣除射流所占面积之后的扩张段面积近似表示射流偏角达到时扩张段内分离涡的面积，如图29所示。所对应的当量旋涡半径为、旋涡长宽比为，其中=/。忽略射流的扩散，定义与射流半宽度/2之比为旋涡大小系数，以描述旋涡的形状。所有起振成功模型的相应参数和如表6所示。

图28 A组模型中射流达到最大偏角时的流场Fig.28 Flow field when jet reaches maximum deflection angle in Group A models

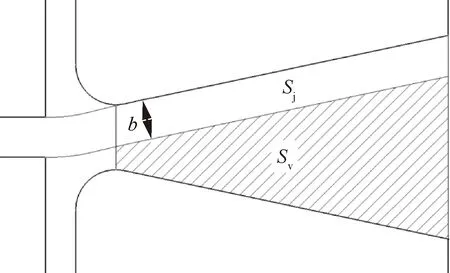
图29 Sj与Sv示意图Fig.29 Schematic diagram of Sj and Sv

表6 起振成功模型的旋涡大小与形状参数及θjTable 6 Vortex size, shape parameters and θj of model with successful start-up

接下来研究和对的影响，定义诱导系数=，将按式(11)无量纲化为角度系数，则起振成功模型的和如表7所示。

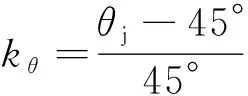
(11)

现以式(12)所示的函数拟合和，如图30所示，其中=-1.33，=-1.16，=1.75。HD3-2的值明显偏离拟合曲线，但其值较高(文中未给出)，这说明分离涡对射流的吸引能力强，故可以较好地衡量分离涡对射流的诱导作用。

表7 起振成功模型的kRA和kθTable 7 kRA and kθ of model with successful start-up

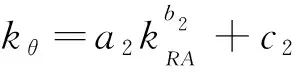
(12)

由于是的分母，其对影响更大，且增大会增大射流与旋涡的接触长度，从而增大速度损失。由表6可知，射流在AHD3-2模型中的达到了±110°，因此减小是增大较好的方式。

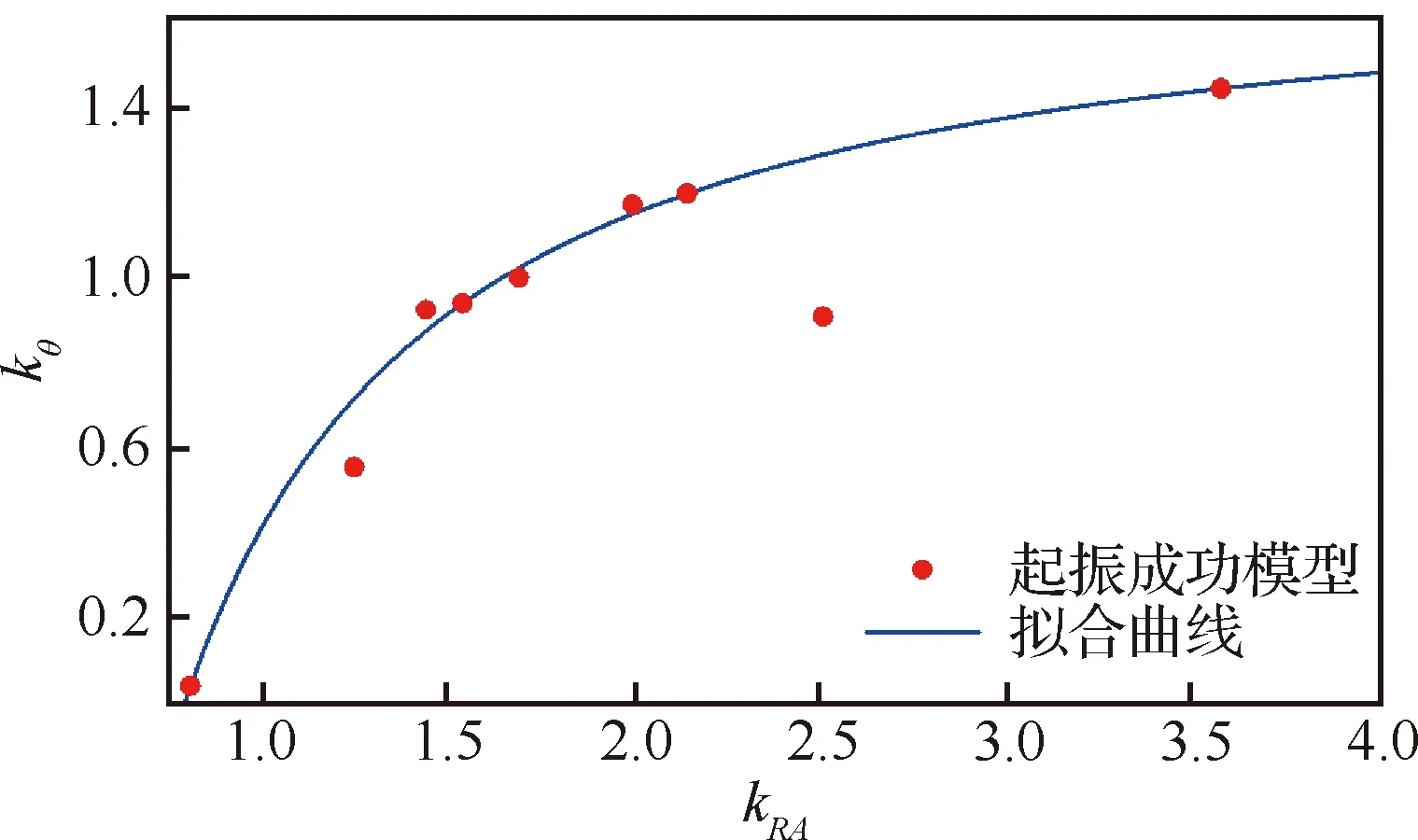
图30 kRA对kθ的拟合结果Fig.30 Fitting result of kRA to kθ

4 频率模型建立

本节将从射流振荡的物理过程出发，建立其振荡频率模型，并分析影响频率的因素。射流偏转是由于受到了分离涡的挤压，本节假设分离涡的大小仅取决于从反馈通道注入的流量。则射流偏转过程可以描述为：反馈通道从射流的一侧抽走流量，并在另一侧注入，射流受到挤压并逐渐偏转，直到射流由一侧偏转至另一侧壁面。此时反馈通道口被射流封住，则输运过程结束。记该过程中由反馈通道输运的质量为临界质量。

半个周期内，所有起振成功激励器的反馈通道中各时刻平均流速与最大平均流速之比随无量纲时间的变化如图31所示，由图可知正弦函数可以较好描述反馈通道内流量随的变化规律。假设反馈通道和分离涡内流体的密度相同，令通道内平均流速随变化的幅值为，则随的变化为

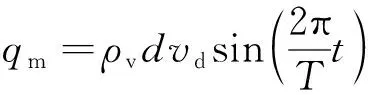
(13)

在正半周期上的积分应为，如式(14)所示，则可由式(15)表示。图32比较了的数值模拟结果和由式(15)预测的结果，两者较吻合，说明所建模型合理。

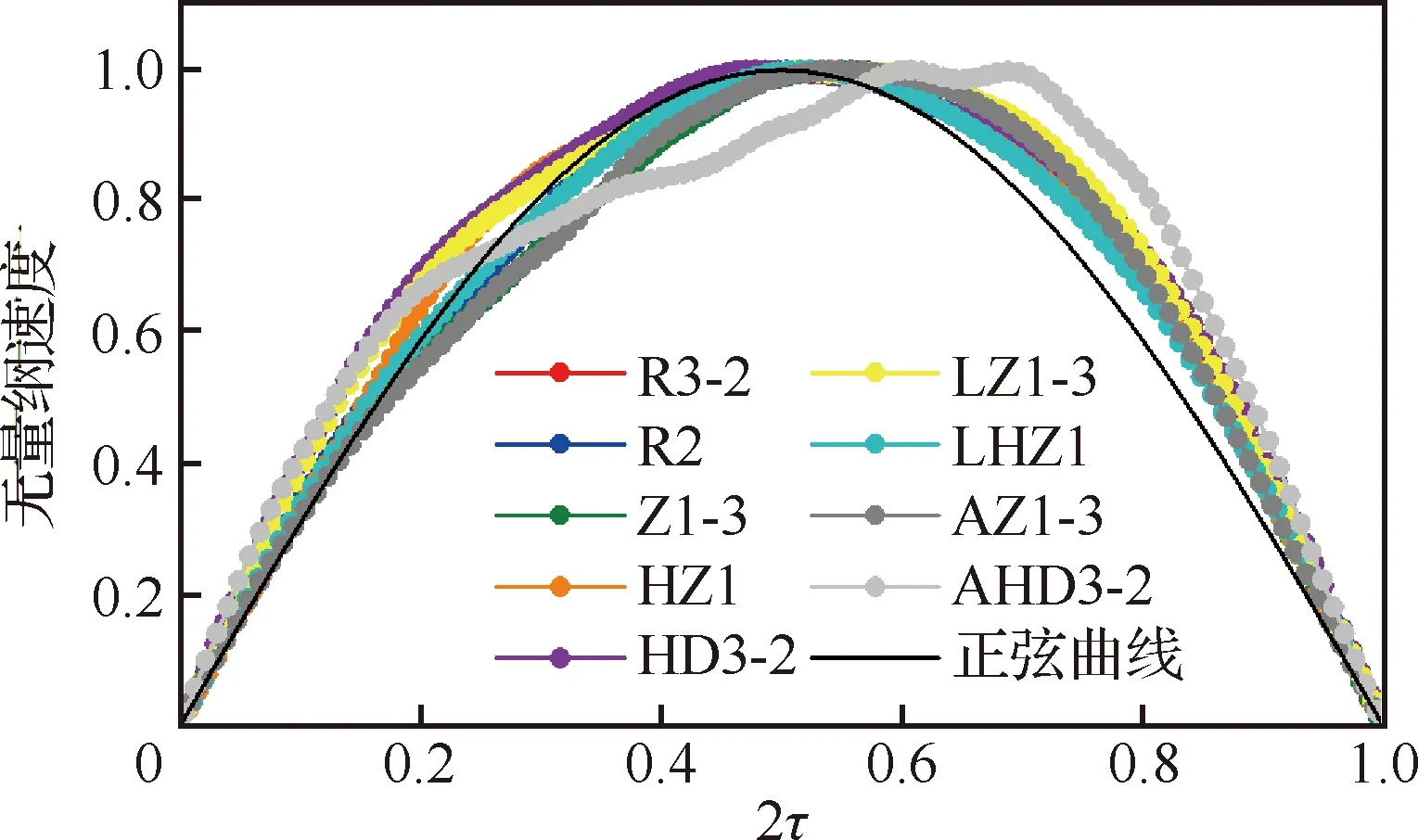
图31 正弦函数的拟合效果Fig.31 Fitting effect of sine function

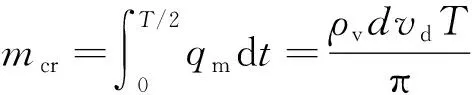
(14)

(15)

由式(15)可推知，当其他条件一定时，增加或可以直接增大流量，减少到达的时间，从而提高；而增大和会增加壁面摩擦的作用距离，这使得沿程损失增大，导致减小，从而减小。

为了探究引射器主流入口处的总压与远场静压之比对的影响，现以Z1-3为研究对象，改变并计算，如图33所示，两者基本呈线性关系(=2时收敛喷管发生拥塞)，增大时入流和回流流速提高，因此会增大，从而提高。

接下来研究影响的几何因素。是射流偏转至一侧壁面时，分离涡内的流体质量，记此时的分离涡面积为。由于式(15)中的几何参数只有，当改变时，由式(7)和式(8)知，和也会改变，因此本节将研究、和的关系。

易知和越大时越大，故取组合参数=tan，以式(16)对其与进行拟合，拟合结果如图34所示，其中=3.80，=0.017 3。

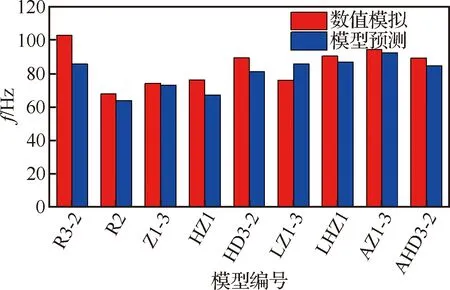
图32 f的数值模拟与模型预测结果比较Fig.32 Comparison between numerical simulation and model prediction of f

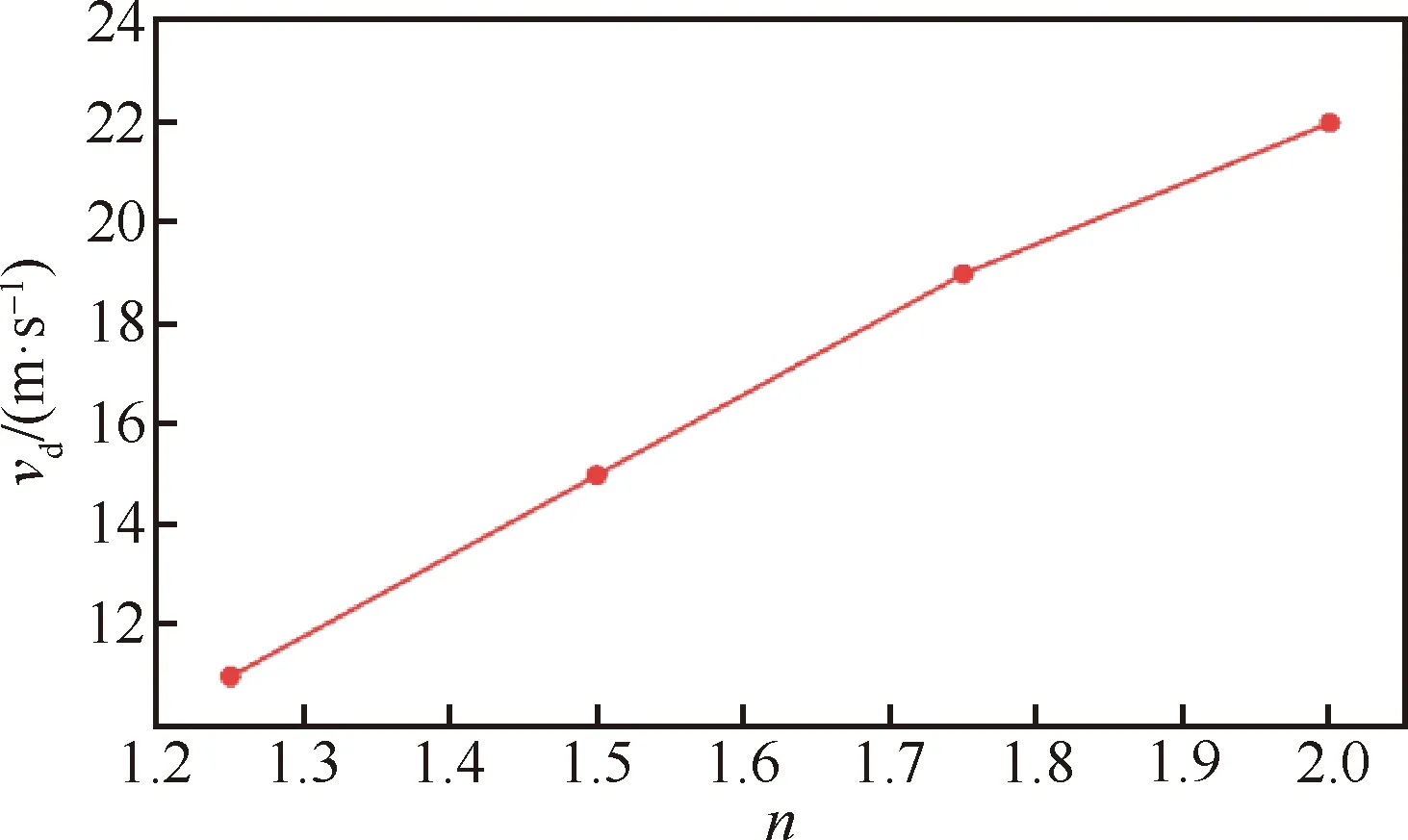
图33 vd随n的变化Fig.33 Variation of vd with n

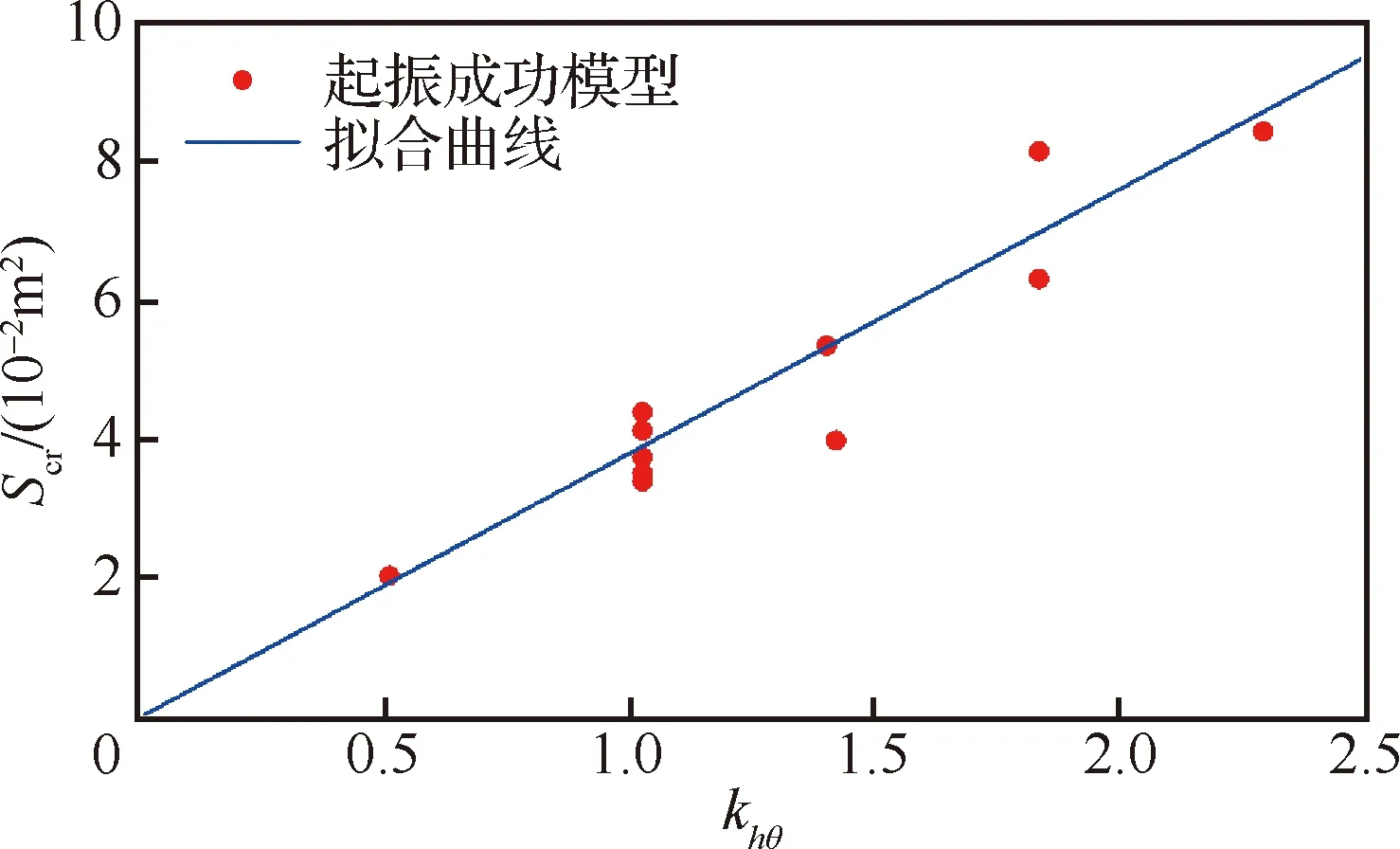
图34 khθ对Scr的拟合结果Fig.34 Fitting result of khθ to Scr

由图可知两者近似成正比。而式(8)表明，应为的倍，因此可以通过改变来调节。

=+

(16)

5 结 论

1) 喉道高度和反馈段长度决定了射流能否起振成功，而扩张角则决定了射流能否附壁。合适的喉道高度保证了在一个振荡周期内会有足够多的流体进入反馈通道，这些流体会撞击射流，发生动量变化，产生使射流偏转的加速度。而要使射流完全偏转，则需要足够长的加速度作用距离，即反馈段长度。为了使射流附壁，需要扩张角与射流偏角相同。综上所述，在设计激励器外形时，应首先按喉道剩余高度为反馈通道宽度的1.2～1.5倍确定喉道高度，再确定能使射流完全偏转并与扩张段壁面相切的反馈段长度和扩张角。

2) 在射流偏转至极限高度时扩张段内射流撞击壁面的位置将扩张段截短可以在不影响激励器起振特性的前提下减小射流速度损失；提高振荡频率会减少射流在0°偏角处的停滞时间。

3) 扩张段内的分离涡越大，长宽比越小，则射流扫掠角越大，长宽比对扫掠角的影响比分离涡大小更明显。

4) 其他条件一定时，改变反馈通道宽度和相对喉道剩余高度会分别改变注入的流量和完成偏转所需的流体质量，从而影响频率。改变入流流速和反馈通道长度、扩张段长度则是通过改变注入激励器和其损耗的能量来影响反馈通道内的流速，从而间接改变流量以影响频率。

致 谢

感谢西北工业大学张学鹏和刘明奇为本课题提供了计算资源。