消振电力作动器用位置环解耦控制策略

郝振洋，王涛，曹鑫，朱涛

南京航空航天大学 自动化学院，南京 210016

直升机因其高机动性、悬停、垂直起降等优点，在民用和军事方面得到了广泛应用，随之而来的旋翼振动和气动噪声问题也日益突出。近年来，消振电力作动器因其效率高、体积小和重量轻等优势已成为直升机主动振动控制领域的研究热点。相比于振动被动控制系统，主动振动控制技术通过传感器采集机体的振动信息将其送至上位机中解算出频率、幅值、方向相同相位相反的作动力信息驱动作动器执行，减振效率达85%以上，极大的削弱了旋翼直升机由于主旋翼等部件带来的振动问题，从而改善了驾驶员的驾驶环境。

国外在直升机主动振动控制领域做了大量的研究工作，美国学者Garnjost在其专利中提出适用于直升机的消振电力作动器。该作动器两侧各有一个输出力模块，每个模块都由电机通过齿轮组驱动一对反向旋转的偏心质量块来产生垂直方向的离心力，最终作动力为两个模块输出力的叠加，这种方案大大减轻了减振系统的重量。文献[8-9]介绍了韩国航空工业研究机构在直升机减振控制装置以及AVCS(主动振动控制系统)所做的研究工作，他们设计的消振电力作动器经过了地面和飞行测试，获得了最佳AVCS布局和飞行测试结果。其中文献[8]通过实验测试了KUH(韩国通用直升机)的机体振动主频率，设计了主动振动控制装置，不仅适用于直升机等，也为在其他需要振动控制邻域的普遍使用提供了可能。文献[9]验证了将AVCS应用在Surion直升机上的性能，通过对飞行试验结果的分析机体振动水平降低70%左右，将会应用于开发新的直升机及现有直升机的改良工作中。文献[10]介绍了美国洛德公司的圆形力发生器的主动振动控制技术，相比于传统的线力AVCS不仅能输出更多方向的消振力，还具有重量轻、功耗低和模块化等优点，有效提高了系统的性能。国内对于直升机用消振电力作动器控制技术的研究还处于起步阶段，消振电力作动器技术大多用于船舶等频带较窄、消振精度要求不高的场合。哈尔滨工程大学的韩广才课题组采用非线性变结构滑模控制算法，实现了作动器频率和振幅的自动控制，结果表明相位差在180°±10°范围内减振效果是可行的,但超出这一范围,减振效果并不明显。南京航空航天大学航空宇航学院将压电叠层作动器用于直升机主动振动控制，提出了机身/压电叠层作动器耦合优化法，并对机身模型进行了控制仿真，有显著的振动抑制效果。中国直升机设计研究所针对离心式作动器同时输出力幅值、相位和频率跟踪以及输出力跟踪误差问题，提出了基于滑模变结构控制的变滑模面控制方法, 仿真结果表明离心式作动器跟踪精度和输出力的跟踪响应速度得到了提高并且系统具有较好的抗干扰能力，但是在仿真环境下很多因素并不能够真正的得以体现。

消振电力作动器采用的是多台电机驱动偏心质量块的形式输出减振力，属于多电机协调控制范畴。传统并行控制策略采用给每台电机发送给定相位同步执行的方式，控制算法相对简单易于实现，但是系统的输出侧存在强耦合，状态变量之间相互干扰影响了消振电力作动器控制系统的输出力精度。基于此，本文提出的消振电力作动器用位置环解耦控制策略通过控制系统位置环的交叉耦合解决了传统并行控制策略中存在的输出端强耦合问题，既改善了系统中控制变量相互耦合带来的干扰，也更加方便控制器的参数设计与实现，适合应用于主动振动控制系统这类对控制精度要求较高的场合。

为了将消振电力作动器控制系统从仿真验证推向工程应用，需要系统具备良好的动稳定性能和抗干扰性。本文首先对比了传统的并行控制策略，所提控制策略改善了控制系统输出变量相互耦合带来的干扰。其次，结合主导极点法和广义频率法设计出了位置环控制器的PID参数，并通过回差阵奇异值法等MIMO系统稳定裕度计算方法分析了系统的动稳态性能。最后，研制出了原理样机，搭建了实验平台，实验验证了控制策略的有效性和参数设计的合理性，这也为后期的地面减振实验和工程应用提供了理论基础。

1 消振电力作动器控制策略

1.1 消振电力作动器输出力原理

如图1所示为消振电力作动器消除直升机振动的典型原理示意图，安装在驾驶员座舱等部位的加速度传感器采集由主旋翼和航空发动机等旋转部件传递到基础结构的激振力信息并发送到控制器中进行解算，得到与激振力频率、力幅和方向相同，但相位相反的作动力指令并驱动消振电力作动器执行。消振电力作动器作为直升机主动振动控制系统的“心脏”，驱动偏心质量块旋转输出所需的作动力抵消传递到基础结构的激振力实现减振控制。

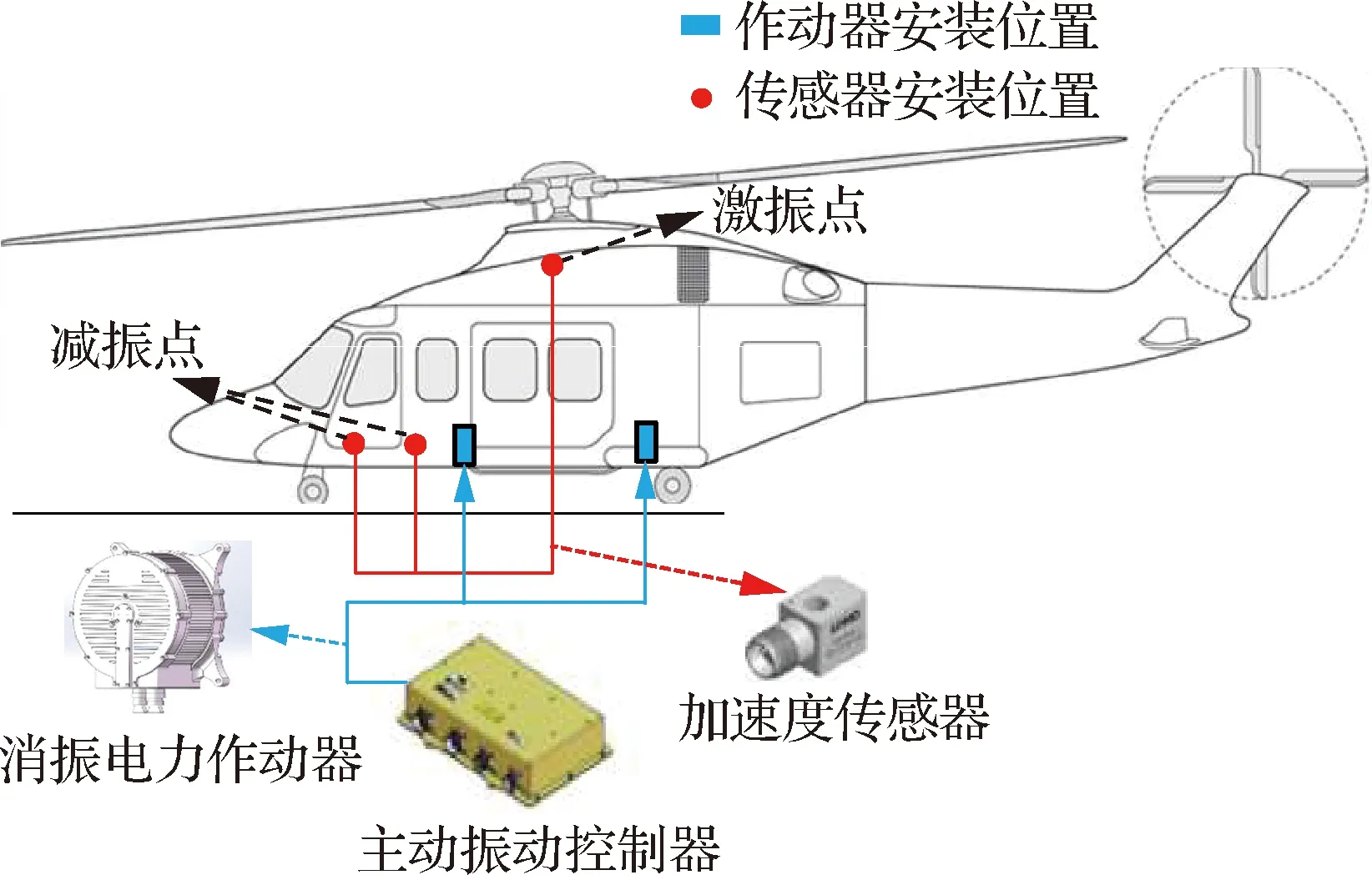
图1 直升机减振典型原理示意图Fig.1 Schematic diagram of typical principle of helicopter vibration reduction

消振电力作动器既是直升机主动振动控制系统的执行机构更是核心环节，为了更好的设计消振电力作动器控制策略，首先需要对作动器的输出力原理进行分析。作动器内部前后对称的分布着一对偏心质量块，分别由两台电机驱动做同向同速旋转，如图2所示。

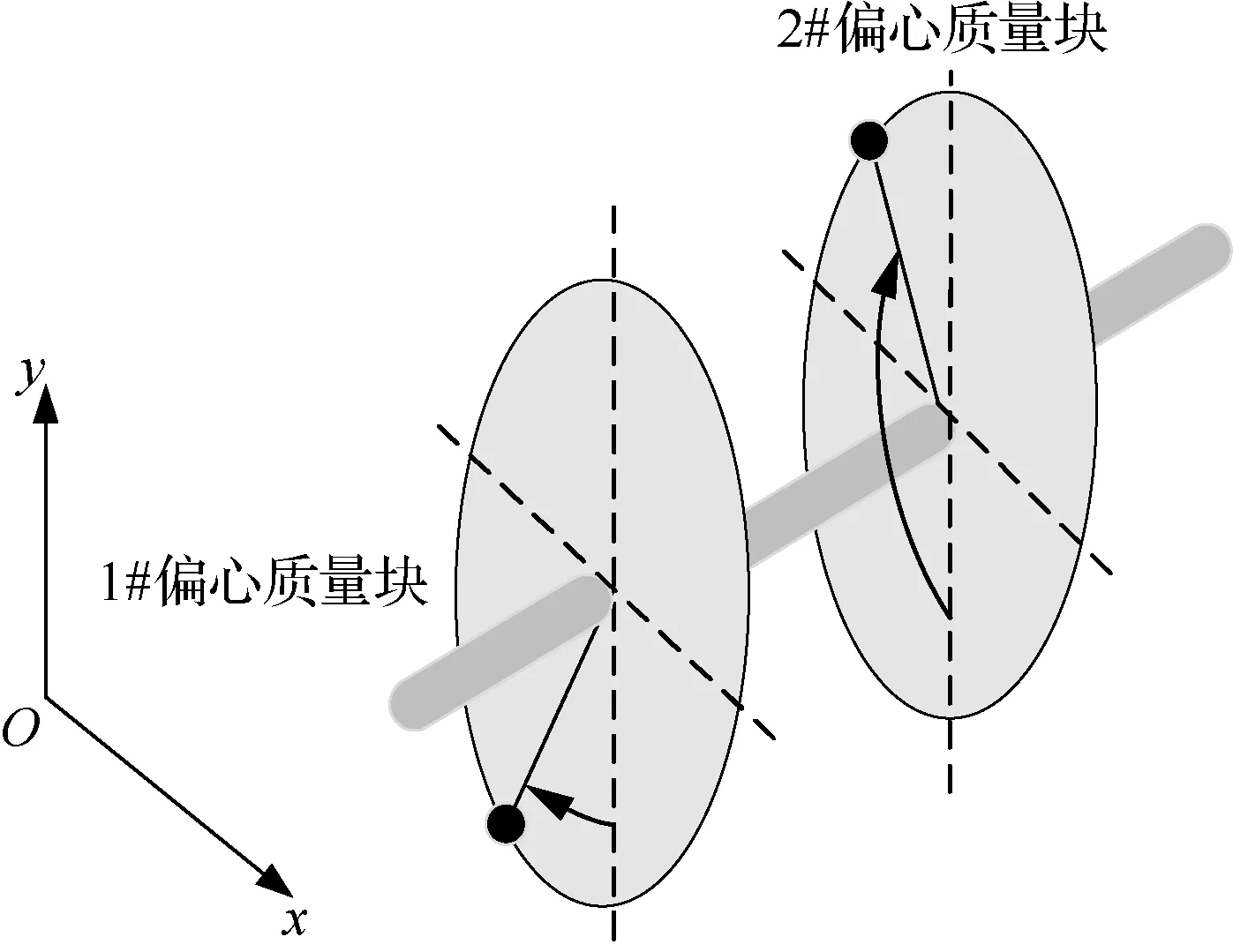
图2 作动器简化示意图Fig.2 Simplified schematic diagram of actuator

对偏心质量块进行受力分析，偏心质量块的重量为，偏心距为，假设两个偏心质量块同向旋转的频率相同为，受力分析图如图3所示。

图3 偏心质量块受力分析示意图Fig.3 Schematic diagram of force analysis of eccentric mass block

图3中：、、以及分别表示第个偏心质量块所受的离心力、离心力的水平分量、垂直分量和当前位置，其中=1，2。规定垂直向下为基准方向，偏心质量块顺时针旋转为正，可计算出偏心质量块所受离心力垂直分量和水平分量:

=cos

(1)

=sin

(2)

由式(1)和式(2)可得1#和2#偏心质量块合成输出力的垂直和水平分量。

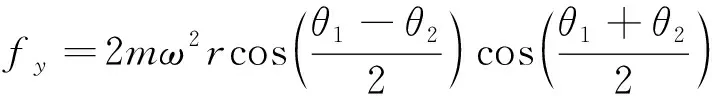
(3)

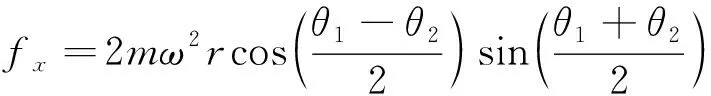
(4)

消振作动器合成矢量输出力表达式为

(5)

由式(5)可知，单台作动器输出的作动力是一个二维平面的圆形面力，圆的最大半径为2，如图4所示。

图4 单台作动器输出力轮廓图Fig.4 Contour diagram of output force of single actuator

通过控制偏心质量块的转速、两个偏心质量块位置差可以实现对输出作动力幅值和频率的控制，但是输出力的方向是时刻变化的，无法完成特定方向上的消振控制，因此需要将两个消振作动器配合使用从而输出特定方向上的相位可调的作动力。值得注意的是，不同消振作动器输出力的方向是相反的。

类似于式(5)，另一台作动器合成矢量输出力为

(6)

采用先控力幅，再控方向的策略，即

(7)

将两台作动器并列摆放，使各自的输出力在同一平面上，如图5所示。

图5 作动器摆放方式图Fig.5 Actuator placement diagram

因此两台消振作动器合成的矢量输出力为

(8)

相比于单台作动器只能输出频率、力幅可调的作动力，两台消振作动器协调可以通过控制偏心质量块的转速、位置和位置差输出频、相、幅和方向可调的作动力，从而可以在任意方向上实现消振控制。

1.2 传统并行控制策略

图6所示为传统并行控制策略下，消振电力作动器控制系统的控制框图。图中，dc和dc分别表示第个通道的直流电流输入和反馈量，下标dc表示直流侧；控制系统是四输入四输出系统，APR表示第个通道的位置环控制器(=1～4)；ASR为转速环调节器，ACR代表电流环调节器，其中电流环和转速环采用PI控制，位置环采用PID控制。

位置环的给定可以表示为

=+

(9)

式中:和分别表示给定偏心质量块的位置和初相；为给定偏心质量块的转速，实现消振控制的关键在于实现对单个偏心质量块相位的精确跟踪。理想情况下，可以认为四个通道的位置环内环即转速环闭环传递函数是完全一致的，用()表示。根据叠加原理，传统并行控制策略下从输入侧到输出侧的传递函数矩阵可表示为

(10)

图6 基于传统并行控制策略下系统控制框图Fig.6 System control block diagram based on traditional parallel control strategy

由式(10)可以看出，传统并行控制策略下系统传递函数矩阵非对角线元素不全为0，这是由于控制系统的输出端存在强耦合，控制变量相互干扰，从而影响了输出力的精度，并且由于传递函数矩阵为耦合矩阵，也不利于参数的设计。因此这种控制策略不适用于高精度的消振电力作动器控制系统。基于此，本文提出了消振电力作动器用位置环解耦控制策略。

1.3 位置环解耦控制策略

图7所示为消振电力作动器用位置环解耦控制策略框图，通过位置环解耦控制部分去补偿系统输出端的交叉耦合控制部分从而实现解耦目的。

(11)

图7 消振电力作动器用位置环解耦控制策略框图Fig.7 Block diagram of position loop decoupling control strategy for vibration damping electric actuator

显然，位置环解耦控制策略下系统的传递函数矩阵为对角矩阵，无论是从控制上还是控制器的参数设计上，相比于传统并行控制策略都具有更大的优越性，更加适合主动振动控制这类对控制精度要求较高的场合。

位置环解耦控制策略可以实现消振电力作动器控制系统的解耦控制，避免了控制变量之间的强耦合影响，同时将位置差信号作为控制信号，实现了偏心质量块的位置差值同步。

2 位置环解耦控制系统参数设计

为了提高消振电力作动器控制系统对于输入指令的快速跟随性和稳定性，位置环解耦控制部分采用了PID控制，本文通过主导极点法和广义频率法对位置环参数进行了理论性的设计，以期提高系统的动态性能和鲁棒性。

2.1 广义频率法与主导极点法

广义频率法是约束系统稳定裕度的方法，可以只通过一个参数以分析计算的形式指定系统的稳定裕度。

奈奎斯特稳定判据是以虚轴为标准对控制系统的稳定性进行判别的，将=j带入系统开环传递函数()，根据(j)逆时针包围(-1,j0)点的圈数和系统的开环极点分布，来判断系统闭环传递函数的极点在虚轴两侧的分布情况。同样，也可以不用虚轴而用任意一条线作为标准而使系统本身具有一定的稳定裕度。基于此，广义频率法使用图8中所示的两条虚折线作为判断标准，其方程为：=-+j，>0且为一常数，用以判断控制系统的闭环极点是否落于图8中的阴影部分。图中是折线与虚轴的夹角，显然=tan，称为系统的衰减系数，也表示系统的稳定裕度。由于每一对复平面的闭环极点都有一个衰减系数与之对应，其中最小的被指定为系统的衰减系数，即=min()，衰减系数可以作为系统一个稳定裕度的标准，在设计参数时指定系统稳定裕度的大小。通过广义频率法，可以使系统具备一定的稳定裕度即鲁棒性，为了使消振电力作动器控制系统可以快速的跟随输入指令，还需要保证系统具备良好的动态特性，在这里主导极点法被使用。

图8 广义频率特性图Fig.8 Generalized frequency characteristic diagram

对于式(12)形式的系统开环传递函数：

(12)

式中：()是互质不可约的，已知控制器的传递函数为()=++(为比例系数；为积分系数；为微分系数)，则单位负反馈系统的闭环特征方程为

1+()()=0

(13)

假定主导极点为=-±j，其他非主导极点的实部必须小于-，一般取为3～5。将主导极点代入式(13)中，可以获得复数方程

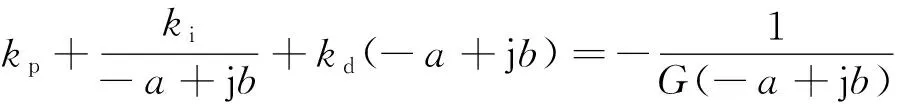
(14)

比较式(14)两边的实部和虚部，可以得出

(15)

式中:和满足：

(16)

(17)

式(15)可以保证=-+j是闭环系统的极点但是不能保证是主导极点，因此还需要加一个约束条件。将式(15)代入式(13)可以得到：

(18)

(19)

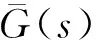
2.2 系统参数设计

表1和表2分别给出被控对象的具体参数和系统的性能指标。

表1 电机参数Table 1 Motor parameters

表2 性能指标Table 2 Performance index

根据文献[20]中的环路参数整定方法，对电机电流环和转速环的PI参数进行设计，参数结果见表3。

表3 电流环和转速环参数Table 3 Parameters of current loop and speed loop

由表3可得控制系统各通道内环即转速环的闭环传递函数为

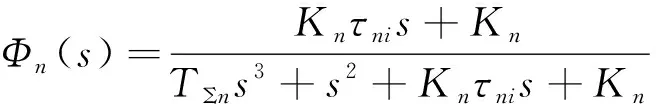
(20)

式中：为转速环积分时间常数；Σ为转速环滤波电路与电流环等效一阶惯性环节的时间常数，数值为0.7 ms。

基于此，将图7用复频域传递函数框图表示，如图9所示。图9中，()表示4个通道的位置环控制器，()为4个偏心质量块的实时位置，其中=1～4。将位置环控制器的传递函数表达式()代入式(11)中，可进一步将系统传递函数矩阵表示为

图9 位置环解耦控制系统传递函数框图Fig.9 Transfer function block diagram of position loop decoupling control system

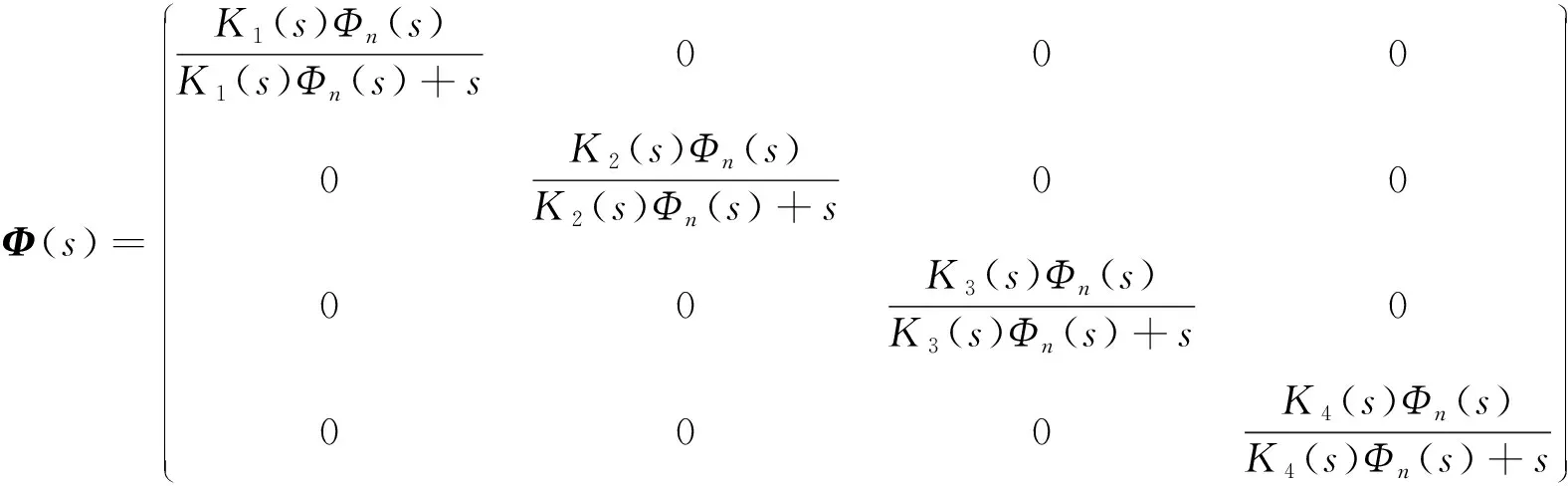
(21)

由于闭环传递函数矩阵是对角矩阵，所以可以通过设计单个通道的闭环传递函数来使整个系统的性能达到最优。以1#通道为例，其闭环特征方程为

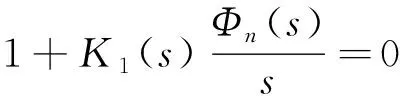
(22)

首先确定控制系统的动态性能，见表4。由表4可以确定主导极点为=-45±j45。根据式(15)可以计算出位置环控制器的PID参数之间关系为

(23)

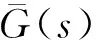
表4 控制系统动态性能设计Table 4 Control system dynamic performance design

表的开环和闭环极点Table 5 Open-loop and closed-loop poles of

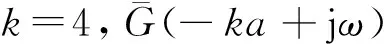
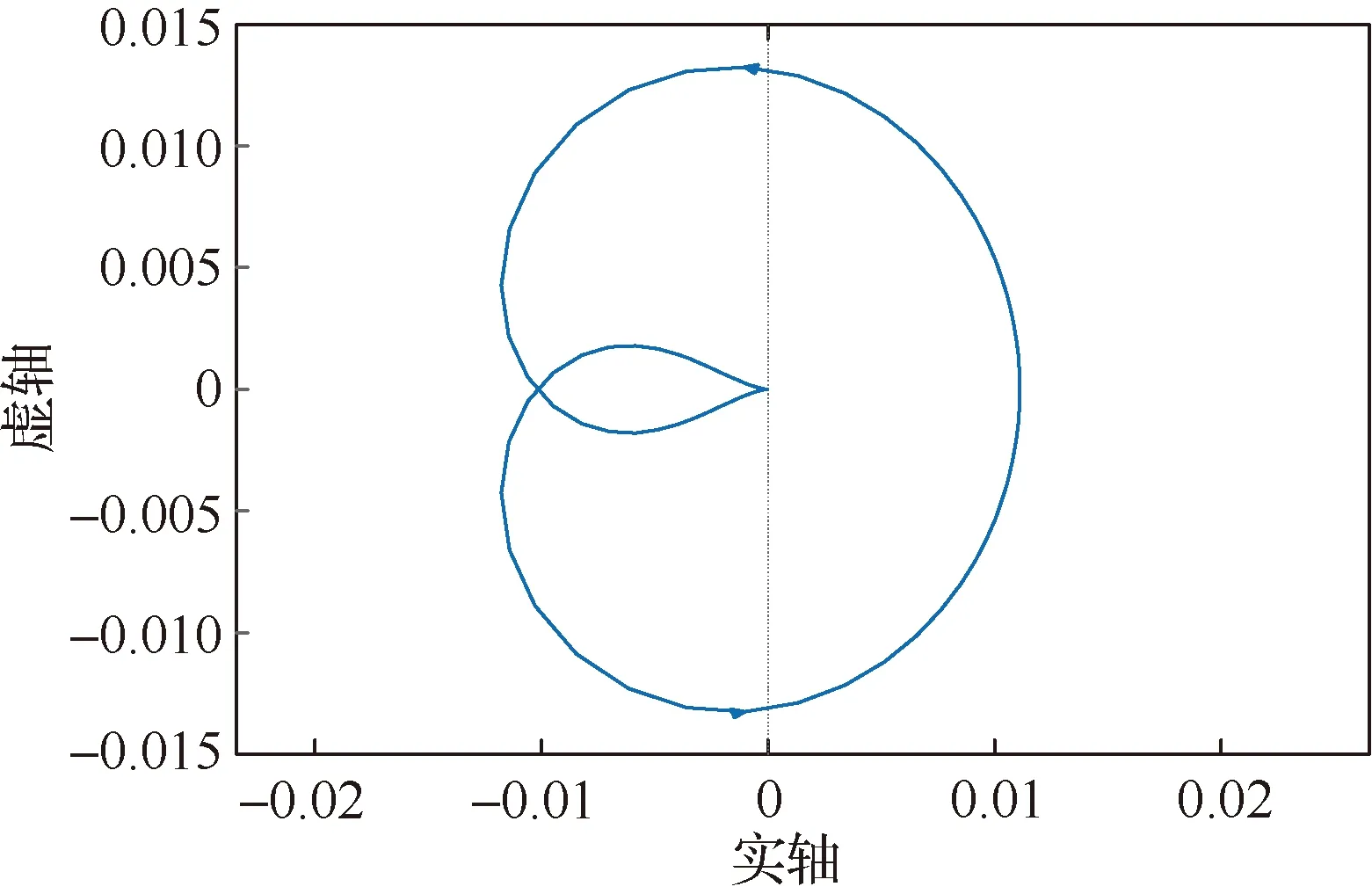
图的奈奎斯特曲线

由图11可得，与之对应得取值范围是>0， 综上所述，∈(89.496，100)，由式(23)可以计算出与之对应的和。

图的奈奎斯特曲线

2.3 两种控制策略下系统动稳态性能对比

由1.2和1.3节从传统并行控制策略和位置环解耦控制策略的传递函数矩阵来看，在控制和参数设计上，位置环解耦控制策略更具有优势。下面通过对两种控制策略下系统的动稳态性能仿真对比来验证理论分析的正确性。

根据2.2节计算出的位置环参数范围，画出两种控制策略下系统的单位阶跃响应曲线，如图12所示。可以看出，传统并行控制策略下系统单位阶跃响应超调量为=30%，调节时间1=0.22 s。 相比之下，位置环解耦控制策略下系统的单位阶跃响应超调量仅为σ=20%，调节时间2=0.12 s。 显然，采用位置环解耦控制策略系统具有更加优良的动态性能，能够更加快速的实现对给定指令的跟随，并且调节过程中的冲击较小。

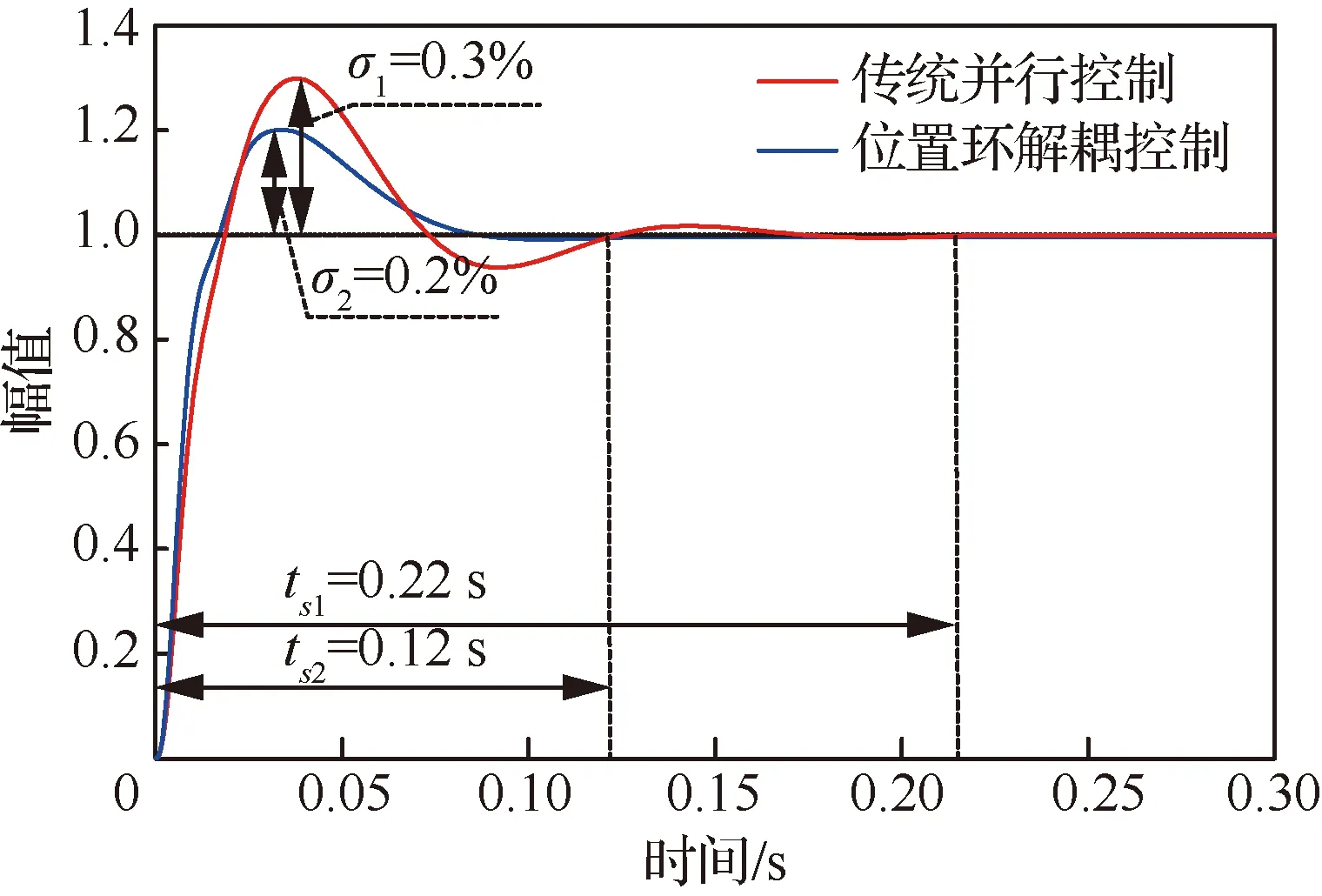
图12 两种控制策略下系统单位阶跃响应对比图Fig.12 Comparison chart of system unit step response with two control strategies

对于消振电力作动器控制系统，不仅要关注其动态性能，更要考虑在稳定运行时，系统的鲁棒稳定性。由式(10)和式(11)可知，两种控制策略下消振电力作动器控制系统都属于多输入多输出系统，不同于传统的单输入单输出系统，稳定裕度的计算不能采用绘制伯德图分析，文献[21-22]为多输入多输出系统稳定裕度的计算提供了解决思路，分别有回差矩阵奇异值法、回差矩阵特征值法以及逆回差矩阵奇异值法。

两种控制策略下的系统稳定裕度计算结果如表6和表7所示。由于3种计算方法的理论推导过程都存在各自的保守性，因此可以将3种方法所求得的稳定裕度结果结合起来一起考虑, 得到最终保守性较小的系统稳定裕度。由表6可得, 传统并行控制策略下系统保持稳定所容许的4个回路的增益可同时增大7.52 dB，或相位同时滞后53.04°。从表7可以看出，位置环解耦控制策略下系统的幅值裕度为11.21 dB，相角裕度为46.12°。相比于传统并行控制策略，位置环解耦控制策略下系统的幅值裕度更大即鲁棒性更强，同时相角裕度也更加接近45°最优值。

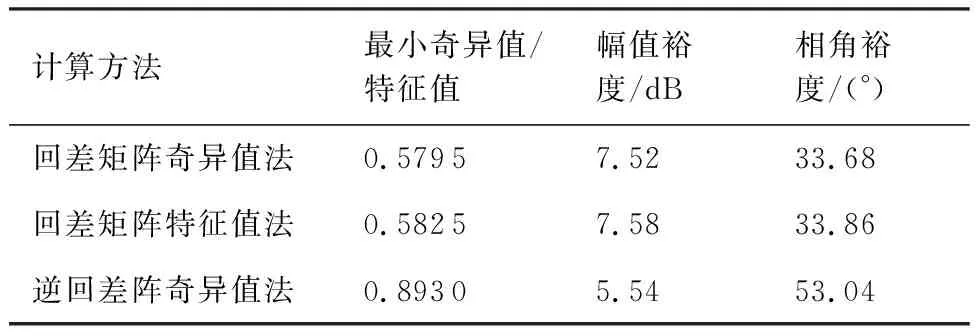
表6 传统并行控制策略下系统稳定裕度

表7 位置环解耦控制策略下系统稳定裕度

为了更加直观的对比两种控制策略下系统的稳定性能，通过仿真验证稳定裕度计算的正确性和合理性。由稳定裕度计算结果可知，在保证系统稳定的前提下，传统并行控制策略下系统各回路增益可以同时增大2.37倍，而位置环解耦控制策略下系统各回路增益可同时增大3.63倍。分别对两个系统输出力从3 000 N变化至1 000 N进行仿真，持续增加各回路增益，当增益增加至3.4倍时，传统并行控制策略下系统开始发散而位置环解耦控制策略下系统仍保持稳定，如图13所示。由图13可得，传统并行控制策略下系统的稳定裕度为10.63 dB。

继续增大各回路的增益至5.52倍，位置环解耦控制策略下系统也开始无法收敛，因此位置环解耦控制策略下系统的幅值裕度为14.83 dB，仿真波形如图14所示。

由图13和图14可得，传统并行控制策略和位置环解耦控制策略下系统幅值裕度分别为10.63 dB 与14.83 dB，都略大于理论计算结果，这是因为回差矩阵奇异值等方法的保守性所致，计算结果会比实际值偏小。由仿真波形可以看出，位置环解耦控制策略下系统的稳定性更强，当传统并行控制策略下系统已经开始发散时，仍能够在一定的范围继续保持自身的稳定性。

图13 两种控制策略下回路增益增加3.4倍的 输出力波形Fig.13 Output force waveform with loop gain increased by 3.4 times with two control strategies

图14 两种控制策略下回路增益增加 5.52倍的输出力波形Fig.14 Output force waveform with loop gain increased by 5.52 times with two control strategies

因此，通过两种控制策略下系统的动稳态性能仿真对比可以看出，位置环解耦控制策略下系统的动稳态性能更好，也更加适合直升机主动振动控制这类对系统鲁棒性和抗干扰性具有严格要求的场合。

3 实验验证

3.1 实验平台

为了验证消振电力作动器用位置环解耦控制策略的优良性能和控制系统参数设计的合理性，搭建了实验平台，实验平台包括有消振电力作动器及其电驱动器、测力天平、上位机和输出力信息采集分析系统。实验时，控制器向作动器的电驱系统发送控制指令驱动消振电力作动器执行，测力天平负责实时采集消振电力作动器输出力的加速度信号送至输出力信息采集分析系统，最后将分析得到的力信号送至上位机中拟合。

图15所示为作动器内部结构图。控制驱动板安装在作动器外侧，配重质量块通过紧固螺栓与电机转子连接，磁编电路板通过检测转轴上小磁铁的位置实时获取偏心质量块的相位信息。

图15 作动器内部结构图Fig.15 Internal structure diagram of actuator

实验系统的硬件结构框图如图16所示。电驱模块主要包括控制芯片TMS320F28335、电源电路、采样调理电路、Hall位置采样电路、磁编解码电路、保护电路等，并且负责与上位机之间的通信。偏心质量块的位置信号由绝对式磁编码器测得，电机转速信号由绝对式磁编码器在固定的时间内变化量测得，并送入转速环作为反馈信号。

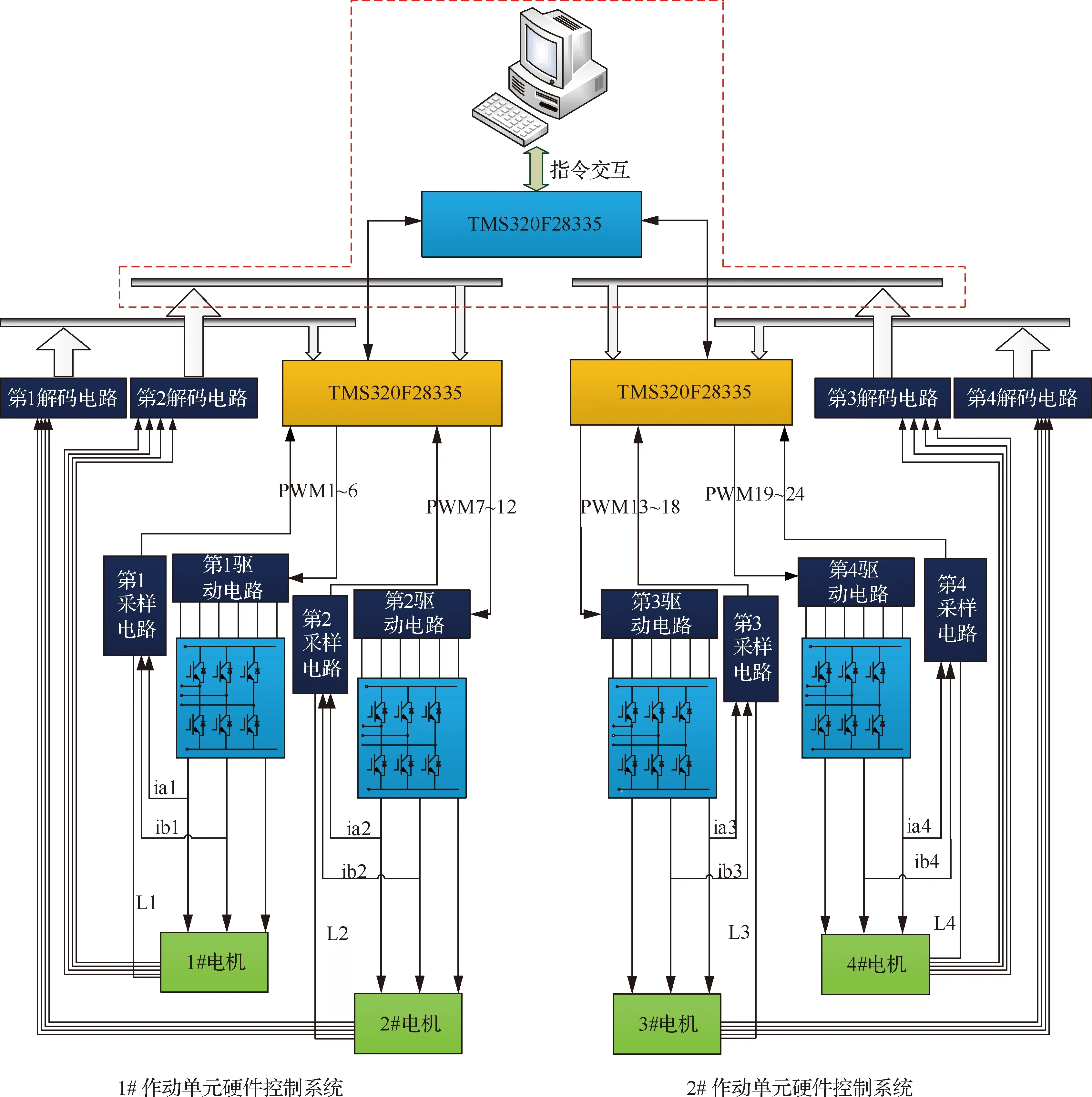
图16 实验系统硬件结构图Fig.16 Experimental system hardware structure diagram

3.2 转速同步性实验

由式(8)可以看出，输出力幅收敛的前提是偏心质量块旋转的频差为零即转速同步，并且频差在零附近波动的范围越小，输出力幅精度就越高。因此给定消振电力作动器工作频率为18 Hz，分别在垂直方向和水平方向进行最大输出力和最小输出力实验，转速差波形如图17所示。当输出垂直最大力时，4台电机的位置始终保持同步，即同时加减速，所以转速差波动也较小。由图17(a)可得，1#和2#偏心质量块、1#和3#偏心质量块的转速差基本稳定在-25～25 r/min；当输出垂直最小力时，相比于输出垂直最大力的情况，最小力时1#和2#偏心质量块的转速差波动变大，这主要是因为针对偏心式负载，当偏心质量块从机械位置最低点转至最高点时，负载转矩对于电机而言为阻力矩，电机减速，而当偏心质量块从最低点转至最高点时，负载转矩变为动力矩，电机加速。当1#和2#偏心质量块的位置差为π rad时，1#偏心质量块加速的同时2#偏心轮减速，因此其转速差相比垂直最大力较大，由图17(b)可得1#和2#偏心质量块、1#和3#偏心质量块的转速差波动范围为-30～30 r/min；当输出水平最大力时，如图17(c)所示，1#和2#偏心质量块的转速差为-25～25 r/min，1#和3#偏心质量块的转速差是-35～35 r/min；图17(d) 表示输出水平最小力时的转速差波形，由于1#和2# 偏心质量块、1#和3#偏心质量块的位置差均为π rad，所以转速差为-35～35 r/min。

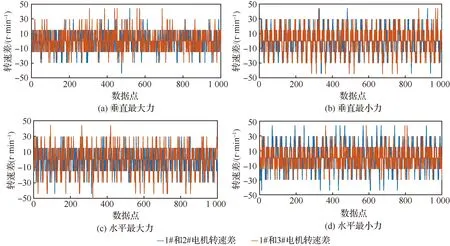
图17 偏心质量块转速差波形Fig.17 Rotational speed difference waveform of eccentric mass

3.3 输出力稳态性能验证实验

为了满足直升机的减振需求，要求在额定频率点24 Hz时输出的最大力不低于3 000 N，同时为了保证控制精度，频率误差要控制在0.5%以内；当输出最小力时，不能产生过大的冲击，图18和图19分别给出了额定工作频率时最大输出力和最小输出力波形。

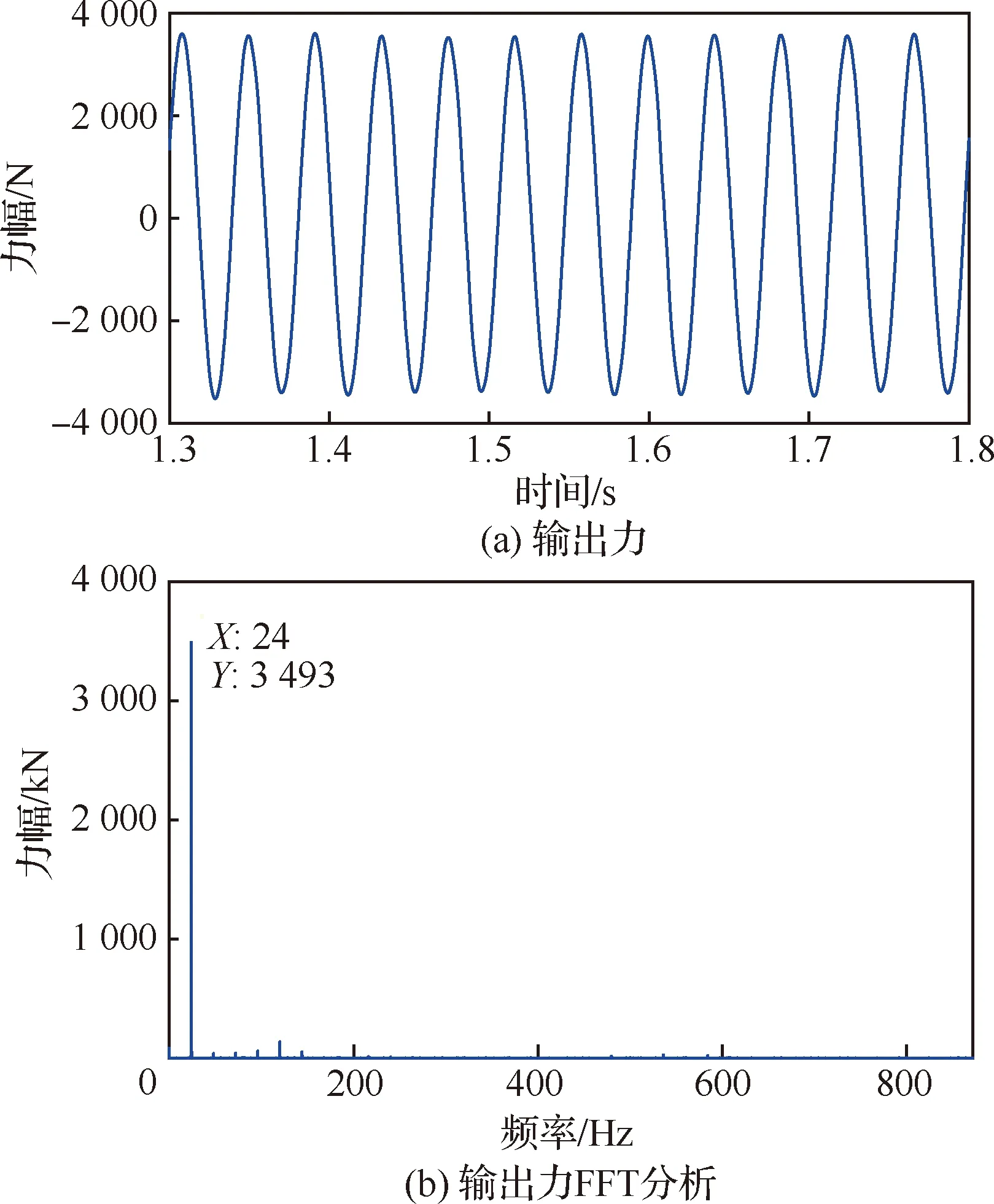
图18 最大输出力波形Fig.18 Maximum output force waveform

图19 最小输出力波形Fig.19 Minimum output force waveform

由图18和图19可得，最大输出力为3 493 N，满足额定工作频率下输出最大力不低于3 000 N的指标要求。对最大力FFT分析可得，实际工作频率24 Hz，与额定频率一致，没有频率误差。同时，输出最小力时，力幅波动-100～100 N，没有产生过大的冲击。因此，可以认为系统具备良好的稳定性能。

3.4 输出力动态性能验证实验

直升机在运行时，如果遇到恶劣天气或是需要进行武装战斗，这都需要积极的调整直升机姿态，因此机体的振动环境也是时变的，这对作动器的动态调节性能提出了极高的要求，指标提出作动器动态调节时间不大于1.2 s。据此，依次发送频率变化1 Hz、幅值变化10%、方向改变30°和相位变化到120°指令，波形如图20～图23所示。

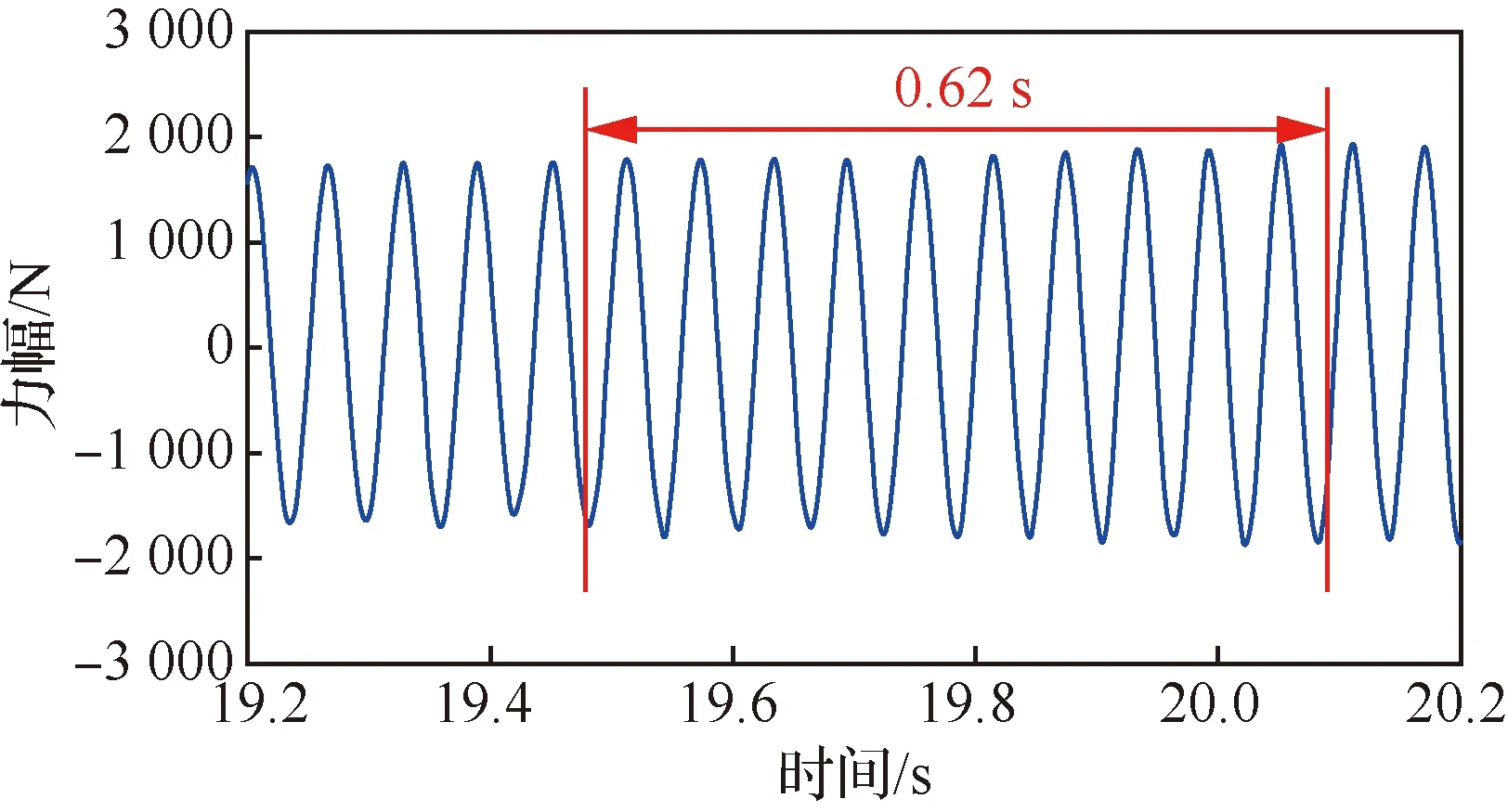
图20 输出力频率变化1 Hz波形Fig.20 Waveform of output force with frequency change of 1 Hz

图21 输出力幅值变化10%波形Fig.21 10% waveform of output force amplitude change

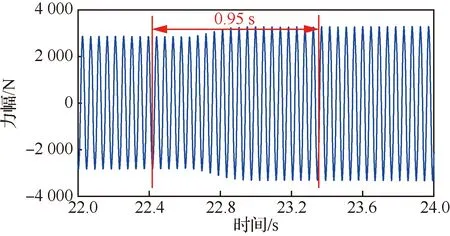
图22 输出力方向变化30°波形Fig.22 Waveform of output force with direction changes of 30°

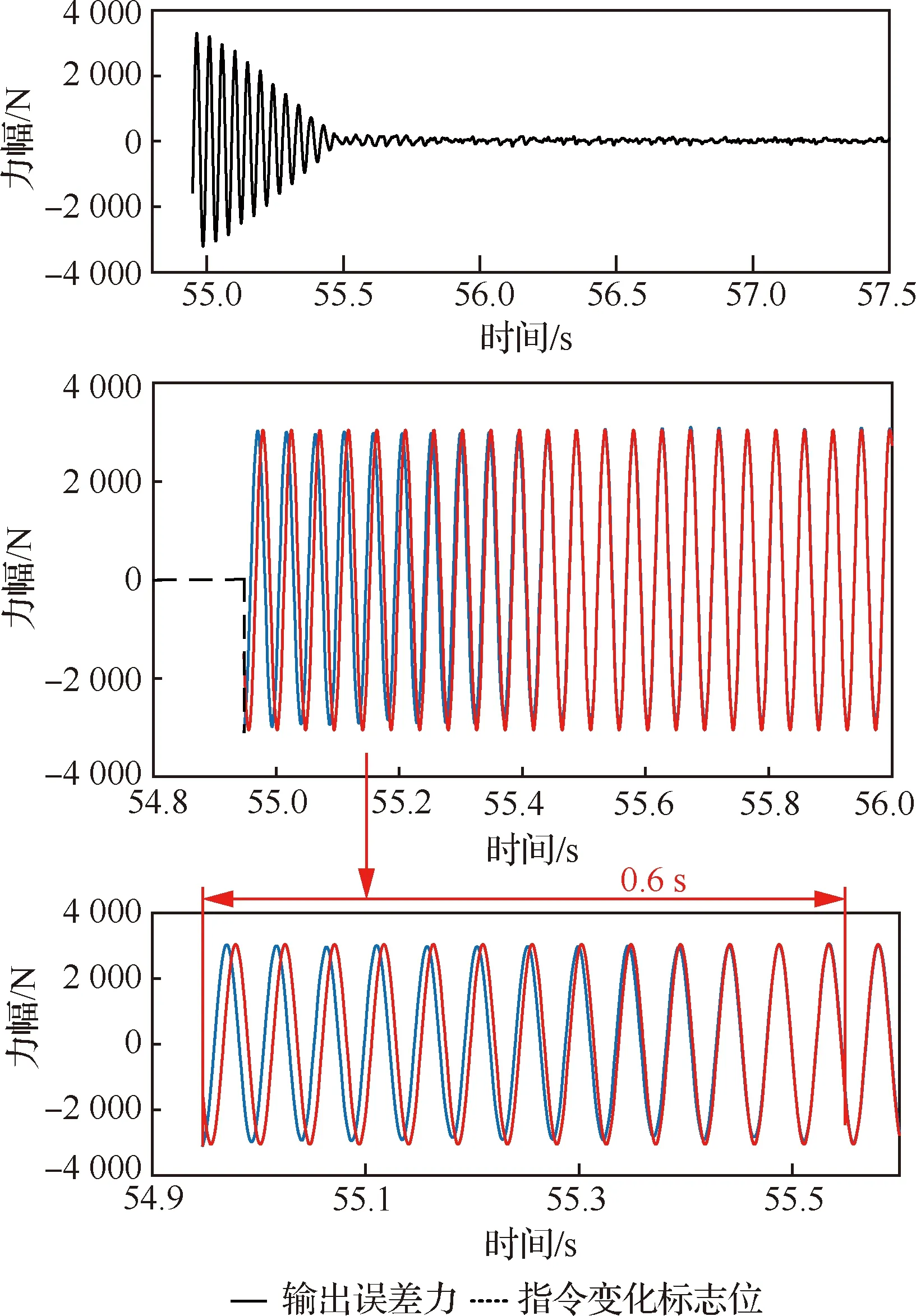
图23 输出力相位变化至120°波形Fig.23 Waveform of output force with phase change to 120°

图20中输出力的频率从16 Hz变化至17 Hz动态调节时间为0.62 s。由式(8)可知，输出力的幅值变化是通过调节作动单元中偏心质量块的相位差来实现的，从而满足不同大小的激振力下的减振需求，由图21可得，输出力从1 800 N变化至2 100 N 动态调节时间为0.57 s。输出力的方向是通过调节不同作动单元中偏心质量块的相位差来实现的，以满足不同方向激振力的减振需求。由图22可得输出力方向变化30°的动态调节时间为0.95 s， 且几乎没有超调。由图23可知，输出力相位变化到120°，实际调整量为48.74°的动态调整时间为0.6 s，稳态相位误差0.2°，实现了给定相位指令的快速准确跟踪。

综上，作动器的实际输出力可以快速跟上给定值，满足指标要求，且稳定后几乎没有稳态误差，控制系统具有良好的动稳态性能，进一步验证了消振电力作动器用位置环解耦控制策略的正确性和位置环参数设计的合理性。

4 结 论

本文研究了直升机用消振电力作动器控制系统，得出如下结论：

1) 提出了消振电力作动器用位置环解耦控制策略，解决了传统并行控制策略带来的系统强耦合问题，便于控制器的参数设计及实现。

2) 建立了两台作动器协调控制的频、相、幅和方向可控的输出力数学模型。

3) 将广义频率法和主导极点法相结合应用于消振电力作动器控制系统的参数设计上，完成了位置环路的PID参数设计。通过回差阵奇异值法等MIMO系统的稳定裕度计算方法计算出系统的稳定裕度，验证了控制策略和参数设计的合理性。

4) 搭建了实验平台，依次完成了转速同步性实验、输出力稳态性能和动态性能验证实验。实验结果表明：电机转速差波动不超过±35 r/min、最大输出力3 493 N、无频率误差、输出最小力冲击不超过±100 N、作动器输出力动态调节时间不超过1.2 s，系统具备良好的动稳态性能，验证了控制策略和参数设计的有效性，为后期的工程应用提供了理论基础。