层流机翼及其增升装置嵌套协同优化方法

罗佳杰，宋文滨

上海交通大学 航空航天学院，上海 200240

燃油成本占当今商用飞机运营成本的很大一部分，减少燃油消耗能节省数百万美元的日常燃油费用，因此提高飞机燃油效率一直是近年来的一个重大挑战。层流机翼技术的应用是降低燃油消耗的一种关键技术，它能大约减阻10%，对应减少5%的燃油消耗。然而，目前使用的后掠翼对前缘附近边界层横流(Crossflow)的增长产生了不利影响，从而大大降低了层流流动的范围，因此对采用跨声速巡航的民航客机而言，高亚声速层流机翼的应用仍然受到限制。为了防止过早出现转捩，机翼前缘后掠角不应大于20°，因此层流机翼的设计巡航马赫数一般不能超过0.75。跨声速层流机翼对机翼的前后缘设计提出了具有自身特点的外形要求，必然影响到增升装置的设计，因此需要在跨声速层流区域和低速增升装置性能之间做出权衡。与传统的分步骤流程相比，一体化的优化设计思路对使用的模型提出了更高精度的要求。

为了能准确预测出转捩位置，需要更高精度的CFD求解器以及合适的湍流模型，其中critical-factors方法和-湍流模型是两种最为常用的用来预测转捩的方法。跨声速层流机翼的气动外形优化要比传统的机翼更为复杂，因为需要同时在层流区域和激波控制之间权衡。对层流有利的顺压梯度往往会导致激波强度增加，而激波增强将对阻力发散和抖振边界产生影响。对于层流翼型和层流机翼的设计和优化，国内外已有不少研究。

与此同时，层流机翼技术对机翼制造提出了挑战，为了实现层流，必须避免机翼上表面出现台阶与缝隙。前缘缝翼通常难以应用在层流机翼上，因为它们在巡航构型时可能存在台阶和间隙导致出现转捩，破坏层流边界层，从而增加摩擦阻力。因此，必须设计新型的增升装置，特别是在前缘，来满足层流机翼的条件。克鲁格襟翼和主动流动控制(Active Flow Control, AFC)是目前国内外研究层流机翼增升装置主要使用的两种技术。对于克鲁格襟翼的设计和优化，国内外亦有不少研究。

尽管克鲁格襟翼能够在保证机翼实现层流的同时提供增升装置的性能，但其效率仍然低于传统的前缘缝翼。因此，层流机翼的设计对后缘襟翼的性能提出了更高的要求，这对于单通道飞机尤为重要，因为与大型宽体客机相比，中短程单通道客机对最大升力系数的要求更高。同时，由于层流机翼的弦长会更小，对增升装置设计指标的压力更大，相比于铰链襟翼(Advanced Drop Hinge Flap)，应该使用气动性能更好的富勒襟翼(Fowler Flap)。富勒襟翼的驱动机构通常是四连杆或连杆滑轨，所以起飞构型能实现小角度偏转和较大的后退量，着陆构型能保证较大后退量的同时实现大角度偏转，因此气动性能更好。而铰链襟翼由于受到机构约束，后退量受到限制，着陆构型虽然也能实现大角度偏转，但是还需要通过扰流板下偏来弥补气动性能上的损失。

以上的研究对于层流机翼或者增升装置的研究是互相独立的，并没有考虑两者之间的融合关系。而跨声速层流机翼对前后缘设计提出了具有自身特点的外形要求，需要考虑两者之间的嵌套协同优化。对于二维翼型和增升装置的协同优化，李高华等已有过研究，但是他们在协同优化时的低速构型并没有直接考虑增升装置的气动，而是在优化翼型的基础上开展增升装置的优化，并且只考虑了前缘缝翼的优化。

与已有的跨声速翼型高低速协同优化研究中通常只考虑压差阻力相比，本项工作的创新点在于同时考虑了跨声速层流机翼优化两个主要目标，一是尽可能保证大范围的层流，以减小摩阻，二是减小激波强度，以减小压差阻力，由此减小总阻力。并且在优化高速构型的同时考虑了低速增升装置的性能。相比传统的高低速松耦合设计方法，本研究使用嵌套协同优化设计方法，可以保证对巡航构型阻力系数和层流区域影响很小的情况下，大幅提升增升装置的性能。

1 嵌套协同优化设计方法

1.1 参数化建模方法

层流机翼及增升装置(HLD)的参数化模型使用CATIA建立，同时使用Visual Basic脚本实现模型的自动化更新和各层级模型之间的关联。巡航构型机翼的参数化建模充分考虑了气动外形建模的要求，同时考虑了各种约束条件和各级参数之间的传递关系，该模型可以直接应用于工程设计，同时也能控制和调整参数，得到较为简单的梯形翼，用于初步设计和研究。考虑到工程应用的机翼较为复杂，本研究使用的研究对象基于梯形翼开展计算、分析和优化。参数化建模方法和典型巡航机翼完全一致，这意味着针对梯形机翼的分析优化结果可以具有直接的借鉴意义。在增升装置的选择上，前缘使用克鲁格襟翼，后缘使用富勒襟翼。

1.1.1 层流机翼参数化模型

参数化模型层级关系如图1所示，平面形状参数定义方法和范围如图2(a)和表1所示，基准值参考了CRM-NLF(Common Research Model with Natural Laminar Flow)中缩比模型的数值。平面形状约束了机翼在平面投影的形状，平面形状参数定义方法如图2(b)和表2所示，它约束了机翼在平面投影的形状。平面形状与组合，最终可以确定机翼的前后缘线的空间形状。

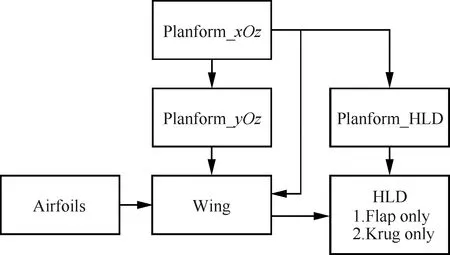
图1 机翼和增升装置参数化模型层级关系图Fig.1 Hierarchy diagram of parametric model of wing and high-lift devices

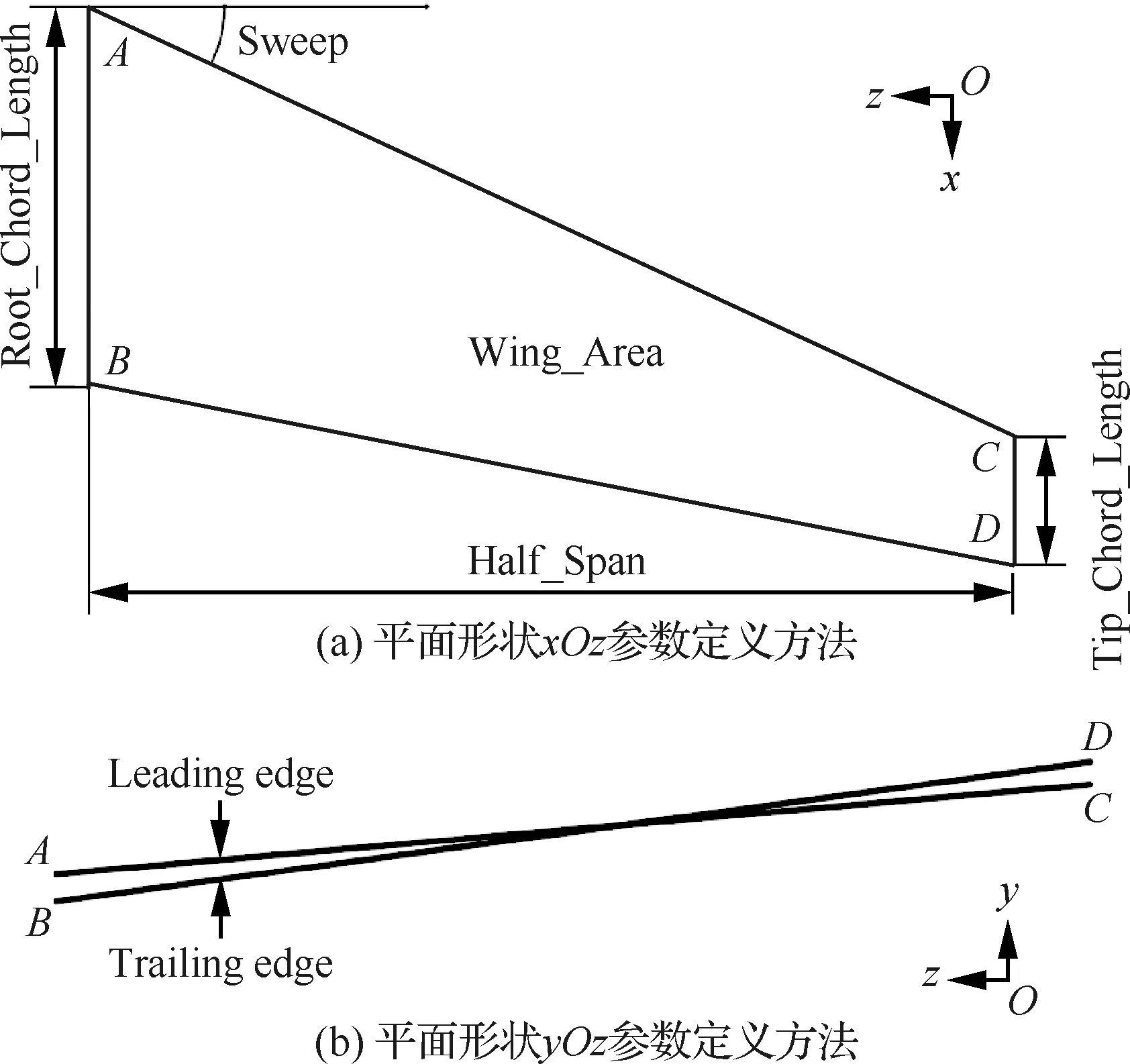
图2 平面形状参数定义方法Fig.2 Definition method of planform parameters

表1 平面形状xOz参数和基准值Table 1 Planform xOz parameters and base values

翼型采用非均匀有理B样条曲线(Non-Uniform Rational B-Splines，NURBS)进行建模，曲线由控制点定义。以上表面曲线为例，参数定义方法和范围如图3和表3所示。上表面曲线由和两段曲线构成，具体来说，曲线由控制点、、、和定义；曲线由控制点、、、和定义。此外，参数_，_，和_固定，可以满足曲线在点和点二阶连续约束条件。这样上表面曲线可变参数一共有11个，下表面曲线定义方法和上表面一致，参数同样为11个，翼型参数总共为22个。考虑到每增加一个翼型截面，参数就会增加22个，对后续优化不利，所以最终使用3个截面翼型进行建模，截面位置分别在翼根、翼尖和37%展长位置。

表2 平面形状yOz参数和基准值Table 2 Planform yOz parameters and base values

图3 翼型上表面曲线控制点定义方法Fig.3 Definition method of control points of airfoil upper surface

表3 翼型上表面曲线参数和范围Table 3 Airfoil upper surface parameters and their ranges

1.1.2 增升装置参数化模型

富勒襟翼外形同样采用NURBS曲线进行建模，如图4(a)所示，曲线由控制点、、、和定义，曲线由控制点、、、和定义。后梁的位置固定在70%弦长位置。共使用12个参数来确定控制点的位置，在表4中给出，并且这些参数都是无量纲化的。图4(b)给出了富勒襟翼缝道的参数定义方法，由此可以确定襟翼的空间位置。

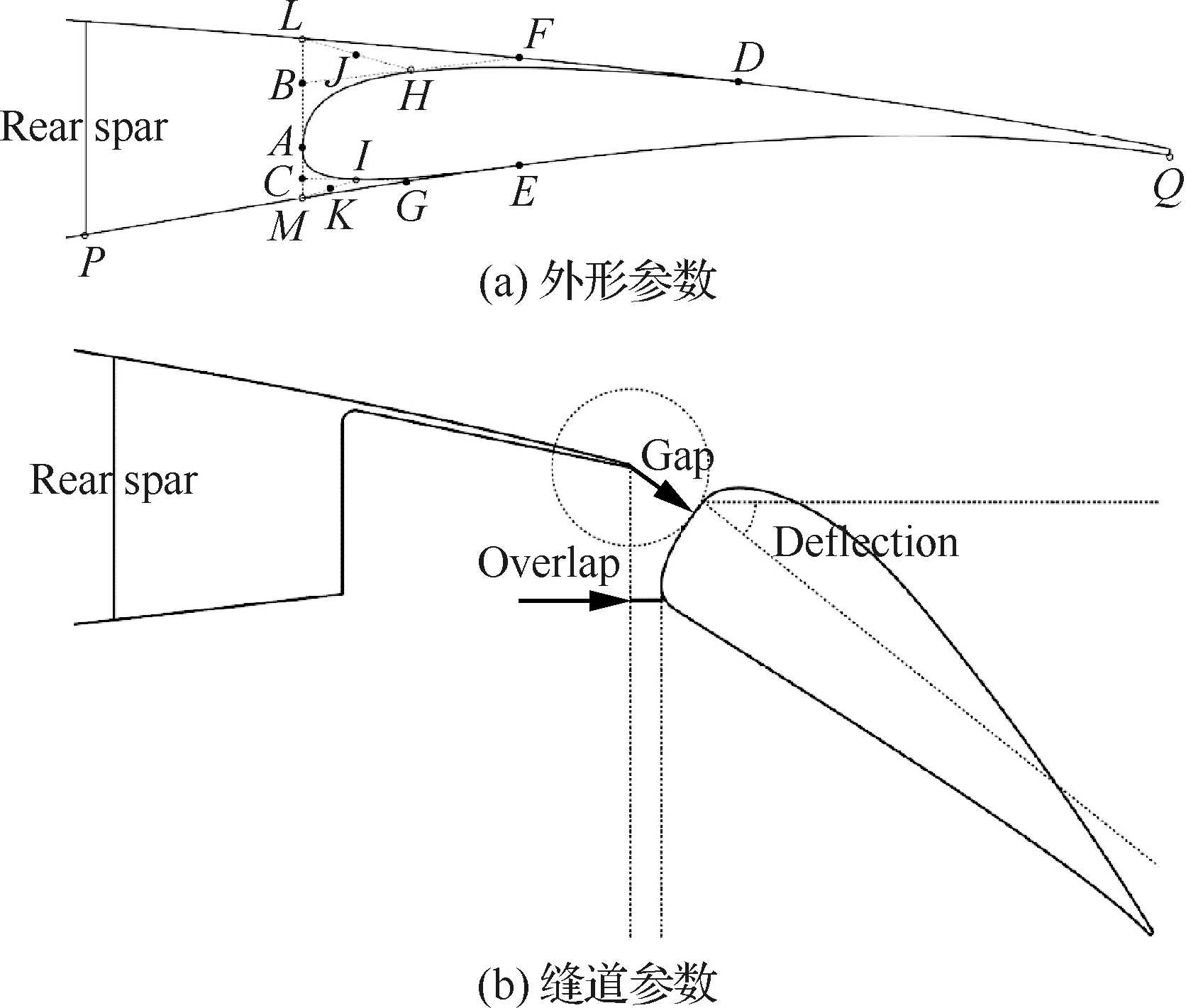
图4 富勒襟翼参数定义方法Fig.4 Fowler flap parameters definition method

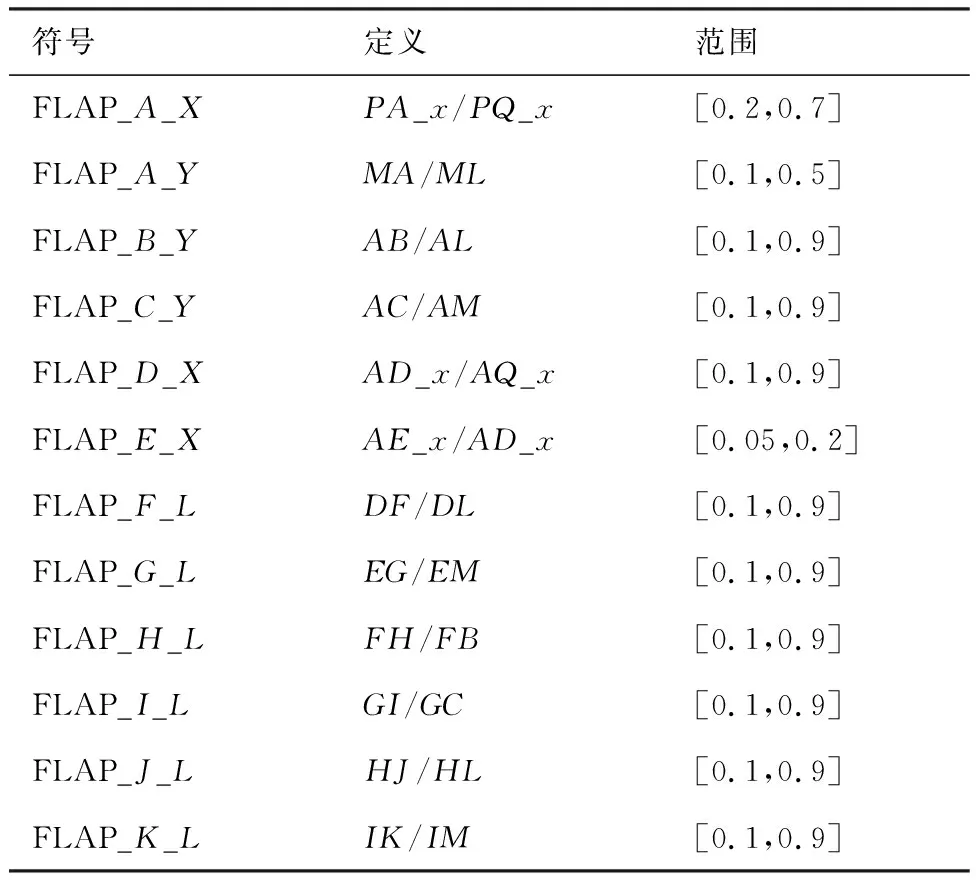
表4 富勒襟翼外形参数和范围Table 4 Fowler flap shape parameters and their ranges

克鲁格襟翼外形如图5(a)所示，前梁的位置固定在20%弦长位置，克鲁格的头部曲线由控制点、、、和定义。此时克鲁格襟翼为完全收起状态，并且头部也是折叠状态，以尽可能减小占用空间。当头部(即)绕点旋转后，与重合，头部为打开状态。表5中给出了参数的定义方法和范围。与富勒襟翼类似，图5(b)给出了克鲁格襟翼缝道参数定义方法，由此可以确定其空间位置。

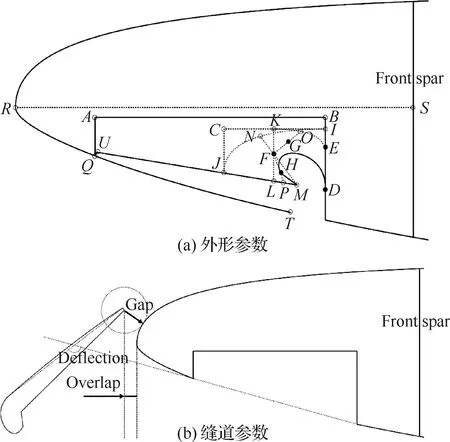
图5 克鲁格襟翼参数定义方法Fig.5 Krueger flap parameters definition method

在给定的展向分布范围内截取多个截面(默认11个截面)，然后在每个截面的翼型上使用和二维增升装置相同的建模方法进行建模，最后使用多截面曲面成型，就可以完成三维增升装置的外形曲面建模。在得到三维增升装置的外形后，富勒襟翼空间位置定义方法如图6所示，核心思想是通过两个截面的缝道参数来确定富勒襟翼的空间位置。首先襟翼沿截面1运动，使该截面的缝道参数符合条件，得到图中襟翼，然后再绕该截面的两个轴线旋转(可以保证该截面的缝道参数不变)，使得截面2的缝道参数满足条件，得到襟翼。克鲁格襟翼空间位置定义方法与之类似。

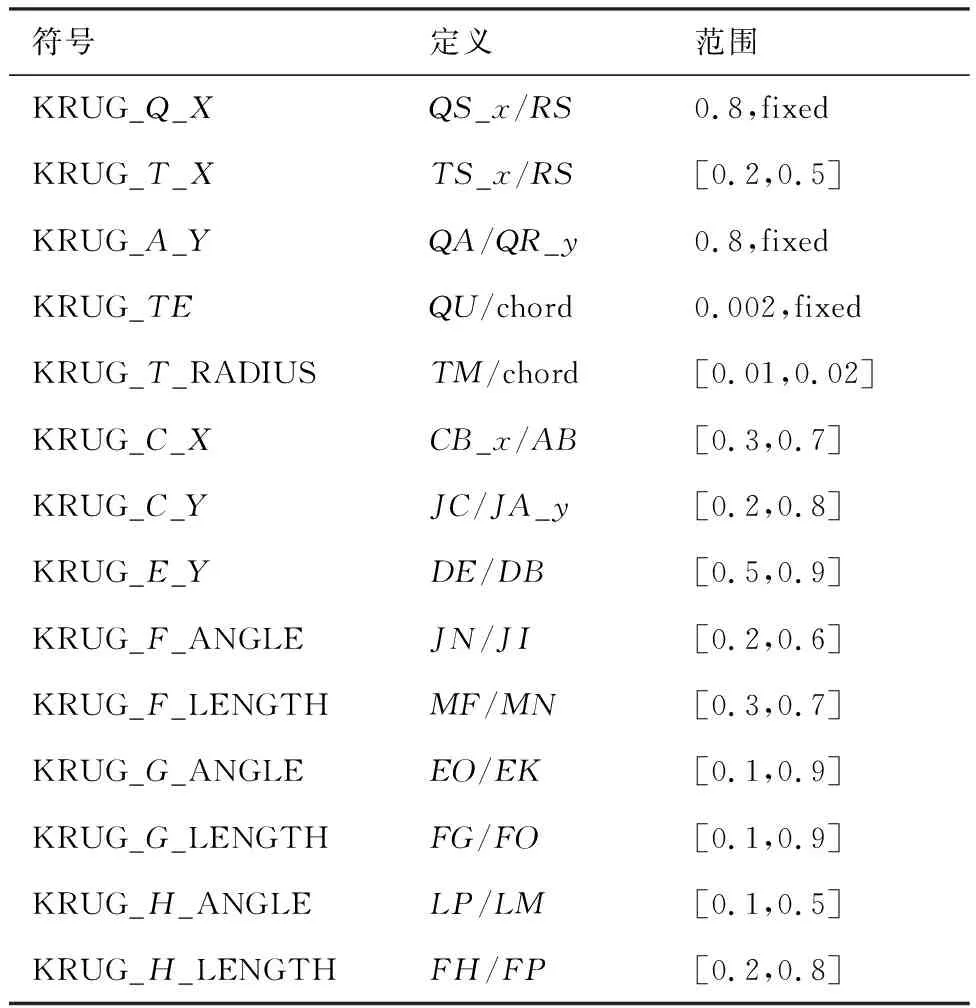
表5 克鲁格襟翼外形参数和范围Table 5 Krueger flap shape parameters and their ranges

图6 富勒襟翼空间位置定义方法Fig.6 Definition of spatial position of Fowler flap

1.2 数值模拟方法

1.2.1 巡航构型

本研究的CFD计算使用CFD++，对于巡航构型，使用-湍流模型进行转捩预测，转捩位置判断的标准为表面摩擦系数突然升高的位置。分别使用NLF(1)-0416层流翼型和CRM-NLF层流机翼进行二维和三维的验证计算。网格如图7所示，二维网格为O型拓扑，网格总数为10 万，远场距离翼型20倍弦长，第一层网格厚度为6×10，保证≈1，网格增长率为1.1，总层数为133。对于三维网格，一共生成了3种不同密度的网格来做网格收敛性分析，网格总数分别为124万(粗网格)、280万(中等网格)和625万(细网格)，网格远场距离模型表面50倍平均弦长，边界层为结构网格，第一层网格厚度为7×10，保证≈1，边界层网格增长率为1.1，总层数为60，边界层到远场之间使用非结构网格填充。二维和三维计算条件分别是马赫数=0.1，雷诺数=4×10，温度=300 K和迎角=1.45°，=0.86，=1.5×10，=277.1 K。

图7 二维和三维标模网格Fig.7 Meshes of 2D and 3D standard models

二维构型0°和不同迎角CFD计算结果和实验结果对比如图8和图9所示，两者匹配较好。图8(a)的表面摩擦系数由于没有实验值，所以和文献[25]中的计算结果对比，由于本文和文献中使用的湍流模型不同，虽然下表面转捩区域的摩擦系数有较大差异，但是本文对下表面转捩点的预测比文献中的更加接近图9(b)中的实验值。不同网格转捩位置和实验结果对比如图10所示，内翼段有点偏差，外翼段和实验结果匹配很好。三维构型不同展向位置截面压力分布计算结果和实验值对比如图11所示。实验中使用温敏涂料来显示层流和湍流区域，由于需要检测温度梯度的变化，使用液氮对来流进行快速降温，这会导致来流条件的改变，同时由于表面瑕疵，例如压力检测孔，风洞中的小颗粒，温敏涂料的损坏，会导致旁路转捩(Bypass Transition)，这些原因都会导致CFD结果和实验之间出现误差。网格收敛性分析如图12所示。升力系数、压力分布和转捩位置的对比都表明，随着网格量增加，结果是收敛的。由于中等网格和细网格的计算结果差别不大，因此在后续优化部分将使用中等网格量，以降低计算成本。

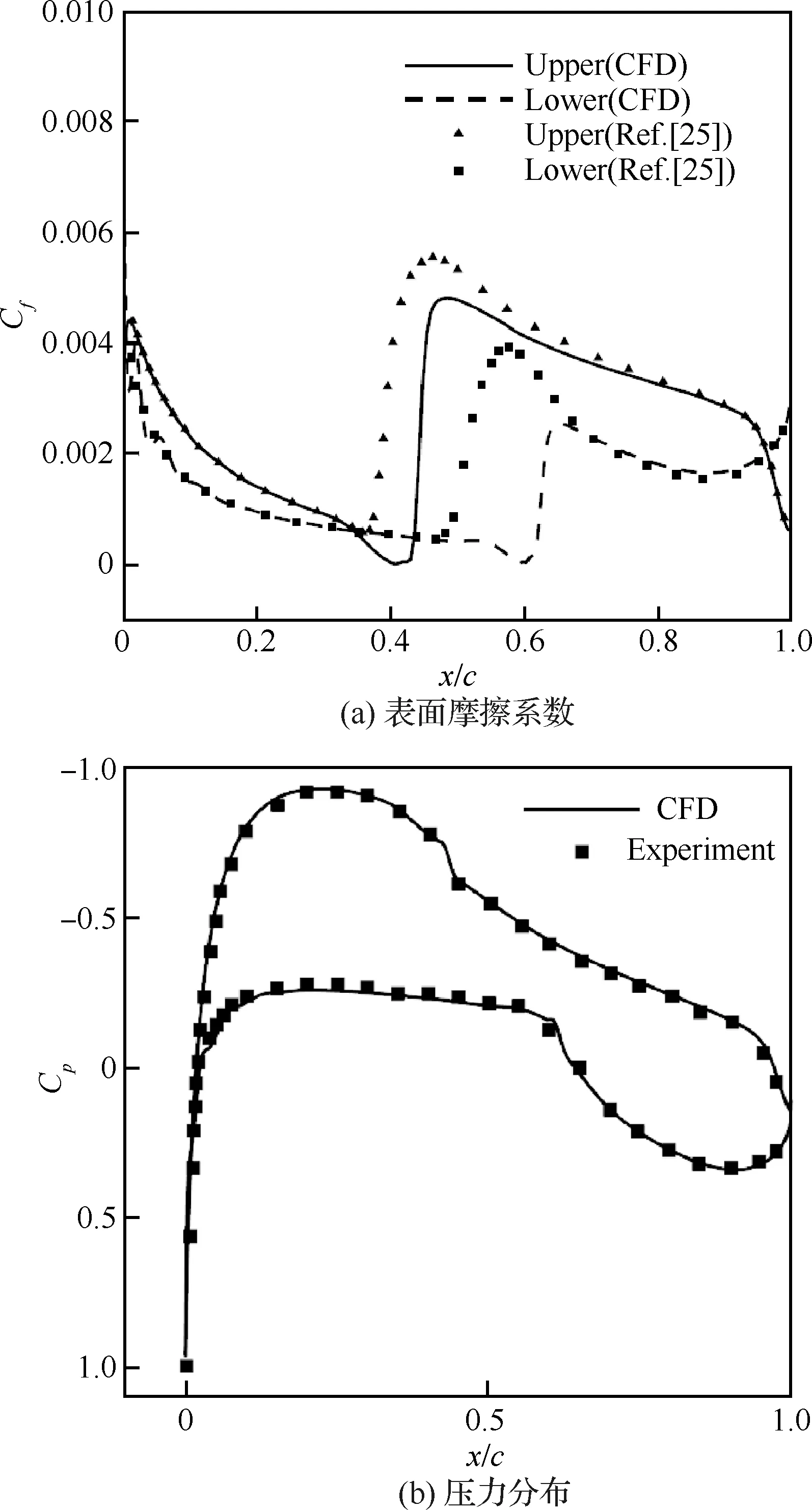
图8 NLF(1)-0416 0°迎角CFD计算结果和实验结果及文献中计算结果对比(Ma=0.1，Re=4×106)Fig.8 Comparison of CFD and experimental and reference results at α=0° of NLF (1)-0416(Ma=0.1，Re=4×106)

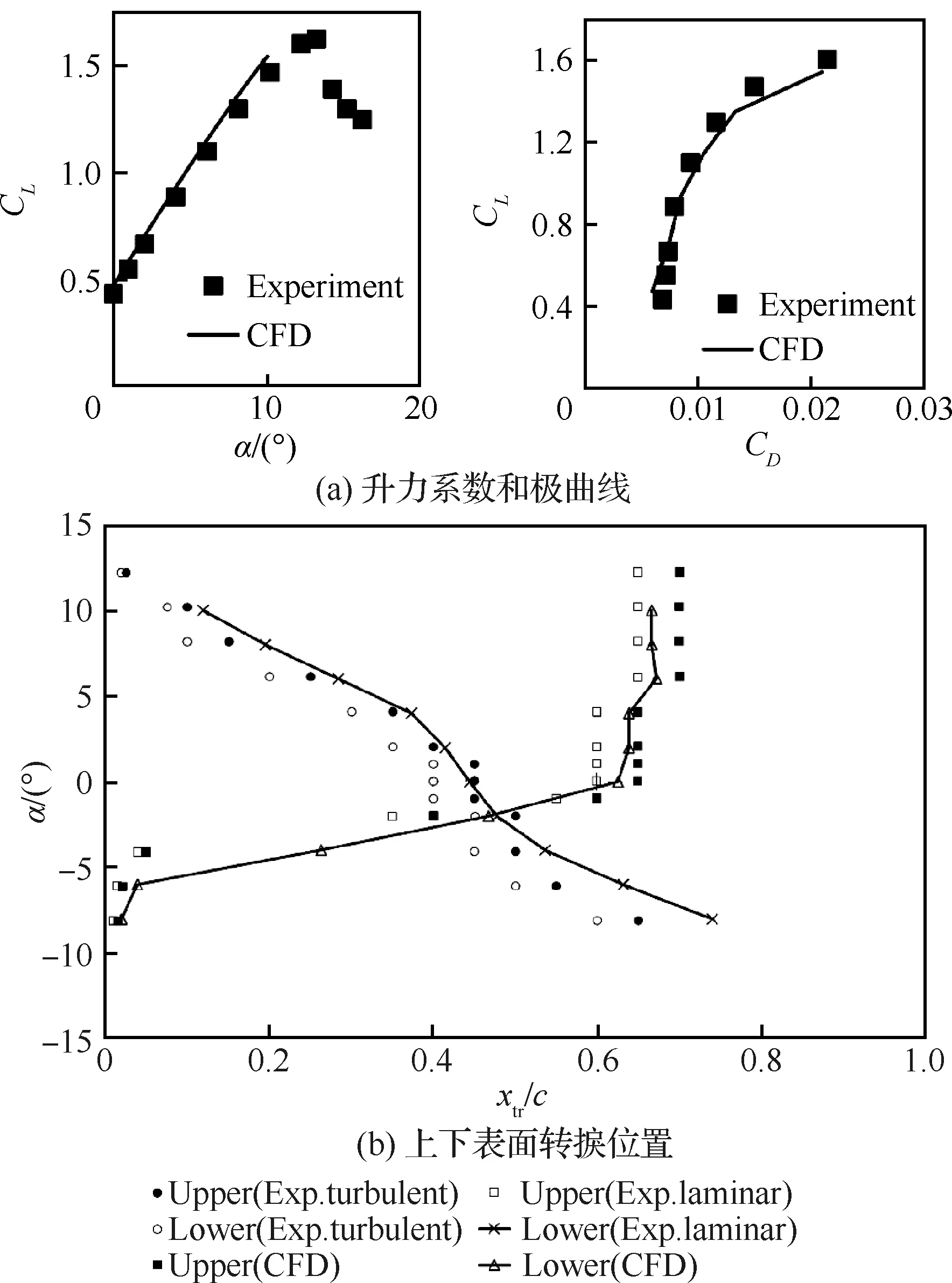
图9 NLF(1)-0416 不同迎角CFD 计算结果和实验结果对比(Ma=0.1，Re=4×106)Fig.9 Comparison of CFD and experimental results at different angles of attack of NLF (1)-0416(Ma=0.1，Re=4×106)

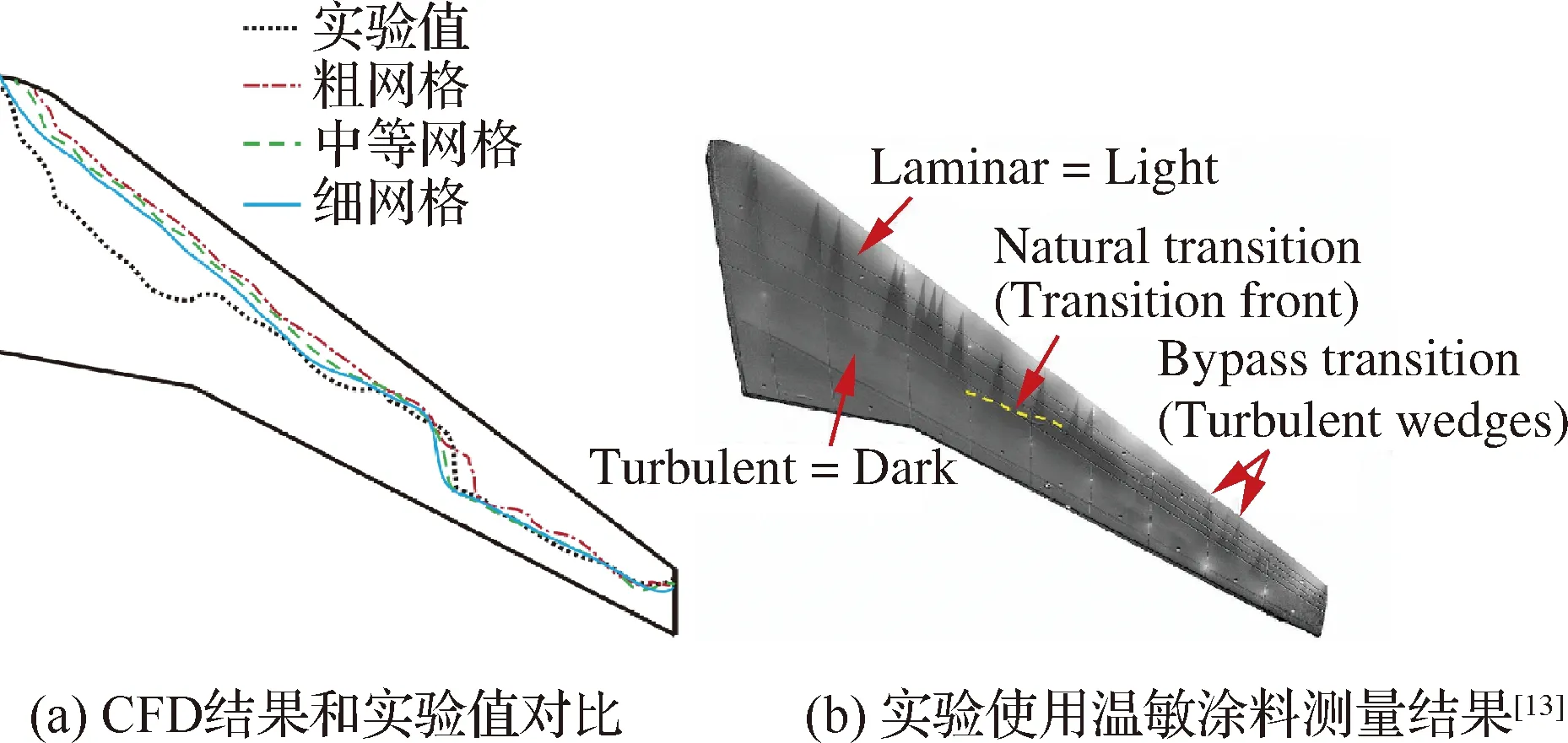
图10 CRM-NLF 不同网格转捩位置和实验结果对比 (α=1.45°，Ma=0.86，Re=1.5×107)Fig.10 Comparison of transition fronts between different grids and experiment results of CRM-NLF(α=1.45°，Ma=0.86，Re=1.5×107)

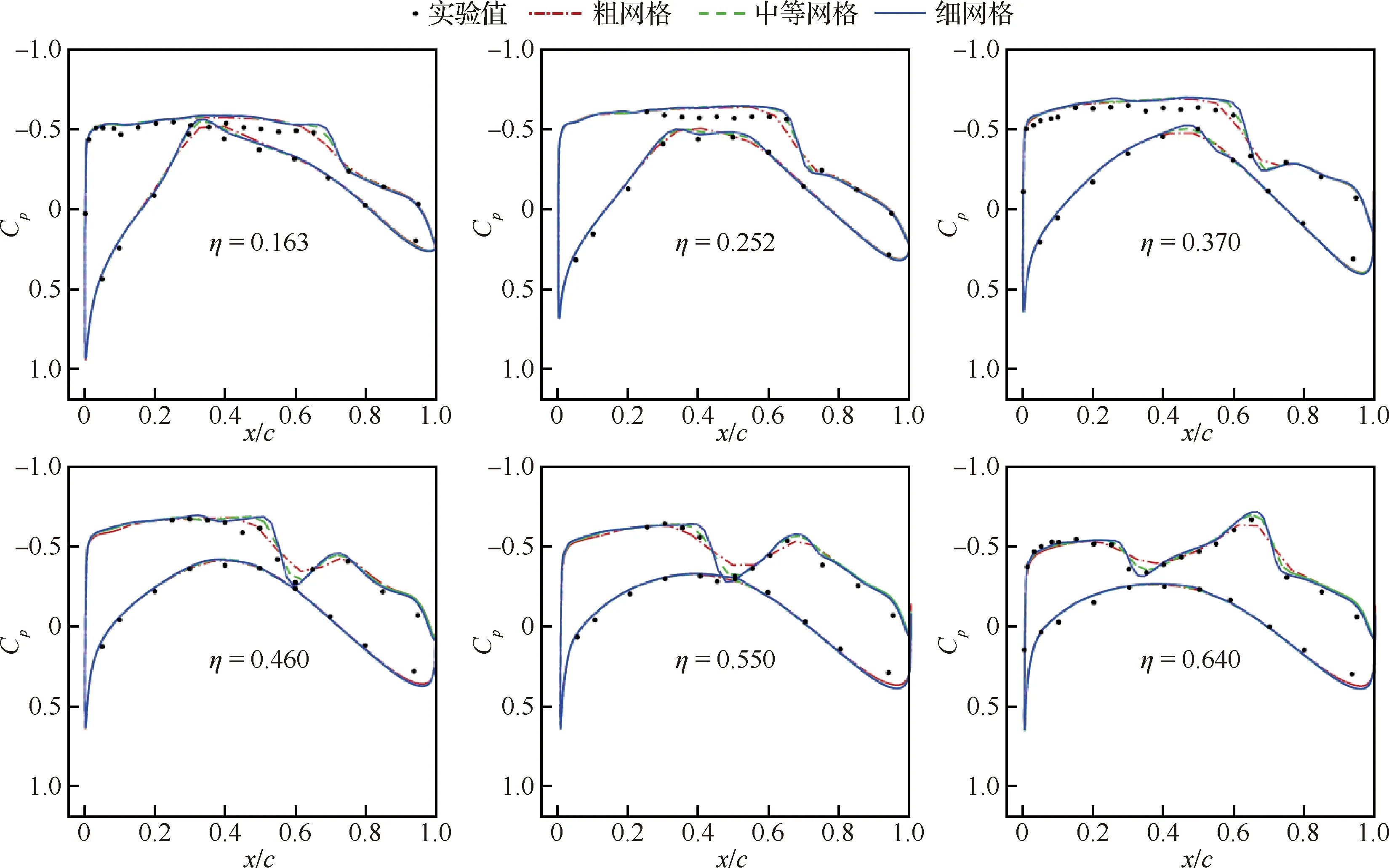
图11 CRM-NLF 不同展向位置截面压力分布计算结果和实验值对比(α=1.45°，Ma=0.86，Re=1.5×107)Fig.11 Comparison of pressure distribution at different spanwise locations with experiment results of CRM-NLF (α=1.45°， Ma=0.86，Re=1.5×107)

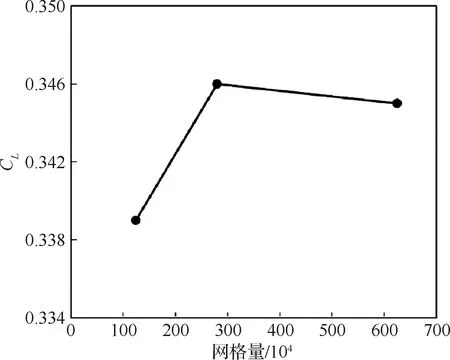
图12 CRM-NLF 网格收敛性分析Fig.12 Grid convergence of CRM-NLF

1.2.2 起降构型

对于起降构型，分别使用L1T2多段翼型和High Lift CRM进行二维和三维的验证计算。网格如图13和图14所示，一共生成了3种不同密度的网格来做网格收敛性分析，边界层为结构网格，第1层网格厚度为1.8×10，保证≈1，边界层网格增长率为1.1，总层数为20，边界层到远场之间使用非结构网格填充。二维网格总数分别为4.1万(粗网格)、15.8万(中等网格)和29万(细网格)，三维网格总数分别为900万(粗网格)、2 400万(中等网格)和5 000万(细网格)。二维和三维计算条件分别是=0.197、=3.52×10、=290 K和=0.2、=3.26×10、=290 K。

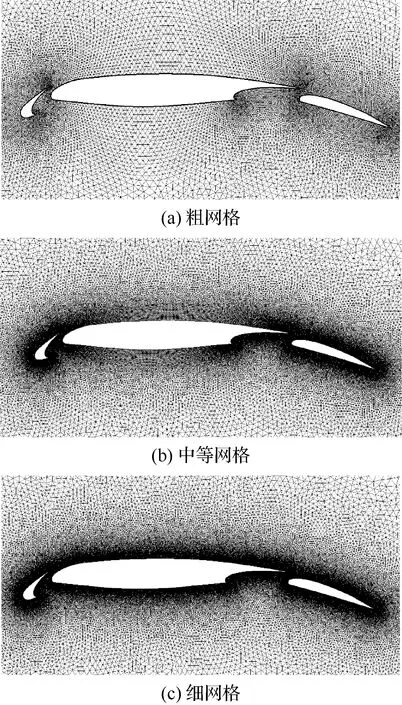
图13 L1T2 不同密度网格Fig.13 L1T2 grid with different density

图14 High lift CRM 细网格Fig.14 Fine grid of high lift CRM

然后使用了两种湍流模型SA和-SST进行比较，如图15和图16所示。对于网格量来说，两种不同湍流模型的结果都表明，随着网格量增加结果是收敛的。对于二维构型，由于中等网格和细网格的计算结果基本相同，因此在后续的二维计算部分将使用中等网格，以降低计算成本，-SST在、失速迎角和压力分布的预测上都比SA更好，因此选择-SST作为湍流模型。对于三维构型，网格收敛性分析如图17所示，随着网格量增加，升力系数是收敛的。在后续的三维计算部分将使用结果最好的细网格SA湍流模型。

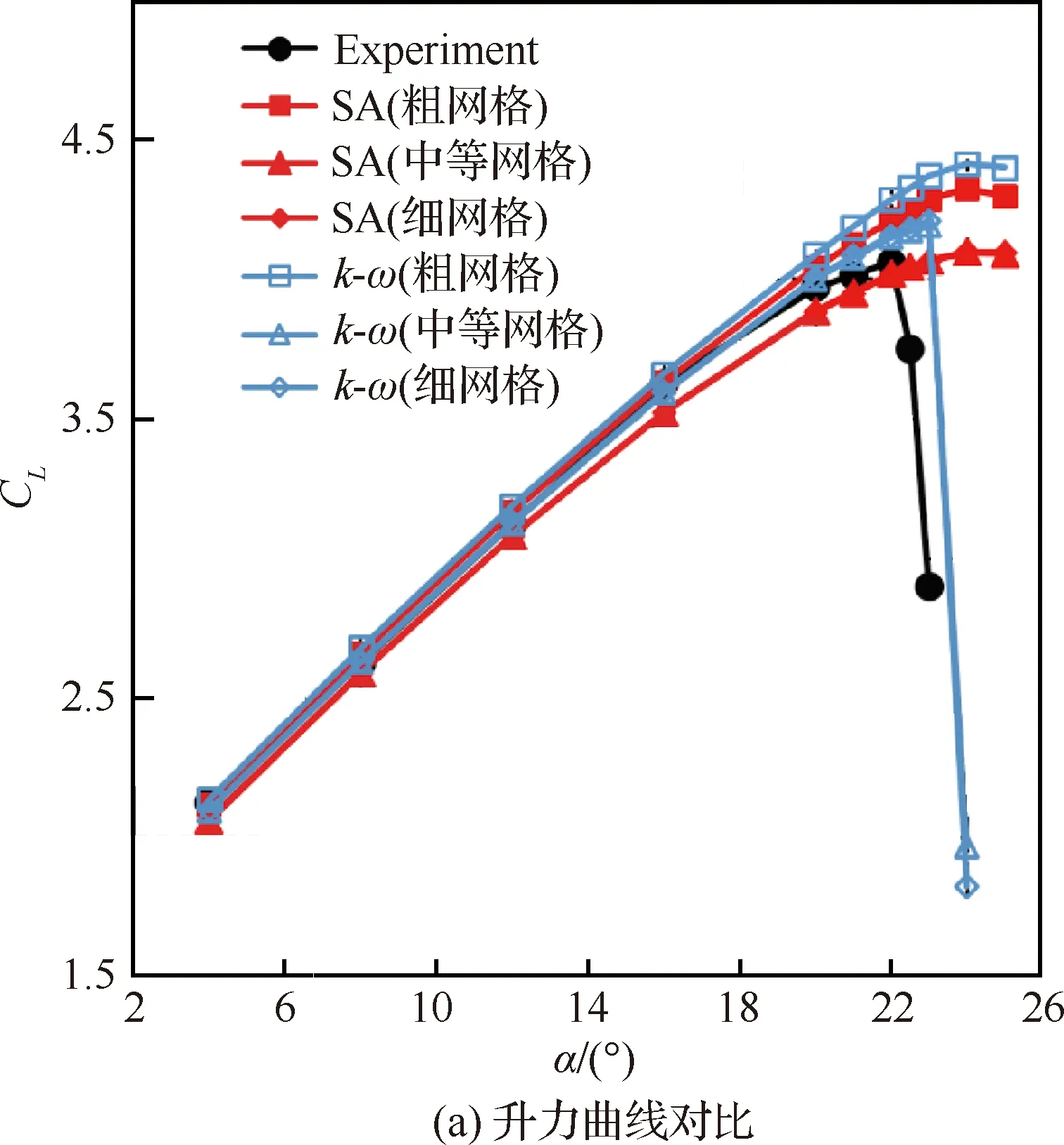
图15 L1T2不同湍流模型和网格量计算结果和 实验值对比Fig.15 Comparison between different turbulence models with different grids and experiment results of L1T2

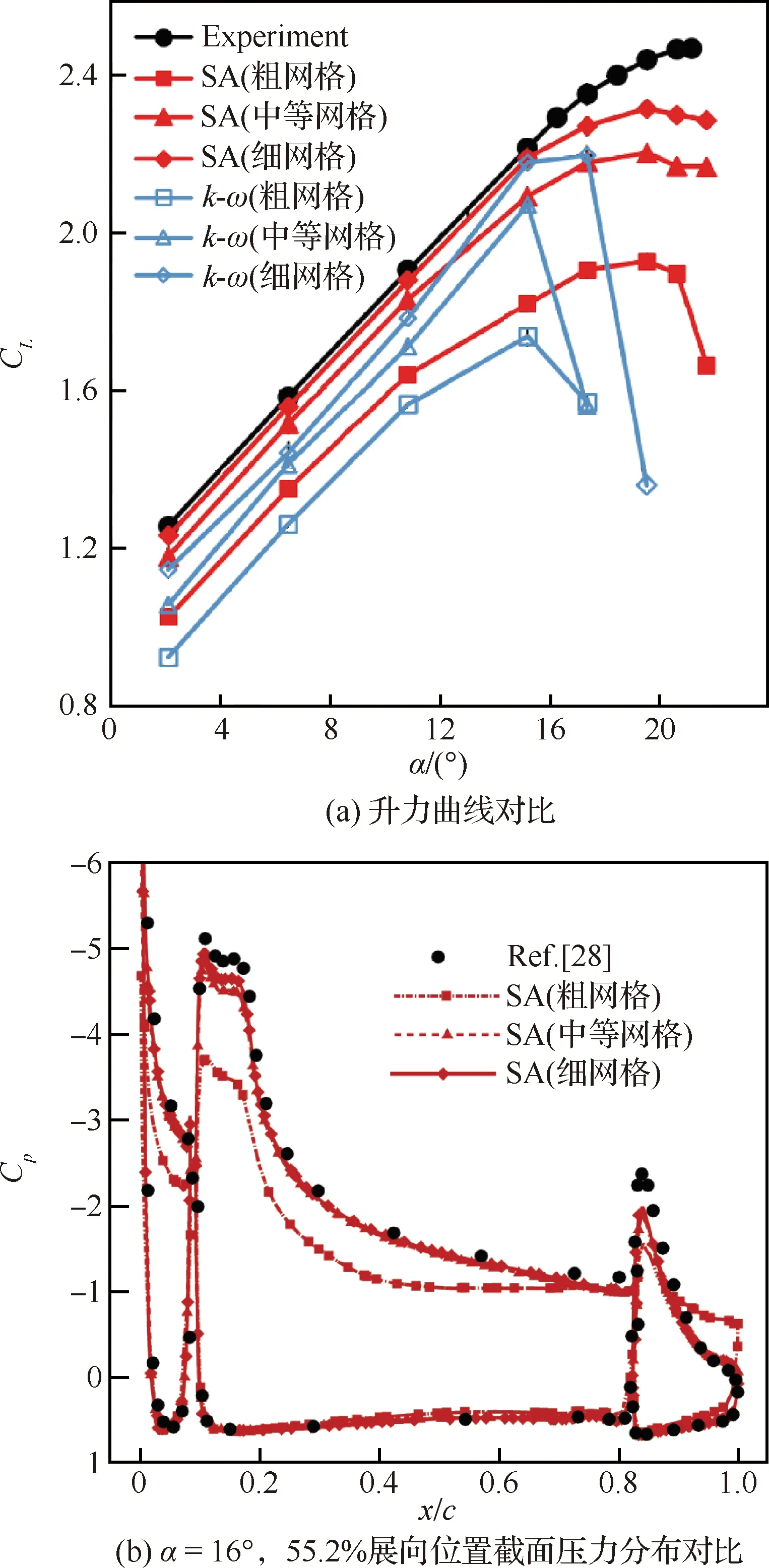
图16 High lift CRM 不同湍流模型和网格量计算结果和文献[28]中计算值对比Fig.16 Comparison between different turbulence models with different grids and those in Ref.[28] of high lift CRM

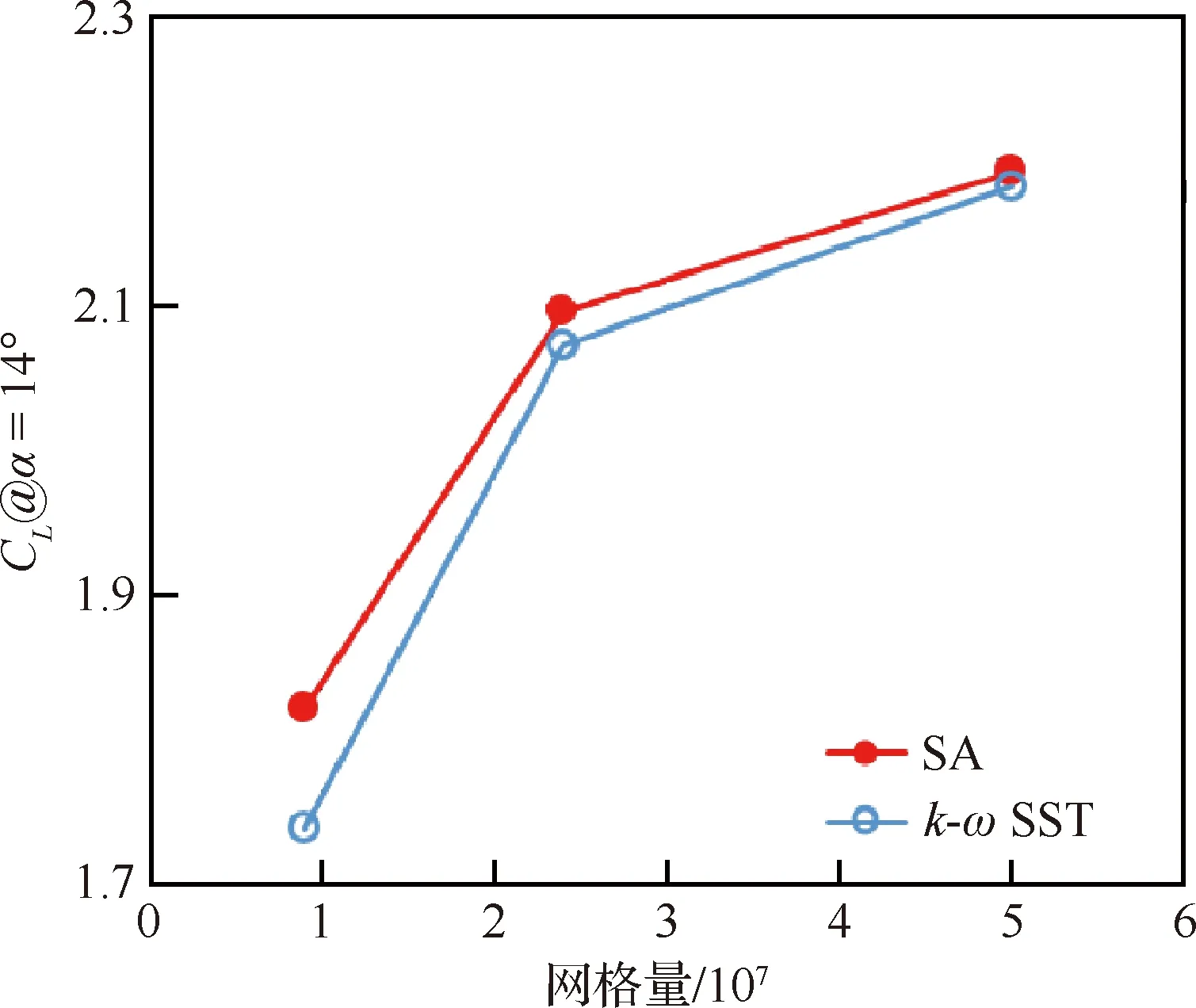
图17 High lift CRM 网格收敛性分析Fig.17 Grid convergence of high lift CRM

1.3 优化流程

嵌套协同优化流程图如图18所示，首先针对翼型开展单目标优化。跨声速层流机翼优化需要考虑两个主要目标，一是尽可能保证大范围的层流，以减小摩阻，二是减小激波强度，以减小压差阻力，由此减小总阻力，只要在层流范围和激波强度之间找到一个良好的权衡，总阻力就应该接近全局最小值，因此，仍然可以直接将总阻力作为优化目标来考虑。本文采用一个相对简单的方法，将CFD++计算得到的总阻力分解为黏性项，即摩阻和非黏性项，以反映压差阻力变化。优化方法使用基于代理模型的遗传算法优化，基准翼型使用CRM-NLF的37%展向位置截面的翼型，并通过转换关系得到对应的二维翼型。然后以优化得到的翼型为基准，开展翼型及增升装置嵌套协同优化。

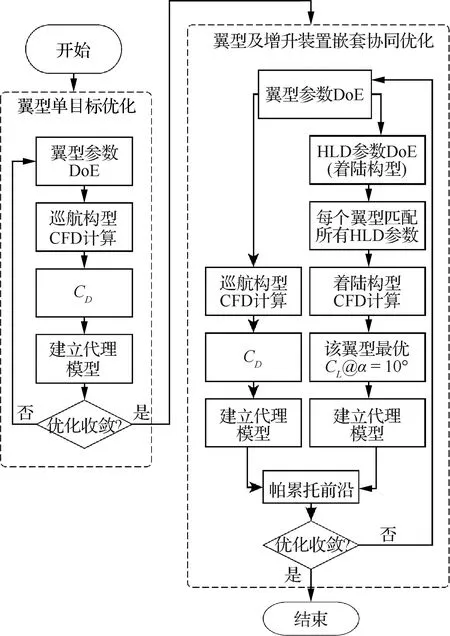
图18 基于代理模型的多目标嵌套协同优化流程图Fig.18 Flow chart of surrogate-based multi-objective nested collaborative optimization

嵌套协同优化问题定义如下:

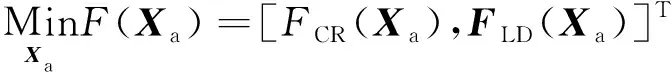
s.t08()≤()≤12()

式中:

()=@Cruise

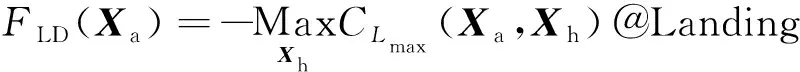
其中：为翼型相对厚度;C()和()为两个优化目标，为22个翼型参数；在多目标优化问题定义内，()为单目标优化问题；为13个增升装置参数，包含7个外形参数和6个缝道参数。

这里定义的嵌套协同优化问题与传统的多目标优化问题不同，传统的多目标优化问题的优化目标通常是一个函数，而嵌套协同优化中()本身是一个单目标优化问题。对于帕累托前沿上的某个点，它的巡航构型和着陆构型的翼型参数是相同的，而对于着陆构型会去优化对应的增升装置参数，来得到最优，对于帕累托前沿上的另一个点，翼型参数发生了变化，因此需要针对此翼型参数重新优化增升装置参数，来得到最优，与此同时，翼型参数也在优化来得到帕累托前沿。因此嵌套协同优化问题比传统的多目标优化问题更加复杂，由于需要计算一系列迎角才能得到，会成倍增加计算量，所以可以计算靠近失速迎角的来代替，失速迎角的范围通过计算小部分样本点来得到，在10°附近。巡航和着陆构型计算条件在表6中给出。

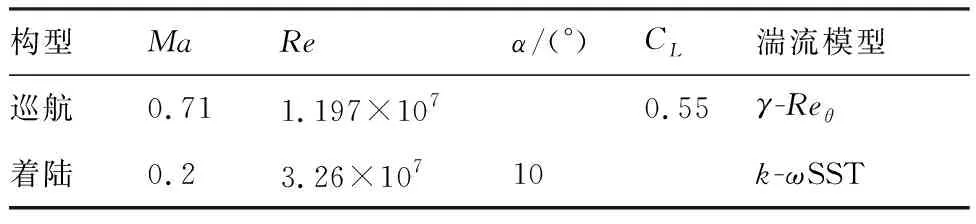
表6 计算条件Table 6 Calculation conditions

2 层流翼型和增升装置嵌套协同优化

2.1 翼型单目标优化

图19(a)显示了经过CFD计算验证的随迭代收敛情况。所有样本点压差阻力和摩阻分解结果如图19(b)所示，压差阻力摩阻和总阻力最小点压力分布、摩阻系数和转捩位置对比如图20所示，翼型对比如图21所示，这些结果很好的反映了压差阻力和摩阻之间的对抗关系。压差阻力最小的翼型上表面更薄，所以激波强度更小，但是顺压梯度减小，导致转捩位置靠前，增加摩阻；而摩阻最小的翼型上表面更厚，顺压区域增加，有最大的层流区域，但是激波强度明显增加，导致压差阻力增加；总阻力最小的翼型在层流范围和激波强度之间找到了一个良好的平衡。

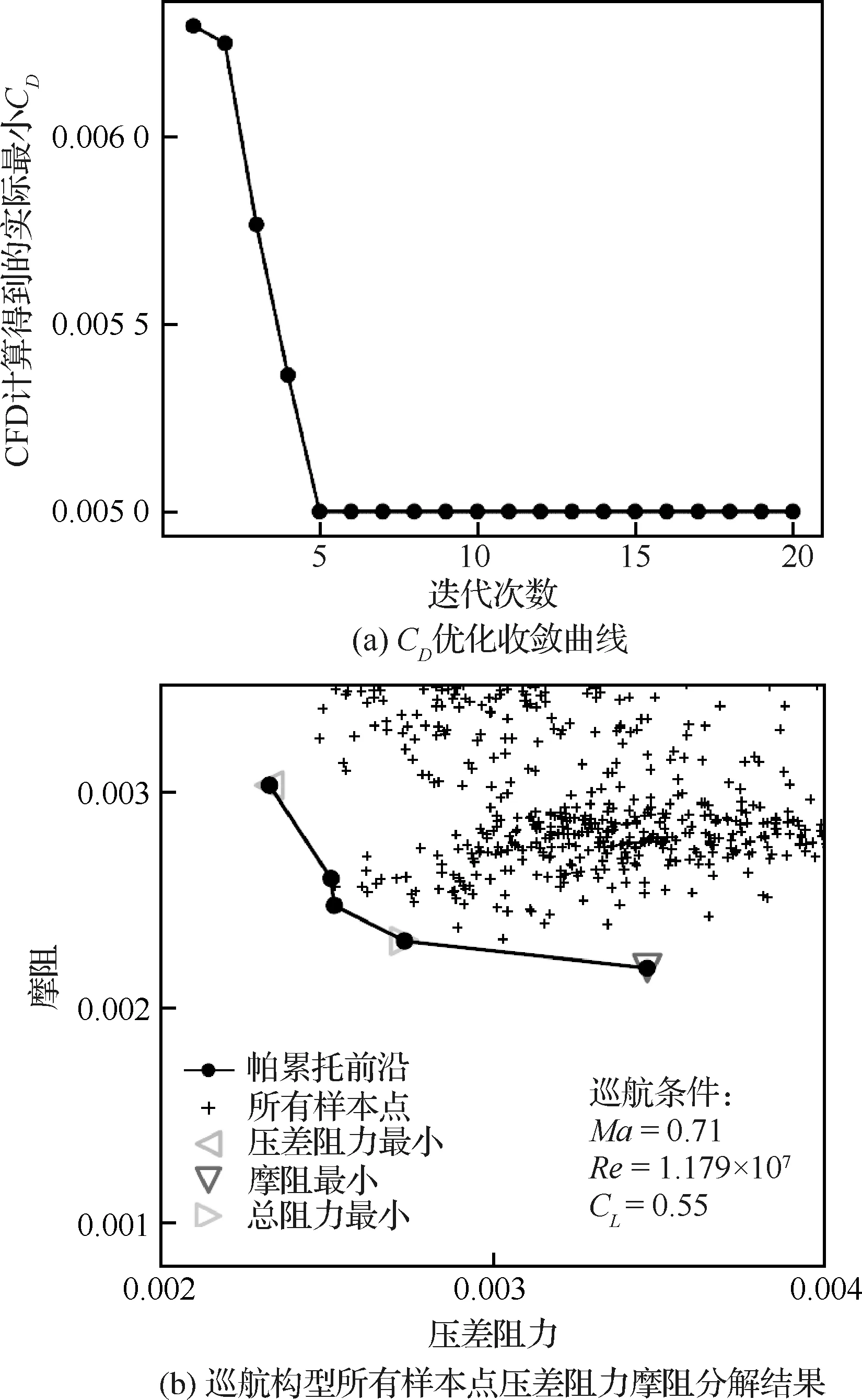
图19 翼型单目标优化结果Fig.19 Airfoil single-objective optimization results

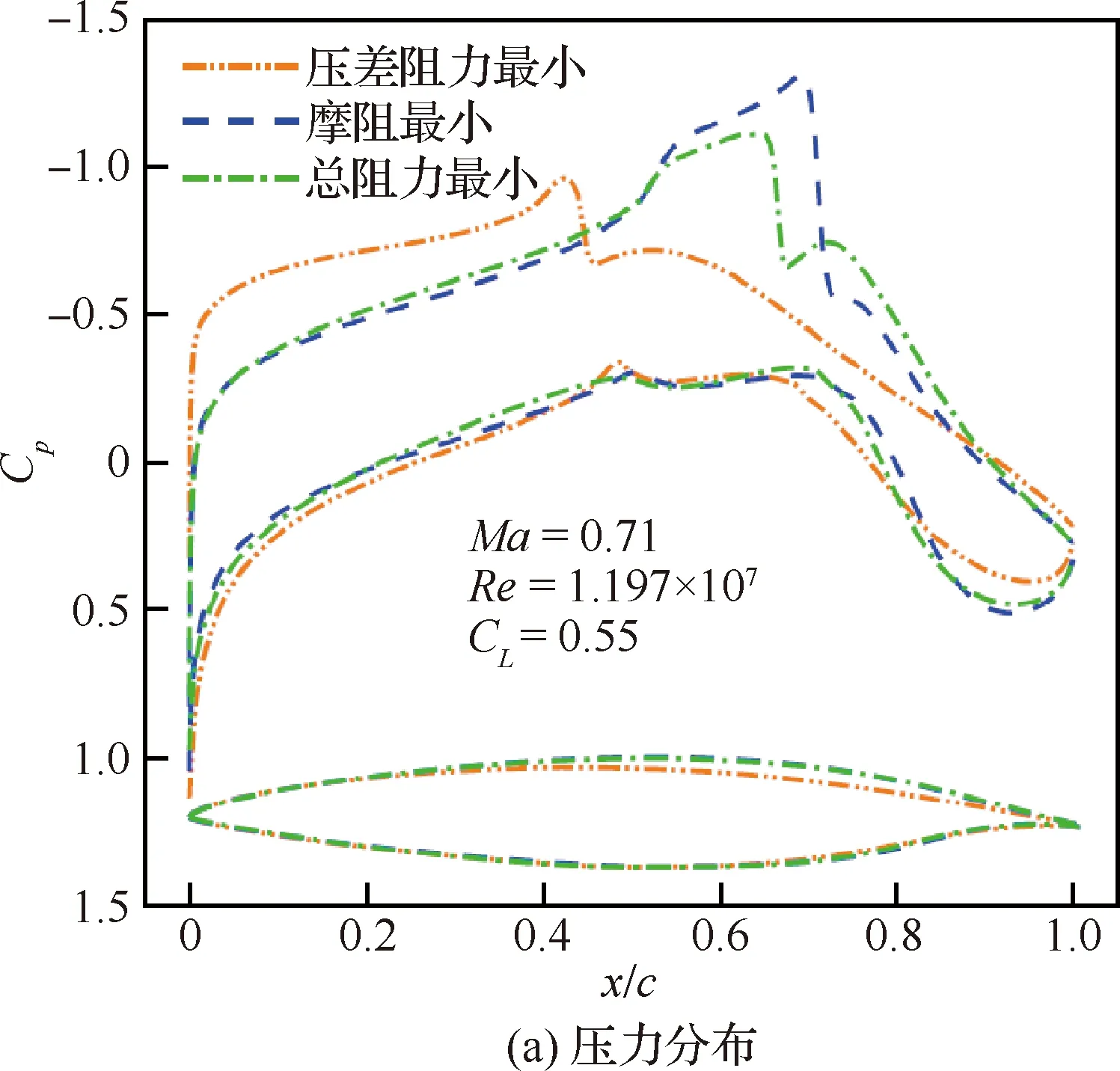
图20 3种单目标(压差阻力、摩阻和总阻力最小点)巡航构型对比Fig.20 Comparison of three single-objective optimization cruise configurations (minimum pressure drag, friction drag and total drag)

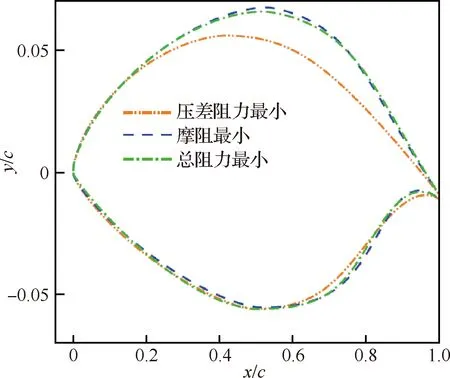
图21 3种单目标(压差阻力、摩阻和总阻力最小点)翼型对比Fig.21 Comparison of three single-objective optimization airfoils (minimum pressure drag, friction drag and total drag)

2.2 嵌套协同优化结果

针对翼型的单目标优化已经得到了一个不错的上表面压力分布和层流区域，虽然下表面层流区域也较大，但是由于前缘下表面有克鲁格增升装置，实际情况中在下表面是无法实现层流的。因此在翼型和增升装置嵌套协同优化时，上表面曲线外形固定，只改变下表面曲线外形，这样可以在优化时保证对上表面压力分布和层流区域影响最小。

嵌套协同优化得到的帕累托前沿如图22所示，其中图22(b)将横坐标转换成上表面转捩位置，‘加权最优’为给两个目标相同的权重系数得到的点，的约束计算如下，使用典型宽体飞机A350-900的参数进行计算，其最大着陆重量为2.07×10kg，机翼面积为440 m，着陆时=0.2，因此，着陆时所需的升力系数为=155，=123×=234(系数1.23参考适航要求)，最后通过转换关系转换成二维构型数值，这为最大升力系数提供了一个近似的最小参考值，并且为从优化结果中选择最终设计提供了约束。3个较优点的值在表7中给出。

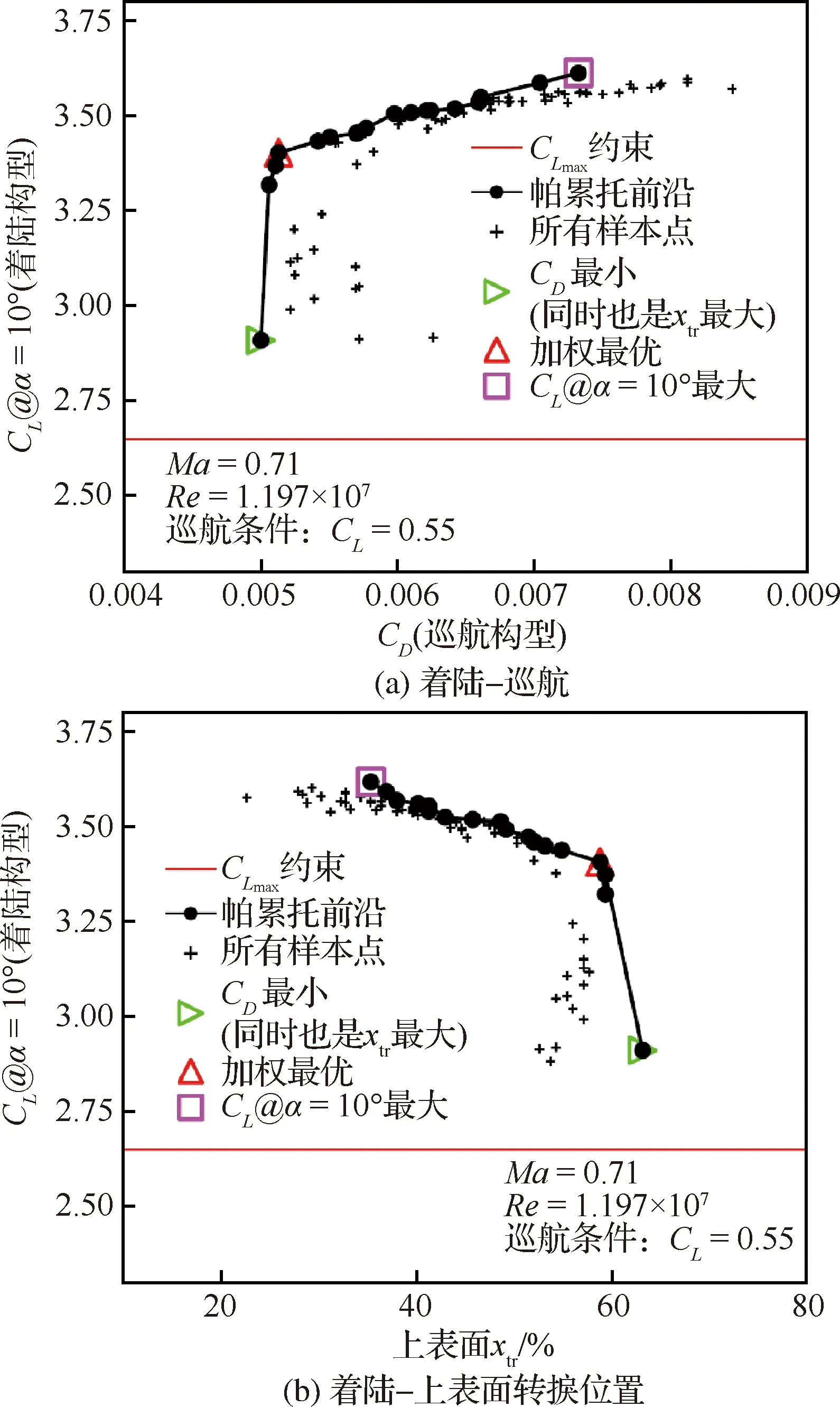
图22 嵌套协同优化得到的帕累托前沿Fig.22 Pareto front of nested collaborative optimization

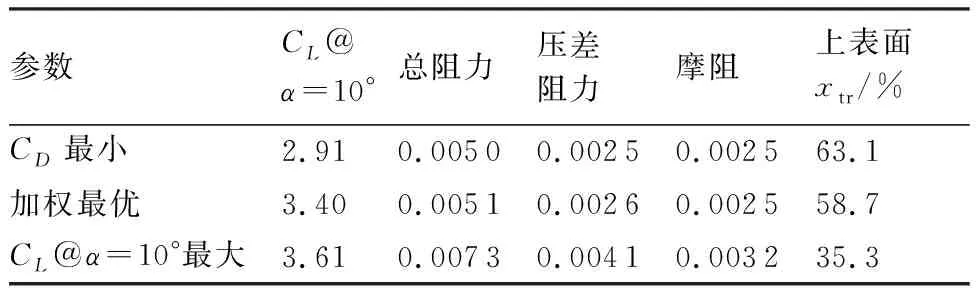
表7 嵌套协同优化得到的帕累托前沿上3个较优点的值

使用传统的先针对巡航构型阻力系数优化翼型，再针对着陆构型升力系数优化增升装置外形和缝道参数的方法只能得到‘最小’点。本文使用多目标嵌套协同优化的优势在于可以得到同时兼顾巡航和着陆构型性能的帕累托前沿上的一系列的点。‘加权最优’相比‘最小’兼顾了着陆构型性能，翼型前缘半径增加了，因此最优的增升装置外形和缝道参数也随之发生了变化，两者耦合，大幅提升了着陆构型的性能，而对巡航构型的性能影响很小，其中着陆构型10°迎角升力系数提升了16.8%，而巡航构型阻力系数只增加了2%，上表面转捩位置只前移了4.4%。从‘加权最优’到‘@=10°最大’之间开始，着陆构型性能提升有限，而巡航构型的阻力系数大幅增加，并且上表面转捩位置明显前移。因此通过嵌套协同优化来找到对巡航构型性能影响不大，但是对着陆构型性能提升明显的翼型是非常重要的。

3个较优点的克鲁格襟翼缝道参数响应面如图23所示，在画响应面时，克鲁格襟翼外形和偏角使用对应的前缘半径的最优参数值。该响应面可以更加直观的反映出翼型前缘半径和缝道参数之间是耦合的。前缘半径改变后，缝道参数响应面的分布规律是不同的，最优的外形和缝道参数也会随之发生变化，需要针对该前缘半径来优化得到最优的外形和缝道参数，因此开展嵌套协同优化是非常重要的。

虽然协同优化所需要的样本点比采用先优化翼型再优化增升装置的方法多2个数量级，以目前高性能计算机的算力(本研究使用2.5 GHz Intel Xeon CPU)，计算量是可以接受的。本研究计算1个样本点使用1个CPU核的时钟时间为1 h，所有样本可以并行计算。使用120核，计算所有10 000个 样本点所需要的时钟时间为3.5 d。这在工程上是可以接受的，并且如果使用更多CPU核，计算时间可以进一步减少。

3个较优点压力分布，摩阻系数和转捩位置对比如图24所示，翼型对比如图25所示，随着翼型前缘曲率半径增加，着陆构型性能提升，但是超过某个临界值后会对巡航构型上表面压力分布产生较大影响，使层流区域大幅减小。图26展示代理模型响应面。在本节的优化中，只使用对翼型下表面曲线外形影响最大的4个方向参数，在画响应面时，任选2个参数，剩下的参数默认固定为参数范围的中间值，这样两两组合，对于每个目标函数一共可以得到6个响应面。这些响应面很好的反映了翼型前缘曲率半径对于3个目标函数的影响趋势，其中参数_为下表面曲线最靠近前缘的控制点方向的无量纲参数，该参数越大，对应的前缘曲率半径就越大。由响应面可以得到前缘曲率半径越大，巡航构型阻力系数越大，着陆构型升力系数越大，巡航构型上表面转捩位置越靠前。此外，响应面可以直观的反映出参数_对3个目标函数的影响性是最大的。基于ANOVA的参数影响性分析如图27所示，也反映出参数_对3个目标函数的影响性是最大的。

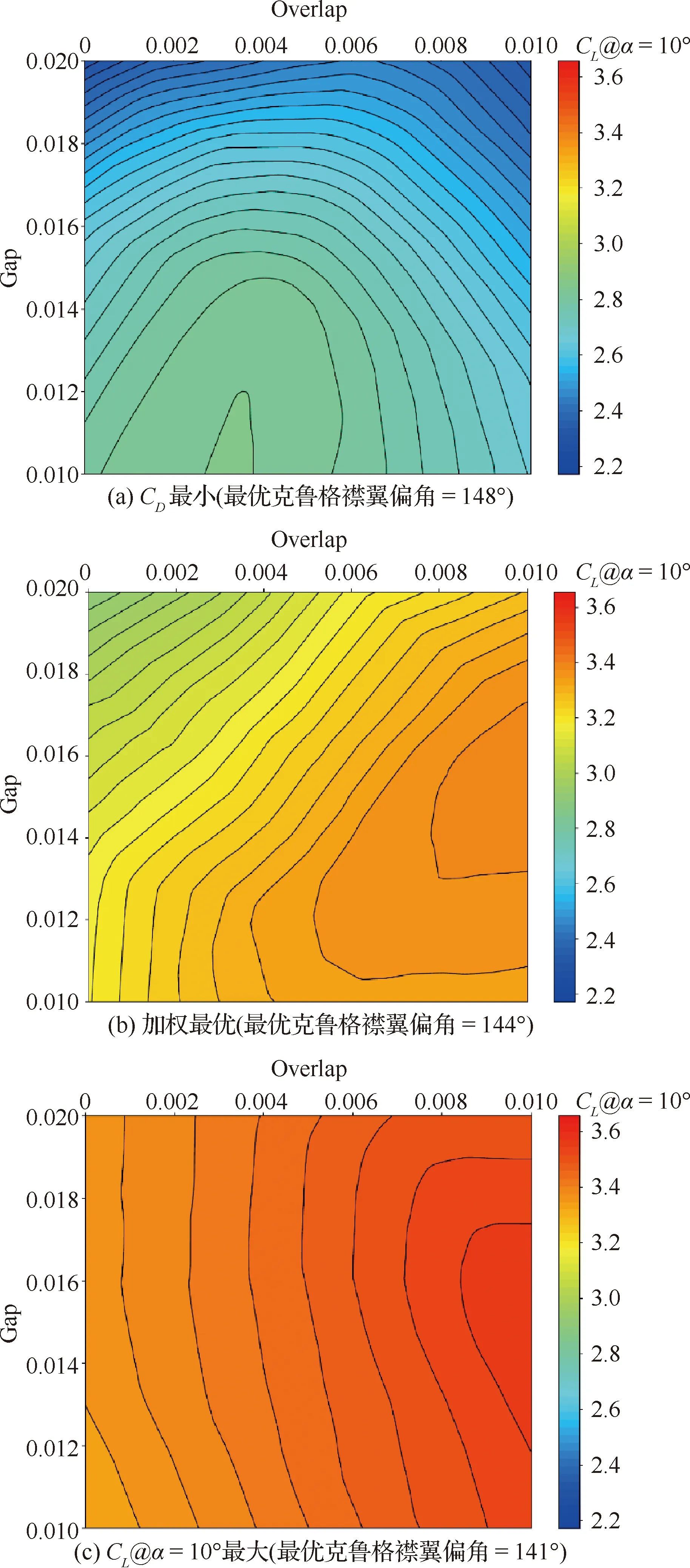
图23 嵌套协同优化3个较优点的克鲁格襟 翼缝道参数响应面Fig.23 Response surfaces of gap/overlap of Krueger flap of three optimal points of nested collaborative optimization

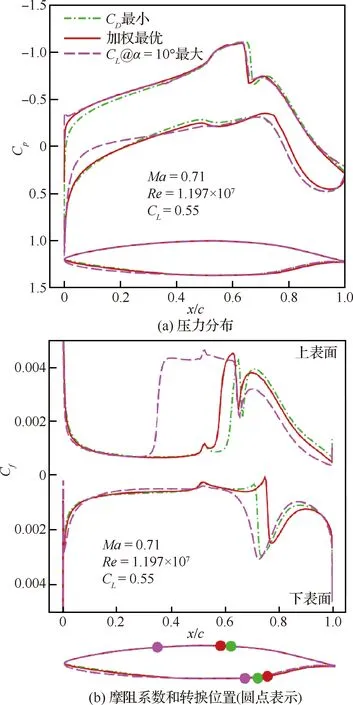
图24 嵌套协同优化3个较优点巡航构型对比Fig.24 Comparison of cruise configuration of three optimal points of nested collaborative optimization

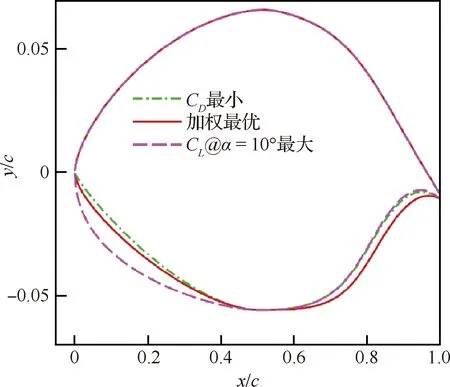
图25 嵌套协同优化3个较优点翼型对比Fig.25 Comparison of airfoils of three optimal points of nested collaborative optimization

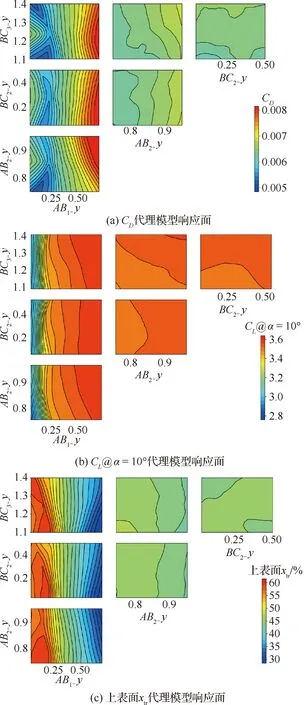
图26 代理模型响应面Fig.26 Response surfaces of surrogate models

巡航构型阻力发散特性如图28(a)所示，虽然‘最小’比‘加权最优’在0.71设计点的阻力只小了0.000 1，但是‘加权最优’的阻力发散特性恰巧是最优的。着陆构型升力曲线对比图28(b)所示，随着翼型下表面前缘曲率半径增加，克鲁格尾缘的弯度也相应的增加，从而能使它支持更大的偏角而不发生流动分离，使克鲁格上表面压力分布得到改善，由此也改善了主翼上表面的压力分布，最终使失速攻角增加，最大升力系数提升。嵌套协同优化3个较优点着陆构型压力分布对比如图29所示，失速迎角马赫云图和流线对比如图30所示，‘最小’在=8°就失速，并且后缘襟翼上表面已经有明显的流动分离，嵌套协同优化后的‘加权最优’失速迎角提升到了10°，并且还未发生明显的流动分离。

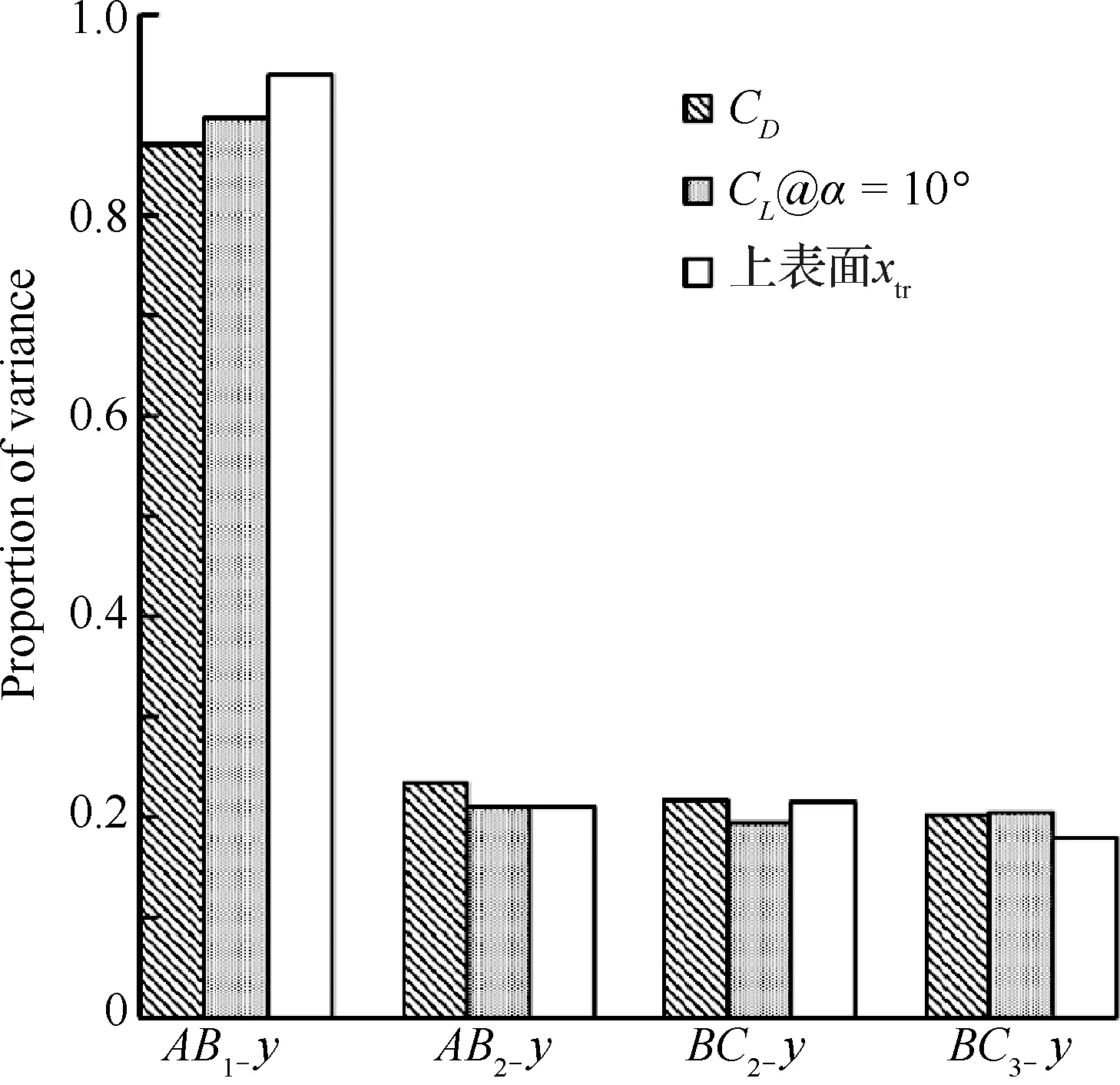
图27 翼型下表面参数对于3个目标函数影响性分析Fig.27 Influence of airfoil lower surface parameters on three objective functions

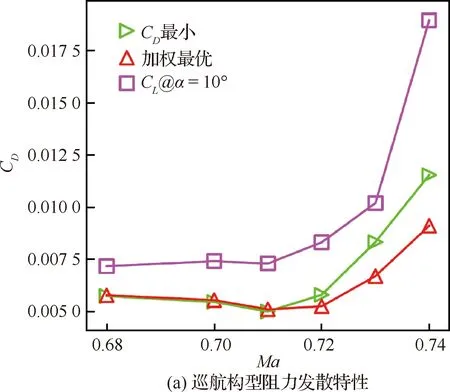
图28 嵌套协同优化3个较优点巡航和着陆构型性能对比Fig.28 Comparison of cruise and landing performance of three optimal points of nested collaborative opti-mization

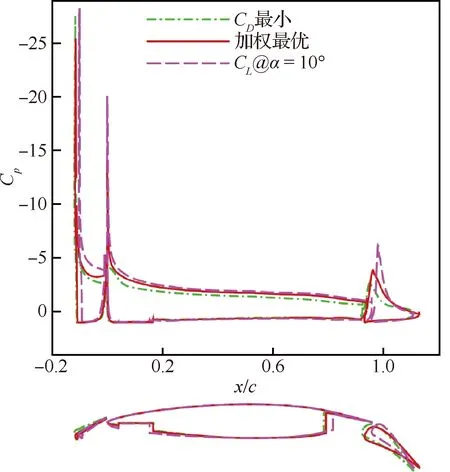
图29 嵌套协同优化3个较优点着陆构型压力分布对比Fig.29 Comparison of pressure distribution of landing configuration of three optimal points of nested collaborative optimization

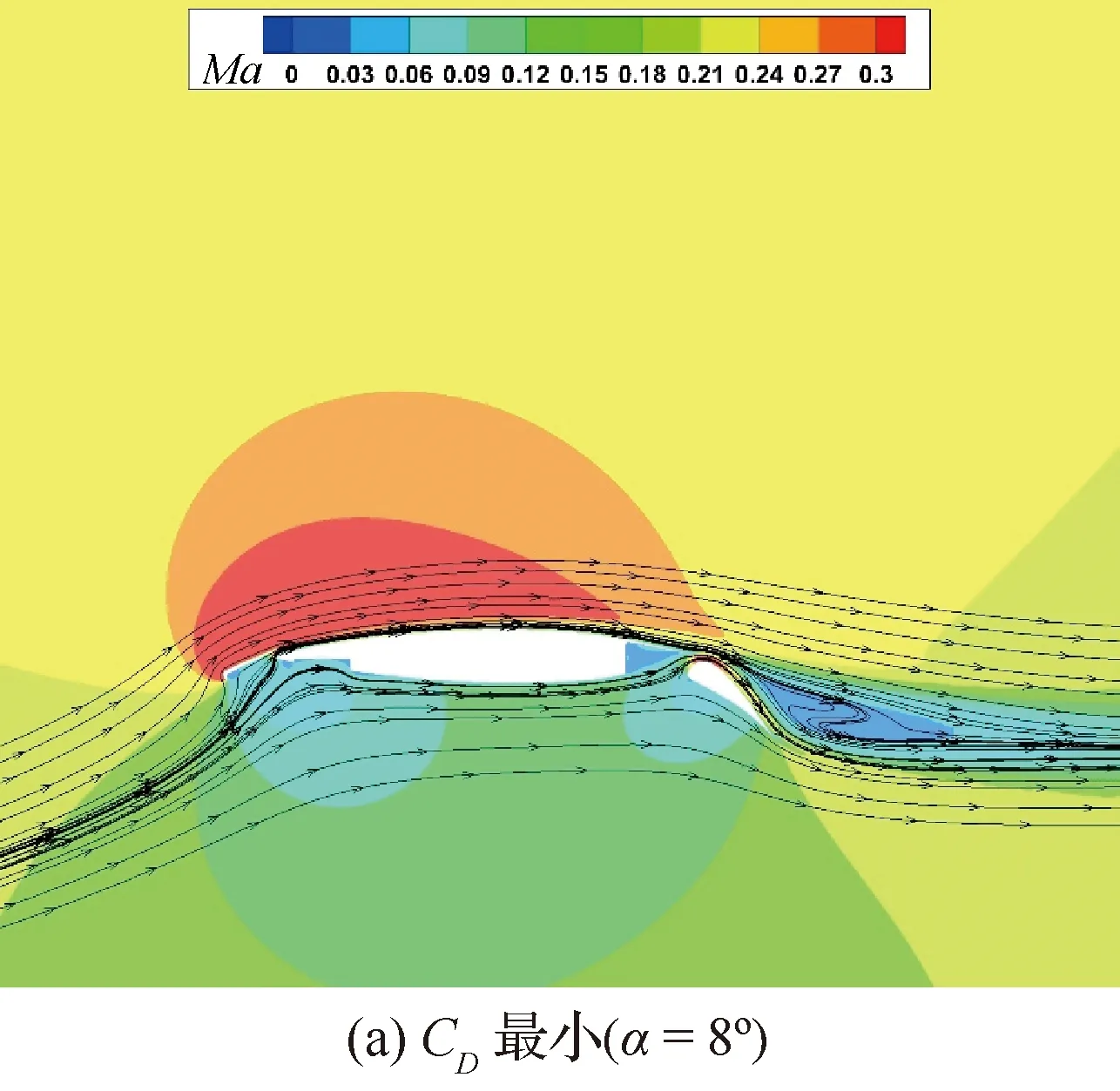
图30 嵌套协同优化3个较优点着陆构型失速迎角马赫云图和流线对比Fig.30 Comparison of Mach number contour and streamline at stall angle of attack of three optimal points of nested collaborative optimization

3 三维层流机翼和增升装置优化

本节在第2节嵌套协同优化得到层流翼型的基础上开展层流机翼及增升装置的优化。优化流程图如图31所示，首先针对层流机翼开展优化，将第2节嵌套协同优化得到的‘加权最优’翼型布置在3个截面上(翼根、翼尖和37%展长位置)得到基准机翼，然后对3个截面的翼型同时开展优化，并且约束翼型前缘曲率半径变化范围下界大于基准翼型，这样可以保证对机翼进行优化时，增升装置的性能不会变差。然后在优化的机翼上通过二维截面的优化来实现三维增升装置的优化，简单来说，首先在二维截面上开展优化设计(展向位置40%和70%处的截面)，然后使三维模型匹配二维截面的外形和缝道参数，这样可以保证优化效果的同时，大大减少计算量。

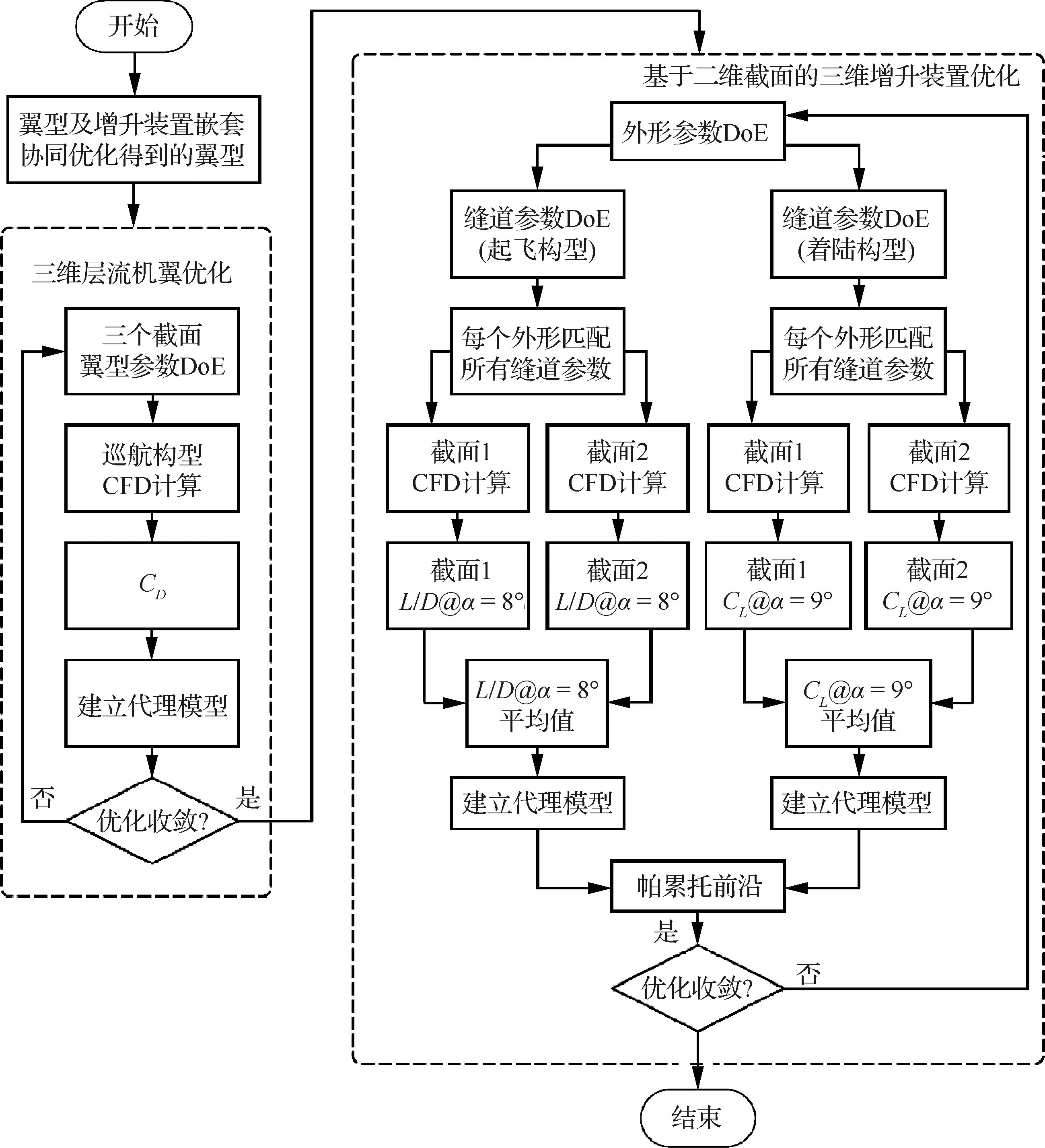
图31 三维层流机翼和增升装置优化流程图Fig.31 Flow chart of optimization of three-dimensional laminar wing and high-lift devices

三维梯形翼的平面形状参考了CRM-NLF，在表8中给出，巡航马赫数为0.75，所以前缘后掠角对应的调整为25°。基准机翼与优化机翼不同截面压力分布和转捩位置对比如图32所示，阻力系数在表9中给出，优化机翼相比基准机翼总阻力减小了3.46%，压差阻力和摩阻都有所减小。由于三维机翼有扭转角，基准机翼的3个截面直接使用二维的优化翼型后，只有外翼部分的压力分布满足要求，层流区域较大，优化后的机翼明显改善了内翼部分的压力分布，满足层流翼型的压力分布要求，从而增加了层流区域，将37%展长位置的上表面层流区域从20%提升到了40%。基准机翼与优化机翼扭转角分布对比如图33所示，优化机翼的扭转角变化范围相比基准机翼更小。

表8 CRM-NLF 模型参数Table 8 Parameters of CRM-NLF

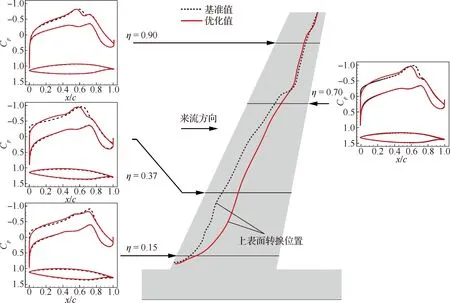
图32 基准机翼与优化机翼不同截面压力分布和转捩位置对比Fig.32 Comparison of pressure distribution and transition line between baseline and optimized wings

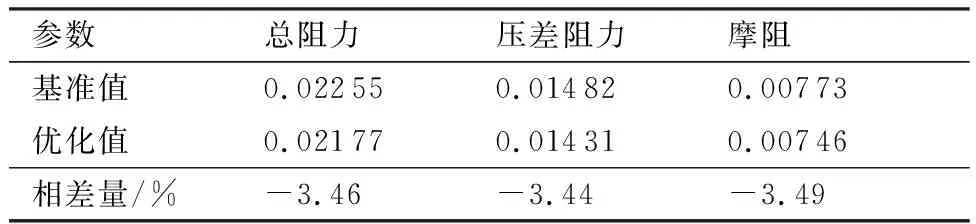
表9 基准机翼与优化机翼阻力系数对比

然后在优化的机翼上通过二维截面的优化来实现三维增升装置的优化。在两个二维截面上(展向位置40%和70%处的截面如图34所示)首先针对富勒襟翼和克鲁格襟翼外形参数生成140个样本点，针对起飞和着陆构型的缝道参数各生成120个样本点。然后对于每个外形参数样本点，匹配所有起飞和着陆构型的缝道参数样本点，这样起飞和着陆构型各得到16 800个样本点。之后分别在截面1和截面2上开展所有样本点的CFD计算，对于起飞构型计算@=8°，对于着陆构型计算@=9°。去掉不符合条件的外形后，最后总共计算量为30 000个 样本点。然后计算两个截面@=8°和@=9°的平均值，得到帕累托前沿如图35所示。最后通过对两个目标使用相同的加权系数(0.5)，得到优选的样本点，如图35中三角所示。

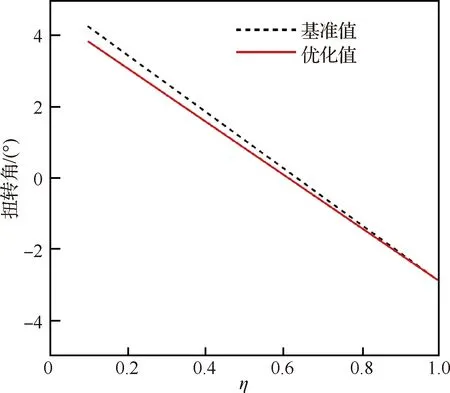
图33 基准机翼与优化机翼扭转角分布对比Fig.33 Comparison of twist distribution between baseline and optimized wings

图34 增升装置优化截面位置Fig.34 Cross section position for high-lift device optimization

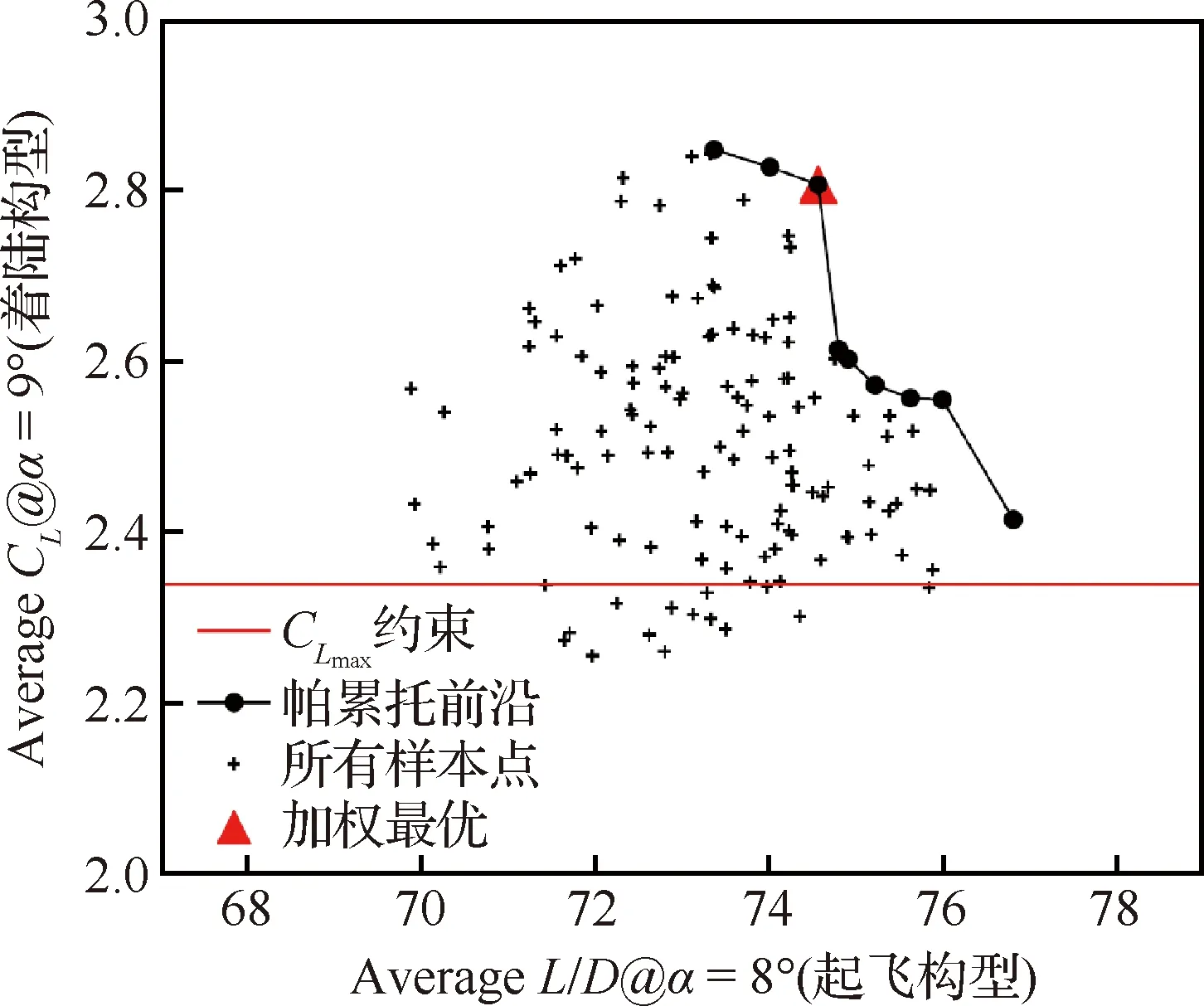
图35 两个截面二维优化得到的帕累托前沿(CL通过转换关系[9]转换成三维构型数值)Fig.35 Pareto front optimized by two sections (CL is corrected to 3D values[9])

将三维增升装置的两个截面的外形和缝道参数匹配两个截面加权最优二维构型，得到三维加权最优构型如图36所示，然后进行CFD计算，得到升力系数曲线如图37所示，压力分布对比如图38所示。三维和二维构型的失速迎角都在8°附近，三维构型和二维构型非常接近并且远超过了的约束条件，满足设计标准。三维和二

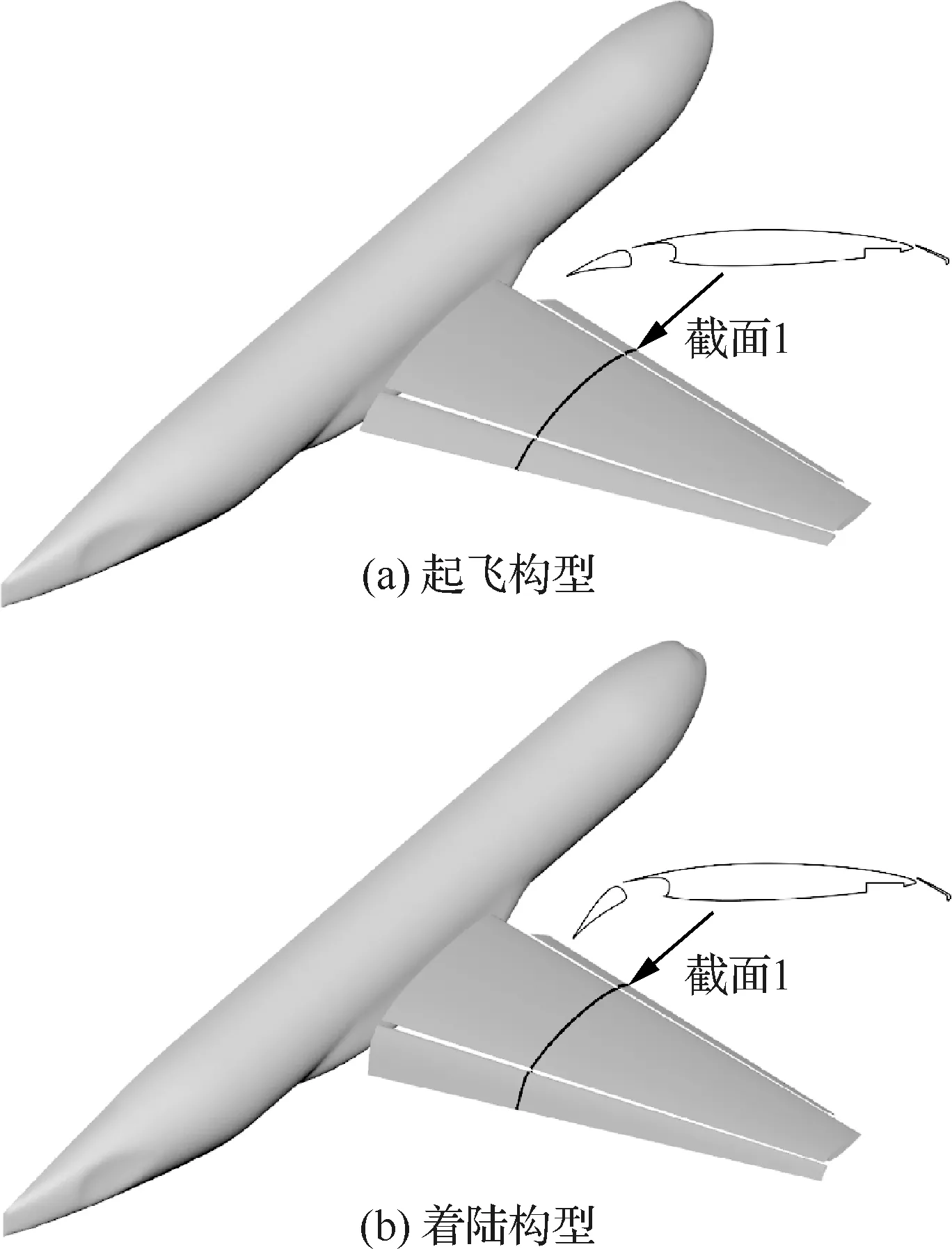
图36 匹配两个截面加权最优二维构型得到的三维加权最优构型Fig.36 3D weighted optimum configurations obtained by matching 2D weighted optimum configurations of two sections

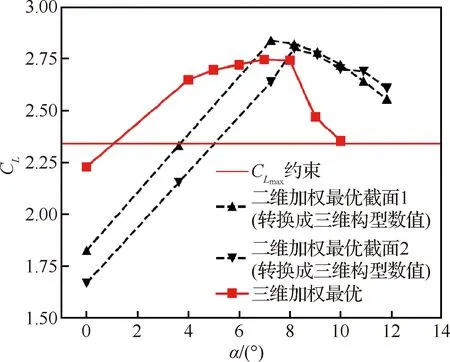
图37 三维与二维着陆构型升力系数曲线对比(二维CL通过转换关系[9]转换成三维构型数值)Fig.37 Comparison of lift coefficient curves between 3D and 2D landing configurations (2D CL is corrected to 3D values[9])

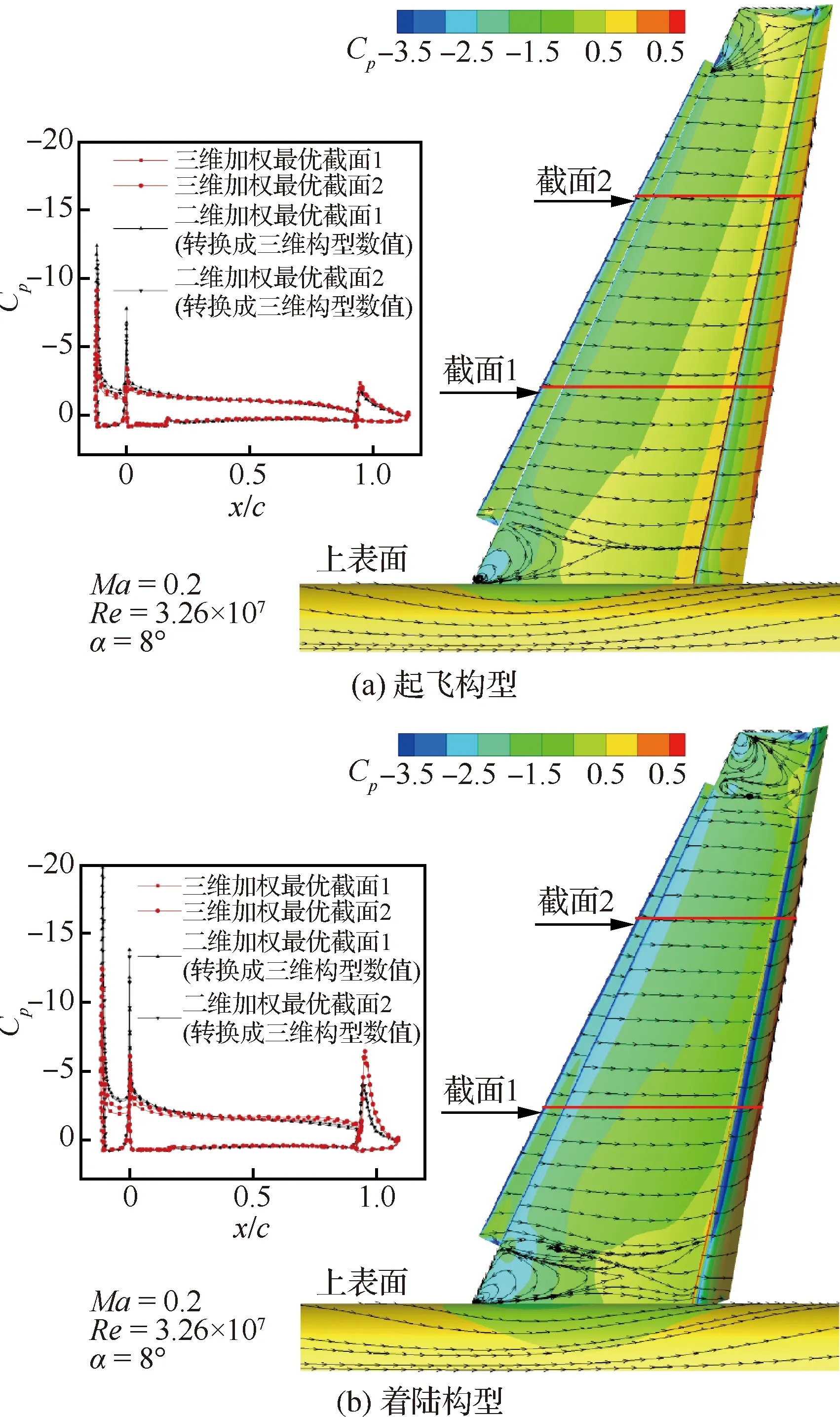
图38 三维与二维构型压力分布对比(二维Cp通过转换关系[9]转换成三维构型数值)Fig.38 Comparison of pressure distribution between 3D and 2D landing configurations (2D Cp is corrected to 3D values[9])

维构型的压力分布非常接近，说明此优化方法是有效的。对于三维构型，从表面流线可以看出有明显的三维流动，并且在翼根和翼尖有明显的流动分离，这也是与二维优化构型相比造成气动性能损失的一个原因。

4 结 论

本文在建立了层流机翼和增升装置的参数化模型的基础上，分别开展了二维翼型和多段翼型以及三维机翼和增升装置的高低速嵌套协同优化。与传统的跨声速翼型高低速协同优化通常只考虑压差阻力相比，本文的创新点在于同时考虑了跨声速层流机翼优化的两个主要目标，一是尽可能保证大范围的层流，以减小摩阻，二是减小激波强度，以减小压差阻力，由此减小总阻力，在优化高速翼型的同时考虑了低速增升装置的性能。

相比传统的先优化巡航构型，再优化缝道参数的顺序非耦合设计方法，本研究使用嵌套协同设计方法，在保证对巡航构型性能影响很小的情况下，大幅提升了着陆构型的性能。文中在二维翼型上得到的结论对三维的优化设计有参考价值，开展了基于多截面翼型的三维梯形翼优化。之后，在优化得到的层流机翼巡航构型的基础上开展了增升装置的优化设计。考虑到三维增升装置模型的参数较多，且三维CFD计算量较大，直接开展三维优化设计的计算量可能在工程上无法承受，所以通过二维截面的优化来实现三维增升装置的优化不失一种可行的选项，这样可以保证优化效果的同时，大大减少计算量。三维构型和二维构型非常接近并且远超过了的约束条件，满足设计标准。三维优化构型的截面压力分布和二维优化构型非常接近，说明此优化方法是有效的。