适用于可压缩流动的 -Re t-fRe转捩模型

刘清扬，雷娟棉，刘周，石磊，周伟江

1. 北京理工大学 宇航学院，北京 100081 2. 中国航天空气动力技术研究院，北京 100074

高超声速飞行器研制以及与之相关的高超声速空气动力学是当前研究的重点，其中高超声速边界层转捩研究具有十分迫切的工程需求。边界层转捩对高超声速飞行器的气动特性影响显著，而低冗余、一体化的高超声速飞行器设计需要较为准确的预测转捩位置和转捩区的发展，这不仅要求高超声速转捩理论的进步和实验能力的提高，同时也需要工程实用化的高超声速转捩数值预测手段。

最近的十几年里，基于局部流场变量构造，通过求解偏微分输运方程的转捩模型得到广泛的研究和应用。其中最具有代表性的是- 转捩模型，模型构造了基于间歇因子和转捩动量雷诺数 的输运方程，并通过大量实验数据分析建立的转捩区长度与临界转捩雷诺数的经验关系式，使得该模型对转捩预测有了一定的可靠性，因此被很多CFD代码和软件采用，成为当前工程研究最流行的转捩模型。

标准- 转捩模型基于低速流动发展得到，因此将- 转捩模型应用于超声速和高超声速流动时需要对模型进行修正。张毅锋等针对可压缩性和湍流普朗特数进行了修正，并成功验证了MF-1飞行试验数据。Krause、张晓东、夏陈超、Frauholz等各自发展了针对高超声速流动的关联函数。Wang等利用相似解改进了- 转捩模型在高超声速下的转捩触发判据。这些针对性的改进使得- 转捩模型的应用范围得到进一步的扩展。

除了对- 转捩模型进行适应高速流动的扩展外，针对高超声速流动的特点也发展了特有的转捩模型。王亮和符松基于非湍流脉动概念提出了适用于高超声速流动的--转捩模型。周玲等改进了--转捩模型，使之扩展到高超声速横流转捩模拟。徐家宽等构建了-转捩模型，其中是层流脉动涡黏性系数，较好地预测了由第一和第二Mack不稳定模态诱发的超声速和高超声速转捩。Shi等基于高超声速静风洞数据发展了工程转捩模型，较好地预测了HiFiRE-5外形的高超声速转捩。

这些面向超声速和高超声速流动所修正和发展的转捩模型已经取得一定的成功。与其他模型相比，- 转捩模型可以通过与试验的关联包括多种转捩效应，具有高度的灵活性和可扩展性，因而在高速转捩模拟中获得更多的应用。但高速可压缩流动转捩的实验数据比低速更为稀缺，且影响高速流动转捩的因素更多，难以从数据中获得一个相对统一的转捩准则和关联函数，已有的修正和扩展往往针对特定条件，难以适应到更广泛的情况，而且与原始低速模型不能很好的相容。

本文研究基于广泛应用的- 转捩模型，针对已有的转捩准则引入可压缩性修正，利用基于参考温度法的雷诺数可压缩性比拟关系修正现有基于不可压缩流动的转捩关联函数，并通过额外构造的输运方程避免使用全局参数，从而建立考虑流动可压缩性的- -转捩模型，以较小的计算代价实现- 转捩模型向可压缩高速流动的扩展，并具备从低速流动到高速流动的无缝统一模拟能力。

1 γ-Reθ t-fRe转捩模型发展

1.1 转捩准则的可压缩性修正

在- 转捩模型中，当流动的动量厚度雷诺数大于转捩临界雷诺数 后，转捩被触发。对不可压绝热平板边界层，边界层中涡量雷诺数和动量厚度雷诺数有如下关系：

max()=2193·

(1)

式中：和的定义为

=，=

(2)

其中：是到壁面的距离；为密度；为黏性系数；是应变率；是速度；是动量厚度；下标e代表边界层的外缘。

因此- 转捩模型的转捩触发控制函数为

=(2193 )

(3)

即当边界层内的超过2.193倍的转捩临界雷诺数 后，>1，此时转捩被触发。该条件基于不可压绝热平板边界层得到，并不适应于可压缩流动，需要修改。对可压缩平板边界层，和之间的关系随边界层外缘马赫数、温度以及壁面温度而变化。图1(a)给出了不同、相同和下可压缩平板边界层内和的关系曲线；图1(b)给出了马赫数=6时不同壁温下可压缩平板边界内的和关系曲线。图中为边界层厚度。

从图1中可见，在亚声速时，当壁温和边界层边缘温度相等，与的比值基本和不可压绝热平板的值相等；在超声速和高超声速时，与的比值要大于不可压平板的值2.193；在高马赫数下，壁温越高，2.193·和max()的偏差越大。在真实的高超声速飞行中，壁温显著高于来流温度，因此修正是必须的。对可压缩流动，边界层内和关系可以修正为

max()=·2193·

(4)

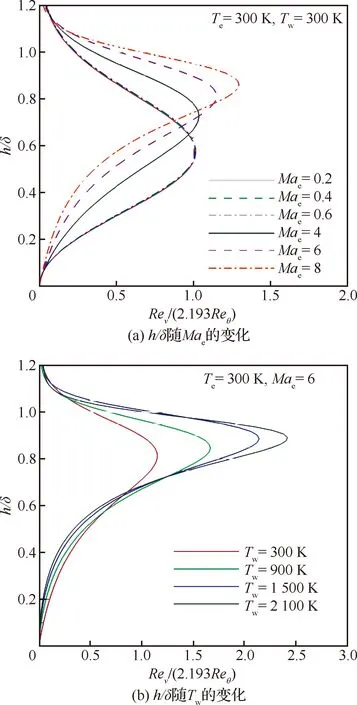
图1 可压缩平板边界层内的Rev和Reθ关系曲线Fig.1 Relations between Rev and Reθ in compressible plate boundary layer

式中：是修正函数，本文采用的表达形式为

lg()=·(lg())+

·lg()+

(5)

其中：系数、和是的函数，

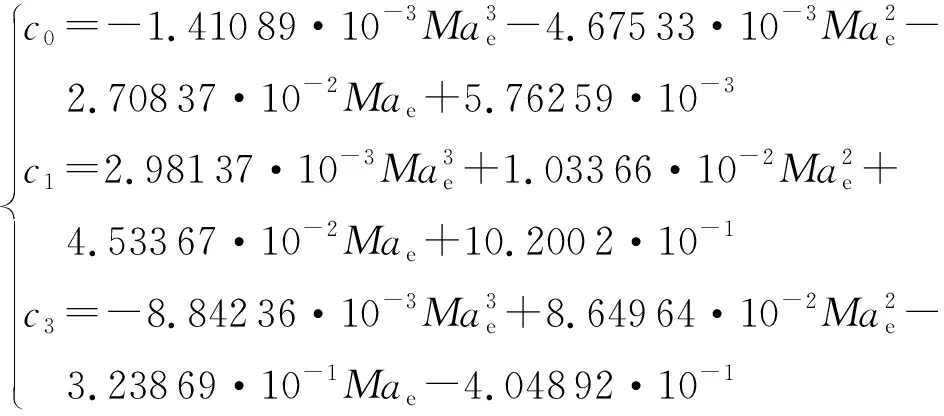
(6)

其中：=min(max(0.4,), 8)。

如图1(a)所示，当边界层边缘马赫数小于0.4 时，边界层内和关系基本不变，通过该限制确保拟合函数的取值合理。

式(5)中的是参考温度，使用Eckert用于层流超声速流动的参考温度定义：

=050×+022×+028×

(7)

式中：是绝热壁面温度，定义为

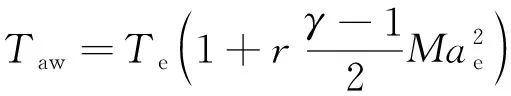
(8)

其中：是恢复因子，空气通常取0.85。对等温壁面边界，为给定值；对绝热壁面边界，=。

从修正函数的构造过程可见，该修正函数同时考虑了马赫数和壁温的影响。图2给出了不同和不同/下修正函数的曲线，从图中可见，随着变小，在/逐渐趋近于1时，的值趋近于1，恢复为不可压绝热壁面平板边界层流动的结果。而对高超声速飞行器绕流，/通常在2～5之间，此时修正函数的值在1.5～2.5之间。

图2 不同Mae下修正函数Cfc随Tw/Te的变化Fig.2 Curves of Cfc vs Tw/Te with different Mae

在获得修正函数后，需要将其应用至转捩判断中。一种直接的思路就是在式(3)的分母上乘以的值，然而的计算需要用到边界层外缘的和，获得这些值对于当前基于非结构网格的并行CFD代码是十分困难的。

结合- 转捩模型的构造思想，的值并不显式的应用于式(3)的触发判断，而是通过修改转捩雷诺数 来实现。- 转捩模型原始采用基于实验的转捩准则和基于湍流度和压力梯度参数的函数，可表示为

=()·()

(9)

针对可压缩流动，应用修正函数，式(9)被修改为

=()·()·

(10)

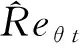
通过对转捩准则 加入可压缩性修正，基于不可压流动的转捩准则被直接扩展到可压缩流动，后续的算例计算表明这样的扩展是合理的。

1.2 雷诺数可压缩性比拟关系fRe输运方程

在基本- 转捩模型应用于高超声速转捩的模拟中，一个常见的问题是计算得到的转捩区发展太慢，这表明间歇因子方程中的生成源项太小。一种解决方式是修改关联函数以和实验结果匹配，但这种方法不具备普适性，仅适用于要求的流动条件。

参考温度法是平板可压缩流动和不可压缩流动之间的桥梁。通过参考温度法，可压缩层流平板摩阻和热流可以和不可压缩层流平板摩阻和热流联系在一起，两者之间的动量厚度雷诺数也有相应的比拟关系：

(11)

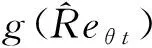
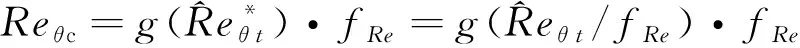
(12)

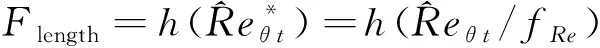
(13)

图3给出了=300 K时不同/下的曲线。从图中可见，对实际高超声速飞行器绕流，的值大约在4～16之间；而对不可压流动，的值恢复为1，关联函数恢复为原始形式。

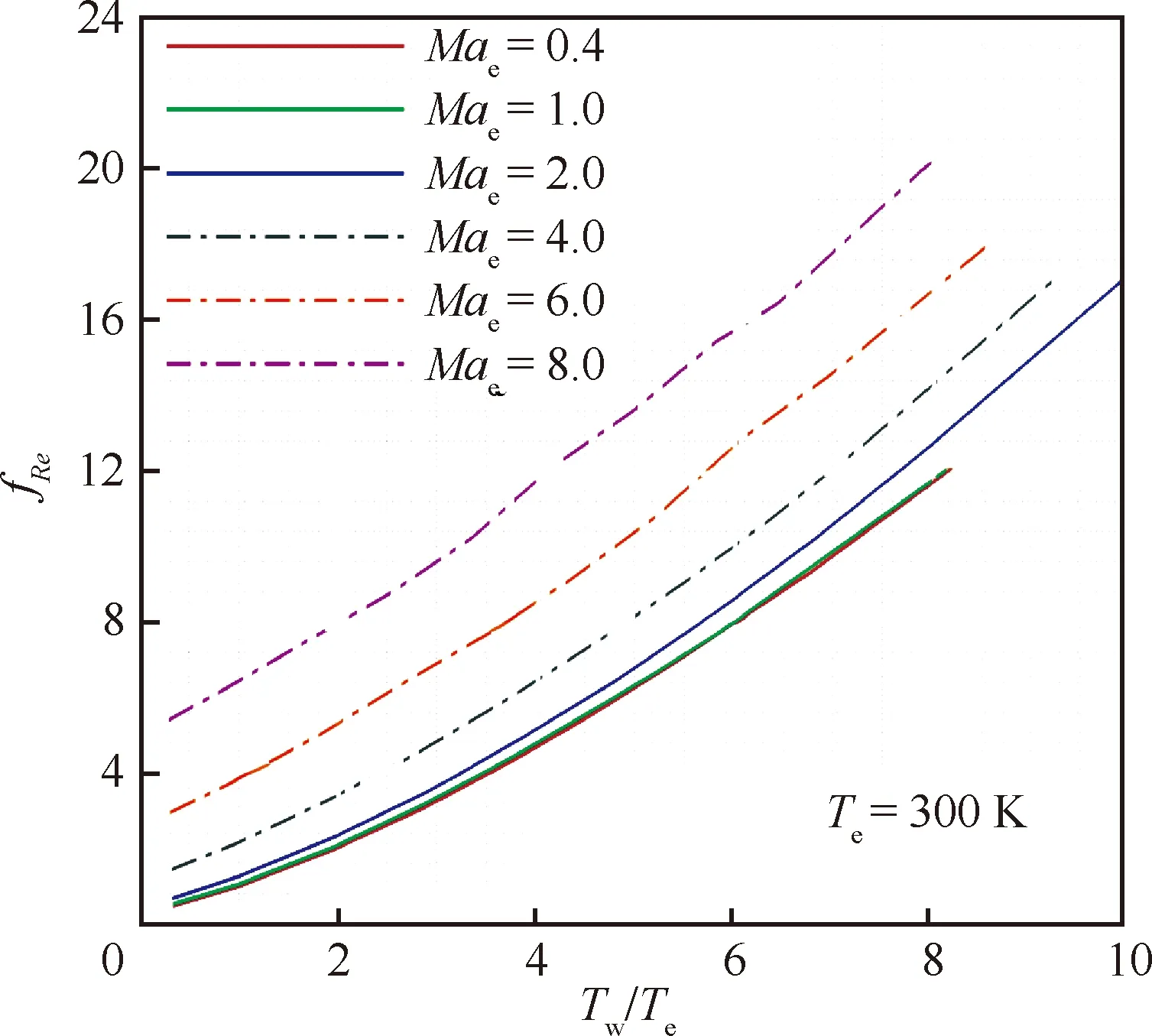
图3 不同Mae下雷诺数比拟关系fRe随Tw/Te的变化Fig.3 Relations of Reynolds number relation fRe and Tw/Te with different Mae

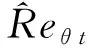
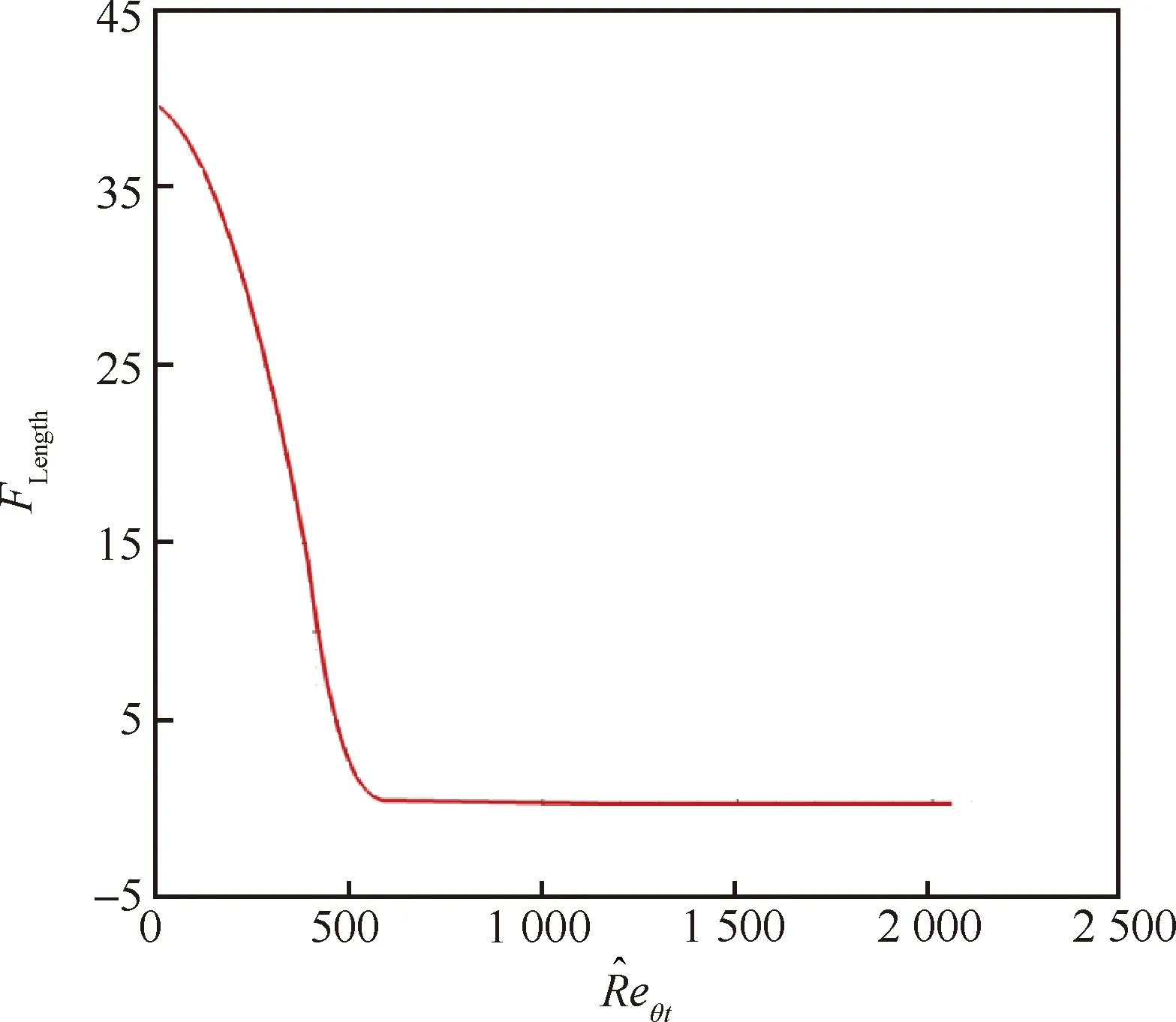
图4 关联函数Flength随变化的曲线Fig.4 Curve of Flength changing with

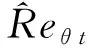
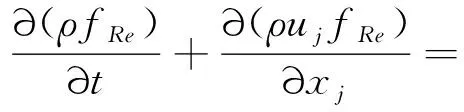
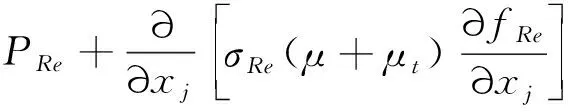
(14)

源项的表达式为

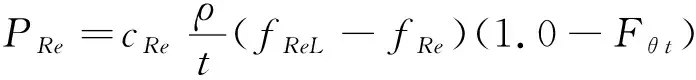
(15)

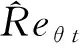
从式(15)可见，在边界层内部，源项为0，因此边界层内部的均由边界层边缘的值输运进入，采用当地流动变量获得的不会对真实的造成影响。

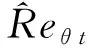
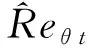
基本- 转捩模型的 定义为

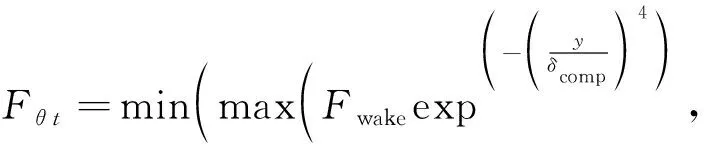
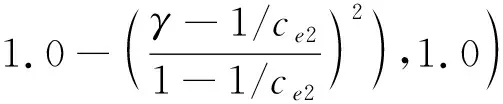
(16)

式中：是到壁面的距离；是计算获得的边界层厚度；函数用于确保 函数不会在尾迹区被激活。相关函数定义和参数的值可见文献[4]。式中()的计算是 成功的关键。基本- 转捩模型采用如下方式计算：

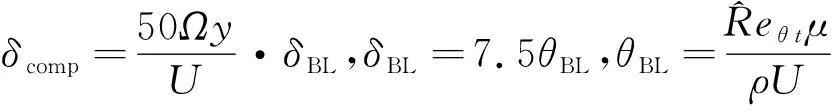
(17)

式中：是涡量。从基本- 转捩模型所用到的定义来看，边界层外缘的厚度是通过不可压平板边界层的理论解近似获得，对于可压缩边界层，这些函数关系需要修正。

虽然可以构造一个更复杂的函数来修正上述关系，但实践发现，将原始定义中的=7.5简单修正为

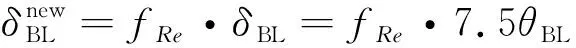
(18)

即可很好地改善可压缩流动时边界层内外的判断。

图5给出了=8、=300 K、=1 500 K，采用不同边界层内外判断定义时平板层流的()值的比较。从图中可见，修正的定义更

图5 不同δBL定义获得的平板层流(y/δcomp)4Fig.5 (y/δcomp)4 of laminar flow on plate with different δBL

保守，与原始定义相比，修正的定义确保了在边界层内()=0，从而使得 =1。

至此，通过额外的输运方程，将基本- 转捩模型扩展为可压缩- -转捩模型，使之可用于超声速和高超声速转捩的模拟；不可压缩流动时比拟关系退化为1，可压缩- -转捩模型自然恢复为基本- 转捩模型，从而实现了从不可压低速流动至可压缩高速流动的统一转捩计算。

1.3 初始条件和壁面边界条件

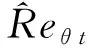
和基本- 转捩模型一样，- -转捩模型中的3个输运方程在壁面处的法向通量为0。

2 γ-Reθ t-fRe转捩模型验证

2.1 低速平板转捩流动

- -转捩模型在低速不可压时会恢复为基本的- 转捩模型。本节针对不同低速平板转捩流动，验证- -转捩模型与基本- 转捩模型的兼容性。

表1给出了所采用的零压力梯度平板流动的计算条件，其中下标inlet表示距平板前缘0.04 m入口处的值。图6给出了不同模型计算得到的摩阻系数和实验的对比，其中湍流结果采用SST湍流模型计算得到。

表1 低速平板转捩流动计算条件[4]Table 1 Transition flow conditions for low speed plate[4]

从图6中可见，对于不可压低速流动条件，- -模型的结果和基本- 模型的结果几乎完全一致，而且和实验吻合得相当好，这表明在低速流动条件下，- -模型自动恢复为基本- 模型，两者在低速是完全兼容的。这同时也表明，在式(6)中采用0.4作为的下限进行截断是恰当的。

图6 低速平板转捩流动的计算摩阻和实验对比Fig.6 Friction for low speed plate transition from computation and experiment

转捩模拟没有很好地获得T3A平板在转捩结束时的过冲现象，这可能和当前采用的基本湍流模型有关。本文与- 转捩模型进行耦合的是两方程SST湍流模型，文献[24]将- 转捩模型与雷诺应力湍流模型进行耦合，较好地模拟了T3A平板在转捩结束处的过冲现象。

2.2 高超声速平板转捩流动

高超声速平板转捩流动对应的实验是Mee在激波风洞中进行的，本文选取的计算条件见表2，其中下标inlet表示距平板前缘0.04 m入口处的值。壁面边界条件为等温壁，壁温=300 K。

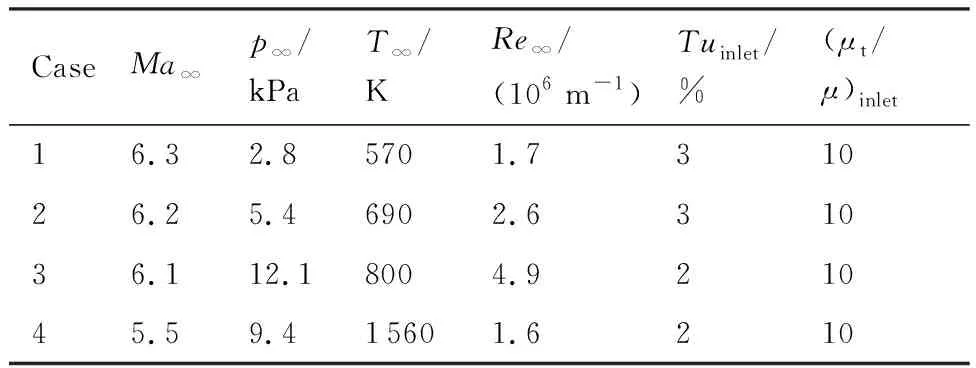
表2 高超声速平板流动条件Table 2 Flow conditions for hypersonic speed plate

计算网格约13万网格单元，为确保收敛和正确地捕获转捩位置，壁面均小于1。图7给出了不同条件下计算获得的壁面Stanton数分布和实验的比较。在该例中Stanton数定义为

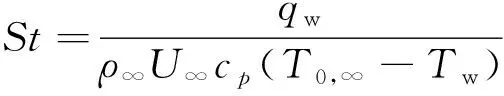
(19)

从图7中可见，4种来流条件下，- -模型获得的热流分布和实验吻合得相当好，而基本- 模型获得的转捩区过长。特别对于高焓条件的Case 4，基本- 模型未能给出明显的转捩，而- -模型正确地捕获了转捩。总体而言，- -模型有效改善了高超声速平板转捩流动的模拟。

2.3 半锥角5°尖锥Ma=3.5超声速转捩流动

半锥角为5°的尖锥计算条件取自文献[26-27]等在低扰动风洞的试验，具体条件见表3。从表中可见，通过调整来流压力，可以研究不同雷诺数下的尖锥转捩特性。

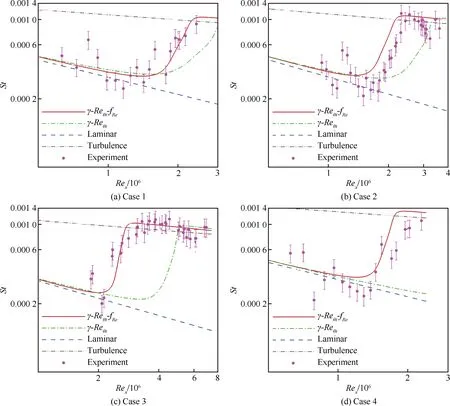
图7 高超声速平板转捩Stanton数Fig.7 Stanton number for hypersonic plate transition

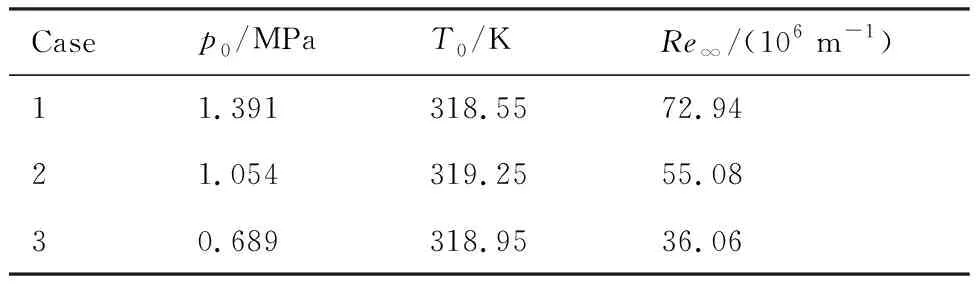
表3 半锥角5°尖锥Ma=3.5来流条件

试验数据是从低扰动风洞中获得的，故计算时来流湍流度取为0.1%，来流/=10，壁面边界条件为绝热壁面边界。

由于迎角为0°，计算域为1/4锥。计算网格是六面体网格，共约400万网格单元，流向221个网格点，其中181个点在锥体表面，法向301个网格点，如图8所示。

图8 半锥角5°尖锥计算网格Fig.8 Computational grid for 5° half angle sharp cone

实验采用的是绝热壁面，转捩的影响通过恢复因子分布体现。恢复因子定义为

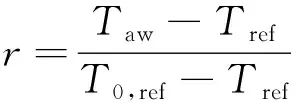
(20)

式中:为参考温度，是过激波之后的流场温度;是过激波之后的总温;是实验或计算得到的壁面温度。

图9给出了计算得到的恢复因子和实验的比较。从图中可见，基本- 模型和- -模型都计算出了转捩，基本- 模型得到的转捩位置更靠前，而- -模型的转捩位置和转捩区发展与实验吻合得更好，不同来流条件下的转捩雷诺数都约为7.5×10。此外基本模型在转捩前恢复因子有一个非物理的下降过程，文献[9，28]中也报道过类似的情况；而- -模型的恢复因子在转捩前一直保持层流结果，没有非物理的下降。

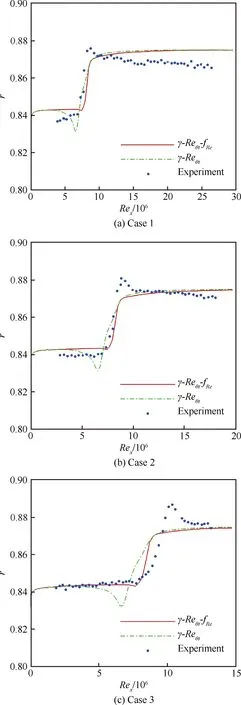
图9 恢复因子沿尖锥表面的分布Fig.9 Distribution of recovery factors along cone surface

实验结果在湍流区的恢复因子有一个较尖锐的峰值，然后沿流向逐步缓慢下降，计算没有观察到这样的现象，文献[9]认为采用变湍流Prandtl数的湍流模型可能会改善计算结果。

半锥角5°尖锥=3.5的超声速流动转捩模拟表明，相比于基本- 模型，- -模型明显改善了转捩模拟结果。

2.4 半锥角5°尖锥Ma=6.0高超声速转捩流动

选取Horvath等在=6常规风洞中针对半锥角5°尖锥的高超声速流动转捩试验，用于计算的来流条件见表4。

表4 半锥角5°尖锥Ma=6.0来流条件

计算网格参见图8。计算采用等温壁，所有计算的壁温=0.59。在计算中入口湍流度=3.0%，入口处的(/)=16，下标inlet表示距尖锥顶点0.01 m入口处的值。

图10给出了不同模型计算得到的无量纲传热系数和实验的对比。这里=/(-)，为壁面热流，为焓，为由Fay-Riddell驻点热流公式给出的参考值。

从图10中可见，本文所发展的- -模型较好地捕获了转捩，在不同雷诺数下转捩起始位置和转捩区的发展都和实验吻合得相当好。对于Case 1和Case 2，试验的无量纲传热系数存在明显的峰值，而计算中没有获得类似的结果，这个现象和2.3节中=3.5的5°半锥角尖锥的结果类似，有可能和湍流模型对可压缩流动的适应性相关。

图10 传热系数沿尖锥表面的分布Fig.10 Distribution of heat transfer coefficients along cone surface

图10中的Case 1和Case 4也给出了基本- 模型、层流和全湍流的结果。从图中可见，基本- 模型预测的转捩位置更靠前，但转捩区的强度远小于- -模型，转捩区长度更长。这是因为基本- 模型的转捩准则缺乏可压缩性修正，使得转捩位置提前；同时基本- 模型用于间歇因子γ方程的F过小，使得方程的生成源项太小，产生了不正确的转捩发展。总体而言，相比于基本- 模型，- -模型有效改善了半锥角5°尖锥=6.0的高超声速流动转捩模拟精度。

3 结 论

通过一系列不同流动条件的转捩算例对本文所发展的- -转捩模型进行了考核检验，计算结果表明：

1) 在低速流动条件下，- -模型自动恢复为基本- 模型，两者的结果几乎完全一致。

2) 针对转捩准则的可压缩性修正改善了超声速和高超声速流动的转捩起始位置预测。

3) 利用雷诺数比拟关系对关联函数的修正改善了可压缩流动转捩区发展的预测。

4)- -模型将基本的- 模型扩展到可压缩流动，实现了从低速至高速的无缝统一模拟能力。