一些曲面测地线方程的几种计算方法
2022-09-06肖曼玉
马 荣, 马 骏, 肖曼玉
(西北工业大学数学与统计学院,西安 710072)
1 引 言
2018年全国大学生数学竞赛数学类三、四年级组微分几何选考题目[1]:已知椭圆柱面S∶r(u,v)=(acosu,bsinu,v),-π≤u≤π,-∞
首先给出测地曲率定义.
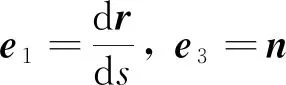
Dv=(df1+f2ω21)e1+(df2+f1ω12)e2,
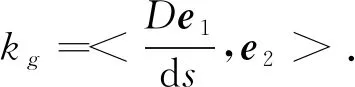
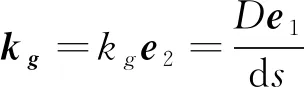
(1)
对于r求二阶混合偏导有

由于测地曲率是曲线自身在曲面内的弯曲程度,故应只考虑rγ和rα,即测地曲率向量为
下面给出测地线定义及其所满足的方程组.
定义2[2]曲面上测地曲率等于0的曲线称为曲面的测地线.
由此定义,显然可知当曲面的参数表示为r=r(u1,u2)时,测地线应满足方程:
以下解决“已知椭圆柱面S∶r(u,v)=(acosu,bsinu,v),-π≤u≤π,-∞ 首先给出曲面S的切向量ru和rv,ru=(-asinu,bcosu,0),rv=(0,0,1). 另外给出曲面S的单位法向量[1] (2) 设γ是S上的任意测地线,其参数方程设为u=u(t),v=v(t),t∈.由于任意曲面上的直线(若存在)都是测地线,从而S上的直母线(u≡常数)为测地线,于是,只需求u′(t)≠0的测地线,作γ的参数变换使得它以显式函数v=f(u),u∈[-π,π]来表示,所以,测地线γ的向量式参数方程为 r(u)=(acosu,bsinu,f(u)),u∈[-π,π]. 对参数u分别求一阶导和二阶导,可得 r′(u)=(-asinu,bcosu,f′(u)), r″(u)=(-acosu,-bsinu,f″(u)), (3) 则γ的单位切向量为 T(u)=|r′(u)|-1r′(u). (4) 因此,曲线γ在曲面S上的测地曲率为 所以,γ是测地线当且仅当(r″,n,T)=0从而由(2),(3),(4)式可得 (5) 此式等价于 f″(a2sin2u+b2cos2u)=f′(a2-b2)sinucosu. (6) (i) 若f′=0,则v=f(u)≡常数,曲线γ是S上的正截线,即椭圆; (ii) 若f′≠0,则(6)式等价于微分方程 再进行积分可得 (7) 所以S上的测地线为如下三类曲线, (a)S上的直母线(v≡常数); (b)S上的横截椭圆(u≡常数); (c) 曲线由(7)式确定. 受到该问题的求解方法启发,下面针对旋转轴为z轴,母线Γ的参数方程为(φ1(t),φ2(t),φ3(t)),a≤t≤b的旋转曲面.以下给出该旋转曲面的测地线方程. 则可以将旋转曲面记为 其中-∞ 和 其中φ′i,i=1,2,3表示φi关于u求导,从而S的单位法向量为 仍然假设γ是S上的任意测地线,其参数方程设为 u=u(t),v=v(t),t∈. 同样地,由于任意曲面上的直线(若存在)都是测地线,从而S上的直母线(u≡const)为测地线,于是只需求u′(t)≠0的测地线,作γ的参数变换使得它以显式函数v=ω(u),-∞ r′(u)=(A1(ω,ω′,φ,φ′),B1(ω,ω′,φ,φ′),φ′3), 其中 C1(ω,ω′,φ,φ′)=-cosω(φ′)2-sinω(3φφ′ω′+2φ2ω″)-2cosω(φ2(ω′)2-φφ″), D1(ω,ω′,φ,φ′)=-sinω(φ′)2+cosω(3φφ′ω′+2φ2ω″)-2sinω(φ2(ω′)2-φφ″). 由2.1节可知,γ是测地线当且仅当(r″,n,T)=0,从而可得 由此微分方程可以确定v=ω(u),从而可以给出旋转曲面测地线的方程. 由于二次曲面F(x,y,z)=0可以通过转轴变换消去交叉项,所以二次曲面的标准方程可以写为F1(x,y)+F2(z)=0,那么设F1(x,y)=α(k)[5],其中k为参数,由二次曲面标准方程有F2(z)+α(k)=0,则有 其中u,v为参数从而可以得到 则可将旋转曲面记为 S∶r(u,v)=(f1(u,f3(v)),f2(u,f3(v)),f4(v)). 其中u,v为参数.此时计算其切向量,有 仍令v=ω(u),测地线γ的向量式参数方程化为 r(u)=(f1(u,f3(ω(u))),f2(u,f3(ω(u))),f4(ω(u))). 可以计算得到 其中 仍然利用γ是测地线当且仅当(r″,n,T)=0,从而可得 由此微分方程可以确定v=ω(u),从而可以给出二次曲面测地线的方程. 定理1(Liouville定理)[2]设(u,v)是曲面S的正交参数,I=Edudu+Gdvdv,C∶u=u(s),v=v(s)是曲面上一条弧长参数曲线,设C与u线的夹角为θ,则C的测地曲率为 那么利用该公式和正交参数的性质,可得测地线的微分方程组[2]为 对于椭圆柱面,消去参数θ,并将第一基本量E=1,G=a2sin2u+b2cos2u代入可得 (8) 首先利用(8)式解出θ和u关系 (9) 将(9)式代入(8)式可以解出v和u关系, 从而可以解得椭圆柱面的测地线方程. 设二次曲面S由隐式方程F(x,y,z)=0确定,Γ∶r=r(s)是曲面S的一条曲线,由于曲线Γ在点P(x,y,z)的测地曲率 其中 于是曲面S上的曲线Γ在点P的测地曲率为 也就是说由隐式方程F(x,y,z)=0确定的曲面上的测地线的微分方程 (d2yFz-d2zFy)dx+(d2zFx-d2xFz)dy+(d2xFy-d2yFx)dz=0. 若曲面S可以由方程z=f(x,y)给出,那么可以给出测地线微分方程为 事实上,该方法的推导并未用到二次曲面的信息,也即是说该方程对任意正则曲面都成立. 利用此定理将原问题转化为求泛函 最小化时对应的曲线方程.利用Euler-Lagrange方程则有[3] 即 积分前两式可得 (10) (11) (12) 将(12)式代入(10)式有 可得 从而得到以弧长为参数的测地线方程 其中c,d,e,f均为积分常数,由起始点和终止点两点的坐标确定. (13) 由(13)式以及隐函数定理知 从而有 (14) 利用关系ds2=dx2+dy2+dz2.则有 比较系数知 解得 (15) 将(15)式代入(14)式可知 从而可以确定 其中s为弧长参数,c1,c2,c3,c4,c5均为积分常数[7].事实上,该方法的推导并未用到二次曲面的信息,同2.3节相同,该测地线方程对任意正则曲面都成立. 将椭圆柱面[1]沿其中一条直母线剪开后展为平面上的一个无限长带形区域:s1 可得 (a) 若A=0,则有v≡常数.对应椭圆柱面上的横截椭圆; 由于使用该曲面展开法需要找到和平面的等距对应,可展曲面在局部上可以和平面建立保长对应,从而利用该方法来解决可展区面的测地线问题.容易知道一个曲面是可展曲面的充分必要条件是它的高斯曲率为0. 可展曲面分三类:柱面、锥面和切线面[2]. 下面针对这三种曲面各给出一个求其上的测地线的例子. 例1仍将双曲柱面沿一条直母线剪开后展为平面上的一个带形区域: s1 As+Bv+c=0. 另一方面 故得 所以,已知椭圆柱面上所求的测地线方程为 其中A,B不全为0,从而S上的测地线为如下三类曲线: (a) 若A=0,则有v≡常数.对应双曲柱面上的双曲线; 例2同例1的方法,将二次锥面沿一条直母线剪开后展为平面上的一个扇形区域,可将该区域用延拓成一个带形区域:s1 r(u)=(acosu,bsinu,0), -π 的弧长函数,可以求得测地线方程为 A,B,C的讨论类似4.1节椭圆柱面的展开. 例3对于圆柱螺线r(t)=(acost,asint,bt),t为参数,并以k0和τ0表示其曲率与挠率,则其以弧长为参数的曲线方程为 其中s为弧长参数,根据切线面的定义r(s,t)=r(s)+tr′(s),其中t为参数,则可知 下同例1的方法,将该圆柱螺线的切线面展开成一个带形区域s1 本文由一道大学生数学竞赛题出发,通过对题目的分析,运用四种方法求解椭圆柱面的测地线问题,并由此推广到旋转曲面、二次曲面或可展曲面的测地线求解,这四种方法各有特点和优劣,因此对于不同问题选用不同的方法是非常有必要的. 例如参数变换法将v看作f(u),导出微分方程[8],它能够给出具体的曲面分类, 比较清楚和直观.另外它可以给出旋转曲面和二次曲面的一般方法,通用性较强.微分方程法利用Liouville公式导出测地线微分方程组,它不容易给出具体的曲面分类,不够直观,但是相对来说表述较为简洁,它也可以给出旋转曲面、二次曲面和一般正则曲面的一般求解测地线方程方法,通用性也较强.变分法利用测地线的极小性质考虑变分问题,借助Lagrange乘子法得到欧拉方程,引入弧长参数同样可以给出测地线微分方程,类似于微分方程法,它不容易给出具体的曲面分类,它可以给出一般曲面求解测地线方程方法,通用性同样较强.曲面展开法利用等距对应将曲面上的问题转化为平面问题,方法简单巧妙,形象直观.但是该方法需要找到可展曲面才能使用,通用性不够强. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.2 参数变换法
2.1 求解椭圆柱面问题
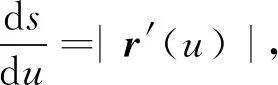

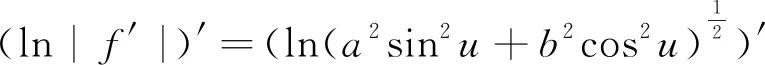
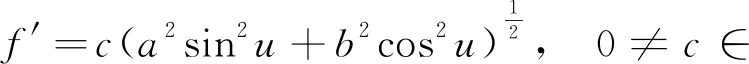

2.2 求解旋转曲面问题

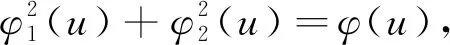
2.3 求解二次曲面问题
3 微分方程法
3.1 求解椭圆柱面问题[3]

3.2 求解二次曲面问题
4 变分法
4.1 求解椭圆柱面问题
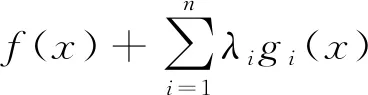
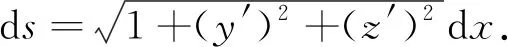
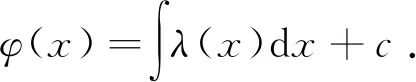
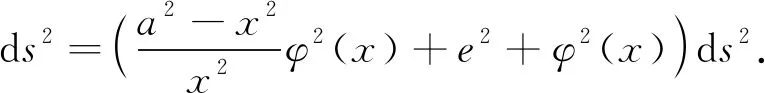
4.2 求解二次曲面问题

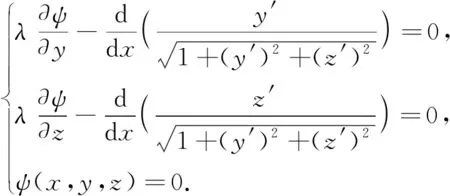
5 曲面展开法
5.1 求解椭圆柱面问题

5.2 求解可展曲面问题

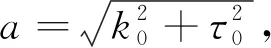
6 结 论
